碳纤维增强地聚物混凝土韧性评价指标的对比研究
朱靖塞, 许金余,2, 罗 鑫, 李为民, 白二雷, 高志刚
(1.空军工程大学机场建筑工程系,陕西西安710038;2.西北工业大学力学与土木建筑学院,陕西西安710072;3.广州军区空军后勤部机场处,广东广州510052)
碳纤维[1]是伴随着军工事业的发展而成长起来的新型材料,具有高比强度、高比模量、耐高温、耐腐蚀等一系列优异性能.与其他合成纤维相比较,碳纤维在混凝土中不仅可约束微裂纹的扩展,提高混凝土的抗裂性,而且可以提高结构的抗震性和抗疲劳特性.因此,碳纤维增强水泥基材料[2-3]的研究在国内外掀起了热潮.
地聚物[4]是一种由碱激发硅铝质材料所形成的新型胶凝材料,由于具有特殊的无机缩聚三维氧化物网络结构,使得它在众多方面具有比碱矿渣水泥、陶瓷、硅酸盐水泥等更好的性能[5].但地聚物混凝土(geopolymeric concrete,GC)仍属于准脆性材料,韧性不足,而纤维强韧化技术是目前解决此类问题的重要手段,基于此,碳纤维增强地聚物混凝土(CFRGC)应运而生.掺加碳纤维的主要目的在于提高地聚物混凝土的韧性,因此与CFRGC韧性相关的研究显得尤为重要.
近10几年来,ACI 544委员会、JCI SFRC委员会等组织相继提出不同的纤维增强混凝土韧性评价指标,这些方法[6]没有统一标准,针对具体的材料,各评价指标各有优劣,而关于CFRGC冲击韧性评价指标方面的研究成果相对少见,亟待开展相关试验和理论研究.本文首先配制了基体强度等级为C30,碳纤维体积分数φcf分别为0%,0.1%,0.2%,0.3%的CFRGC,然后采用φ100分离式霍普金森压杆(SHPB)试验装置对其开展了多个应变率范围的冲击压缩试验,基于峰值韧度和比能量吸收2种评价指标研究了CFRGC的冲击韧性,并进行了对比分析和机理探究.
1 试验
1.1 基本情况
原材料:水淬高炉矿渣(比表面积为491.6m2/kg,28d活性指数≥95%);一级粉煤灰;石灰岩碎石(5~10mm约15%1))本文所涉及的含量、纯度等除特别说明外均为质量分数.;10~20mm约85%);中砂(细度模数为2.8);化学纯NaOH片状固体(纯度≥97%);液体硅酸钠(即水玻璃,模数为3.1~3.4,SiO2含量≥26.0%,Na2O含量≥8.2%);沥青基短切碳纤维,其具体物理与力学性能指标见表1.
配合比设计:基体配合比经过试配得到,与普通硅酸盐水泥混凝土配合比设计中的重要参数水灰比类似,定义水与矿渣和粉煤灰的质量比为水胶比,具体配合比参数如下:水胶比0.31,矿渣300kg/m3,粉煤灰100kg/m3,砂629kg/m3,石子968kg/m3,液体硅酸钠和氢氧化钠的质量比为4.2.在基体GC中分别掺入体积分数为0%,0.1%,0.2%,0.3%的碳纤维.为便于分析,分别以GC,1CG,2CG,3CG表示.表2列出了CFRGC的静态压缩试验结果.
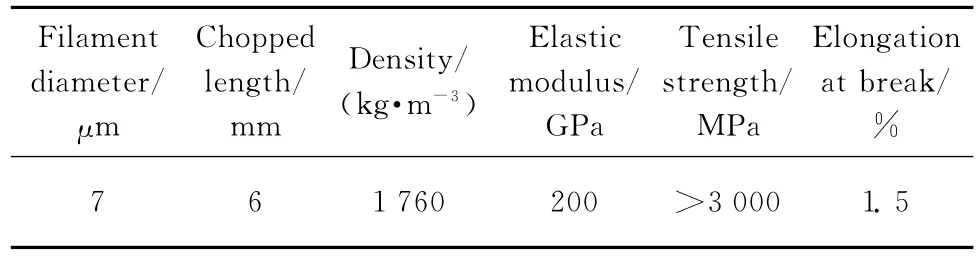
表1 碳纤维的物理、力学性能指标Table 1 Physical and mechanical properties of carbon fiber

表2 准静态抗压强度测试结果Table 2 Quasi-static compressive strength test results MPa
1.2 SHPB试验设备
SHPB[7]试验技术起初是用来研究金属、聚合物等材料的高应变率性能,发展至今已有60a,现已被广泛应用于混凝土等多种材料的动态力学性能测试.
冲击压缩试验在φ100的SHPB试验装置上进行.用于测试脆性材料的大直径SHPB试验存在以下缺点:端面摩擦效应、弥散效应明显;应力均匀性难以得到满足;恒应变率加载困难.从以下方面解决这些问题:在试件和压杆的端面均匀地涂抹上一层石墨与润滑剂的混合物,以确保端面摩擦效应的减少;采用波形整形技术[8].有大量试验表明,波形整形技术能有效降低弥散效应,同时还能通过一定技术参数的控制来实现应力均匀和恒应变率加载.
1.3 冲击压缩试验
1.3.1 SHPB试验有效性分析
图1给出了2CG试件的应变率时程曲线(˙ε-t曲线).由图1可见,通过一系列技术手段的控制能较好地实现试验过程中的近似恒应变率加载,保证了CFRGC的SHPB试验有效性.
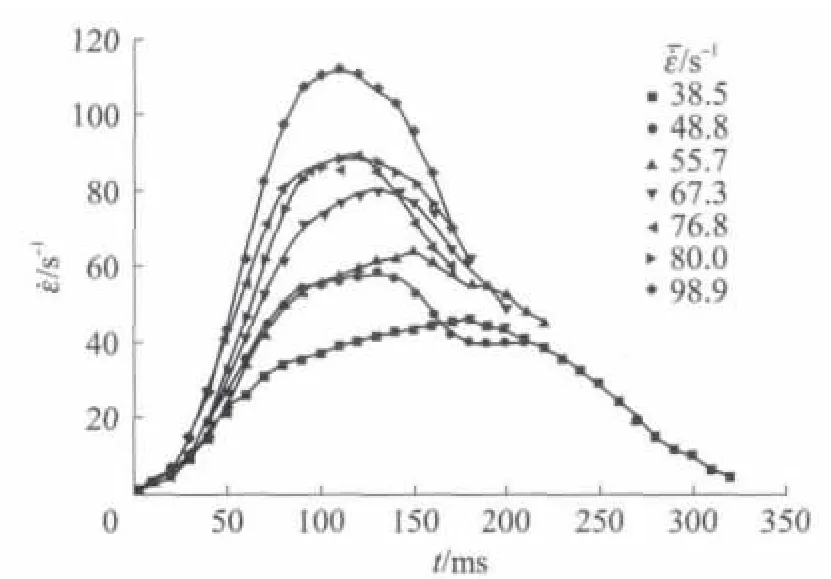
图1 SHPB试验过程中2CG试件的应变率时间历程曲线Fig.1 Strain rate-time history curve of 2CG specimen in SHPB testing
1.3.2 应力-应变曲线与破坏形态
SHPB试验的应力-应变(σ-ε)曲线如图2所示.由图2可见,在碳纤维体积分数相同的情况下,随着应变率的增加,CFRGC的动态压缩强度也随之增大.
图3给出了3CG试件的破坏形态.显然,随着应变率的增加,试件的破碎程度更为明显.在冲击荷载作用下,CFRGC要经过压实挤密、弹性变形、软化、屈服、微缺陷扩展、破坏等阶段,在这些阶段中试件始终和外界进行能量交换,将外部的机械能转变为应变能,又将应变能转化为塑性能、表面能等,并以声发射、动能等形式向外界释放能量.可以认为能量与试件的破坏息息相关,而这些能量主要体现在试件的损伤能上,因此破碎程度也可反映CFRGC能量特性的应变率效应.由此可见,CFRGC是一种应变率敏感材料.
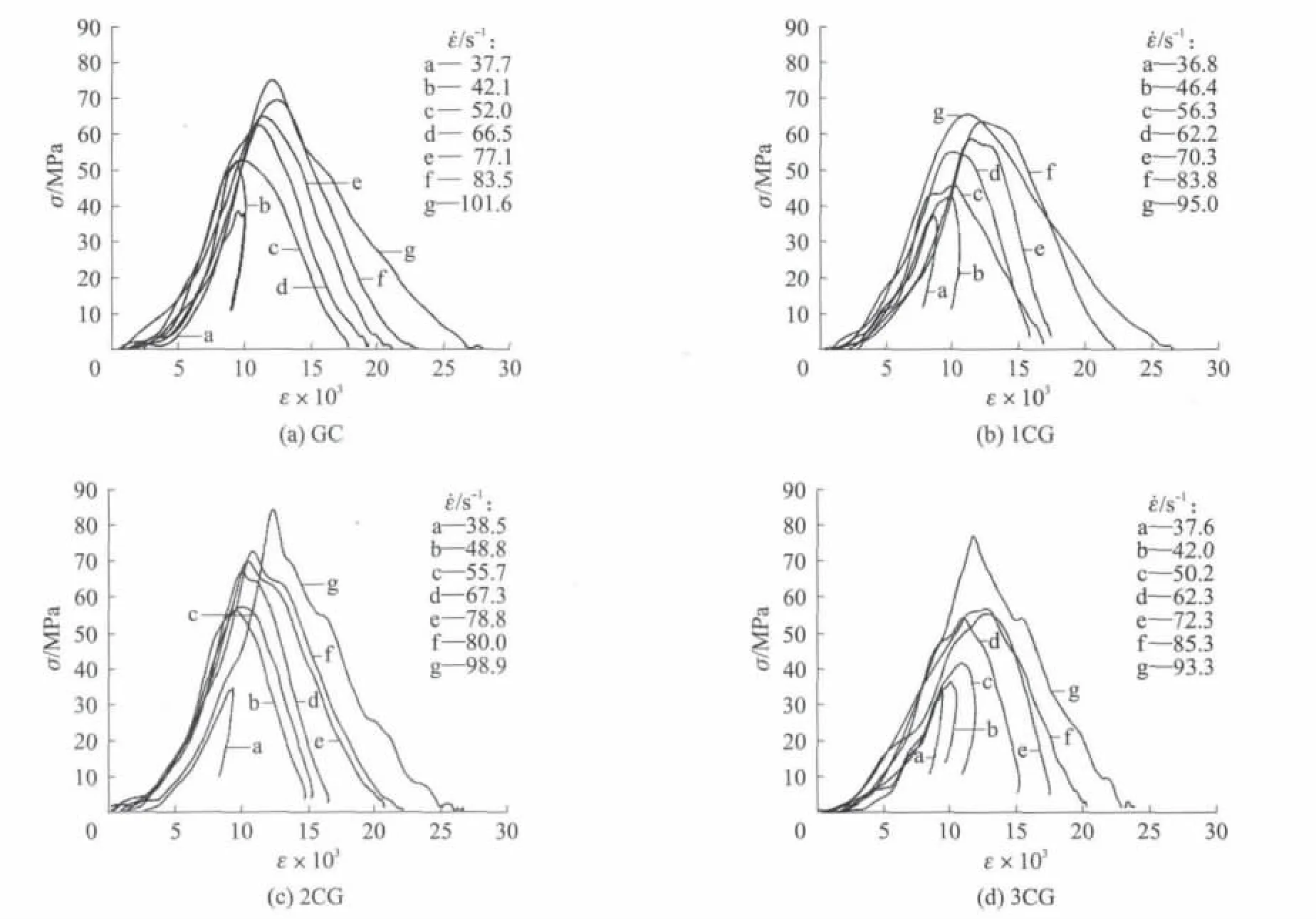
图2 碳纤维体积分数不同的CFRGC的SHPB试验应力-应变曲线Fig.2 Stress-strain curves of CFRGC with different fiber volume fraction

图3 SHPB试验后3CG试件的破坏形态Fig.3 Fracture morphology of 3CG specimen after SHPB testing
2 冲击韧性分析
2.1 韧性评价指标
韧性即为材料在一定荷载下所具有的变形能力,是材料延性和强度的综合.一般从宏观角度讲,韧性可定义为材料或结构从加载到失效为止吸收能量的能力.韧性不仅与材料强度有关,而且还取决于材料破坏时的变形量.
目前国内外评价纤维增强混凝土韧性的指标不尽相同.常用的一般有两种,一是峰值韧度Rp,其定义是:若假定应力-应变曲线中峰值点之前的部分为微裂纹稳定扩展阶段,之后的部分为微裂纹不稳定扩展阶段,则以应力-应变曲线的峰值点为分界,定义在峰值点之前应力-应变曲线的面积为峰值韧度Rp(见图4中的阴影面积),该指标反映了材料失稳前的完整力学响应,试验误差离散性较小,数据较韧度值可靠;二是比能量吸收[9](specific energy absorption,SEA),其物理意义是:单位体积的纤维增强地聚物混凝土吸收应力波能量的大小,该方法综合考虑了试验中多个影响因子,比较接近材料韧性的实际值,数学表达式为:
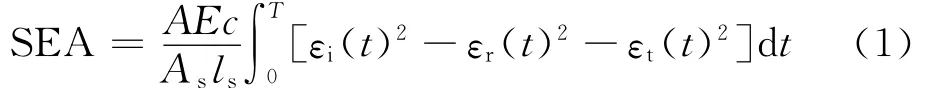
式中:E为杆的弹性模量;c为杆中波速;A,As分别为杆和试件的横截面积;ls为试件的初始厚度;εi,εr,εt分别为杆中的入射、反射、透射应变;T为试件完全破坏时刻.
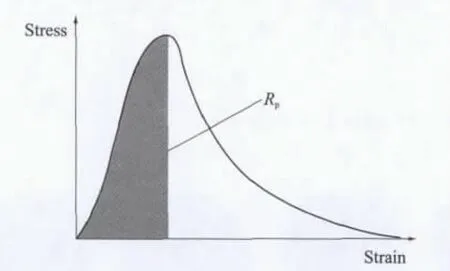
图4 Rp指标示意图Fig.4 Diagram of index Rp
2.2 峰值韧度评价
图5给出了Rp随应变率(˙ε)变化的规律.从图5整体趋势来看,Rp表现出了显著的应变率效应,即其随应变率的增加而增加.深入分析可知,在碳纤维体积分数相同的情况下,Rp和lg˙ε近似呈线性增长关系,如图6所示;对其线性拟合,得式(2):
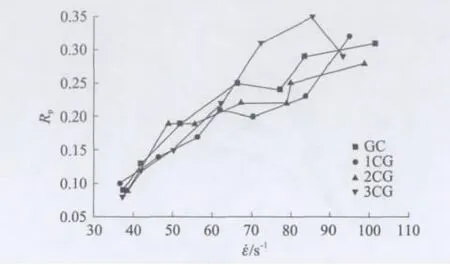
图5 峰值韧度Rp与应变率˙ε的关系Fig.5 Relationship between peak toughness and strain rate

图6 峰值韧度Rp与lg˙ε的关系Fig.6 Relationship between peak toughness and lgε˙
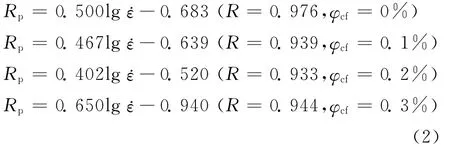
从峰值韧度的评价指标来看,通过对比拟合直线的斜率可知,CFRGC在碳纤维体积分数φcf为0.3%时能发挥出明显的冲击增韧优势.原因在于,碳纤维在混凝土内部构成了一种三维乱向分布的网络体系,这一乱向网络体系有助于提高混凝土受冲击时动能的吸收.在混凝土受冲击荷载作用时,纤维可以缓和混凝土内部裂缝尖端应力集中程度,并有效阻碍混凝土中裂缝的迅速发展,吸收由冲击荷载所产生的动能,从而提高混凝土的韧度.混凝土最终的破坏形态也能反映碳纤维的增韧效应.
2.3 比能量吸收评价
图7给出了SEA随应变率(˙ε)变化的规律.由图7的整体趋势来看,SEA表现出了显著的应变率效应,即其随应变率的增加而增加.深入分析可知,在碳纤维体积分数相同的情况下,SEA和lg˙ε近似呈线性增长关系,如图8所示;对其线性拟合,得式(3):
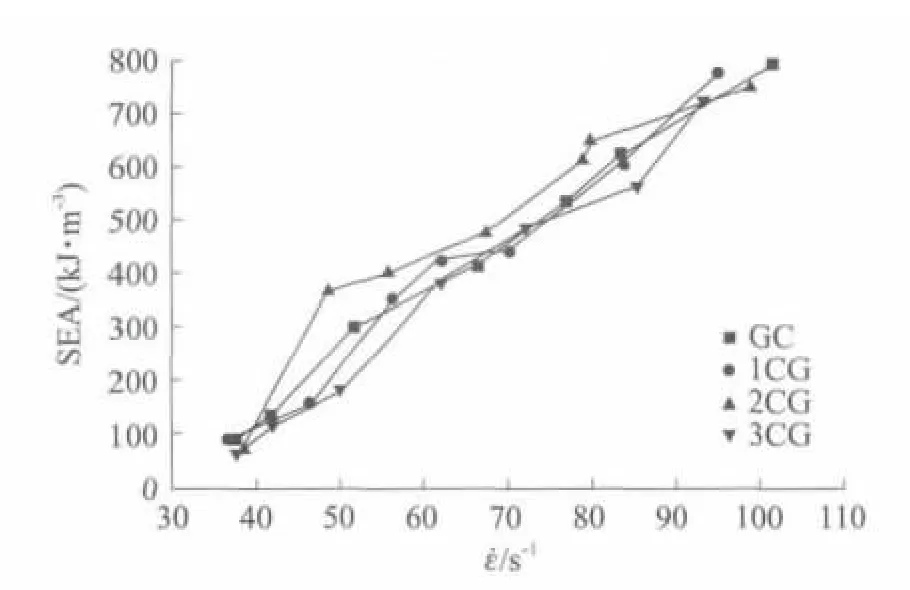
图7 SEA与应变率˙ε的关系Fig.7 Relationship between SEA and strain rate

图8 SEA与lg˙ε的关系Fig.8 Relationship between SEA and lg˙ε
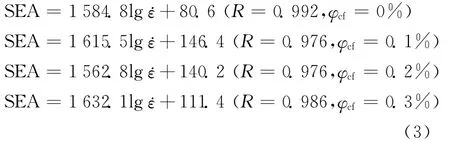
由此分析可知,从比能量吸收的评价指标来看,CFRGC在10~102s-1应变率范围内的韧性为64.0~786.9kJ/m3,表现出显著的应变率相关性,随应变率的增加而增加;碳纤维体积分数对SEA有一定的影响,对比拟合直线的斜率可知,碳纤维体积分数φcf为0.3%时的比能量吸收值随着应变率增加而增加的趋势相对较明显,但碳纤维体积分数为0.2%时的比能量吸收值则要比其他掺量下高,即CFRGC的冲击增韧优势在碳纤维体积分数为0.3%时表现得较为明显,但在碳纤维体积分数为0.2%时,碳纤维的增韧效果更为明显.
2.4 对比分析
整体看来,峰值韧度与比能量吸收随碳纤维体积分数变化的规律不尽相同,说明这2种表征冲击韧性的方法存在差异,但2种方法反映的发展趋势存在一致性,主要表现在以下方面:
(1)冲击韧性指标存在明显的应变率效应,即随着应变率的增加而增加.不少学者认为这是材料由一维应力状态向一维应变状态转换过程中的力学响应.由于进行SHPB的CFRGC试件都比较大,因此在SHPB试验中,试件内相当部位的受力状态已不能准确地定为一维应力,在冲击荷载作用下,由于材料的惯性效应,其侧向的应变受到限制,而且应变率越高,这个限制就越明显,从而有效地提高了其冲击韧性.
(2)对于CFRGC而言,碳纤维具有一定的增韧效果.CFRGC是存在大量微缺陷的复合材料,在加载初期损伤较小,基体材料的应变硬化起主导作用,其应力-应变曲线形态近似呈线性;随着荷载的增加,损伤演化加剧,大量微缺陷成核并扩展,断面处的碳纤维参与受力而形成损伤过渡区,增加了能量的耗散,推迟了裂纹的不稳定扩展,从而提高了CFRGC的韧性.理论上而言,碳纤维体积分数越大,CFRGC冲击韧性增加越明显.但由于实际浇注、搅拌等施工过程中存在较多不确定因素,导致纤维分散效果不佳,成团现象严重,因而在其体积分数较高情况下这种增加趋势并不特别明显.
(3)冲击荷载作用下,碳纤维在GC中的增韧效果更为明显.静态和动态下CFRGC的损伤演化方式有所不同,静态加载下,宏观裂纹的萌生来源于缺陷最多的过渡相区,扩展主要沿集料和砂浆的界面进行,最终的破坏是由主裂纹的失稳扩展导致的;冲击荷载下,加载的开始段在骨料相,砂浆相和过渡相同时萌生大量的微裂纹,参与受力的碳纤维数量越多,越有利于提高材料的韧性.
通过对比可以发现,采用比能量吸收作为冲击韧性评价指标的应变率效应更加明显,离散性较小,而且从指标的计算方法可以看出SEA综合考虑了试验中多个影响因子,比较接近材料韧性的实际值.因此,建议在评价碳纤维增强地聚物混凝土的冲击韧性时,采用SEA指标更加有效和合理.
3 结论
(1)从峰值韧度的评价指标来看,CFRGC在碳纤维体积分数为0.3%时能发挥出明显的冲击增韧优势.
(2)从比能量吸收的评价指标来看,在10~102s-1应变率范围内CFRGC的韧性表现出显著的应变率相关性,随应变率的增加而增加;CFRGC的冲击增韧优势在碳纤维体积分数为0.3%表现得较为明显,但在碳纤维体积分数为0.2%时,碳纤维的增韧效果更为明显,即CFRGC的增韧特性在碳纤维体积分数为0.2%和0.3%时相对较为优异.
(3)2种表征冲击韧性的方法所反映的发展趋势存在一致性,一是冲击韧性指标存在明显的应变率效应,即其随着应变率的增加而增加;二是碳纤维对于GC而言具有一定的增韧效果,而且在冲击荷载作用下,碳纤维在GC中的增韧效果更为明显.
(4)在评价碳纤维增强地聚物混凝土的冲击韧性时,采用比能量吸收指标更加有效和合理.
[1] IVORRA S,GARCÉS P,CATALÁG,et al.Effect of silica fume particle size on mechanical properties of short carbon fiber reinforced concrete[J].Materials &Design,2010,31(3):1553-1558.
[2] FU X,CHUNG D D L.Radio wave reflecting concrete for the lateral guidance in automatic highways[J].Cement and Concrete Research,1998,28(6):795-801.
[3] WEN Sihai,CHUNG D D L.Uniaxial tension in carbon fiberreinforce cement sensed by electrical resistivity measurement in longitudinal and transverse directions[J].Cement and Concrete Research,2000,30(8):1289-1294.
[4] 许金余,罗鑫,吴菲,等.地质聚合物混凝土动态劈裂拉伸破坏的吸能特性[J].空军工程大学学报:自然科学版,2013,14(5):85-88. XU Jinyu,LUO Xin,WU Fei,et al.Energy absorption capacities of geopolymer concrete under condition of splitting-tensile damage[J].Journal of Air Force Engineering University:Natural Science,2013,14(5):85-88.(in Chinese)
[5] SHI Caijun,DAY R L.A calorimetric study of early hydration of alkali-slag cements[J].Cement and Concrete Research,1995,25(6):1333-1346.
[6] 杨进勇,许金余,李为民,等.玄武岩纤维混凝土冲击压缩韧性[J].新型建筑材料,2008(6):69-72. YANG Jinyong,XU Jinyu,LI Weimin,et al.Impact compressure ductility of basalt fiber reinforeced concrete[J].New Building Materials,2008(6):69-72.(in Chinese)
[7] KOLSKY H.An investigation of the mechanical properties of materials at very high rates of loading[J].Proceeding Journal of American Physical Society,1949(B62):676-700.
[8] FREW D J,FORRESTAL M J,CHEN W.Pulse shaping techniques for testing brittle materials with a split Hopkinson pressure bar[J].Experimental Mechanics,2002,42(1):93-106.
[9] LU G,YU T Y.Energy absorption of structures and materials[M].London:Woodhead Publishing,2003:20-96.

