选择期权的定价

郑州升达经贸管理学院 傅 钰

一、期权简介

期权作为一种金融工具是在远期业务基础上产生的。它可以被看作是一种附加了特殊条件的远期业务。在这种有价的标准化金融合约中规定了合约的买方有权力（并非义务）在未来一个确定的时间点按照事先约定的价格（即Basisprice）买入（看涨期权）或卖出（看跌期权）一种有价证券或是一种物品（即合约的标的物）。

期权按照一般的划分方法有两种不同的类型：欧式期权和美式期权。在欧式期权中，合约的买方只能在合约规定的时间点行使其权利。而在美式期权中买方可以在约定的时间段内的任何时刻行使这种权利。这两种不同的类型是期权的基本形式，人们标之为

标准期权。随着经济的不断发展，从标准期权中衍生出无数的其他类型的期权，比如：栅栏期权（Barrier-Optionen），百慕达期权（Bermuda Optionen），亚洲期权（Asiatische Optionen），回看期权（Lookback Optionen），选择期权（Chooser Optionen）等。这些非标准的期权被人们统称为外来期权（或奇异期权）。这些期权实际上是包含了标准期权的特点，同时附加了特别客户的特定要求的特殊的金融合约。

选择期权（Choose Option）是外来期权的一种。大约在1990年7月出现在伦敦，它是一种特殊的场外交易品种。选择期权也被称为“pay-now-choose-later-Option”。它是由一个欧式看涨期权和一个欧式看跌期权共同组成的（即所谓的“券中券”）。在这种期权中，合约的买方在签订合约后，同时拥有欧式买入和卖出两种期权。然后，在合约规定的时间点，他有权根据标的物价格的近期波动做出决定，选择一种期权类型（看涨期权或是看跌期权）以备日后执行。在合约最后的执行日期，买方有权决定他之前选择的期权最终要不要行权。通过购买这种合同，投资者等于对剧烈的价格波动做了两个方向的保险，比单纯购买一份看涨或看跌期权更灵活，更安全，并且又比“long Straddle”（即同时购买看涨看碟两份期权，也即多头跨式期权）降低了成本。选择期权有两种类型：“简单型”和“复杂型”。在“简单型”选择期权包含的的看涨期权和看跌期权的标的物的执行价格（即Basisprice）、执行日期是相同的。在“复杂型”中包含的两个期权（看涨期权和看跌期权）有着不同的执行价格或执行时间，或这两者都不相同。

为了使分析更容易理解，本文首先推演常见的“简单型”选择期权（其标的物为有价证券，比如一支股票）。然后，用同样的方法，进一步研究“复杂型”的选择期权。本文中提到的选择期权合约中的时点反映在下面的时间轴上（见图1）：

图1

在这个时间轴上，t0是期权合约签订的时点。在时点t1，期权合约的买方根据标的物的价格走势对选择哪种期权做出决定。在T时点期权合约到期，买方决定最终要不要执行手中持有的期权合约。

二、“简单型”选择期权的定价

提到期权的定价，一定会涉及到Black-Scholes模型。这是一个被广泛接受和认可的典型的期权定价模型。它是由费雪布莱克（Fisher Black）和米荣绶勒斯（Myron Scholes）在1973年共同发表的。这个模型给出的定价理论无论是对金融市场或是金融市场的参与者都产生了很大的影响。该模型建立在一些限定的假设上，比如假设作为期权合约标的物的价格是呈对数正态分布的，金融市场中的利率是非随机变化的。同时模型中不考虑税收、交易和其他的费用。模型假设市场在任何时点都是开放的，任何时候任何金额和单位的交易都可以执行，并且对当时的交易价格不产生影响。

在建立一个金融市场模型之前，首先需要定义一些概念和符号Sandmann.（2001）：

（Ω，F，P*）是本文研究的样本空间，其中Ω表示所有随机事件的集合。{Ft}t∈[t0，T]是由 n维布朗运动（Brownian Motion）产生的Filtration，Ft包含了截止到t时点的所有关于价格波动过程的信息。P*表示等价于原始客观概率Martingal单位的同价衍生的Martingal单位，在概率P*下的所有价格波动过程中都不能进行无风险的套利活动。

{W*（t）}t∈[t0，T]表示了在同价衍生 Martingal单位下的 n维布朗运动的路径。W*（t）的每一时段的增量 W*（t1）-W*（t0），W*（t2）-W*（t1），…，W*（tn）-W*（tn-1）之间呈随机不相关的分布。并且对于任意一个时间段 u-t＞0来说，W*（t）的增量 W*（u）-W*（t）呈正态分布。

即：W*（u）-W*（t）～N（0，（u-t））

{S（t）}t∈[t0，T]是作为标的物的有价证券（股票）的随机价格波动过程。它与同时点的Filtration{Ft}t∈[t0，T]相对映，并且是下面随机微分方程的解：

dS（t）=μ·S（t）·dt+σS·S（t）dW*（t）

其中，μ表示价格随机变化的趋势（即价格的期望值）；σS表示这个有价证券价格的不稳定程度（即价格的波动率）。

在同价衍生Martingal单位P*下，这支股票的瞬时价格为：

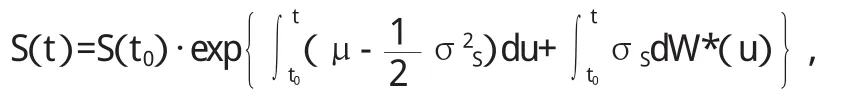
其中，μ=r；r是以对数形式表示的无风险利率（conform interest），即是无风险的年利率。

在Black-Scholes模型中，看涨和看跌期权的无套利价格（Arbitrageprice）分别是：

Call[S（t），K，t，T]=S（t）·e-di(T-t)·N（d1）-K·e-r(T-t)·N（d2）

Put[S（t），K，t，T]=K·e-r(T-t)·N（-d2）-S（t）·e-di(T-t)·N（-d1）

在利率非随机变化的假设下，一个标的物为一支股票S（t），到期日为T，执行价格（即Basisprice）为K的简单型选择期权在t1时的无套利价格（即Arbitrageprice）为：

其中：Call[S（t1），K，t1，T]是 t1点时看涨期权的无套利价格；Put[S（t1），K，t1，T]是 t1点时看跌期权的无套利价格

为了在T时点得到较大的预期收益，期权合约的购买者会在t1点比较看涨和看跌期权在这一时点对T点的预期收益，即他们会比较t1点时看涨和看跌期权的无套利价格，然后选择那个有较大值的期权继续持有。因此可以对上述简单型选择期在t1时的无套利价格进行改写：

在“简单型”选择期权合约中，看涨和看跌期权有同样的标的物，同样的执行价格，同样的执行日期。所以可以用HansR.Stoll的“Put-Call Parity”（即看涨看跌期权等价关系）来表示它们之间的这种关系。1969年，Hans R.Stoll定义了看涨和看跌期权无套利价格之间的等价关系：

Put[S（t1），K，t1，T]=Call[S（t），K，t，T]-S（t）·e-di(T-t)+K·e-r(T-t)

现在，这中等价关系是在时点t1，因此有：

Put[S（t1），K，t1，T]=Call[S（t1），K，t1，T]-S（t1）·e-di(T-t1)+K·e-r(T-t1)

所以上述选择期权在t1时的无套利价格就可以改写成：

A（t1）=Call[S（t1），K，t1，T]+max{K·e-r(T-t1)-S（t1）·e-di(T-t1)，0；t1}

其中：max{K·e-r(T-t1)-S（t1）·e-di(T-t1)，0；t1}可以看作是一个标的物为 S（t1）·e-di(T-t1)，执行价格为 K·e-r(T-t1)，执行日期为 t1的新的看跌期权在 t1时点的无套利价格，即 max{K·e-r(T-t1)-S（t1）·e-di(T-t1)，0；t1}=Putneu[S（t1）·e-di(T-t1)，K·e-r(T-t1)，t1，t1]

则上述选择期权在t1时的无套利价格可以进一步写成：

A（t1）=Cal[S（t1），K，t1，T]+Putneu[S（t1）·e-di(T-t1)，K·e-r(T-t1)，t1，t1]

那么在t0时这个简单选择期权的无套利价格为：

A（t0）=Cal[S（t0），K，t0，T]+Putneu[S（t0）·e-di(T-t1)，K·e-r(T-t1)，t0，t1]

所以一个简单型的选择期权在t0时的无套利价格（Arbitrageprice）可以看作其包含的看涨期权和一个新的看跌期权的无套利价格和。这个新的看跌期权具有一个和原来看跌期权不同的股票（在t0时股票价格为S（t0）·e-di(T-t1)），不同的执行价格（在t0时执行价格为K·e-r(T-t1)）和不同的执行期间（t0点签订合约，t1点执行）。

在Black-Scholes模型中，t0时这个简单选择期权的无套利价格为：

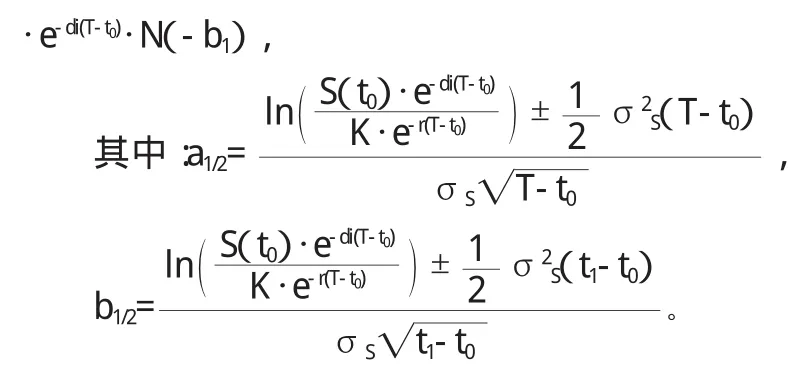
三、“复杂型”选择期权的定价

在“复杂型”选择期权中，看涨和看跌期权有着不同的执行价格（即Basisprice）或者不同的执行时间，或者两者都不一致。本文研究两者都不一致的情况。

利率非随机变化的条件下，一个复杂型选择期权的在t0时的无套利价格为：

ACOM（t0）=max{Call[S（t0），KC，t0，TC]，Put[S（t0），KP，t0，TP]；t1}

这里KC和KP分别表示看涨期权（C）和看跌期权（P）的执行价格，TC和TP分别表示它们的执行时间。

Rubinstein在他的题为“Option for the Undecided”（1991）的论文中曾经证明，利率非随机变化的条件下复杂型选择期权的无套利价格可以通过二元正态分布计算出来：

m1/2中的参数“I”是下面方程的解：

N（a，b，ρ）表示一个二元正态分布的概率，它表示两个随机变量共同的分布情况。其中每一个随机变量自身都是呈正态分布的。

对于包含两个随机变量X和Y的二元正态分布（X，Y）～N（μ，∑）：

它们共同的密度函数为：

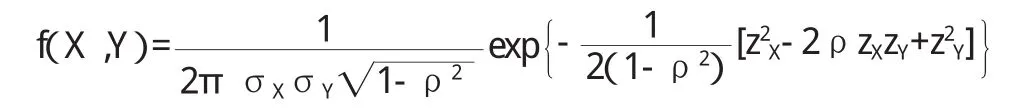
本文只研究标准二元正态分布的情况，即两个随机函数的期待值和方差分别为：E[zX]=0，Var[zX]=1，E[zY]=0，Var[zY]=1。

四、结论

重要参数“I”的值可以通过“Newton-Raphson”的方法计算出来。利用Mathematica5.0软件这个值可以很容易算出。并且对于任

本文研究了期权场外交易的重要品种——选择期权的定价问题，分别就“简单型”和“复杂型”选择期权的定价展开讨论。文章推演了“简单型”选择期权的定价，即通过Black-Scholes模型和Hans R.Stoll的“Put-Call Parity”来解决。针对“复杂型”选择期权的定价，本文选择了Rubinstein和“Newton-Raphson”的方法来计算。该模型对于我国银行和投资者个人都具有一定的适用价值。

［1］ Black,F.und Scholes,M.(1973):The Pricing of Options and Corporate Liabilities,Journal of Political Economy 81,S.637-654.