光子晶体滤波器的滤波品质调制因素研究

苏安，李忠海，莫传文，蒙息君，蒋丹，杨德贵

(河池学院 物理与机电工程学院，广西 宜州 546300)

0 引言

光子晶体［1－2］及其特殊的光学特性，已经成为近半个世纪以来物理学界研究的主要热点之一［3－14］。其中光子晶体的禁带特性及禁带中的缺陷模(窄透射峰)结构，是制备新型光学滤波器件的主要依据［4－9］。当前，研究光子晶体或光子晶体量子阱构成的滤波器件报道文献已经不少［4－9］，但系统总结归纳并对比各种结构因素对光子晶体滤波器滤波品质的调制(或影响)，还未见文献报道。滤波品质是衡量光学滤波器件的主要性能及应用价值的重要指标之一。对于光子晶体或光子晶体量子阱滤波器，一般以透射峰中心对应的波长(或频率)除以透射峰的半高全宽来计量其品质(Q=λc/Δλ)，也称品质因子，品质因子越大，滤波性能越好［4－7］。

基于这个思路，本文分别构造不同的光子晶体或光子晶体量子阱(简称光量子阱)模型，并利用传输矩阵法理论，通过数值计算、绘图的方式，直观地绘制光子晶体或光子晶体量子阱滤波器的滤波效果。然后分别研究排列周期数、基元介质折射率、介质正负折射率和介质层厚度等因素对滤波器品质的调制规律，力图从理论上为光子晶体滤波器的制备或调制方法提供参考。

1 研究方法

研究方法采用传输矩阵法。传输矩阵法是时下研究一维光子晶体能带结构最直观、最成熟和最常用的方法之一。方法的核心是用一传输矩阵即可描述光在某层薄膜介质中的传播行为，光在多层薄膜介质周期性排列形成的光子晶体中传播行为可用各层介质对应的传输矩阵相积来描述，通过相积得到的总传输矩阵就可以计算出光在光子晶体中传输的电场分布、透射系数、反射系数、透射率和反射率等。鉴于传输矩阵法理论已经比较成熟且详细报道的文献比较多，在此不再赘述，详细可见文献［9］和［14］。

2 计算结果与分析

2.1 排列周期数对光子晶体滤波器滤波品质的调制

构造镜像对称结构光子晶体模型(AB)n(BA)n，其中A、B为周期性排列的光子晶体两种基元介质，它们分别是:A介质为碲化铅(PbTe)，折射率na=4.1，介质层厚度da=762.8 nm，B介质为硫化锌(ZnS)，折射率nb=2.35，介质层厚度db=1 330.85 nm。n是光子晶体的排列周期数，一般取正整数。

取光子晶体的排列周期为n=2、3、4、5，其他参数不变，分别计算模拟出光子晶体的透射能带谱，如图1所示。

图1显示，随着排列周期数n的正整数增大，光子晶体禁带中的中心透射峰变得越来越精细，同时光子晶体的禁带会越来越规整，如图1(a)～(d)所示。n=2、3、4、5时，中心透射峰对应的半高全宽 Δλ分别为:Δλ2=0.028 4ω/ω0、Δλ3=0.008 5ω/ω0、Δλ4=0.002 7ω/ω0和Δλ5=0.000 9ω/ω0。由于光子晶体是镜像对称结构，光子晶体禁带中心恒定出现单条透射峰，即禁带中的单透射峰中心λc均位于1.0ω/ω0频率位置。则根据滤波品质的计算公式Q=λc/Δλ可得出对应透射峰的透射品质，即滤波品质分别为:Q2=0.035 2×103、Q3=0.117 5×103、Q4=0.365 0 ×103和Q5=1.102 5 ×103。

可见，随着光子晶体排列周期数的整数倍增大，光子晶体禁带中的透射峰会越来越精细，即由该光子晶体构造成的光学滤波器的滤波品质会越来越高、滤波性能会越来越好。根据这个规律可以以周期数来调制光子晶体滤波的品质［6，11］。

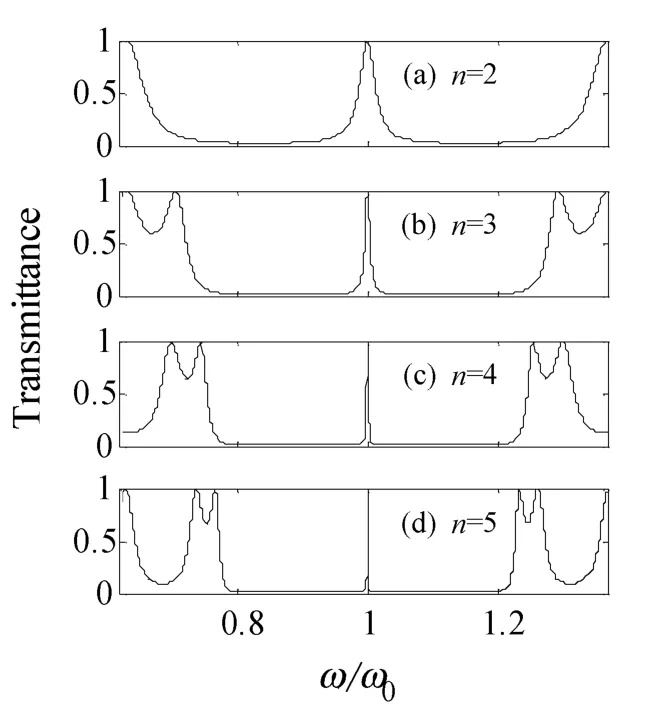
图1 光子晶体(AB)n(BA)n的透射谱

2.2 基元介质折射率对光子晶体滤波器滤波品质的调制

仍然以2.1中的镜像对称结构光子晶体模型(AB)n(BA)n为研究对象，固定光子晶体的排列周期数为5，而取A层介质的折射率na=3.2、3.5、3.8和4.1逐渐递增，其他参数不变，可分别计算模拟出光子晶体(AB)5(BA)5随A层介质折射率变化的透射能带谱，如图2所示。

从图2可见，当A层介质的折射率增大时，光子晶体禁带中的中心透射峰也会变得越来越精细，而且该透射峰还向高频方向移动，同时禁带会越来越宽，如图 2(a)～(d)所示。na=3.2、3.5、3.8、4.1时，中心透射峰中心的频率 λc位置分别为:λc3.2=0.980 9ω/ω0、λc3.5=0.984 5ω/ω0、λc3.8=0.991 0ω/ω0和 λc4.1=1.000 0ω/ω0，中心透射峰对应的半高全宽 Δλ 分别为:Δλ3.2=0.007 3ω/ω0、Δλ3.5=0.003 5ω/ω0、Δλ3.8=0.0017ω/ω0和 Δλ4.1=0.000 9ω/ω0。根据滤波品质的计算公式Q=λc/Δλ可得出对应透射峰的透射品质，即滤波品质分别为:Q3.2=0.136 6 ×103、Q3.5=0.287 4 ×103、Q3.8=0.583 1 ×103和Q4.1=1.111 1 ×103。

即随着光子晶体基元介质高折射率介质折射率的增大，光子晶体禁带中的透射峰会越来越精细，即光子晶体滤波器的滤波品质也会越来越高、滤波性能会越来越好［3，10］。

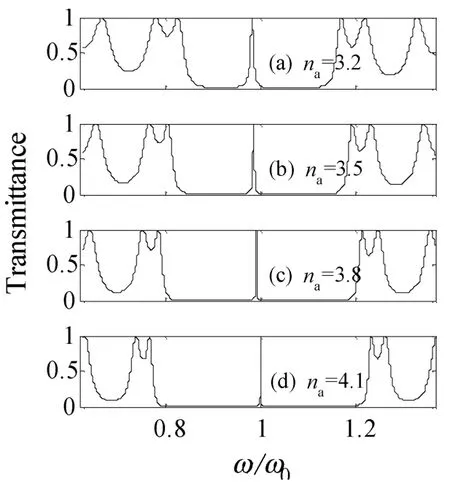
图2 光子晶体(AB)5(BA)5的透射谱

同样地，类似于普通结构光子晶体，当光子晶体量子阱的垒层高折射率介质的折射率越大，光子晶体量子阱滤波器的滤波品质也会越高［10－11］。光子晶体量子阱的定义:当中间层光子晶体块的能带完全处于两侧光子晶体块的禁带中时，构成光子晶体量子阱结构，中间层光子晶体块称为光量子阱的阱，两侧光子晶体块称为光量子阱的垒［3－6］。取一维光子晶体量子阱结构模型(AB)m(BAB)n(BA)m和(TB)m(BAB)n(BT)m为研究对象，各介质层分别是:A为硫化砷(AsS)，εA=6.760，dA=736.0 nm，B为二氧化硅(SiO2)，εB=2.102 5，dB=131 8.0 nm，T 为碲化铅(PbTe)，εT=16.810，dT=467.0 nm，m、n是光子晶体介质层排列周期数。此时，光子晶体(BAB)n为两光量子阱结构的阱层，(AB)m(AB)m和(TB)m(BT)m分别为两光量子阱结构的垒层。

当n=2，m=5，其他参数不变时，通过计算机编程数值计算模拟，可绘制出光子晶体量子阱结构(AB)5(BAB)2(BA)5和(TB)5(BAB)2(BT)5的透射能带谱，如图3所示。

图3显示，光量子阱(AB)5(BAB)2(BA)5和(TB)5(BAB)2(BT)5均在禁带中出现3条分立且透射率为100%的共振透射峰，但光量子阱(TB)5(BAB)2(BT)5的分立透射峰比(AB)5(BAB)2(BA)5的精细，而且后者禁带也宽于前者。以禁带中心849.8 nm波长位置的窄透射峰为例，光量子阱(AB)5(BAB)2(BA)5透射峰的半高全宽为ΔλAB=0.058 6 nm，对应的滤波品质QAB=1.450 2×104，而光量子阱(TB)5(BAB)2(BT)5相应透射峰的半高全宽为ΔλTB=0.000 7 nm，对应的滤波品质QTB=1.214×106。可见，后者的滤波品质远高于前者。从两者的结构来看，它们的阱层结构完全相同，但垒层的高折射率介质不同，光量子阱(TB)5(BAB)2(BT)5垒层高折射率介质T的折射率(nT=4.1)明显大于(AB)5(BAB)2(BA)5垒层高折射率介质A的折射率(nA=2.6)。

所以，对于光量子阱结构，可通过调节垒层高折射率介质的折射率来调制光子晶体滤波器的滤波品质，从而改变滤波器的性能。由于自然介质的折射率是有上限的，因此上述调制方法在一定折射率范围内有效。近两年作者提出并报道了“通过改变光量子阱垒、阱层周期数来改变垒、阱层的折射率和的比值，即可快速提升光量子阱滤波器的滤波品质，或者通过在介质中掺入激活杂质也可以快速提升光量子阱滤波器的滤波品质”，这些方法可以有效避开自然介质折射率上限问题［4－6］。

图3 一维光量子阱的透射谱(a)(AB)5(BAB)2(BA)5(b)(TB)5(BAB)2(BT)5

2.3 介质折射率正负对光子晶体滤波器滤波品质的调制

构造光子晶体模型(AB)6(CBAABC)(BA)6，A与B介质层为双正介质，分别为玻璃和硒化锌，C为掺杂材料，nA=1.5，nB=2.5，nC=1.6(当为双负介质时nC= －1.6)，nAdA=nBdB= λ0/4，nCdC=2λ0(当为双负介质时为 －2λ0)，(λ0是禁带中心频率 ω0对应的波长)。分别在C层为双正介质(nC=1.6)和双负介质(nC=－1.6)的情况下计算绘制光子晶体的透射谱，如图4所示。

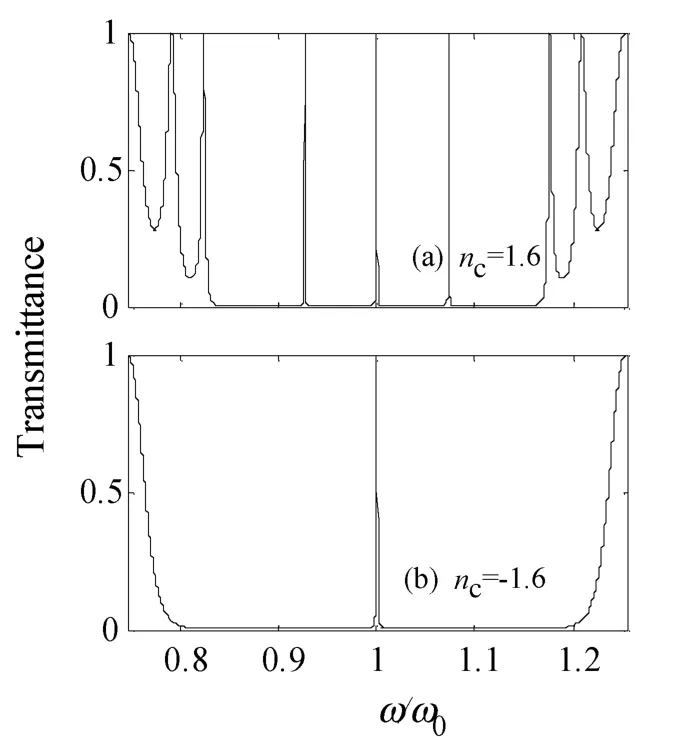
图4 光量子阱(AB)6(CBAABC)(BA)6的透射能带谱

从图4可见，当C层介质从双正介质替换成双负介质时，光子晶体主禁带中的分立透射峰出现简并现象，由双正时的3条简并为双负时的1条，而且简并后的透射峰较简并前的粗，同时简并后的禁带比简并前的宽。以禁带中心透射峰为例，nC=1.6时，其半高全宽为Δλ正=0.425 0×10－3ω/ω0，滤波品质为Q正=2.352 9×103;当nC= －1.6时，其半高全宽为 Δλ负=0.829 0×10－3ω/ω0，滤波品质为Q负=1.206 3×103。

可见，在其他参数不变的情况下，当C层介质由双正介质变成双负介质时，光子晶体滤波器的滤波品质不仅不升高，且是下降的，从这个特性来看，在制备宽禁带范围带宽相对较宽的光学滤波器时，可选择双负介质薄膜。当然，根据报道的文献可知，当双负介质的折射率负值增加时，光子晶体滤波器的滤波品质将会升高，这也为提高光子晶体滤波器件的滤波品质提供理论依据［12－13］。

2.4 介质厚度对光子晶体滤波器滤波品质的调制

以光子晶体模型(ABD)6(CBA)5(ABD)6(CBA)5为研究对象，其中A、C介质为电单负材料，B、D介质为磁单负材料，各介质的磁导率和介电常量为:

式中的 ω 表示频率(单位为GHz)，α 和β 为电路参数，εa、μa和 εb、μb均为常量，取值为 εa=μb=2，μa=εb=3，α =β=100，dA=6 mm，dB=15 mm，dC=18 mm，dD=6 mm、12 mm。

其他参数不变的情况下，由单负材料的传输矩阵，即可计算和绘制出光子晶体(ABD)6(CBA)5(ABD)6(CBA)5的透射能带谱，如图5所示。

由图5可见，当 D层介质的厚度增大时，光子晶体(ABD)6(CBA)5(ABD)6(CBA)5的透射峰变窄，即由光子晶体构成的光学滤波器的滤波品质升高。以图5右侧的透射峰为计算对象，当dD=6 mm时，其半高全宽为Δf6mm=0.157 0×10－3GHz，滤波品质为Q6mm=0.046 5×105;当dD=12 mm时，其半高全宽为Δf12mm=0.007 1×10－3GHz，滤波品质为Q12mm=1.029 7×105。即由光子晶体某介质层的厚度亦可调制由其制成的滤波器的滤波品质［7，9］。

因此光子晶体或光子晶体量子阱滤波器的滤波品质可由光子晶体排列周期数、介质折射率及介质折射率的正负值，以及介质的物理厚度等来调制，且调制的正负机制不一样。另外，根据相关文献报道，光子晶体或光子晶体量子阱滤波器的滤波品质还可以通过光学厚度等参量来调制，鉴于文章的篇幅或调制机制的相似性，在此不一一列举。

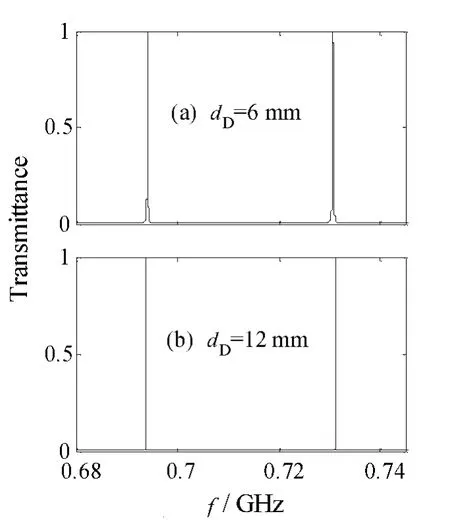
图5 光子晶体(ABD)6(CBA)5(ABD)6(CBA)5的透射能带谱

3 结论

通过传输矩阵法理论，研究光子晶体或光子晶体量子阱滤波器滤波品质的调制机制，得出如下结论:

(1)通过调整光子晶体的排列周期数、基元介质高折射率介质的折射率、光子晶体介质层厚度等，均可提高光子晶体或光子晶体滤波器的滤波品质。

(2)当光子晶体中的某介质层由双正介质替换成双负介质时，光子晶体滤波器的滤波品质会下降，但随着双负介质层的折射率负值增加，滤波器的滤波品质会上升。

结构参数对光子晶体或光子晶体量子阱滤波器滤波品质的这种作用机制，为制作新型光学滤波器件及其建立调整机制提供有效地理论依据。

［1］E Yablonovitch.Inhibitedspontaneousemissioninsolid－ statephysicsandelectronics［J］.Phys.Rev.Lett.，1987，58(20):2 059 －2 061.

［2］S John.Stronglocalizationofphotonsincertaindisordereddielectricsuperlattices［J］.Phys.Rev.Lett.，1987，58(23):2 486 －2 489.

［3］苏安，高英俊.双重势垒一维光子晶体量子阱的光传输特性研究［J］.物理学报，2012，61(23):234208.

［4］苏安，蒙成举，高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制［J］.中国激光，2014，41(3):0306001.

［5］苏安，蒙成举，高英俊.实现高品质滤波功能的一维光子晶体量子阱滤波器［J］.中国激光，2013，40(10):1006001.

［6］苏安，蒙成举，高英俊.结构周期数对光量子阱透射品质的影响研究［J］.激光与光电子学进展，2013，50(1):012302.

［7］邓新华，刘念华，安丽萍.基于单负材料光子晶体异质结构的可调多通道滤波器［J］.科学通报，2009，54(10):1 405－1 409.

［8］苏安.实现多通道光滤波与放大功能的光子晶体量子阱［J］.红外与激光工程，2013，42(3):727－732.

［9］苏安.单负材料一维光子晶体超窄带滤波特性研究［J］.光学技术，2013，39(2):145－150.

［10］苏安，何奇文，梁玉娟.垒层介质折射率对光量子阱透射谱的影响［J］.河池学院学报，2013，33(5):25－28.

［11］苏安，许江勇.周期数对光量子阱透射谱的影响［J］.河池学院学报，2013，33(2):45－48.

［12］许江勇，苏安，潘继环，等.双负介质对一维光子晶体量子阱透射谱的影响［J］.红外与激光工程，2013，42(8):2 156－2 161.

［13］苏安，彭金松，潘继环，等.左手介质对一维光量子阱透射谱的影响［J］.广西物理，2013，34(3):27－30.

［14］王辉，李永平.用特征矩阵法计算光子晶体的带隙结构［J］.物理学报，2001，50(11):2 172－2 178.