模糊时间序列模型在滑坡预测预报中的应用

陈 伟，张 践

（1.武汉科技大学 城市建设学院，湖北 武汉 430000；2.武汉大学 测绘学院，湖北 武汉 430079；3.武汉际上空间科技有限公司，湖北 武汉430070）

模糊时间序列预测结合了经典的时间序列分析理论和新兴的模糊数学理论，能有效地克服数据的不完整性和不确定性。模糊时间序列的研究受到了众多国内外学者的关注。1993 年Song 和Chissom[1]提出了模糊时间序列模型并用于对 Alabama大学招生人数的预测；又提出了一个新的模糊时间序列模型并与其他模型进行比较，使得预测精度得到很大提高[2,3]。此后，越来越多的专家和学者从理论和应用等多方面对模糊时间序列模型进行了更加深入的研究[4-8]。本文在前人研究的基础上，将模糊时间序列预测模型应用到滑坡预测预报中，具有一定的实用价值。

1 模糊时间序列预测模型

1.1 相关定义

定义1 令U为给定论域，将论域划分为 n 个子区间，则U={u1,u2,…,un}。一个定义在论域U中的模糊集合A表示如下：A=fA(u1)/u1+fA(u2)/u2+…+fA(un)/un。其中，fA(•)是 ui对模糊集合 A 的隶属函数 ；fA(ui)是 ui对模糊集合A的隶属度，fA(ui)Î[0,1]，i=1,2,…,n。

定义2 令R中一子集Y(t) ( t = …, 0, 1, 2, … )为给定论域，fi(t) (i = 1, 2, …)为定义在其上的模糊集合，由f1(t)，f2(t)，…组成的集合F(t)称作定义在 Y(t) ( t = …,0, 1, 2, …)上的模糊时间序列。

定义3 如果存在一个模糊关系R(t,t-1)，并有F(t)=F(t-1)◦R(t-1,t)，则称 F(t)可由 F(t-1)通过模糊关系R(t,t-1)导出。其中，“◦”为一种关系运算算子。若F(t-1)=Ai，F(t)=Aj，则 F(t-1) 与 F(t)之间的模糊逻辑关系可以表示为F(t-1)→F(t)。

定义4 具有相同前件的模糊逻辑关系可以进一步构成模糊逻辑关系组。假设一组模糊逻辑关系：Ai→Aj1，Ai→Aj2，…，则对应的模糊逻辑关系组为Ai→ Aj1，Aj2，…。

1.2 模糊时间序列模型预测步骤

本文建立模糊时间序列模型的具体步骤如下：

1）定义论域及区间划分。定义论域U=[Dmin-δ1,Dmax+δ2]，其中Dmin、Dmax分别为历史数据的最小值和最大值；δ1、δ2为2个合适的正数。根据模糊聚类算法得到样本中心点，将2个相邻的聚类中心的中点作为论域划分的边界点，将论域U划分为不等长度的区间u1，u2,…， un，其对应的中心分别为 m1，m2，…， mn（具体步骤见文献[9]）。

2）定义模糊集并模糊化数据。根据上步得到的区间定义模糊集 A= (A1， A2， …， An)，其中，Ai表示模糊集A的语义变量。将历史数据按式（1）模糊化，其中，fij表示uj对集合Ai的隶属度，本文采用的隶属函数为三角隶属函数。为了简化计算，本文采用的模糊化规则是：首先判断数据x所在区间，若x所在的区间为ui，那么就把x模糊化为Ai。依次将所有数据模糊化，就得到了一个模糊时间序列。

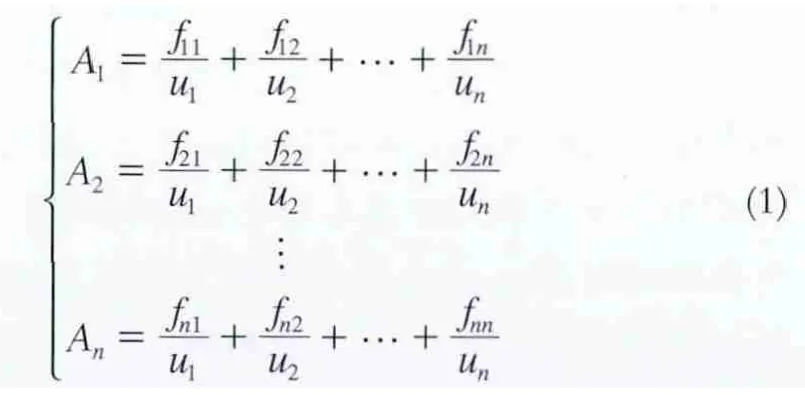
3）建立模糊关系并预测。根据步骤2）所得到的模糊时间序列求模糊关系矩阵。选用n天的样本数据作为训练数据，设当天为t，则前一天为t-1。选取训练样本，根据选取的训练样本，找出模糊关系矩阵。假设某日训练样本的模糊化结果为Ft,m，下一日的数据模糊化结果为Ft+1,n，则模糊关系为Ft,m→Ft+1,n，根据模糊关系求模糊关系矩阵R。

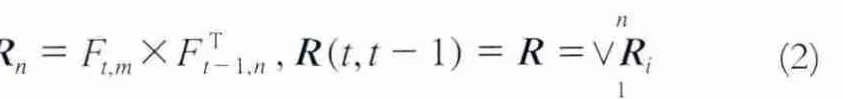
式中，×为取小运算；Ú为取大运算。将F(t-1)采用三角模糊函数模糊化，建立模糊时间序列预测模型：F(t)=F(t-1)◦R(t-1,t)。

4）将输出结果去模糊化，得到预测数值。本文采用最大隶属度法去模糊化，运算规则如下：如果F（t）模糊预测变化值隶属函数有且只有一个最大值un，其中点为mn，则预测变化值为mn；如果F（t）模糊预测变化值隶属函数有多个最大值u1，u2,…，un，它们的中点分别为m1，m2,…，mn，则预测变化值为（m1+ m2+…+mn）/n；如果F（t）模糊预测变化值隶属函数全部为0，则预测变化值为0。

2 应用实例

本例取自文献[10]中的应用实例，著名的洒勒山滑坡发生于1983-03-07，位于甘肃省东乡县境内巴谢河北岸，以实例中洒勒山新滑坡的位移监测资料1985年3月～12月共10个月的监测数据建立滑坡预测模型。运用本文所介绍的模糊时间序列模型的预测步骤，对1985年8月～12月的数据进行预测，并将预测结果与指数模型、Verhulst模型和灰色GM(1，1)模型的预测结果进行了比较，结果见表1。

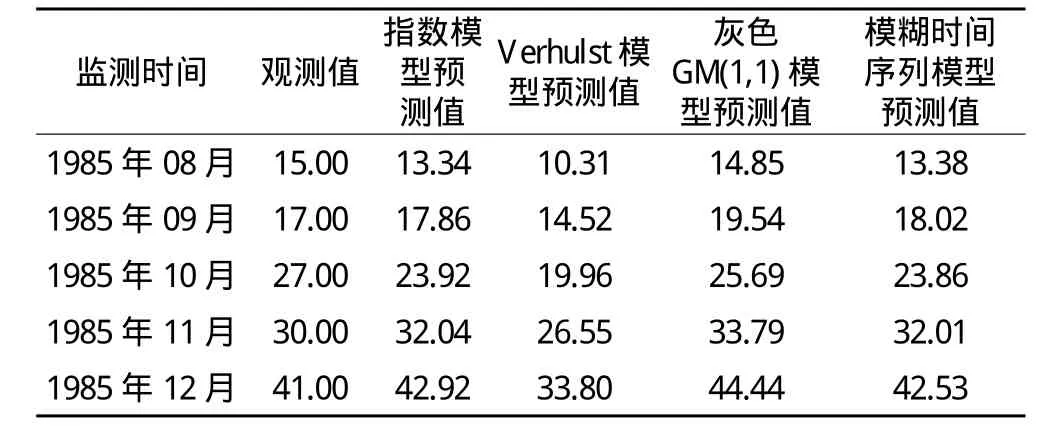
表1 各模型预测结果表/cm

本文采用均方误差（MSE）和平均绝对百分误差（MAPE）来衡量模型的精度。设观测值为yi，预测值为，则均方误差和平均绝对百分误差分别为：

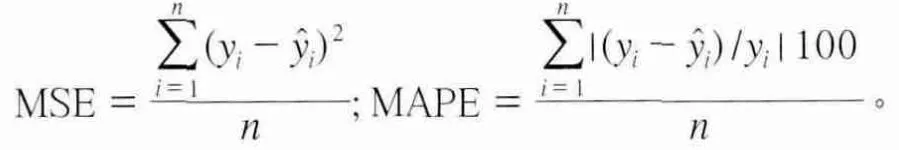
4种模型的精度评定结果见表2。

从表1、表2的计算结果来看，模糊时间序列模型预报的精度略优于其他3种模型，均方误差、平均绝对百分误差指标相对其他模型而言都是比较好的，充分说明了模糊时间序列预报模型具有比较优良的性能，可用于滑坡预报。

表2 各模型精度评定表

3 结 语

模糊时间序列模型建模简单，所需样本数据较少，且计算简单，使用方便，短期预报精度较高。由于模糊时间序列预测方法是一门新兴的研究领域，如何客观地划分论域区间、确定隶属函数、构建合适的模糊规则以及去模糊化方法仍然是影响模型预测精度的关键因素。进一步改进建模过程，提高预测精度以及更深入地应用到滑坡预测预报中，将是下一步要做的工作。

[1]Song Q, Chissom B S.Fuzzy Time Series and Its Models [J].Fuzzy Sets System, 1993, 54(3): 269-277

[2]Song Q, Chissom B S. Forecasting Enrollments with Fuzzy Time Series[J].Part 1. Fuzzy Sets System, 1993, 54(1):1-9

[3]Song Q, Chissom B S. Forecasting Enrollments with fuzzy time series[J].part 2. Fuzzy Sets System, 1994, 62(1):1-8

[4]Chen S M, Hwang J R. Temperature Pprediction using Fuzzy Time Series [J]. IEEE Transactions Systems Man Cybernetics Part B: Cybernetics, 2000, 30(2):263-275

[5]Sun X H, Li Y M. Average-based Fuzzy Time Series Models for Forecasting Shanghai Compound Index [J]. World Journal of Modeling and Simulation,2008, 4: 104-111

[6]Tsaur R C, Kuo T C. The Adaptive Fuzzy Time Series Model with An Application to Taiwan's Tourism Demand [J]. Expert Systems with Applications, 2011, 38:9 164-9 171

[7]倪明.模糊时间序列预测模型研究及其在污水处理上的应用[D].成都:西南石油大学，2012

[8]王永弟. 模糊时间序列模型在短期气候预测中的应用[J].南京信息工程大学学报：自然科学版，2012，4(4) : 316-320

[9]陈刚，曲宏巍.一种新的模糊时间序列模型的预测方法[J].控制与决策，2013，28(1):105-108

[10]李秀珍，王成华，孔纪名.基于最优加权组合模型及高斯—牛顿法的滑坡变形预测研究[J].工程地质学报，2009，17(4)：538-543