F-P腔不同扫频段透射谱锁频精度实验
安盼龙,郑永秋,李小枫,张建辉,段美玲,薛晨阳,闫树斌
(1.中北大学 仪器科学与动态测试教育部重点实验室, 山西 太原 030051;2. 中北大学 电子测试技术重点实验室, 山西 太原 030051; 3.中北大学 理学院,山西 太原 030051)
引言
法布里-波罗干涉仪(Fabry-Parot, F-P)是一种精密的光学仪器,由于其透射谱线半高全宽(full width at half maximum, FWHM)很窄,广泛应用于激光器谐振腔、精细距离的测定、信号的检测分析等[1-2]。对于光纤陀螺的锁频研究也是近年来惯性导航领域关注的焦点,光纤陀螺分为干涉型(interferometric fiber optic gyroscope, I-FOG)和谐振型(resonator fiber optic gyroscope, R-FOG)两类,其中谐振式陀螺的核心敏感单元光纤环腔的透射谱线所对应的半高全宽(FWHM)较窄,品质因数Q值高达107,故常利用F-P腔的更窄线宽、高精细度特性来对其锁频并反馈至激光器,使激光器频率变化跟踪环形腔的变化[3-5]。设计光路,对F-P腔使用比例-积分控制电路(proportion integration,PI)进行锁频实验,比较不同激光器扫频段得到的锁频曲线,并计算其锁频精度,为后续开展光纤环腔陀螺的锁频输出测试提供实验指导。
1 F-P腔干涉原理图
F-P干涉仪(图1)主要由2块平行放置的平面板所组成,在2个板相向的平面G和G′上镀有薄银膜或其他反射率较高的薄膜,要求镀膜的平面与标准样板之间的偏差不超过1/50~1/20波长。若两平行的镀银平面的间隔固定不变,则该仪器称为法布里-珀罗标准具。面光源S放在透镜L1的焦平面上,使许多方向不同的平行光束入射到干涉仪上,在GG′间作来回多次的反射,最后透射出来的平行光束在第二透镜L2的焦平面上形成同心圆形的等倾干涉条纹[6]。

图1 F-P腔干涉原理图Fig.1 Principle diagram of F-P cavity interference
当G、G′面的反射率很大时,由G′透射出来的各光束的振幅基本相等,这接近于等振幅的多光束干涉[7]。计算这些光束的叠加结果,合振幅A可用下式表示[8]:
(1)
式中:A0为每束光的振幅;N为光束的总数;φ则为各相邻光束之间的位相差。
2 F-P腔锁频原理
图2为F-P腔透射谱以及鉴频曲线,从图2可以看出该解调曲线在谐振频率点处幅值为零,随着谐振频率的偏离,解调曲线在一定谐振频率差范围内保持线性变化。将解调曲线作为扫描激光器压电陶瓷(PZT)的误差信号输入给PI反馈控制电路来进行谐振频率的跟踪和锁定的[9-11]。当输入光源的频率开始进入谐振峰时,由于产生的这种误差信号经PI反馈控制电路后改变PZT扫描电压,使这种误差信号减小,只要有误差信号,这种反馈控制作用就一直进行,结果使误差信号为零,此时的光源频率也被锁定在谐振频率点处。当腔体谐振频率在外界环境影响下漂移时,扫描激光器PZT的电压随之变化,通过测量该电压的变化可以得到谐振频率的变化量,从而可以评估外界环境参数的变化量。

图2 F-P腔透射谱和解调曲线Fig.2 F-P cavity transmission spectrum and demodulation curve
3 测试系统
图3为测试系统光路设计原理图,波长为1 550 nm窄线宽激光器(<1 kHz)发出的光经Thorlabs公司型号为LN65S铌酸锂带宽为10 GHz相位调制器,使用信号发生器1产生正弦波对相位调制器进行调制,信号发生器1型号为斯坦福Model DS345,可产生正弦波、方波、锯齿波、三角波等多种波形,最高频率可达30 MHz;另使用信号发生器对比例积分模块进行扫描,扫描电压和频率分别为1 V和20 Hz。激光经过准直输出至2个与激光器光轴成45°平行放置的三维可调节全反平面镜,然后进入法布里-波罗标准具,调节激光使其输出高度与F-P腔保持一致,并且与腔轴平行,空间光从F-P腔经过多次反射干涉空间输出至New Focus公司可调光电探测器Model 2053,其带宽为10 MHz,最大转换增益为18.8×106V/W,调节光电探测器接收空间光至示波器屏幕上得到最大探测值。锁相放大器为斯坦福SR844型号,检测范围为25 kHz~200 MHz; PI是由基本运放电路构建的,主要通过调节电路中的电阻及电容值来实现反馈控制。高压放大器为山大宇光YG2009A HV DC Amp(direct-current high voltage amplifier,HV),其功能是放大信号电压对PZT(piezoelectric transducer)进行扫描,电压放大范围:0~350 V,激光器PZT扫描电压范围:0~200 V。

图3 系统搭建原理图Fig.3 Principle diagram of system setup
4 锁频实验
采用高压直流放大器对激光器输出电压由小到大顺序进行数字扫频,高压放大器最高扫频电压350 V,而激光器PZT承受最大电压为200 V,故经过扫频得到了4次不同的F-P腔的谐振干涉透射谱线,经过4次分别解调,得到透射谱所对应的鉴频曲线,根据标准偏差的公式对数据进行处理:
(2)
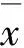
另由Allan方差的定义,设采样时间为τ0,共采样N个点,本测试采样点N=10 000个,并且把所采集的N个数据分成K组,本测试K=10组,每一个采样点记为Xi,每组包括M(M≤(N-1)/2)个采样点,则M=1 000,每组的持续时间τM=Mτ0称为相关时间,算出每一组均值:
(3)
则安伦方差最后表示为
(4)
Allan方差反映了相邻2个采样段内平均频率差的起伏,最后经处理得到了4组不同锁频精度值。
4.1 扫频参数1
表1给出了各仪器第1种锁频参数设置情况,即在此参数下实施锁频。

表1 各测试仪器锁频参数设置Table 1 Parameters of each tested instrument for frequency locking
图4(a)为锁频电压波动与采样时间关系曲线图,图4(b)利用鉴频曲线与直流高压放大器的扫频常量15 MHz/V进行局部放大测试。锁频后电压波动ΔV=0.013 8 V,如图4(a)所示。正弦波压差ΔV=0.003 4 V,如图4(b)所示。本次数据采样时间100 ms,采样点10 000,经过统计计算标准偏差为0.002 242 7,Allan方差为1.419 83×10-7,锁频精度为2.07 MHz。
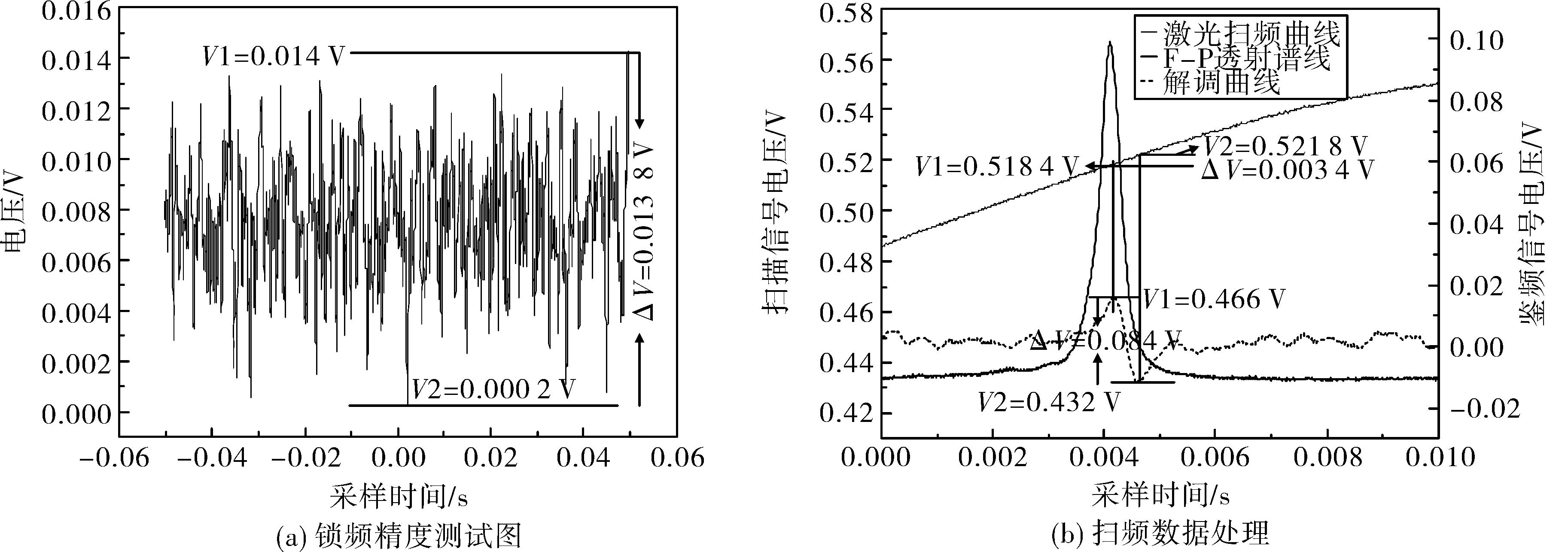
图4 HV为58 V锁频精度测试与数据处理Fig.4 Locked precision testing and data processing when HV is 58 V
4.2 扫频参数2
表2给出了各仪器第二种锁频参数设置情况,即在此参数下实施锁频。
图5(a)为另一采样时段锁频电压波动与时间关系曲线图,图5(b)同样为利用鉴频曲线与直流高压放大器输出监控的正弦曲线,其激光器PZT扫频常量为15 MHz/V。锁频后电压波动ΔV=0.01 V,如图5(a)。进行局部放大测试,找到正弦波压差为ΔV=0.003 V,如图5(b)。本次数据采样时间100 ms,采样点10 K,经过统计计算,其标准偏差为0.001 577 6,Allan方差为4.201 89×10-8,锁频精度为1.50 MHz。

表2 各测试仪器锁频参数设置Table 2 Parameters of each tested instrument for frequency locking

图5 HV为73 V锁频精度测试与数据处理Fig.5 Locked precision testing and data processing when HV is 73 V
4.3 扫频参数3
表3给出了各仪器第3种锁频参数设置情况,即在此参数下实施锁频。
图6(a)为另一采样时段锁频电压波动与时间关系曲线图,图6(b)同样为利用鉴频曲线与直流高压放大器输出监控的正弦曲线,其激光器PZT扫频常量为15 MHz/V。锁频后电压波动ΔV=0.011 5 V,如图6(a)。进行局部放大测试,找到正弦波压差为ΔV=0.002 8 V,如图6(b)。本次数据采样时间100 ms,采样点10 K,经过统计计算,其标准偏差为0.001 901 3, Allan方差为2.448 1×10-7,锁频精度2.055 MHz。

表3 各测试仪器锁频参数设置Table 3 Parameters of each tested instrument for frequency locking
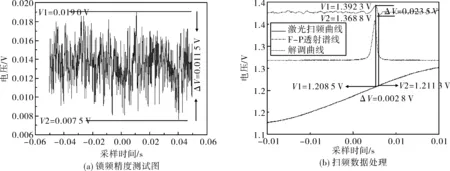
图6 HV为131 V锁频精度测试与数据处理Fig.6 Locked precision testing and data processing when HV is 131 V
4.4 扫频参数4
表4给出了各仪器第4种锁频参数设置情况,即在此参数下实施锁频。
图7(a)为另一采样时段锁频电压波动与时间关系曲线图,图7(b)同样为利用鉴频曲线与直流高压放大器输出监控的正弦曲线,其激光器PZT扫频常量为15 MHz/V。锁频后电压波动ΔV=0.011 V,如图7(a)。进行局部放大测试,找到正弦波压差为ΔV=0.004 V,如图7(b)。本次数据采样时间100 ms,采样点10 K,经过统计计算,其标准偏差为0.001 961 7,Allan方差为7.605 39×10-7,锁频精度2.13 MHz。

表4 各测试仪器锁频参数设置Table 4 Parameters of each tested instrument for frequency locking

图7 HV为186 V锁频精度测试与数据处理Fig.7 Locked precision testing and data processing when HV is 186 V
5 结果比较
图8(a)为锁频精度对应的直流高压值关系曲线,图8(b)为安伦方差对应的直流扫频电压关系图。经过比较4测试结果发现,当直流高压放大器扫频电压为73 V时,所得到的锁频精度、标准方差和Allan方差最小,锁频效果最好。
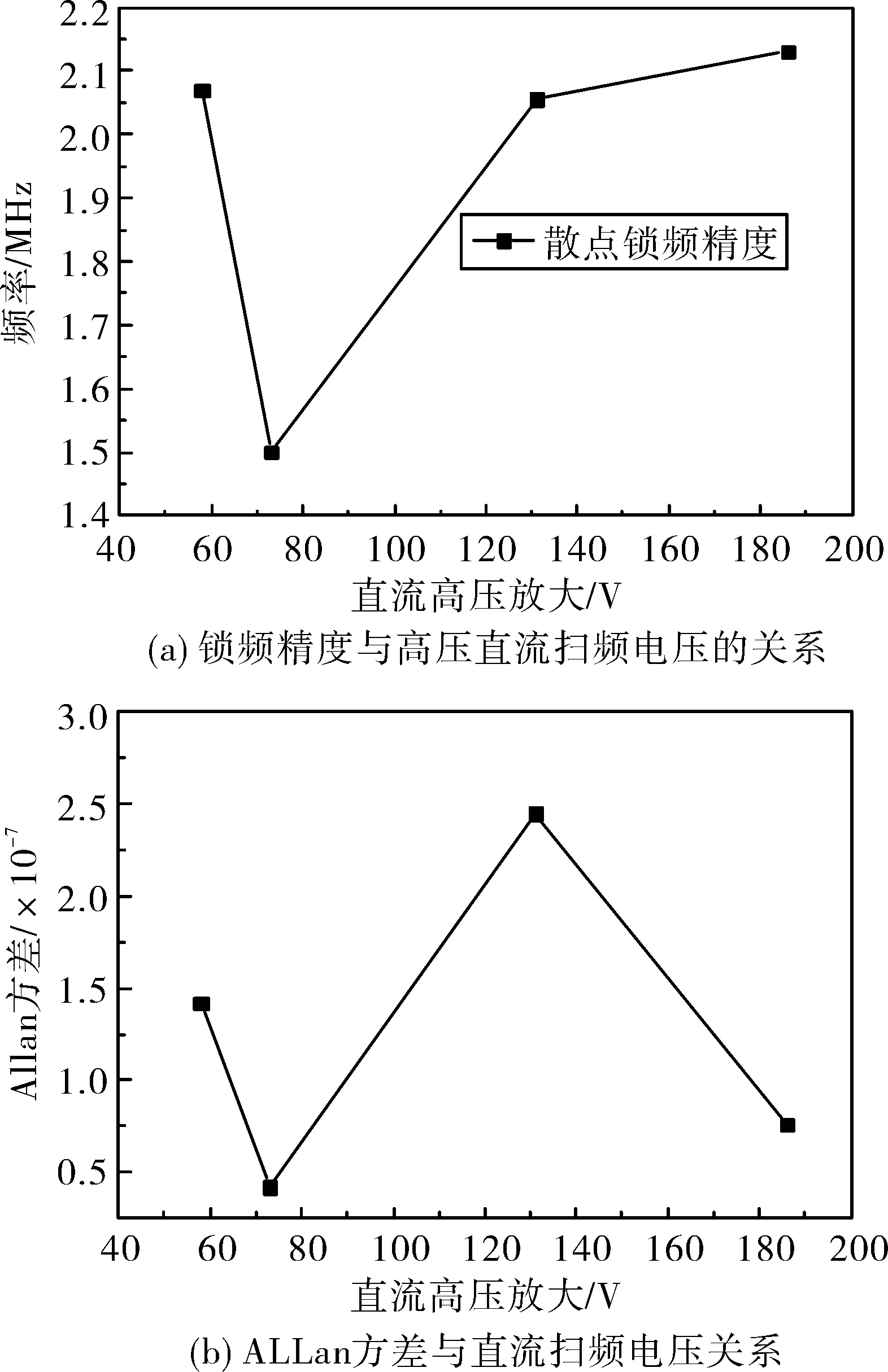
图8 F-P腔锁频效果比较Fig.8 Comparison of F-P cavity locked frequency effect
6 结束语
通过设计共焦球面F-P腔锁频光路,运用PI电路对腔其实施锁频,使激光器的频谱被压窄到一个很小的范围,锁频精度达到1.5 MHz,标准偏差为0.001 58,Allan方差为4.20×10-8。由结果分析可知,使用相同电压和频率对F-P腔进行调制,不同直流电压对激光器的PZT进行扫频,锁定后精度并不一样,且精度差别较大。从4种扫频结果可以看出,窄线宽光纤激光器(1 kHz)的最佳状态处于73 V左右,这时的PZT接收反馈工作状态最佳,锁频精度和Allan方差的值最小。
[1] Lu Hong, Jiang Lingzhen, Geng Wanzhen,et al. Study on the real time measurement of passive incident laser wavelength with F-P interferometers [J].Journal of Applied Optics, 1996, 17(1): 18-22.
陆宏,姜铃珍,耿完祯,等.利用F-P标准具组实时测量被动入射激光波长[J].应用光学,1996, 17(1): 18-22.
[2] Ding Hongsheng, Tong Lige, Yin Hong, et al. Methods to improve the sensitivity and stability of CFPI for surface ultrosonic vibration detection [J]. Journal of University of Science and Technology Beijing,2001,23(5):445-448.
丁红胜,童莉葛,尹红,等.共焦法布里-珀罗干涉仪灵敏度和稳定性研究[J].北京科技大学学报,2001,23(5):445-448.
[3] Yang Haijing,Wang Yanhua,Zhang Tiancai et al. Modulation-free frequency stabilization of a laser based on a confocal Fabry-Perot cavity[J].Chinese J. Lasers,2006,33(3):316-320.
杨海菁,王彦华,张天才,等.基于共焦法布里-珀罗腔的无调制激光频率锁定[J]. 中国激光,2006,33(3): 316-320.
[4] Li Jian, Wu Lingan. Phase modulation locked optical resonator [J].Acta Optica Sinica,1995, 15(12):1641-1645.
李健,吴令安.相位调制锁定光学谐振腔[J].光学学报,1995,15(12):1641-1645.
[5] Hong Lingfei, Zhang Chunxi, Feng Lishuang, et al. Frequency tracking and locking methods in resonator mirco-optic gyro [J]. Chinese Journal of Laser,2011,38(9): 0905009-1-1105004-5.
洪灵菲,张春熹,冯丽爽,等. 谐振式微光学陀螺频率跟踪与锁定技术研究[J].中国激光,2011,38(9):0905003-1-5.
[6] Ma Baohong,Zhang Zhanjie.The analysis of Fabry-Perot’s principle and application[J].Journal of Luoyang Normal University, 2012,31(11):29-33.
马宝红,张战杰.法布里珀罗干涉仪原理及应用分析[J].洛阳师范学院学报,2012,31(11):29-33.
[7] Lu Honggang, Jiang Yanyi, Bi Zhiyi. Measurement of reflectivity of optical mirrors using laser phase modulation and fineness of Fabry-Prot cavity[J]. Chin. J. Lasers,2006, 33( 12 ):1675 -1679.
鲁红刚,蒋燕义,毕志毅.激光相位调制法布里-珀罗腔精细度法测定反射率[J].中国激光,2006,33(12): 1675-1679.
[8] Yao Qijun. Optical tutorial [M].Beijing: Higher Education Press,2002.
姚启钧.光学教程[M].北京: 高等教育出版社,2002.
[9] Black E D. An introduction to pound-drever-hall laser frequency stabilization [J]. Am. J. Phys.,2001, 69(1):79-87.
[10] Sun Xutao, Chen Weibiao. Optimization of pound-drever-hall frequency stabilization of injection-locked laser [J]. Acta Photonica Sinica, 2008, 37(9): 1748-1752.
孙旭涛,陈卫标.注入锁定激光器的边带锁频技术稳频系统优化分析[J].光子学报,2008,37(9):1748-1752.
[11] Yan Shubin, Wang Yanhua, Liu Tao,et al. Modulation-free laser frequency locking by AOM shifted cesium sub-Doppler spectra[J]. Acta Optica Sinica, 2004, 24(10): 1335-1338.
闫树斌,王彦华,刘涛,等.声光偏频亚多普勒光谱无调制激光频率锁定[J].光学学报, 2004, 24 (10):1335-1338.

