一类非线性自治Liu系统的Hopf分岔分析

李耀伟，张 莉，杨 敏

(1.兰州交通大学 数理学院，甘肃 兰州 730070;2.兰州工业学院 基础学科部,甘肃 兰州 730050)

1963年,气象学家Lorenz首次在一个三维自治系统中发现了混沌吸引子[1].近年以来,学者们在认识、研究混沌理论及其应用的过程中,各种各样的非线性混沌系统也相继被提出,如Chen系统[2],Liu系统[3],Chu系统[4]等等,使得它们在数学、物理及其工程实际应用中得到了极大的发展,并且得到了各界学者的广泛研究.考虑到非线性系统有很好的价值以及许多复杂的动力学行为,许多新的非线性系统也被相继提出[5-7].对于一类由Liu等[8]提出的Liu系统，他们研究了该系统实现混沌的机制，而有关该系统的分岔行为还没有被研究过，本文基于第一李雅普诺夫系数法研究了系统平衡点稳定性及其Hopf分岔.通过计算第一李雅普诺夫系数，从而分析了该系统Hopf分岔的方向以及参数条件.最后对该系统进行了数值仿真，验证了理论推导的正确性.

1 新的Liu系统模型

文献[8]提出了一个新的具有混沌状态的非线性系统,其状态方程为：

(1)

其中a,b,c为实常数,当a=10,b=40,c=2.5时系统存在一个混沌吸引子.如图1(a)所示,系统(1)的时间响应图、Poincare截面图、李雅普诺夫指数谱图, 如图1(b),(c),(d)所示.

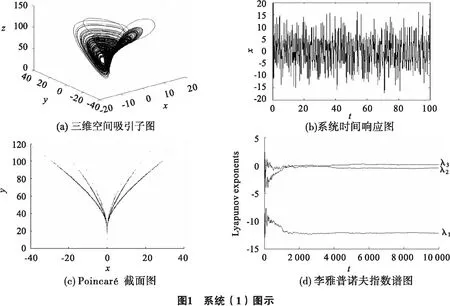
2 局部稳定性与Hopf分岔存在性分析

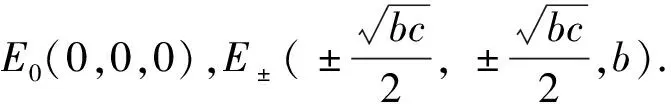
2.1 平衡点E0

系统(1)在(x,y,z)处的李雅普诺夫矩阵为:

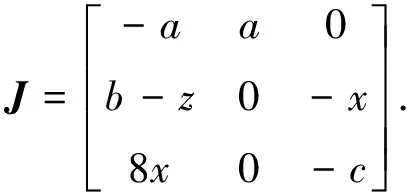
(2)

系统(1)在平衡点E0(0,0,0)处的特征多项式是(λ+c)(λ2+aλ-ab)=0.则上式有根为λ1=-c,由方程λ2+aλ-ab=0 可以求得方程的另外2个根λ2,λ3.

根据Routh-Hurwitz判据知方程的一切根的实部为负数的必要且充分条件是:

(3)

由上可知a>0,b<0,c>0.

命题1 当a>0,b<0,c>0时，平衡点E0(0,0,0)渐近稳定.

推论1 当c<0时，平衡点E0(0,0,0)不稳定.

推论2 当c变为固定值c=0时，一个特征值变为0，系统出现pitchfork分岔，由平衡点E0(0,0,0)处雅可比矩阵的特征方程(λ+c)(λ2+aλ-ab)=0,易知,随着参数a,b,c的变化,特征方程只会出现零根,而始终无纯虚根,故平衡点E0(0,0,0)不会发生Hopf分岔．

2.2 平衡点E+

系统(1)在平衡点E+的雅可比矩阵为

(4)

则系统(1)在E+处的李雅普诺夫特征多项式为:

λ3+(a+c)λ2+acλ+2abc=0.

(5)

根据Routh-Hurwitz判别条件,知方程(5)的一切根的实部为负数的必要且充分条件是下列不等式成立:

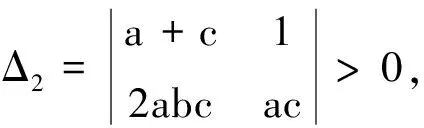
(6)

由(6)式可以得出a+c>0,abc>0,ac(a+c-2b)>0.而bc>0时平衡点E1存在.

命题2 当bc>0,a>0,a+c>0,ac(a+c-2b)>0时,平衡点E+渐近稳定.

同理可证明当bc>0,a>0,a+c>0,ac(a+c-2b)>0时平衡点E-渐近稳定.

证明设平衡点E+雅可比矩阵的特征多项式(5)有一对共轭的纯虚根λ1,2=±wi(w>0),多项式的另一实根为λ3=-(a+c),将λ1,2带入(5)可得：

-w3i-(a+c)w+acwi+2abc=0.

(7)

(7)式为0的充要条件是实部与虚部都为0,分离实部与虚部有：

(8)

从(8)式可以解得：

(9)

经计算可得：

(10)

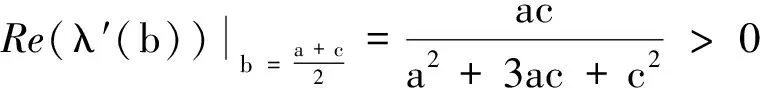
3 平衡点E1处的超临界与亚临界Hopf分岔分析

运用第一李雅普诺夫系数法讨论系统的超临界与压临界Hopf分岔,在理论分析之前,先回顾一下文献[4-5]中介绍的Hopf分岔的第一、二李雅普诺夫系数的求法.

考虑如下系统

x′=f(x,ζ).

(11)

其中x∈R3,ζ∈R3分别是系统的状态变量和控制参数;假设系统(11)有一个平衡点x=x0,ζ=ζ0,并且变量x-x0仍然记做x,则F(x)=f(x,ζ0)的泰勒展开式为

(12)

其中A=fx(0,ζ0),并且对i=1,2,3有

(13)

假设在平衡点(x0,ζ0)，系统(11)的雅可比矩阵有一对纯虚根λ2,3=±iω0,(ω0>0),并且其它的特征值没有零实部,令Tc为λ2,3的特征向量所产生的空间.

令p,q∈C3满足

(14)

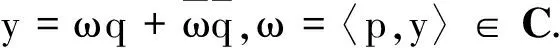
(15)

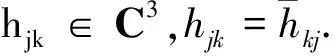
(16)

其中F见(12)式.可以通过解(16)求得hjk,(16)可以在ω上写成如下中心流型

其中Gjk∈C.则第一李雅普诺夫系数可以定义为

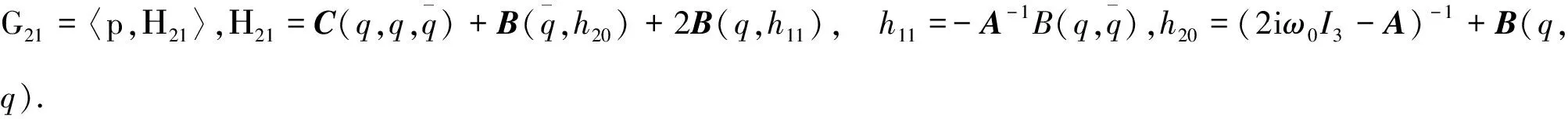
如果系统的一个平衡点为Hopf分岔点,则在此平衡点处的雅可比矩阵A有一对纯虚根λ2,3=±iω0(ω0>0),且其它的特征值Reλ1≠0.若此时平衡点满足橫截性条件,并且l1≠0则发生余维一的Hopf分岔.当l1<0时,平衡点E0渐进稳定,发生超临界的Hopf分岔;当l1>0时,平衡点E0不稳定,发生亚临界的Hopf分岔. 当l1=0,则原系统(1)在平衡点E1处发生余维二的退化Hopf分岔．

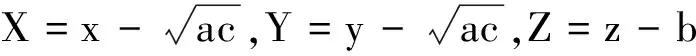
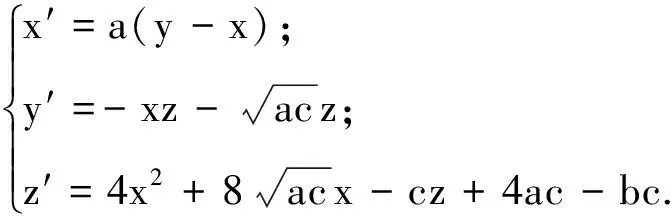
由上述的理论分析可以计算得：p=(p1,p2,p3),q=(q1,q2,q3).

其中

并且有Aq=iq,ATp=-ip,〈p,q〉=p1q1+p2q2+p3q3=1,

根据基础理论部分通过计算可得：

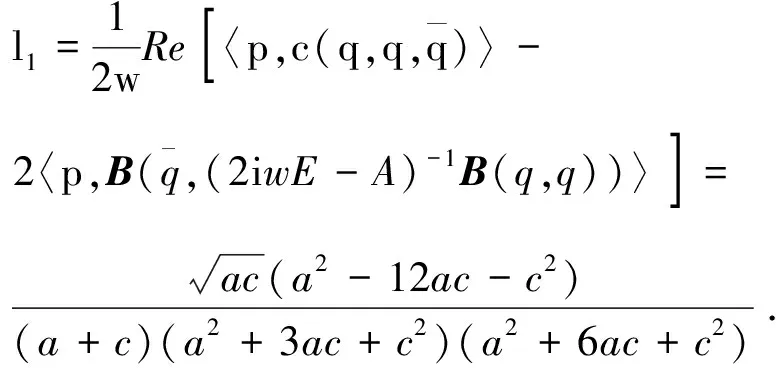
故得到如下的定理.

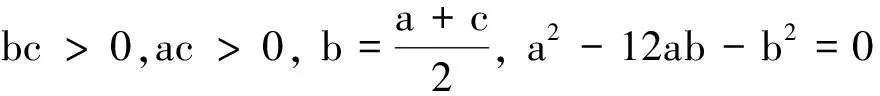
4 数值仿真

为了验证以上的理论分析,我们选取一组参数:a=4，c=2,可以得到Hopf的临界值b0=3.当bb0时,系统的相图分别如图2(a),(b)和(c)所示.

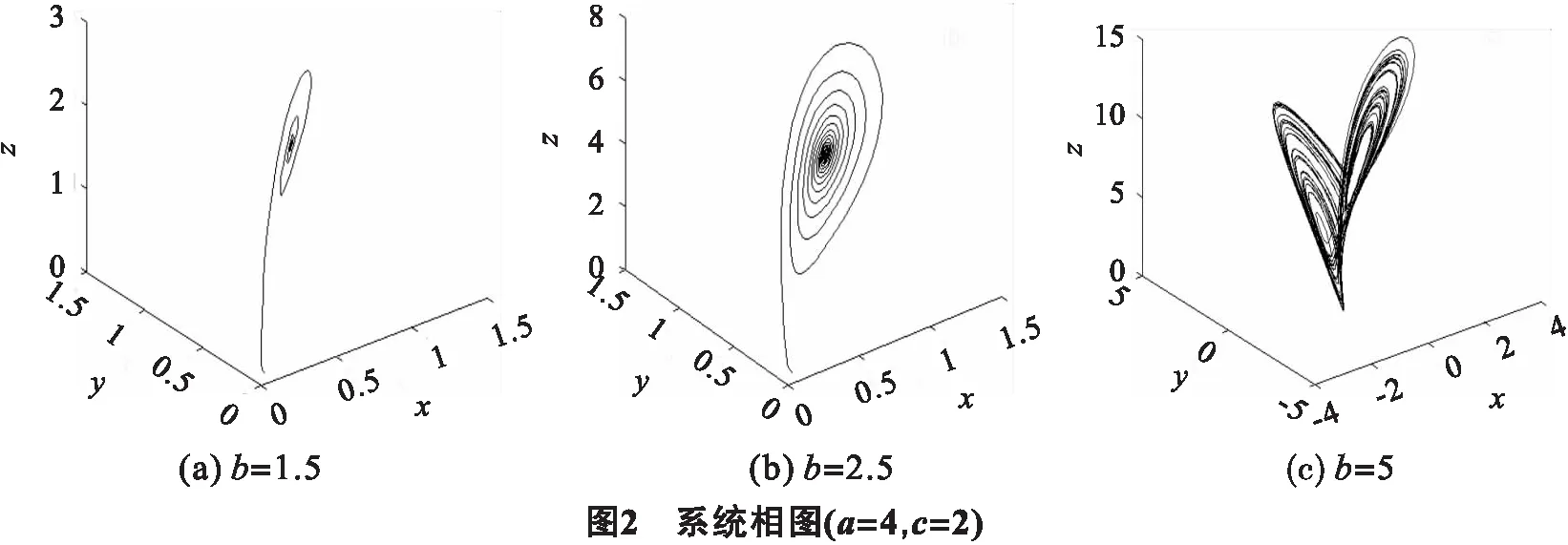
进而给出图3所示分岔图，当b=3时分岔图明显变粗，系统此时发生Hopf分岔,如图3,因而数值仿真于理论分析一致．

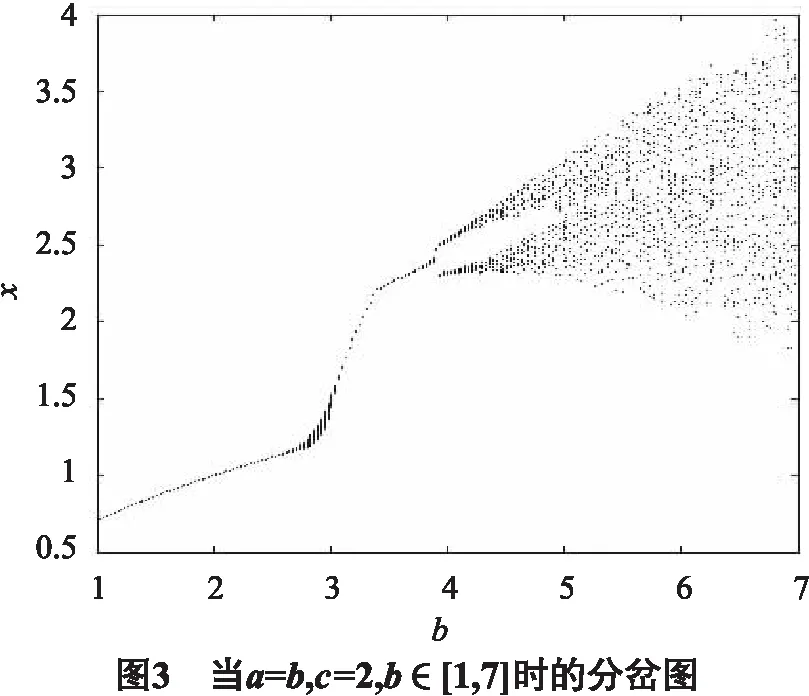
5 结语

本文主要研究了一个新的Liu系统的Hopf分岔特性.通过选取适当的分岔参数,证明了当分岔参数经过临界值时系统发生了Hopf分岔.并且详细分析了发生超临界与亚临界分岔的参数条件.并运用数值仿真验证了理论推导的正确性．尽管系统简单,但它有着十分丰富的动力学特性.虽然本文进行了详细的研究,但是系统混沌吸引子的形成机理需要进一步的分析, 其拓扑结构也应该彻底地研究.因此,对系统的进一步研究仍然是重要和有意义的.

参考文献:

[1] LORENZ E N. Deterministic nonperiodic flow[J]. Journal of the Atmospheric Sciences, 1963, 20(2): 130-141.

[2] CHEN G, UETA T. Yet another chaotic attractor[J]. International Journal of Bifurcation and Chaos, 1999, 9(07): 1465-1466.

[3] LYU J, CHEN G. A new chaotic attractor coined[J]. International Journal of Bifurcation and Chaos, 2002, 12(03): 659-661.

[4] DIAS F S, MELLO L F, ZHANG J G. Nonlinear analysis in a Lorenz-like system[J]. Nonlinear Analysis: Real World Applications, 2010, 11(5): 3491-3500.

[5] CHU Y, LI X, ZHANG J, et al. Nonlinear dynamics analysis of a new autonomous chaotic system[J]. Journal of Zhejiang University SCIENCE A, 2007, 8(9): 1408-1413.

[6] YUJUN N, XINGYUAN W, MINGJUN W, et al. A new hyperchaotic system and its circuit implementation[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(11): 3518-3524.

[7] WANG X, WANG M. A hyperchaos generated from Lorenz system[J]. Physica A: Statistical Mechanics and its Applications, 2008, 387(14): 3751-3758.

[8] LIU C, LIU T, LIU L, et al. A new chaotic attractor[J]. Chaos, Solitons and Fractals, 2004, 22(5): 1031-1038.

[9] LIU M, FENG J, TSE C K. A new hyperchaotic system and its circuit implementation[J]. International Journal of Bifurcation and Chaos, 2010, 20(04): 1201-1208.

[10] 杜文举,俞建宁,安新磊,等.一个新的四翼混沌系统的动力学分析[J].云南民族大学学报:自然科学版,2013,22( 4):275-279.

[11] 张文，刘海鸿，张健. 一类关于Leslie-Gower捕食-被捕食时滞模型的局部Hopf分岔分析[J].云南师范大学学报：自然科学版，2012，32(1)：42-47.