相似直角三角形在电工基础中的运用

（陕西榆林职业技术学院，陕西 榆林 719000）

相似直角三角形在电工基础中的运用

刘 钰

（陕西榆林职业技术学院，陕西 榆林 719000）

首先简述了直角三角形的勾股定理，通过对交流电路中阻抗、电压、功率直角三角形的分析，并阐明在同一电路中，三组三角形具有相似性，通过例题分析了利用相似性，可以较为简便地对电工电路中各参数进行计算。

直角三角形；相似；阻抗；电压；功率；电工基础；运用

直角三角形的主要特性之一是勾股定理，即斜边的平方等于两直角边的平方和。而电工基础是一门理论性较强的专业基础课，特别是交流电路，电路中电压、电流等参数既有大小，又有方向，同时，在交流电路中阻碍电流的物理量除了电阻以外，还有电感、电容。这使得我们在计算时需要考虑多种因素，一旦考虑不周，很容易出错，如果在计算交流电路各参数时，能够使用相似直角三角形的特性，那就容易多了。下面以对单相感性交流电路来分析。

一、阻抗直角三角形

在交流电路中，阻碍交流电路的物理量除了耗能元件电阻以外，还有储能元件电感和电容。电阻的大小与电路中的频率无关，而电感和电容对交流电的阻碍作用与频率有关。我们把电感对交流电的阻碍作用称为感抗，即频率越大，阻碍作用越大，即具有“通直抑交”的作用。电容对交流电的阻碍作用称为容抗，即频率越大，阻碍作用反而减小，即具有“通交抑直”的作用。如果在同一电路中既有电阻，又有电感和电容，可以通过直角三角形，即阻抗直角三角形来分析整个电路的阻碍作用，如图（1）。图中一直角边为电阻R，另一直角边为电抗X（X=XL-XC），斜边为阻抗|Z|，从图中可知阻

二、电压直角三角形

在交流电路中，总电压可能小于其中一元件的电压，如图（2）为电压直角三角形，总电压为U，即直角三角形的斜边，电阻元件的电压为UR，一直角边，另一直角边为UL-UC。其中电阻元件的电压与电流同相，电感元件两端电压超前电流900，电容元件两端电压滞后电流900。图中各电压具有的关系为

三、功率直角三角形

在交流电路中，除了有功功率外，还有无功功率和视在功率。同样三个功率也可以构成直角三角形，如图（3），其中斜边为视在功率（S=UI），一直角边为有功功率P（P=UIcosφ）,另一直角边为无功功率Q（Q=UIsinφ），三功率也满足

（1）阻抗直角三角形（2）电压直角三角形（3）功率直角三角形

四、三个直角三角形在计算中的运用

在同一电路中，上述电压、功率、阻抗直角三角形为相似三角形，即Φ1=Φ2=Φ3.在实际计算中利用三角形的相似特性，就可以比较容易地计算出交流电路中地参数，下面通过一道例题来分析。

例题：一电阻、电感、电容串联的单相交流电路，若电阻R=60Ω,电阻两端的电压UR为60V，电抗X的电压UX为80V,有功功率P为30KW。

求：端电压U、阻抗|Z|、无功功率Q、视在功率S及功率因数cosφ。

解：根据电压直角三角形可得，

端电压：

可得：无功功率

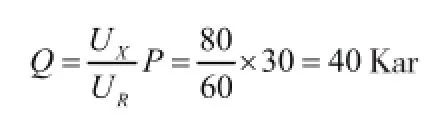
在电工基础中，要计算电压，功率，一般需要先计算电流，再利用公式计算所需量。而这道题，我们仅仅利用三角形的相似特性，较为简单地就算出了我们需要计算的量。可以看出，在学习交流电路中，如果我们能够很好地把直角三角形及三角形地形似特性运用在计算中，就可以减少好多繁琐地过程，较为简便地计算出电路中对应地参数。

[1]钱丽丽．一道解直角三角形典型题的解析[J]．新课程（上）,2011（05）．

G634

A