轮对组装的压装力曲线自动判断数学模型研究
杜宏光 姜 斌 裴 鹏 鲍明全 范 玮
(唐山轨道客车有限责任公司,063035,唐山市∥第一作者,教授级高级工程师)
轮对组装的压装力曲线自动判断数学模型研究
杜宏光 姜 斌 裴 鹏 鲍明全 范 玮
(唐山轨道客车有限责任公司,063035,唐山市∥第一作者,教授级高级工程师)
在TB/T 1718—2003《铁道车辆轮对组装技术条件》中,对车轮压装力曲线以文字及图例的方式作出了具体规定。根据该标准中的规定,就如何建立数学模型,实现轮对压装机的压装力曲线自动判断进行了研究,可为完善铁路标准、优化自动判断程序提供借鉴。
铁道车辆;轮对组装;压力曲线;自动判断;数学模型
First-author'saddressTangshan Railway Vehicle Co.,Ltd.,063035,Tang shan,China
轮对是铁道车辆走行部的关键部件。车轴与车轮采用过盈配合及冷压方法组装成轮对[1]。在车辆运行中,轮对受到动静载荷作用的同时,还承受制动载荷作用,因此,轮对压装质量的好坏将直接影响行车安全。对轮对压装机进行测量监控的压装力曲线是检测产品质量的重要依据[2],是鉴定轮对组装质量的唯一标准。因此,在TB/T 1718—2003《铁道车辆轮对组装技术条件》(以下简称TB/T 1718—2003)附录A的“轮对组装压装力曲线及说明”中,自图A.1至图A.20给出了9种合格的轮对组装压装力曲线图和11种不合格的轮对组装压装力曲线图,同时针对上述不同类型的压装力曲线分别进行了文字说明。TB/T 1718—2003中关于压装力曲线的规定,为判断轮对压装曲线是否合格提供了依据,对保障铁路客车行车安全发挥了重要作用。但是,在TB/T 1718—2003的压装力曲线图示例只是提供了图形化的文件,对压装曲线打印后进行人工比对较为适宜。随着压装力机自动化程度的提高,各设备生产厂商纷纷将压装力曲线自动判断功能作为技术进步的标志。而对TB/T 1718—2003中的压装力曲线图进行数字化处理、建立曲线的数学模型,是编制自动判断程序的先决条件。将这些数学模型通过计算机语言编制成自动判断程序,安装到工控机内,就可以很方便地进行压装力曲线是否合格的判断。本文对几种典型压装力曲线的模型建立进行了研究。鉴于不同的设备制造商对计算机自动判断林林总总,不尽相同,因此,本文的研究可为完善相关铁路标准、优化自动判断程序提供借鉴。
1 压装力曲线模型的建立
压装力曲线模型建立的依据,就是TB/T 1718—2003的附录A中“轮对组装压装力曲线及说明”的各项规定。对于有明确数据规定或给出公式可资计算的的参数,其数学模型的建立,可以按照该规定编入计算机语言即可,这相对容易;而对于有些以图形形式表述的参数规定,需要将模糊的图形化标准,通过建立量化的数学模型或公式,以此作为用计算机语言编制自动判断程序的基础。在研究过程中,根据建立的模型编制程序后,还需要进行实际的压装,通过人工对自动判断的结果进行确认,以验证所建立的模型是否满足规范的规定。而这个过程有时需要多次的反复方可达到要求。因此,本文中有些参数的设置是通过多次实际压装及反复验证对比后得到的。有时为了验证程序的正确性,去除了人为设置的生产实践中很少出现的不合格参数,以保
证程序对TB/T 1718—2003的规定能够完全覆盖和满足。下面介绍几种比较重要模型的建立方法。
1.1 曲线最大压装力T2与最终压装力T3符合性判断数学模型
TB/T 1718—2003规定:“曲线的最高点压装力,不得大于按该轮毂孔直径计算的最大压装力数值;曲线终点的最小压装力,不得小于按该轮毂孔直径计算的最小压装力数值;轮轴组装最终压力按轮毂孔直径计算,每100 mm的压装力应符合表1的规定。”

表1 轮轴组装每100mm轮毂孔直径的最终压装力
由此可得出最大压装力T2(见图1)判断的数学模型为:
对40钢车轴
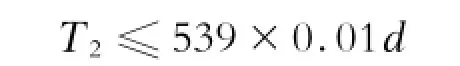
对50钢车轴

最终压装力T3(见图1)判断的数学模型为:对40钢车轴
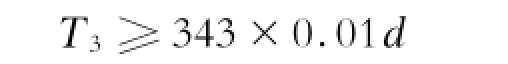
对50钢车轴

其中:d为轮毂孔直径(由实测产品获得),单位为mm;T2、T3的单位为k N。
如果采集的最大压装力和最终压装力数值同时满足上述条件,则该项指标合格;反之,该项指标不合格。针对不同材质的车轴,可在计算机程序中进行设置,操作时在窗口进行选取。

图1 车轮组装的压装力曲线示意图
1.2 曲线投影长度的数学模型
TB/T 1718—2003规定:“轮对组装压力曲线投影长度不小于理论长度的80%。”
压装力曲线理论长度L的数学计算公式为:
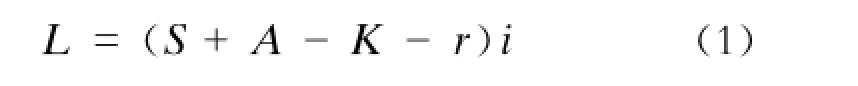
式中:
L——轮对组装的压装力曲线理论长度;
S——车轮轮毂孔长度,由设计图纸给定;
A——伸出于轮毂孔外端之轮座长度,由设计图纸给定;
K——轮座前端锥形引入段长度,由设计图纸给定;
r——车轮轮毂孔内侧之圆弧半径,由设计图纸给定;
i——压力指示器的传达系数,根据各厂压力指示器构造决定。
由式(1)即可得出L值。对于某一固定产品,因其设计图纸的有关参数已经确定,且轮轴压力机为某一固定设备时,其压装力曲线理论长度L即可计算得出,为一个常数。
压装力曲线投影长度的确定:从压装过程中采集得到的横坐标上的最大位移数据作为实际压装力曲线的投影长度,即为压装结束时对应的位移,记为压装力曲线的投影长度L0(见图1)。
压装曲线投影长度L0符合性判断的数学模型:计算L0是否满足不小于压装力曲线理论长度80%的条件,即L0≥0.8L。如果满足该条件,则该项指标合格;反之,该项指标不合格。
2 压装力曲线的判断
2.1 压装力曲线均匀上升的判断
TB/T 1718—2003规定:“压力曲线图须均匀上升。”从压装力曲线的起点到最大压装力的数据点连成一条斜线,压装力曲线需在该斜线之上。满足该条件的压装力曲线,即判断为均匀上升;否则,压装力曲线不是均匀上升。
2.2 起点陡升的判断
TB/T 1718—2003规定:“压力曲线起点陡升不超过98 k N”。
判断原始采集数据的第一点T1(见图1)的压力数据值,如果满足T1≤98 k N,则该项指标合格,否则不合格。
2.3 曲线中部下降的判断
TB/T 1718—2003规定:“压力曲线中部不应有下降。”
压装力曲线中部是压装力曲线自起始后到最大压装力之间的曲线部分。曲线中部下降的判断是对所采集的压力数据形成的压装力曲线来进行判断。一条线可以理解为由无数个点组成,反复验证表明,当组成线的各点高低的数值差不超过0.2 mm时,所形成的线用人类眼睛观察就是一条直线;当组成线的各点高低的数值差超过0.2 mm时,所形成的线用人类眼睛观察就是一条曲线。也就是说,人类对一条线是直线还是曲线的分辨率大约为0.2 mm左右。因此,把压装力曲线纵坐标方向上0.2 mm高度范围所对应压力值的大小ΔF作为判断曲线中部下降的最小分辨率指标。ΔF的计算公式为:
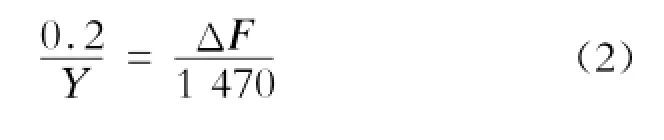
式中:
Y——压装力曲线图上压力坐标范围所对应的长度值(见图1);
ΔF——压装力曲线上最小分辨率压力值。
计算出的ΔF大约为5.45 kN。以ΔF作为指标,比较相邻两点压力差(后一点减前一点),如果超过ΔF,则判断曲线中部下降,不合格。
2.4 曲线中部平直线长度的判断
TB/T 1718—2003规定:“压力曲线中部平直线长度不得超过曲线投影长度的10%,各段平直线长度之和不得超过曲线投影长度的20%。”
影响平直线判断的因素有两个:一个是考虑平直时的压力值精度,另一个是位移方向上最小的判断长度。这两个因素的取值不同对平直线长度的确认和统计有很大的影响。经反复验证表明,以3~3.2 mm为位移方向上最小的判断长度单位。该判断长度单位前后2个点的压力数据相比较,若其相差的绝对值小于1 k N则视此段为平直段;若连续两段或更多段均为平直段,则将这些连续平直段的长度相加,记为一段L1(见图1)。L1须满足下列要求:L1≤0.1×L0满足时该项指标合格,否则不合格。如果曲线中出现多个中间平直线L1(如图1),每个L1均须符合上述要求。
将多个平直段长度进行累加得到中间平直段的总长度∑L1。则∑L1须满足下列要求:∑L1≤0.2 ×L0。满足时该项指标合格,否则不合格。
2.5 曲线末端部分平直线长度L2的判断
TB/T 1718—2003规定:“曲线末端平直线长度不得超过该曲线投影长度的15%。”
当压装力曲线一直呈上升趋势,其最高点即为曲线最终压装力数值时,不必进行曲线末端的判断,否则必须进行末端曲线的判断。曲线末端部分平直线长度L2的判断方法与曲线中部平直线长度的判断方法一样,只是L2须满足下列要求:L2≤0.15×L0。满足时该项指标合格,否则不合格。
2.6 曲线末端部分下降长度L3及下降数值情况的判断
TB/T 1718—2003规定:“曲线末端下降的长度不得超过该曲线投影长度的10%。”曲线末端下降长度L3由曲线末端总长度减去曲线末端平直长度。比较曲线末端下降长度L3是否大于曲线投影总长度的10%,即L3须满足下列要求:L3≤0.1×L0。满足时该项指标合格,否则不合格。
2.7 曲线末端部分下降平直+下降总长情况的判断
TB/T 1718—2003规定:“如曲线末端平直和下降同时存在,而压装力下降数值又不超过规定时,其合并长度不应超过该曲线投影长度的15%。”
如果压装力曲线末端同时存在平直线和下降线,则∑(L2+L3)须满足下列要求:∑(L2+L3)≤0.15×L0。满足时该项指标合格,否则不合格。
2.8 曲线末端部分下降数值情况的判断
TB/T 1718—2003规定:“曲线末端压装力的下降值不得超过按该轮毂孔直径计算的最大压力的5%。”曲线末端下降数值须满足下列要求:ΔT≤0.05 ×Tmax,满足时该项指标合格,否则不合格。
2.9 曲线中间凹下的判断
TB/T 1718—2003规定:“曲线末端压装力的下降值不得超过按该轮毂孔直径计算的最大压力的5%。”曲线开始上升的一点与Tmin的一点连成一直线(见图1),如果压装力曲线某处低于该直线,则判断曲线不合格。
3 压装过盈量超差报警
TB/T 1718—2003规定:“轮座与轮毂孔采取过盈配合,过盈量为轮座直径的0.08%~0.15%。”在车轮压装前,须将实际测量的车轴轮座尺寸和与之相配合的车轮毂孔尺寸输入到计算机内,计算机按下列公式计算出车轮压装过盈量J、理论最小过盈量Jmin和理论最大过盈量Jmax:
Mathematical Model for Automatic Judgement of Wheelset Press and Put Curves
Du Hongguang,Jiang Bin,Pei Peng,Bao Mingquan,Fan Wei
In TB/T 1718—2003"Technical Requirements of Railway Vehicle Wheelset Installation",specific press stipulations,such as the press and put curves of wheelset,the text and legends are made explicitely.According to the provisions of the standard,the establishment of a mathematical model is discussed,which will realize the automatic judgement of the press and put curves,thus providing a reference to improve railway standards and optimize the automatic judgement program.
railway vehicle;wheelset combination;press curves;automatic judgement;mathematical model
U 270.331+.1

