相控阵雷达天线模型及仿真

邱丽原

（海军航空工程学院电子信息工程系，山东烟台264001）

相控阵雷达具有波束指向灵活，可以实现无惯性快速扫描；波束形状和波束数量可控，便于进行空间滤波以及同时实现搜索、识别、跟踪、制导、无源探测等多种功能；目标容量大，对复杂目标环境的适应能力强，可在广大的空域内同时监视、跟踪多个目标，等等突出优势[1-4]。随着雷达理论、雷达技术、微电子技术、计算机技术等的深入发展，相控阵雷达已从最初的大型、地面固定、远程、战略应用，发展到今天的可以实现小型共形、机动平台、多种量程、战术应用。可以预期，相控阵雷达在现代战争中将会发挥越来越重要和广泛的作用[5-7]。

相控阵雷达的所有优势都以其天线为基础。在对相控阵雷达的理论、技术和应用研究中，对相控阵天线的建模和仿真是至关重要的。

相控阵天线的建模和仿真是一个复杂而困难的问题[8-11]：一方面，相对于其他类型的天线，相控阵天线本身就复杂并且建模困难；另一方面，在相控阵雷达工作过程中，相控阵天线产生的波束会随着其空间指向的变化而发生变化，这就要求在仿真过程中每过一个名义时间间隔（可能会短到100 μs 甚至10 μs 的量级）就要对天线波束进行一次重新计算。为了减少计算量、提高仿真速度，对于计算的复杂度提出了限制。可以认为，相控阵天线的一个好的建模和仿真应该同时满足精度高和计算复杂度低这两个通常有矛盾的要求。

本文以进行信号级的相控阵雷达作战应用仿真为目的，从相控阵天线的基本原理出发，先将相控阵天线的仿真分解为波束形状、天线增益、方向图旁瓣等3 个相对独立的部分；继而再进行综合以产生一个精度高、计算复杂度低并且灵活可控的总体仿真模型；最后，通过一个仿真实例对总体仿真模型进行了验证。

1 相控阵天线仿真的基本框架

本文中，以天线阵元（以下也简称为阵元）在平面上矩形均匀布置的相控阵天线作为研究对象，其方法可以推广到相控阵天线的其他布局类型。

相控阵天线的阵元布置及相应的阵面平面直角坐标系如图1所示：阵元数为N×M（N为x轴方向上的阵元数，M为y轴方向上的阵元数），相邻阵元间隔为dx、dy。阵面平面直角坐标系的坐标原点设置在第（0，0）个阵元处，N×M个阵元都位于xoy平面的第一象限。阵面平面直角坐标系中定义两个角度，其中的θ（θ∈[0,π 2]）为波束指向与z轴的夹角；ϕ（ϕ∈[0,2π]）为波束指向与xoz平面的夹角。

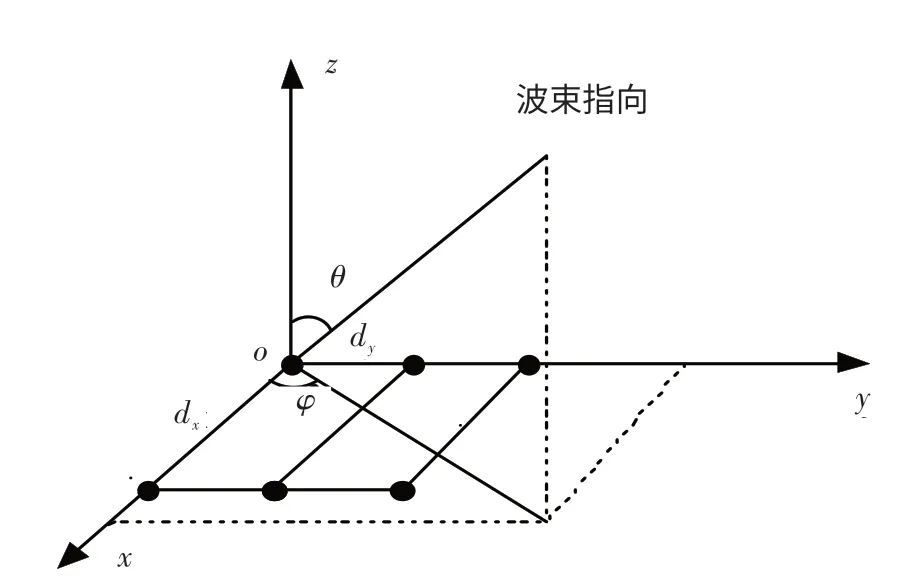
图1 阵元布置及相应的阵面平面直角坐标系Fig.1 Arrangement of array elements and corresponding array-rectangular coordinate system

1.1 相控阵天线方向图的基本描述

一般而言，相控阵天线的方向图可用下式描述[8]：

式（1）中：D(θ,ϕ) 为方向性因子；F(θ,ϕ) 为阵因子；e(θ,ϕ)为阵元因子。

以下对这3个因子分别进行分析。

1）阵元因子。对阵元的方向性通常不做要求，可以认为其全向均匀辐射，故对于阵元因子有

2）方向性因子。当波束指向(θ0,ϕ0)时，方向性因子D(θ0,ϕ0)可表示为

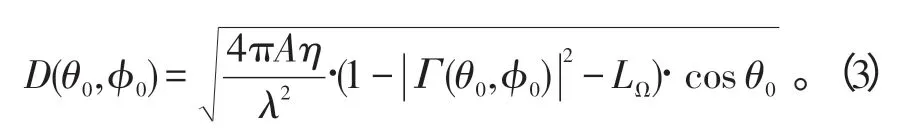
式（3）中：θ0为波束指向与z轴的夹角；ϕ0为波束指向与xoz平面的夹角；A为天线孔径面积（m2）；η为幅度加权孔径效率；为在波束中心指向(θ0,ϕ0)时的阵元失配反射系数的幅度；LΩ为波束形成网络的综合欧姆损耗。

理想情况下，幅度加权孔径效率η=1，失配反射系数和综合欧姆损耗总和。实际的相控阵雷达系统中，加权效率通常在0.6~0.8间取值，失配和综合欧姆损耗总和通常在0.4~0.7间取值。

式（3）反映的一个基本事实是，相控阵天线的增益随波束指向(θ0,ϕ0)而变。

3）阵因子。阵因子反映阵元布置对相控阵天线方向图产生的影响[12-13]。这种影响可以基于阵元布置，通过基本的远区合成电场计算直接推导出来。在图1所示的阵元布置的情况下，当波束指向(θ0,ϕ0)时，对于相控阵天线辐射的远区合成电场有[8-10]：

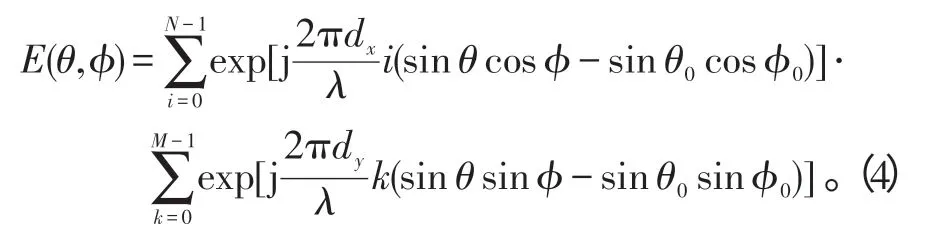
对E(θ,ϕ)化简、取模并归一化，得到：

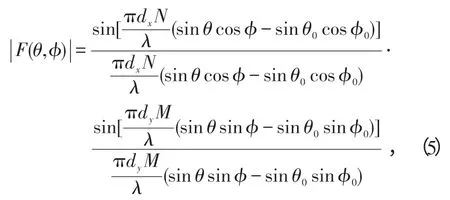
F(θ,ϕ)即为式（1）中的阵因子。

式（5）所反映的一个基本事实是，相控阵天线的波束宽度（指3dB 波束宽度，以下同）随波束指向(θ0,ϕ0)变化。设相控阵天线在波束指向阵面法线方向时的波束宽度为B0，波束指向偏离阵面法线θ0角度时的波束宽度为Bθ0，作为一阶近似结果，文献[10]有

1.2 相控阵天线方向图仿真的要点分析

基于对一般天线和相控阵天线的认识，从进行信号级的相控阵雷达作战应用仿真的目的出发，为准确、充分体现相控阵天线方向图的特点及满足仿真的精度要求，可以归纳出进行相控阵天线方向图仿真的以下要点。

对相控阵天线方向图的仿真：

1）要准确反映波束宽度，特别是不同的天线指向对应的波束宽度的变化；

2）要准确反映天线增益，特别是不同的天线指向对应的天线增益的变化；

3）要准确反映方向图旁瓣，特别是不同的天线指向对应的方向图旁瓣的变化。

准确反映波束宽度、天线增益和方向图旁瓣，是对一般天线方向图进行仿真的共同要求，而准确反映不同的天线指向对应的波束宽度、天线增益和方向图旁瓣的变化，则是对相控阵天线方向图进行仿真的特殊要求。

从基本原理出发[10]，相控阵天线指向偏离阵面法线方向时，天线口径尺寸在该指向的垂直面上的投影面积发生变化，是波束宽度和天线增益发生变化的根本原因。在阵因子的表达式式（5）和方向性因子的表达式式（3）中，对这个原因进行了严格的、本质的反映。因此，通过计算式（5）和式（3）对相控阵天线进行仿真，对于表现波束宽度和天线增益的变化，是最直接、最自然、最准确的。仅直接利用式（5）和式（3）仿真相控阵天线的主要问题是方向图的旁瓣较高，而工程上实际使用的相控阵天线的方向图旁瓣会有大幅度的降低。解决这个矛盾的方法是在阵因子和方向性因子的基础上再增加一个旁瓣抑制因子。

2 相控阵天线方向图仿真的具体实现

综上所述，这里提出由阵因子、方向性因子和旁瓣抑制因子三者的乘积作为总体仿真模型，对相控阵天线方向图进行仿真的方法。即用下面的式（7）代替前面的式（1）：

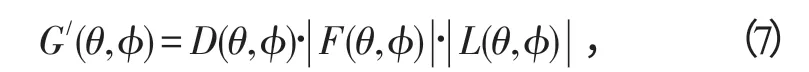
式中，L(θ,ϕ)为旁瓣抑制因子。

与阵因子、方向性因子一样，旁瓣抑制因子L(θ,ϕ)中也隐含了波束指向(θ0,ϕ0)的因素。

以下对这3个因子的仿真实现分别进行阐述。

2.1 关于阵因子的仿真实现

阵因子的仿真实现首先要进行静态参数计算，式（5）中的dx、dy、N和M是需要计算的静态参数。为避免在一定的角度范围内出现栅瓣，通常有

N和M分别决定于波束指向为阵面法线方向时，相控阵天线在x轴方向上的波束宽度θ0x和y轴方向上的波束宽度θ0y，有[10]：

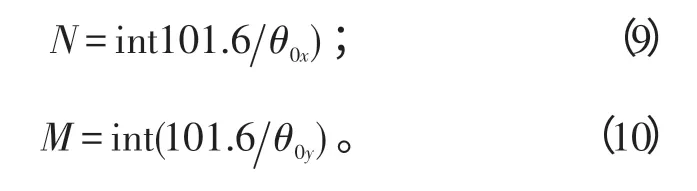
式（9）、（10）中的int（）是取整函数，θ0x、θ0y的单位是度。

将上述计算结果代入式（5），得到：

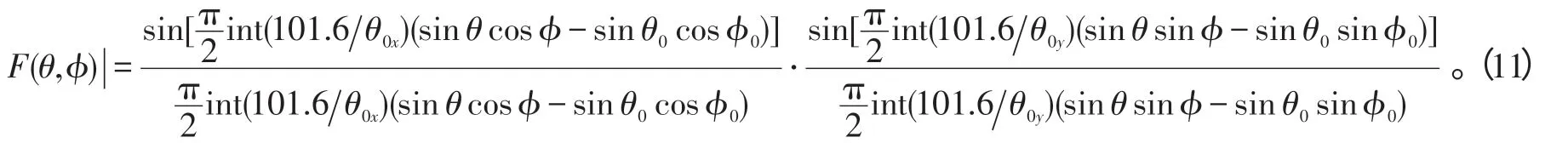
在进行仿真时，只要将当前天线的指向角（θ0、ϕ0）代入式（11），天线波束的宽度以及在任一空间方向（θ、ϕ）上呈现的归一化增益通过（11）的直接计算都准确地呈现了出来。

换句话说，阵因子仿真实现就是对式（11）的直接计算，不需要再考虑任何其他因素和转换关系。

作为比较，按照文献[11]的方法，为反映天线指向变化导致的波束宽度的变化，要进行4步计算：

第1步，要按照式（6）进行波束指向偏离阵面法线θ0角度时的波束宽度Bθ0的计算；

第2步，要进行Bθ0与以x为自变量的辛克函数的0.707点x0的转换，即

第3步，要进行半功率点之间的辛克函数计算；

第4 步，还要进行半功率点到第一零点的拟合函数计算（第5步的计算属于旁瓣抑制，不应在此进行比较）。

而按照这里给出的方法，仅需进行第3 步的辛克函数计算，不但减少了仿真计算量，而且波束宽度的精度（主要指天线指向变化时的波束宽度的精度）更高（因为这里没有一阶近似）。

2.2 关于方向性因子的仿真实现

方向性因子决定了天线增益以及天线指向变化导致的天线增益变化。其中，天线指向变化导致的天线增益变化主要体现在上，而加权效率以及失配和综合欧姆损耗总和随天线指向的变化并不明显。因此，在仿真中，方向性因子D(θ0,ϕ0)简化为

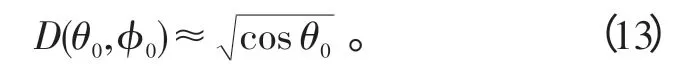
这里，方向性因子的应用与文献[11]相同，仿真计算量也相同。

2.3 关于旁瓣抑制因子的仿真实现

无论在工程实现上还是在仿真上，对于旁瓣抑制，通常关心的是第一旁瓣电平以及总体旁瓣水平。对于第一旁瓣电平，可以直接指定；而总体旁瓣水平由第一旁瓣电平和旁瓣函数共同决定。

在这里，给出作为旁瓣抑制因子的典型函数（x轴方向上的），该函数中，显式地以θ0作为参数：

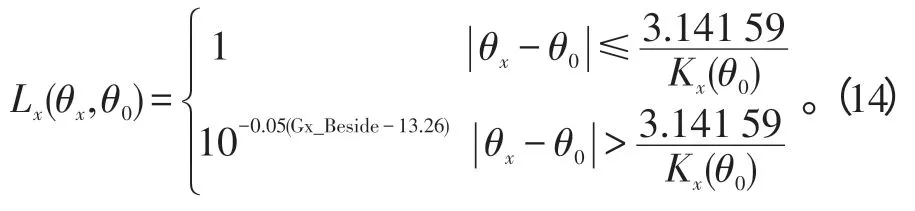
式（14）中：θx为天线指向在xoz平面上投影与z轴的夹角；Kx(θ0)为天线方向图在x轴方向上的第一个零点的位置；Gx_Beside 为第一旁瓣电平。

对于Kx(θ0)，有

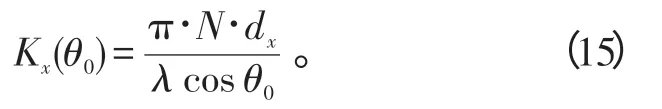
针对就仿真计算量而言，这里的旁瓣抑制因子与文献[11]没有实质上的差别。

3 仿真验证

下面针对美国海军宙斯盾系统中的AN/SPY-1D雷达，按上述方法和模型，给出在xoz平面上其归一化天线方向图的仿真结果。

波束指向阵面法线时，AN/SPY-1D雷达天线的波束宽度为1.8°，第一旁瓣电平为-29 dB[14]。波束指向阵面法线及波束指向在xoz平面上偏离阵面法线60°时，仿真得到的AN/SPY-1D雷达天线在xoz平面上的归一化天线方向图分别如图2、3所示[15]。

图2中，天线波束以0°为中心，天线波束的角度范围为-6°～6°。由图可见，在波束中心，方向图的增益为0 dB；天线增益-3 dB 处对应的2 个角度分别为-0.9°和0.9°，表明天线的波束宽度为1.8°；第一旁瓣电平为-29 dB。与仿真对象的相关参数完全一致。

图3 中，天线波束以60°为中心，天线波束的角度范围为54°～66°（即以60°为中心的-6°～6°）。由图可见，在波束中心，方向图的增益为-3 dB；天线增益-6 dB（即相对于波束中心增益下降3dB）处对应的2个角度分别为58.2°和61.8°，表明天线的波束宽度为3.6°、第一旁瓣电平为-32 dB。方向图增益的下降、天线波束的展宽以及第一旁瓣电平的变化与理论分析结果吻合得很好。

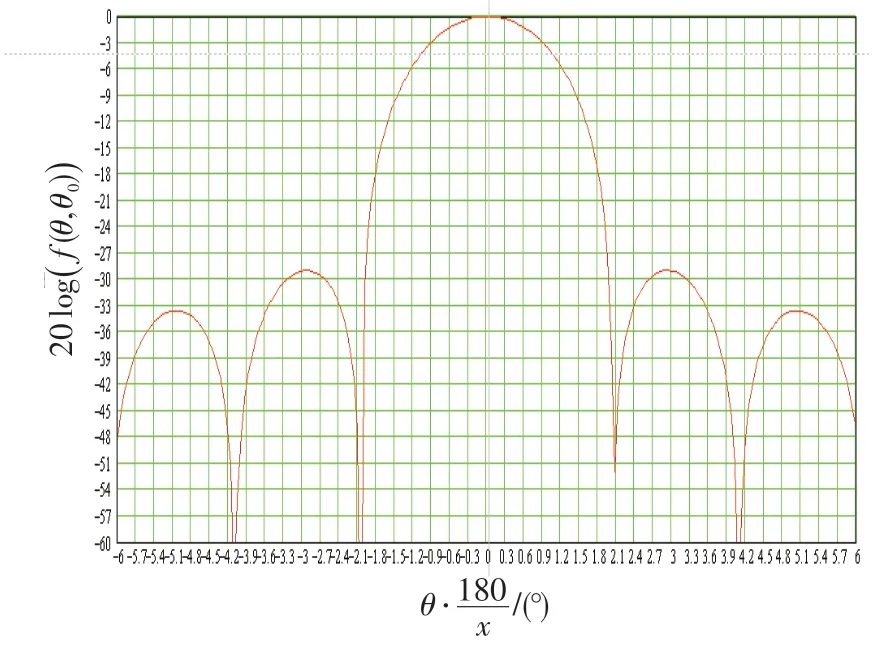
图2 波束指向阵面法线时AN/SPY-1D雷达天线在xoz 平面上的归一化天线方向图Fig.2 Normalized directional diagram of the antenna of AN/SPY-1D on xoz plane as beam pointing the normal of the antenna array

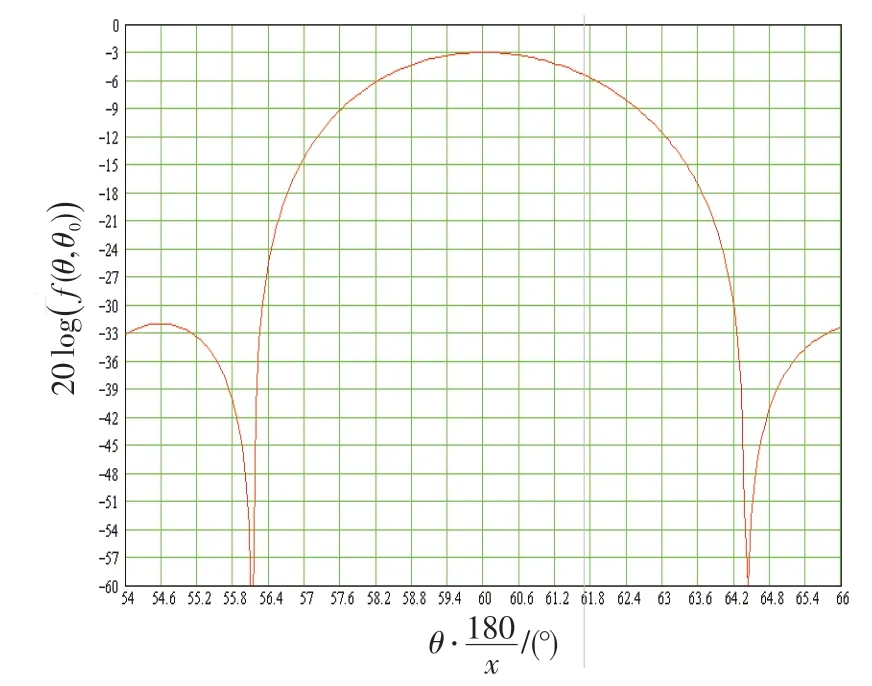
图3 波束偏离阵面法线60°时AN/SPY-1D雷达天线在xoz 平面上的归一化天线方向图Fig.3 Normalized directional diagram of the antenna of AN/SPY-1D on xoz plane as beam deviating 60°from the normal of the antenna array

4 结束语

相控阵天线无论在理论、技术和工程上都已成熟，但相控阵天线的仿真一直是人们所关注的一个重要问题。本文从相控阵天线的基本原理出发，针对相控阵天线仿真的基本和主要问题，提出了一种利用阵因子、方向性因子和旁瓣抑制因子分别解决仿真波束形状、天线增益、方向图旁瓣及其变化等3 大问题，然后再进行综合的建模和仿真的方法。这种方法具有自然、原理清晰、条理清楚、灵活可控的特点，所产生的模型不仅可以达到理论方面的高精度、还可以与实际天线有很好的吻合，在仿真计算步骤和计算量上也有较好的优化和减少。

该方法以及所产生的模型已经在一个信号级的相控阵雷达作战应用仿真项目中得到应用，取得了好的效果。

[1] DALE R BILLETTER. Multifunction array radar[M].Norwood：Artech House，1989：71-77.

[2] 陈忠先.相控阵雷达的发展前景[J].雷达科学与技术，1995（3）：1-6.

CHEN ZHONGXIAN. Thedevelopment and prospect of phased array radar[J]. Radar Science and Technology，1995（3）：1-6.（in Chinese）

[3] YU S J，LEE JUHONG. Efficient eigenspace-based array signal processing using multiple shift-invariant subarrays[J]. IEEE Transactions on Antenna Propagation，1999，47（1）：186-194.

[4] 袁海杰.相控阵天线数字波束形成浅述[J].火控雷达技术，2003，32（32）：31-37.

YUAN HAIJIE.Digital beam forming in phased array antenna[J]. Fire Control Radar Technology，2003，32（32）：31-37.（in Chinese）

[5] 郭金良，张钰，汪连栋，等.舰载相控阵雷达仿真系统研究与实现[J].系统仿真学报，2010，22（11）：2571-2574.

GUO JINLIANG，ZHANG YU，WANG LIANDONG，et al. Research and realization of shipborne phased array radar simulation system[J]. Journal of System Simulation，2010，22（11）：2571-2574.（in Chinese）

[6] 韩建兴，窦林涛.舰载相控阵雷达功能仿真建模与软件设计[J].船舶电子工程，2008（6）：130-133.

HAN JIANXING，DOU LINTAO. Modeling and software-design of function simulation of shipborne phased array radar[J]. Ship Electronic Engineering，2008（6）：130-133.（in Chinese）

[7] 张社欣，李文臣，郭新海.密度加权相控阵天线方向图仿真[J].舰船电子对抗，2006，29（4）：73-76.ZHANG SHEXIN，LI WENCHEN，GUO XINHAI.Direction pattern simulation of density weighted phased array antenna[J]. Shipboard Electronic Countermeasure，2006，29（4）：73-76.（in Chinese）

[8] 王国玉，汪连栋，王国良，等.雷达电子战系统数学仿真与评估[M].北京：国防工业出版社，2004：94-114.

WANG GUOYU，WANG LIANDONG，WANG GUOLIANG，et al. Mathematical simulation and evaluation of radar electronic warfare system[M].Beijing：National Defense Industry Press，2004：94-114.（in Chinese）

[9] 张光义.相控阵雷达原理[M].北京：国防工业出版社，2009：37-42.

ZHANG GUANGYI.Principles of phased array radar[M].Beijing：National Defense Industry Press，2009：37-42.（in Chinese）

[10]丁鹭飞，强伯涵，陈圆琴，等.雷达系统[M].北京：国防工业出版社，1980：191-194.

DING LUFEI，QIANG BOHAN，CHEN YUANQIN，et al. Radar system[M]. Beijing：National Defense Industry Press，1980：191-194.（in Chinese）

[11]陈志杰，李永祯，戴幻尧，等.相控阵天线方向图的建模与实时仿真方法[J].计算机仿真，2011，28（3）：31-35.

CHEN ZHIJIE，LI YONGZHEN，DAI HUANYAO，et al.Modeling and real-time simulating of phased-array antenna’s directional pattern[J]. Computer Simulation，2011，28（3）：31-35.（in Chinese）

[12]常硕，王德功，李圭源.相控阵雷达天线方向图仿真研究[J].中国雷达，2008（1）：35-37.

CHANG SHUO，WANG DEGONG，LI GUIYUAN.Study on simulation of phased array radar antenna[J].China Radar，2008（1）：35-37.（in Chinese）

[13]王国玉，张钧，马剑武.多功能相控阵雷达的相控阵天线仿真数学模型[J].雷达与对抗，1997（3）：12-15.

WANG GUOYU，ZHANG JUN，MA JIANWU. Mathematic simulating model of phased-array antenna in multifunction array radar[J]. Radar & Ecm，1997（3）：12-15.（in Chinese）

[14]何川.“宙斯盾”系统[J].电子对抗技术，2004，19（1）：47-48.

HE CHUAN. Aeyis system[J]. Electronic Warfare Technology，2004，19（1）：47-48.（in Chinese）

[15] 张起豪. Mathcad 4.0/5.0[M]. 北京：人民邮电出版社，1996：162-164.

ZHANG QIHAO. Mathcad 4.0/5.0[M]. Beijing：Post &Telecom Press，1996：162-164.（in Chinese）