轨道不平顺波长对桥上CRTS II型板式轨道振动特性的影响

房建，雷晓燕，练松良

（1.同济大学交通运输工程学院，上海201804；2.华东交通大学铁路环境噪声与振动工程中心，江西南昌330013）

随着我国综合国力的提升以及科技水平的进步，我国高速客运专线进入了高速建设期。高架结构作为高速客运专线的主要形式，引发的振动、噪声问题越来越明显，其根源之一在于轨道不平顺。试验表明，轨道不平顺的波长、幅值不同，对车辆—轨道动力响应所起的激扰作用也不同［1］。高速客运专线行车速度高，轨道不平顺引起的列车振动和轮轨相互作用力将随着列车速度的提高成倍增大。对高速客运专线而言，在严格实行轨道不平顺幅值管理与均值管理的基础上，还必须考虑轨道不平顺波长对车—轨—桥动力性能的影响，其中轨道不平顺幅值控制较容易，但波长控制相对更为复杂。高速铁路的波长管理成为高速铁路运营亟待解决的问题。

针对线路不平顺波长管理以及轨道不平顺的最不利波长范围，很多学者做了研究工作。徐庆元［2］、左玉云［3］采用车辆-轨道竖向耦合振动模型，分析了车辆随机振动与轨道不平顺之间的关系。王开云［4］、陈果［5］主要分析了车辆横向振动响应与轨道不平顺之间的关系。房建、雷晓燕、练松良等［6］采用现场实测轨道不平顺数据，分析了车体振动加速度所对应的最不利波长。上述研究成果多集中在线路上的列车运行时最不利波长分析，而对高速线路高架轨道振动特性研究较少。基于上述分析，本论文建立了列车-轨道-桥梁耦合振动有限元模型，选用德国低干扰谱作为激励模型，分析高速线路不平顺激励下高架轨道结构的振动特性，着重研究轨道不平顺波长对轮轨力与轨道结构振动响应的影响规律。

1 车辆-轨道-桥梁耦合振动分析模型

要想详细分析轨道不平顺对高速列车高架轨道结构振动特性的影响，首先必须建立一个比较正确、完善的车辆-轨道-桥梁相互作用模型，当前主要采用振型叠加法或有限元法对该问题进行求解。振型叠加法只适用于线性问题，而且对复杂桥梁结构而言，由于多阶振型参与贡献，其计算自由度会大量增加，无法体现其优点。有限元法不仅对列车驶经桥梁进行全过程的分析，还可用于非线性问题，因此在分析车—桥耦合问题时被普遍采用，成为当前研究车辆-轨道-桥梁耦合振动的主流方法［7-9］。

本文利用文献［10-11］建立的车辆-轨道-桥梁耦合振动的有限元模型研究轨道不平顺波长的影响规律。在该模型中，将列车、多跨连续梁桥上CRTS II型板式轨道以及桥梁视为一个整体系统。一节车辆可被离散为一个车辆单元，车辆单元每个车轮下附有一系钢轨，该钢轨用于车辆与轨道之间的耦合，不计其质量和刚度。轨道单元是根据高速客运专线桥上CRTSⅡ型板式轨道结构轨道板、底座板跨梁缝连续铺设的特点，考虑钢轨、轨道板，混凝土支承层和桥面板以及相互作用关系的四层梁模型。将高速客运专线桥上CRTS II型板式轨道视为一个整体系统，利用轮轨之间相互关系进行耦合，由此建立列车-轨道-桥梁系统耦合振动的有限元方程，借助Matlab软件编制相应程序可计算分析列车-轨道-桥梁系统的振动响应。

2 轨道不平顺激励模型

由于我国还缺乏高速铁路轨道谱，本论文采用适用于车速250 km·h-1以上的德国高速铁路低干扰谱来模拟轨道不平顺，其表达式可参见文献［12］。为了研究不同波长不平顺对车-桥耦合系统动力性能的影响规律，设定如表1所示的5组不同波长范围的轨道不平顺样本，且设定车速为250 km·h-1。

表1 不同波长成份的轨道不平顺参数Tab.1 Track irregularity characteristicsatdifferentwavelength range

3 轨道不平顺波长对桥上CRTS II型轨道振动特性影响

对轨道不平顺引起的车辆-轨道-桥梁耦合系统振动响应进行分析时，将文献［5］中车辆、桥上CRTSII型板式轨道结构参数代入有限元模型，计算车辆-桥上CRTS II型板轨道桥梁动力响应，并对其进行时、频域分析，研究随机不平顺波长对桥上CRTSII型板轨道结构动力响应的影响。

3.1 轮轨力

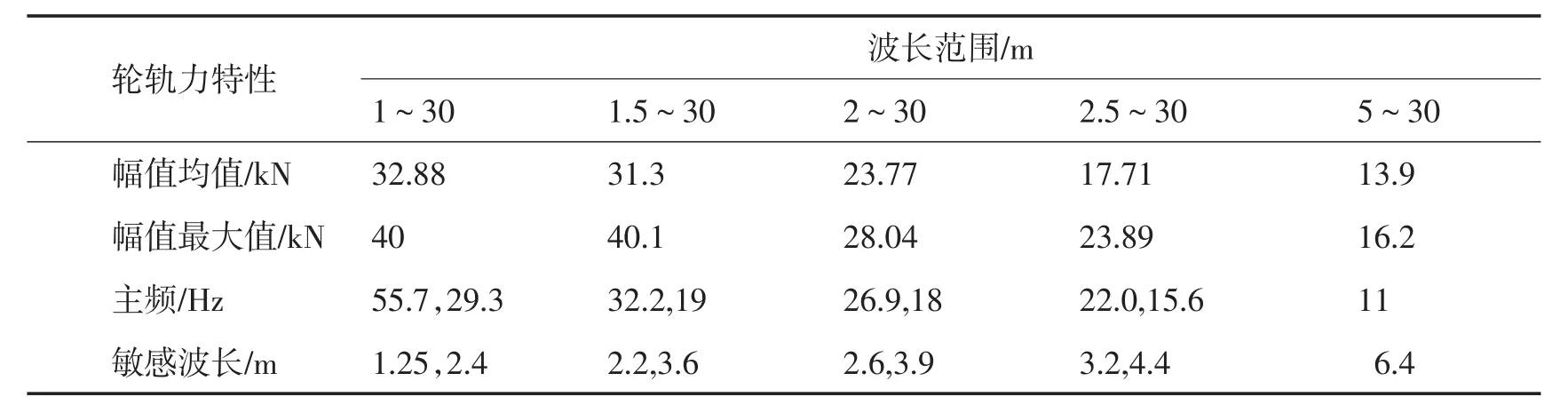
表2 不同波长范围不平顺激励下轮轨力特性Tab.2 Wheel-rail interaction force characteristics of differentwavelength irregularities

由图1、图2和表2可以得到：

1）在轨道不平顺激励幅值近似相等的条件下，轮轨动态作用力幅值的最大值与平均值随着轨道不平

表2为5种不同波长范围轨道不平顺激励下轮轨力幅值及主频特性，图1为波长范围1～30m的轨道不平顺激励下轮-轨相互动作用力。图2给出了轮轨力的频域响应曲线。顺激励中短波长的增大而显著减小，说明轨道不平顺中1m左右的短波长对轮轨力会产生显著影响。波长1.0m左右的不平顺对轮轨力的影响主要与轨道结构刚度、车辆一系悬挂刚度阻尼及轮对质量有关，其表现形式为瞬间高频脉冲峰值，尽管持续时间很短，但轮轨接触力会较静轮重增加数倍，从而导致轮轨踏面接触应力急剧增加。

2）随着短波长增大，轮轨力主频逐渐减小，对轮轨力产生主要影响的敏感波长随之增大。

3）轮轨力幅值能量主要集中在0.5～3Hz和12～35Hz范围内。在1～3Hz，25～40Hz频率范围内，五种不同轨道不平顺引起的轮轨力幅值能量按照不平顺激励中短波长的增大依次显著减小。

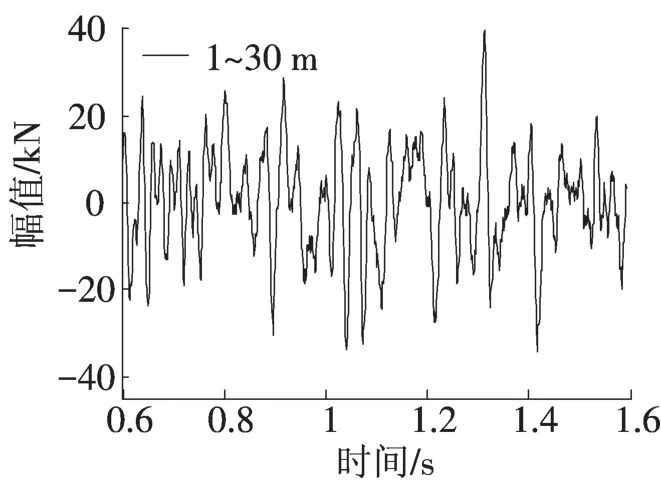
图1 1～30m波长范围不平顺激励下轮轨力Fig.1 Wheel-rail interaction forces produced by 1～30m wavelength range irregularities

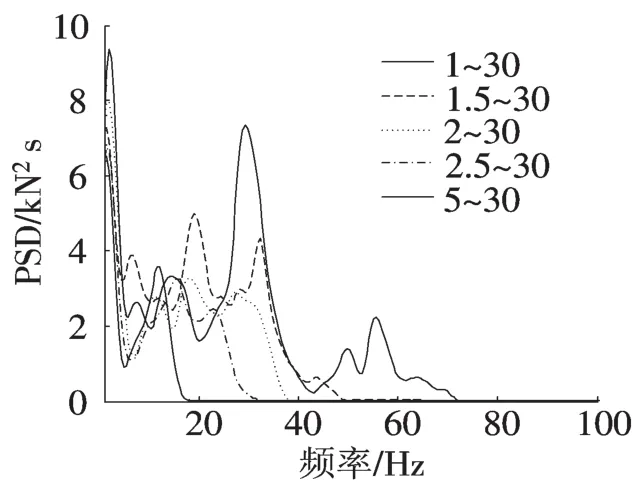
图2 不同波长范围不平顺激励下的轮轨力Fig.2 Wheel-rail interaction forces produced by different wavelength range irregularities

3.2 钢轨振动加速度

在5种不同波长范围的不平顺激励下，钢轨振动加速度幅值与主频如表3。限于篇幅，图3仅给轨道不平顺状态下钢轨振动加速度级。

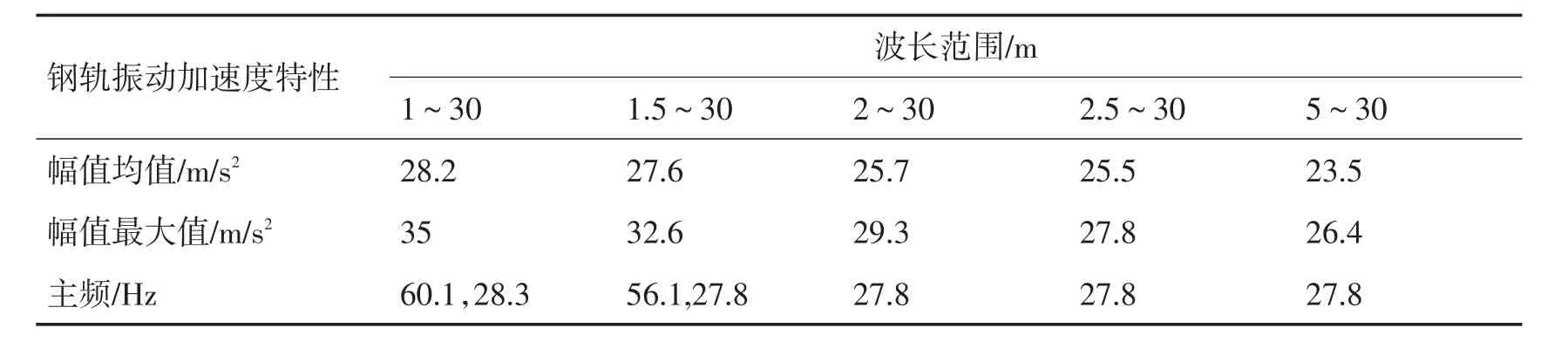
表3 不同波长范围的不平顺激励下钢轨振动加速度特性Tab.3 Rail vibration characteristicsof differentwavelength irregularities

由图3表3中数据可以得到：

1）钢轨振动加速度幅值最大值、平均值均随不平顺激励中短波长的增大明显减小，说明轨道不平顺中1m左右的短波长对钢轨振动加速度会产生较大影响。这是由于1m左右的短波长成分会造成轮轨间显著的冲击作用，因此引起的钢轨加速度明显大于其他几种工况。

2）在五种不同波长范围的不平顺激励下，钢轨振动主要集中在20～40 Hz频率范围内。图3表明，在40～125Hz频率范围内，1～30m波长范围不平顺引起的钢轨振动加速度水平最大，按不平顺激励中短波长的增大而依次减小，钢轨最大振动加速度级分别为126，119.4，115，112和111 dB。

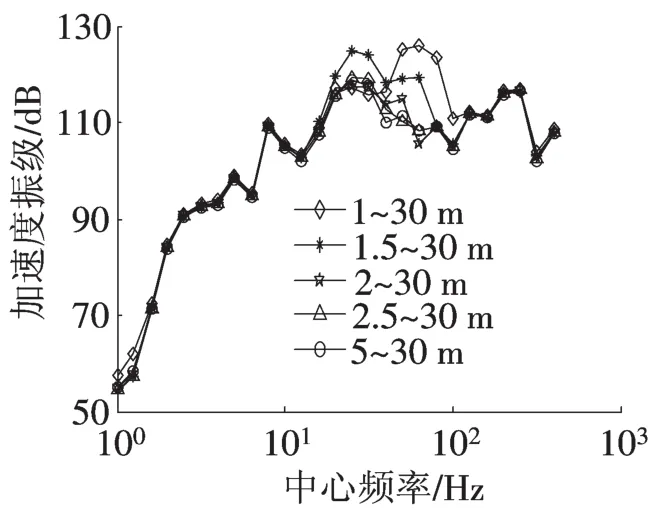
图3 不同波长范围的不平顺激励下钢轨振动加速度级Fig.3 Rail vibration level produced by differentwavelength range irregularities

3.3 轨道板振动加速度

在5种不同波长范围轨道不平顺激励下，轨道板振动加速度幅值与主频如表4；图4为轨道板振动加速度级曲线。

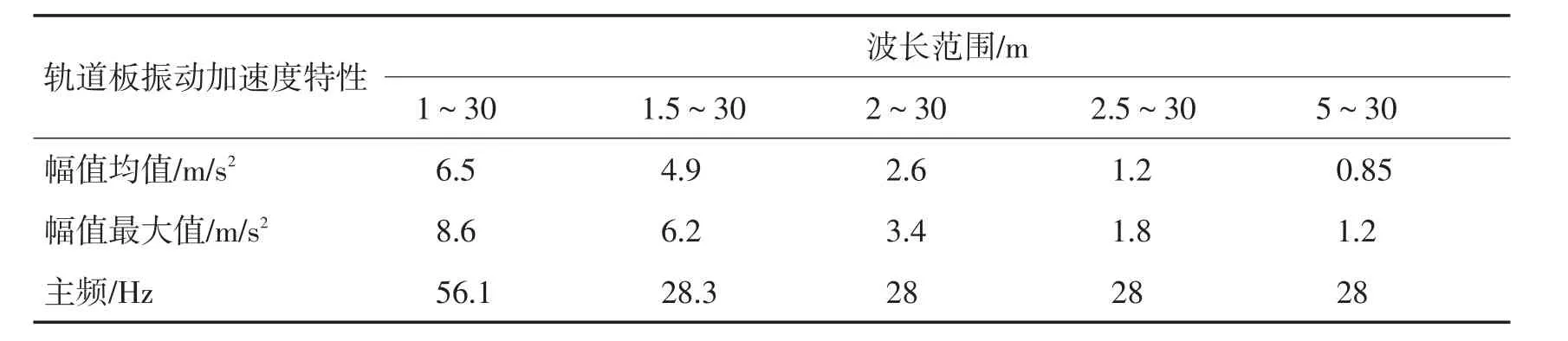
表4 不同波长范围的不平顺激励下轨道板振动加速度特性Tab.4 Track slab vibration characteristics of differentwavelength irregularities

由图4和表4可以得到：

1）轨道板振动加速度幅值最大值、平均值随着不平顺激励中短波长的增大而显著减小，说明轨道不平顺中1m左右的短波长对轨道板振动加速度也会产生较大的影响。

2）当最短波长从1m变化到1.5m时，轨道板振动加速度主频逐渐减小；当不平顺的波长范围分别为2～30m，2.5～30m和3.0～30m时，轨道板加速度振动主频不再变化，表现为不再受轨道不平顺短波长成分控制，主要与行车速度、轨道结构以及轨道板自身振动特性等多种因素有关。

3）在5种不同波长范围的不平顺激励下，轨道板振动主要集中在20～70 Hz频率范围。在31～70Hz的频率范围内，轨道板振动级随着不平顺激励中短波长的增大而减小，其最大振级分别为121.3，115.6，113.4，102和98 dB。

3.4 桥梁振动加速度

表5给出5种不同波长范围的轨道不平顺激励下，桥梁振动加速度幅值与主频；图5给出桥梁振动加速度级曲线。

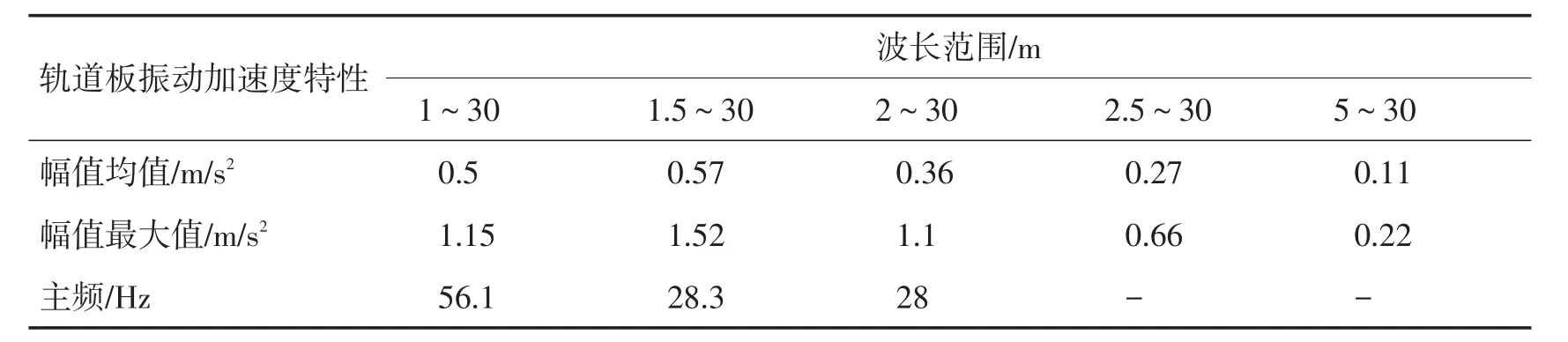
表5 不同波长范围的不平顺激励下桥梁振动加速度特性Tab.5 Bridge vibration characteristicsof differentwavelength irregularities

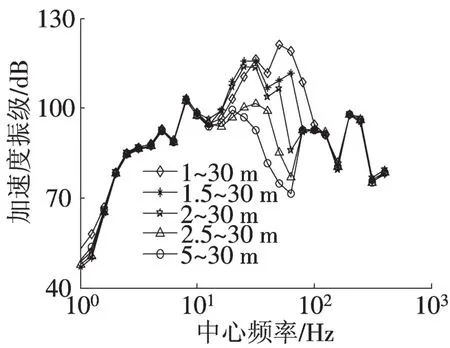
图4 不同波长范围的不平顺激励下轨道板振动加速度级Fig.4 Track slab vibration level produced by different wavelength range irregularities

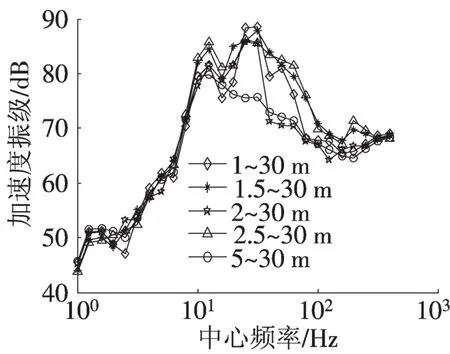
图5 不同波长范围不平顺激励下桥梁振动加速度级Fig.5 Bridge vibration level produced by different wavelength range irregularities

由图5和表5可以得到：

桥梁振动加速度幅值最大值、平均值基本随着不平顺激励中短波长的增大而减小。在5种不同波长范围不平顺激励下，桥梁振动主要集中在20～70Hz频率范围。图5表明，桥梁振动加速度级最大值为90 dB，桥梁振动水平处于较低水平。在10Hz以下频率范围，五种不同轨道不平顺引起的桥梁振动水平分布曲线数值相近。在25～30Hz频率范围内，桥梁振动级随着不平顺激励中短波长的增大而减小，桥梁最大振动加速度级分别为90，88，86，86和77 dB。

4 结论

1）轮轨力以及轮轨力能量均随着轨道不平顺短波长的减小而明显增大，说明轨道不平顺中1m左右的短波长对轮轨力会产生较大的影响。轨道不平顺对轮轨力的影响不仅体现在幅值上，轨道不平顺的波长分布特性也是影响轮轨相互作用的主要因素之一。

2）钢轨的竖向振动加速度幅值随着不平顺样本中短波长的减小而显著增大。在五种不同波长范围不平顺激励下，钢轨振动主要集中在20～125Hz频率范围。在40～125Hz频率范围内，1～30m波长范围不平顺引起的钢轨振动加速度水平最大，按轨道不平顺短波长的增大依次减小。

3）轨道板振动加速度的幅值随着不平顺样本中最短波长的减小而显著增大。在五种不同波长范围不平顺激励下，轨道板振动主要集中在20～70Hz频率范围内。在31～100Hz频率范围内，1～30m波长范围不平顺引起的轨道板振动加速度水平最大，按照轨道不平顺短波长的减小依次减小。

4）在5种不同波长范围不平顺激励下，桥梁的振动主要集中在20～70Hz频率范围。在10Hz以下频率范围，5种不同轨道不平顺引起的桥梁振动水平分布曲线数值相近。在25～30Hz频率范围内，桥梁振动级随着不平顺激励中短波长的增大而减小。

［1］ 韦红亮，练松良，周宇.轨面不平顺对高架支承块轨道结构振动特性影响研究［J］.中国铁道科学，2011，32（6）：22-27.

［2］ 徐庆元，曹扬风，周小林.短波随机不平顺对列车—板式无砟轨道—路基系统振动特性的影响［J］.中南大学学报，2011，42（4）：1105-1110.

［3］ 左玉云.铁路轨道不平顺对车轨系统竖向振动响应的影响分析［D］.中南大学，2009.

［4］ 王开云，翟婉明，刘建新，等.线路不平顺波长对提速列车横向舒适性影响［J］.交通运输工程学报，2007，7（1）：1-5.

［5］ 陈果，翟婉明，左洪福.轨道随机不平顺对车辆-轨道系统横向振动影响［J］.南京航空航天大学学报，2001，6，33（3）：227-232.

［6］ 房建，雷晓燕，练松良，等.提速线路轨道不平顺不利波长的研究［J］.铁道工程学报，2010，146（4）：27-31.

［7］ YANGY B，Y S，WU Y S.Dynamic stability of trainsmoving over bridges shaken by earthquakes［J］.Journal of Sound and Vibration，2002，258(1):65-94.

［8］ WU Y S，YANG Y B，YAU JD.Three-dimensionalanalysis of train-rail-bridge interaction problems［J］.Vehicle System Dynamies，2001，36（l）：1-35.

［9］ JU SH.Resonance of characteristics of high-speed trains passing simply supported bridges［J］.Journal of Sound and Vibration.2003，267（6）：1127-1141.

［10］ 房建.轨道不平顺对高速客运专线高架轨道结构振动特性的影响［D］.上海：同济大学，2013.

［11］ 陈松，雷晓燕，房建.客运专线车线桥垂向耦合系统振动的特性［J］.华东交通大学学报，2011，28（5）：41-45.

［12］ 雷晓燕.轨道力学与工程新方法［M］.北京：中国铁道出版社，2002：49-50.