霍山山前断裂带冲沟纵剖面数学拟合函数的构造响应特征*
毕丽思,何宏林,徐岳仁,魏占玉,石 峰,孙浩越
(1. 广东省地震局地震监测与减灾技术重点实验室,广东 广州 510070;2. 中国地震局地质研究所活动构造与火山重点实验室,北京 100029;3. 中国地震局地震预测研究所,北京 100036)
在自然界中,河流地貌广泛发育,其形成、发育、演化受构造活动的影响十分显著,是构造地貌研究中最常用和最受关注的地貌标志之一。在河流地貌中,河流纵剖面形态的调整与地壳运动紧密相关,对流域内断裂活动极为敏感,即使是地壳活动较为缓慢的情况下亦不例外[1-4]。因此,构造地貌学发展了多种描述河流纵剖面形态的参数,用来定量描述河流纵剖面的发育特征及其对构造运动的响应和调整[5]。随着高分辨率DEM(Digital Elevation Model,数字高程模型)数据的大量出现以及空间分析技术的迅速提高,人们研究河流发育特征与断裂活动相互关系的数据空间尺度越来越小(可达百米),精度越来越高。而且,基于DEM数据人们可以快速提取河流纵剖面并对河流纵剖面进行相关参数的快速定量计算。在描述河流纵剖面形态的众多参数中,河流纵剖面的数学拟合函数是最简单、最常用的参数之一,它从整体上直观地描述了河流纵剖面的凹曲形态。近年来,学者们通过河流纵剖面的数学拟合函数来分析河流发育对构造运动的响应特征,并取得了良好成果[6-8]。本文以霍山山前断裂带为研究区,基于高分辨率DEM数据,通过数学拟合函数分析横跨断裂带发育的冲沟的纵剖面形态特征,研究冲沟发育对霍山山前断裂带构造活动的响应特征。
1 研究区概况
霍山山前断裂带位于山西临汾盆地东缘北段的霍山西麓,是临汾盆地北部的盆地主控边界断裂,产状0-20°/W∠60-80°,全长大于60 km,在空间上可明显分为北、中、南三段,运动性质以正断为主兼有右旋走滑分量(图1)[9]。自上新世形成以来霍山山前断裂下盘表现出十分强烈的抬升作用,断裂带两侧的差异升降运动幅度达3 443 m[10],全新世以来断裂的平均垂直运动速率为0.7 mm/a[11]。古地震及历史地震的调查结果表明,全新世以来,该断裂有过多次强烈活动,最新一次强震事件为1303年洪洞8级地震,地表破裂带长达45 km,同震产生了地震陡坎、地堑、断错水系、眉脊面和构造楔等[12-13]。横跨断裂带的冲沟十分发育,为研究冲沟发育对霍山山前断裂带构造活动的响应提供了良好的先决条件。
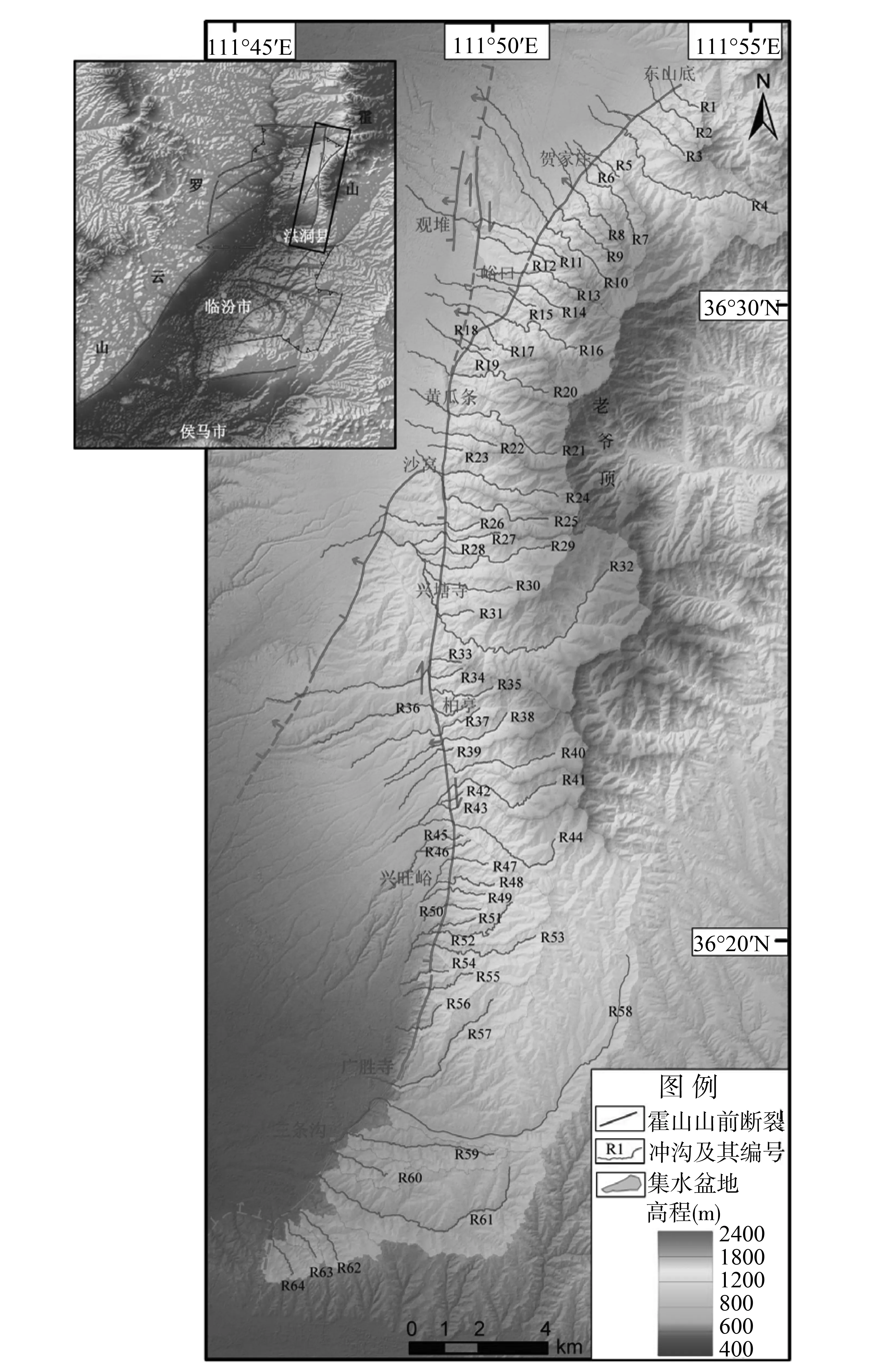
图1 霍山山前断裂带构造与地貌略图(底图为空间分辨率为2.5 m的IRS-P5 DEM数据)
2 河流纵剖面的数学拟合函数
河流的下凹形态是最容易从它的纵剖面上直接观察到的现象,而且下凹程度愈往上游愈大。一般来说,影响河流纵剖面整体形态的因素主要有三个,分别是河水流量、河床物质粒径以及河流输沙量[14-15],其他因素,如河道基岩、支流汇入、构造运动等,只与河流纵剖面的局部变化有关。从河流纵剖面的形态与变化可以了解河道沉积物、河道基岩形态、构造运动以及集水区流域演化等多种影响因素的特征以及河流的发展演化[15-16]。近年来利用简单数学函数进行河流纵剖面模拟的研究发展迅速,无论是利用数值模型模拟理想河流纵剖面还是野外实测的真实河流纵剖面的拟合分析,均取得不错的成果[6,15-16]。目前,用于河流纵剖面拟合的简单数学函数有以下四种(图2),其中Y为河流纵剖面的高程,X为河流纵剖面的长度,a与b皆为常数。
A.线性函数Y=a+bX
B.指数函数Y=aebX
C.对数函数Y=alogX+b
D.乘幂函数Y=aXb
基于上述四种简单数学函数,陈彦桀[7]指出,在构造运动不甚强烈、气候变化不甚剧烈等相对稳定的条件下,河流纵剖面的下凹程度与形态变化反映了河流演化的过程,其演化顺序为:线性剖面=>指数剖面=>对数剖面=>乘幂剖面(图2)。具体演化过程如下:地形面受到构造抬升作用后构造运动即停止,初始形成的河流其纵剖面的下凹程度较小或近乎直线,可用线性剖面来拟合,随着侵蚀作用在中上游进行并将侵蚀下来的物质搬运至下游堆积,使得河流纵剖面的下凹程度较大而逐渐演化成指数剖面,而后是对数剖面。如果河流流量增加或由于构造运动形成破碎带导致输沙量增加,破坏之前侵蚀作用与堆积作用的平衡,使得河流纵剖面的下凹程度快速增大而呈现出乘幂剖面。在这种模式中,河流纵剖面的形态发展明显与河流的发育时间紧密相关。而Rãdoane等[6]研究了罗马尼亚Carpathians地区的河流纵剖面形态后指出,河流纵剖面的形态变化与河流发育的时间关系不大,地壳的抬升速率才是最主要的影响因素。
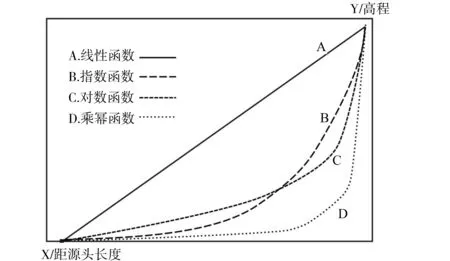
图2 四种拟合河流纵剖面的简单数学函数的剖面形态
3 高分辨率DEM数据的获取与数学函数拟合冲沟的选取
本文采用的数据是基于印度遥感制图卫星IRS-P5影像对的数字摄影测量获得的空间分辨率为2.5 m的DEM数据(图1)。所选用的IRS-P5卫星影像数据均为标准3级产品(OrthoKit产品),没有云、雪覆盖,地物的几何结构和纹理信息清晰。本文采用数字摄影测量专业软件,进行有地面控制点的高分辨率DEM提取,并用等高线套合分析法、检查点法和剖面线法对获得的DEM数据进行精度评价。结果表明,本文基于IRS-P5卫星影像对提取的DEM其精度达到了1∶1万DEM的标准[17]。
由于一条河流从上游到下游其河道剖面的演化性质并不尽相同,位于最上游的一级河河段,其上游的集水盆地面积较小,崩积作用所造成河床高程的增加效果比地壳抬升作用的影响还明显,而位于最下游的河段,其河道中河床高程的增加则受到冲积作用的强烈影响,因此在分析河流纵剖面形态受构造抬升作用的影响时,主要以分析河床高程受基岩抬升作用影响显著的基岩河道为主。由于霍山山前断裂位于山前,断裂的上升盘基本为基岩,断裂位置基本上是冲沟上游基岩河道与下游堆积河道的分界,因此,本文在分析横跨断裂带冲沟的纵剖面形态时,冲沟的出水口选择在霍山山前断裂位置处,出水口的上游流域为集水盆地,所分析的冲沟为集水盆地内长度最长的主干河道。本研究区内跨越断裂带的冲沟数量多,发育长度长短不一,本文选择断裂带上游长度不短于500 m的冲沟为研究对象,基于上述所获取的DEM数据由北往南一共提取了64条冲沟,编号依次为R1,R2,……,R64,相应位置如图1所示,每条冲沟的基本信息统计在表1。
4 冲沟纵剖面数学函数拟合结果
本文在利用简单数学函数进行实际冲沟纵剖面拟合分析时,用以判断哪一种数学函数拟合得最佳的依据主要有两个:一是参考该数学函数与实际冲沟纵剖面间统计回归的判别系数(R2)(表1);二是目视判断该数学函数的凹曲形态与实际冲沟纵剖面形态的吻合程度(图3)。在所分析的冲沟纵剖面中,拟合度(R2)最高的函数均集中在线性函数与指数函数中。除了少数几条冲沟外(R23、R31的线性函数拟合,R7、R53的指数函数拟合),其余冲沟的线性函数与指数函数的拟合度都在0.9以上,而所有冲沟的对数函数和乘幂函数的拟合度都较低,尤其是乘幂函数,其与实际冲沟纵剖面的拟合度几乎都低于0.6。因此,冲沟的最佳拟合函数在线性函数与指数函数中选择。
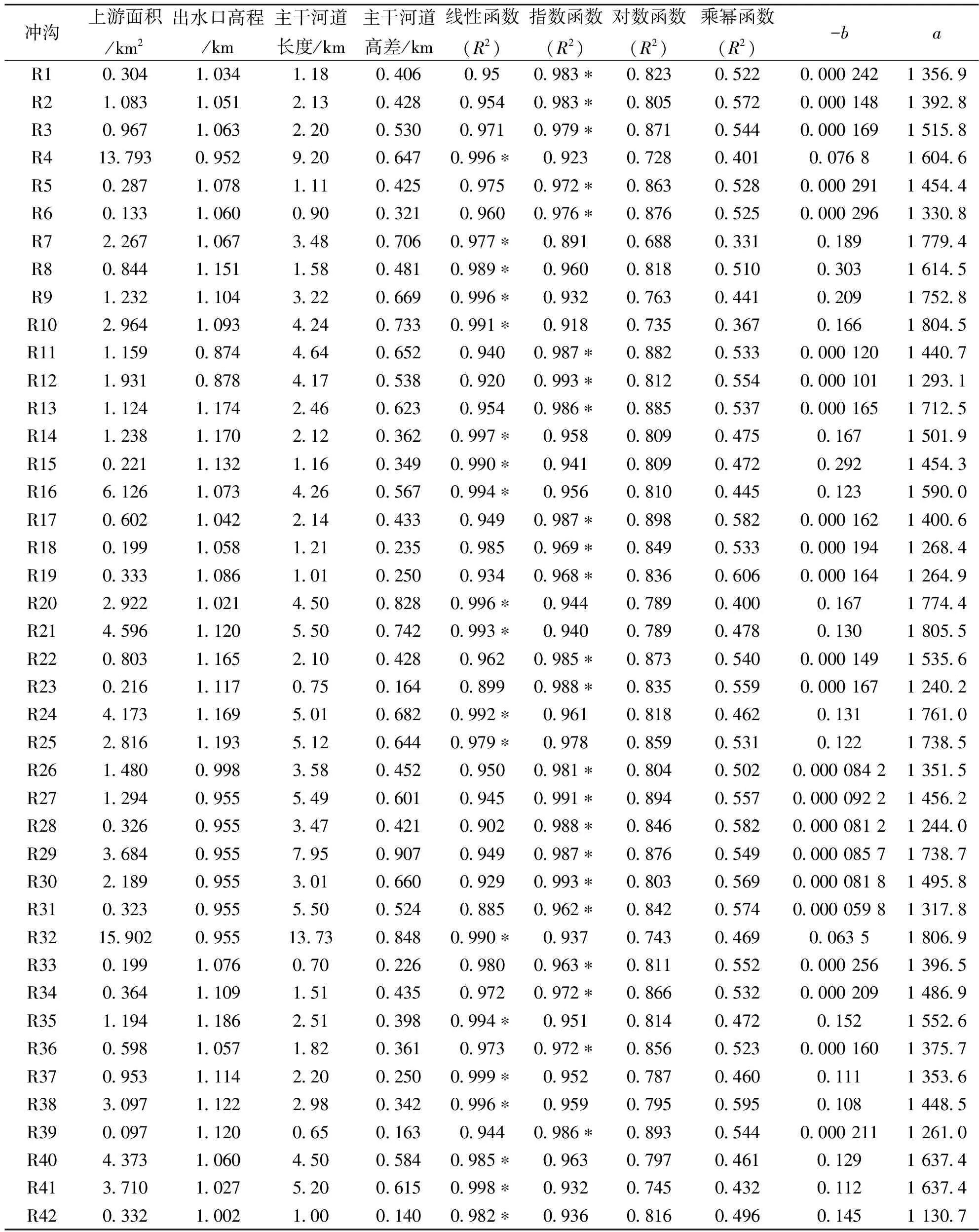
表1 64条冲沟的基本信息及四种数学函数拟合度统计表
续上表
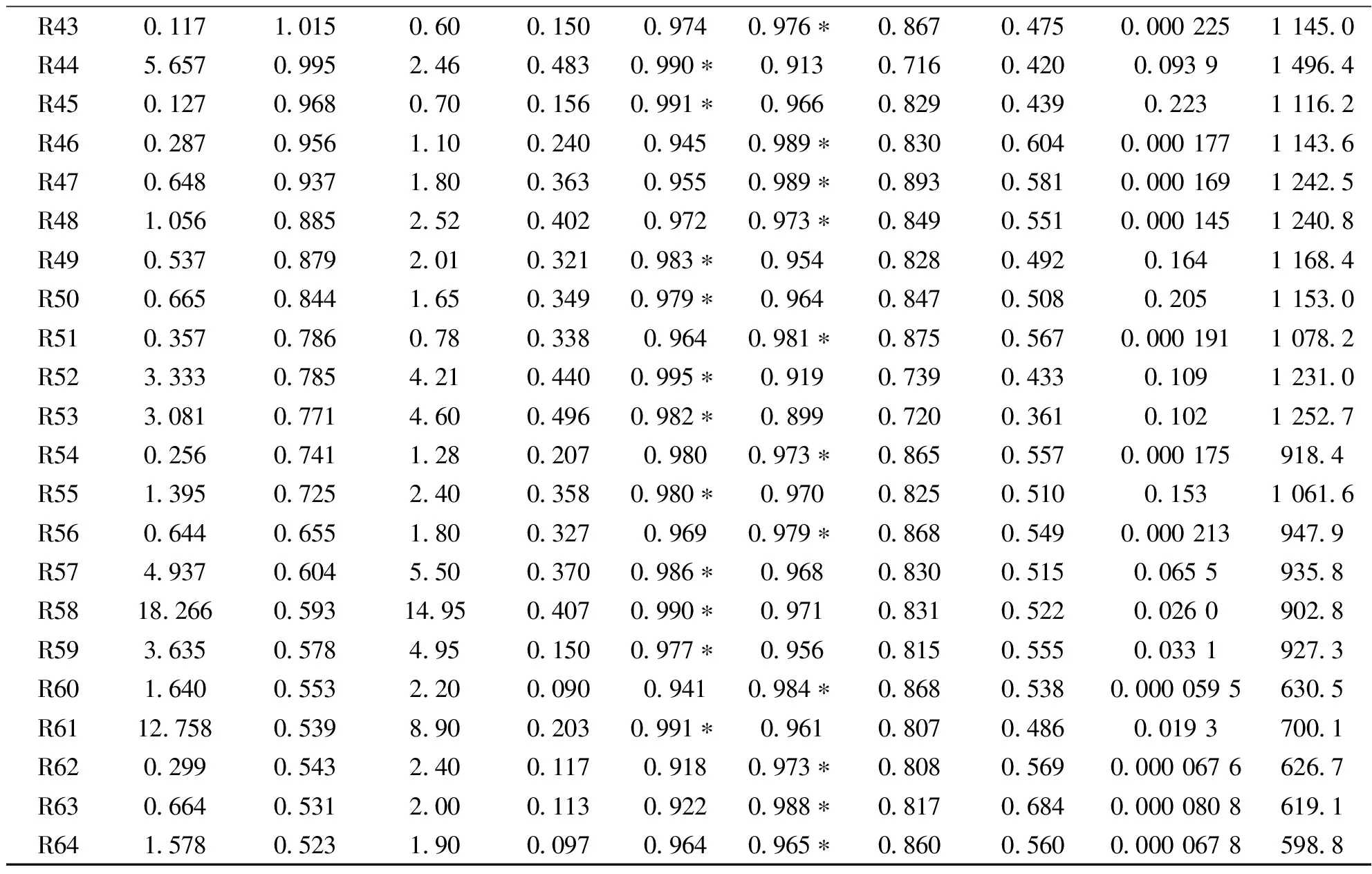
R430 1171 0150 600 1500 9740 976∗0 8670 4750 0002251145 0R445 6570 9952 460 4830 990∗0 9130 7160 4200 09391496 4R450 1270 9680 700 1560 991∗0 9660 8290 4390 2231116 2R460 2870 9561 100 2400 9450 989∗0 8300 6040 0001771143 6R470 6480 9371 800 3630 9550 989∗0 8930 5810 0001691242 5R481 0560 8852 520 4020 9720 973∗0 8490 5510 0001451240 8R490 5370 8792 010 3210 983∗0 9540 8280 4920 1641168 4R500 6650 8441 650 3490 979∗0 9640 8470 5080 2051153 0R510 3570 7860 780 3380 9640 981∗0 8750 5670 0001911078 2R523 3330 7854 210 4400 995∗0 9190 7390 4330 1091231 0R533 0810 7714 600 4960 982∗0 8990 7200 3610 1021252 7R540 2560 7411 280 2070 9800 973∗0 8650 5570 000175918 4R551 3950 7252 400 3580 980∗0 9700 8250 5100 1531061 6R560 6440 6551 800 3270 9690 979∗0 8680 5490 000213947 9R574 9370 6045 500 3700 986∗0 9680 8300 5150 0655935 8R5818 2660 59314 950 4070 990∗0 9710 8310 5220 0260902 8R593 6350 5784 950 1500 977∗0 9560 8150 5550 0331927 3R601 6400 5532 200 0900 9410 984∗0 8680 5380 0000595630 5R6112 7580 5398 900 2030 991∗0 9610 8070 4860 0193700 1R620 2990 5432 400 1170 9180 973∗0 8080 5690 0000676626 7R630 6640 5312 000 1130 9220 988∗0 8170 6840 0000808619 1R641 5780 5231 900 0970 9640 965∗0 8600 5600 0000678598 8
“*” 表示相应冲沟的最佳拟合数学函数类型,b、a是该最佳拟合函数的具体参数值。
在进行冲沟纵剖面拟合分析时发现,当R2值大于0.96,而且与其他函数之差在0.02以上时,目视该数学函数的凹曲形态与实际冲沟纵剖面的形态的吻合程度亦为最高,该函数为最佳拟合函数;当某两种数学函数的R2值均较高(>0.96)但两者差异很小(<0.02),通过目视判别后,R2值最高的数学函数的凹曲形态与实际冲沟纵剖面形态的吻合程度不一定最高,反而R2值次之的函数的凹曲形态与实际冲沟纵剖面形态的吻合程度更好,此时选择R2值次之但凹曲形态与实际冲沟纵剖面形态吻合程度最高的数学函数为最佳拟合函数,如R5、R33、R34、R36、R54。经过上述判别后,所分析的64条冲沟中有30条冲沟的纵剖面的最佳拟合函数为线性函数,34条为指数函数(表1、图3),总体表现为轻微的下凹形态。
5 讨 论
河流纵剖面的形态受到河水流量、河床物质粒径、河流输沙量、河道基岩性质、构造运动以及发育时间等因素的影响。由于河水流量、河床物质粒径、河流输沙量等因素受地区气候条件以及河道基岩性质的影响显著,因此本文总结出四个影响河流纵剖面形态的主要因素:流域发育时间、地区气候特征、河床基岩性质以及构造运动等。下面将从这四方面分析霍山山前断裂带冲沟纵剖面的发育形态特征。
1)就时间因素而言,河流发育时间愈长,其纵剖面下凹程度愈大,愈趋向于对数函数或乘幂函数的凹曲形态[7]。当河流处于发育的幼年期时,河流发育长度短小,河流纵剖面的下凹程度小,常用线性函数拟合。在本文以线性函数为最佳拟合函数的30条冲沟中,其长度由1~15 km不等。如果说由于发育时间短,冲沟长度短,因而导致其纵剖面趋于线性函数形态,那么像R4、R32、R58、R61等冲沟的长度接近10 km甚至超过10 km,其纵剖面应该偏离线性函数形态,而事实上,其纵剖面的最佳拟合函数仍是线性函数,而且拟合度均达到或超过0.99,比长度不足2 km的冲沟(R8、R15、R42、R50)的线性拟合度还高。此外,在22条长度小于2 km的冲沟中,只有少部分(5条)冲沟纵剖面的最佳拟合函数是线性函数,而大部分(17条)是指数函数。因此,时间因素并不是影响霍山山前断裂带冲沟纵剖面形态的主要原因。
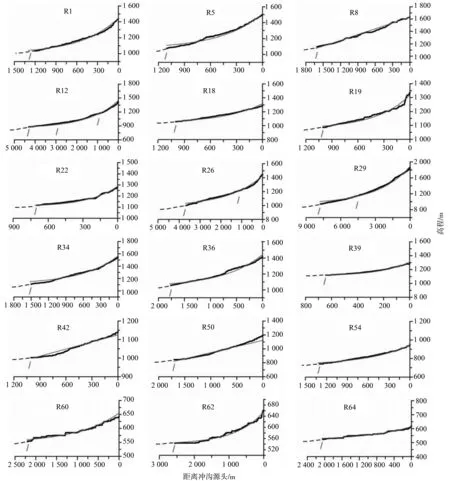
图3 霍山山前断裂带冲沟纵剖面及其最佳拟合数学函数(具代表性部分)(实线为实际冲沟纵剖面,虚线为最佳拟合数学函数,斜线(/)表示断裂位置。)
2)就气候因素而言,高山地区受地形降水的影响要比低山大,流经高山地区的河流由于雨量的增大以及地势的增高,其下切侵蚀作用增强,河流纵剖面下凹程度增大。但位于山麓带及霍山南部倾伏端低缓地区的冲沟(R1、R5、R6、R11、R12、R18、R19、R23、R39、R54、R60、R62、R63、R64)其纵剖面的下凹形态为指数函数,而流经高山区的冲沟(R4、R10、R20、R21、R24、R25、R32、R40、R41)其纵剖面的下凹形态为线性函数,呈现出高山多雨区的冲沟纵剖面的下凹程度比山麓少雨区的冲沟纵剖面的下凹程度小的异常情况。因此,气候条件也不是影响霍山山前断裂带冲沟纵剖面形态的主要原因。
3)在河道基岩性质方面,霍山山区北部为遭受混合岩化的中等区域变质岩系,中部为早古生代灰岩,南部为中生代砂岩以及新生代沉积,河道基岩的抗侵蚀强度由北往南大致呈减弱趋势,但本研究区冲沟纵剖面的下凹程度并没有表现出由北往南增大的趋势。因此,河道基岩性质也不是影响霍山山前断裂带冲沟纵剖面形态的主要原因。
4)在构造运动方面,霍山山前断裂带下盘自上新世形成以来表现出十分强烈的抬升作用,在上新世末至早更新世、中更新世中后期以及晚更新世至全新世,该断裂都有过强烈活动。自上新世以来断裂带两侧的差异升降运动幅度达3 443 m,断裂的平均垂直运动速率为0.69 mm/a[13]。第四纪以来霍山山前断裂带下盘一直处于隆升状态,全新世以来断裂的平均垂直运动速率为0.7 mm/a[11]。古地震及历史地震的调查结果还表明,全新世以来,霍山山前断裂带仍有过多次强烈活动[9,13]。在这种长期隆升的构造环境下,冲沟的发育显然受构造作用影响较大。一般说来,构造抬升速率愈大,河流受影响的强度愈大,河流的下切侵蚀作用愈强,河流的下凹程度愈大,但这以河流本身具有较强的侵蚀能力以及构造运动发生后有较长的平静期为条件(图4a)。本研究区处于半干旱区,年降水量偏小,河道基岩抗侵蚀能力强,河流的侵蚀作用较弱。根据Merritts等[18]的模型(图4b),河道受到抬升作用后在尚无侵蚀作用影响时,不同等级的河道坡度均不变。虽然本区域冲沟的侵蚀作用不为零,但区域内构造运动强烈而且频繁,全新世中晚期以来已发生过多次古地震事件,最新一次地震事件距今还不到800 a,其重复周期仅1 500-2 000 a[13]。每次构造运动发生后,冲沟还没来得及通过下切侵蚀作用来调整剖面形态,新一次的构造运动又发生。冲沟自形成后一直处于频繁而强烈的构造抬升运动中,其发育一直表现为幼年期的近直线的下凹程度很小的特征,而远远未发育到壮年期的对数函数形态或者老年期的乘幂函数形态。

图4 不同侵蚀强度的河流对相同构造抬升速率的响应(修改自Merritts and Vincent,1989)
另外,有34条冲沟的纵剖面形态为指数函数,这部分冲沟可分为两类,一类是河道发育十分短(R1、R2、R3、R13、R17、R18、R19、R22、R23、R33、R34、R36、R39、R43、R46、R47、R48、R51、R54、R56、R60、R62、R63、R64),主干河道长度均短于2.5 km。推测这类冲沟在构造抬升作用下,其侵蚀作用主要表现为下切侵蚀,溯源侵蚀作用则大为减弱,因此河道发育短,下凹程度有所增加。另一类冲沟的河道较长,约为4~8 km,其河道分别经过多条次级断裂,如观堆一带的R11、R12分别经过了三条次级断裂,兴塘寺一带的R26、R27、R28、R29、R30、R31则分别经过了两条次级断裂。由于次级断裂之间的活动性有所差异,受不同次级断裂影响的河段对构造运动的响应不尽相同,河道为了调整不同河段之间的差异,会通过下切侵蚀作用力求达到平衡,这样河道纵剖面的下凹程度会增大。
综合前文对时间、气候、基岩特性、构造运动等方面的分析,可以认为在霍山山前断裂带活动区域内,河流纵剖面的形态变化受构造抬升作用的影响非常显著。晚更新世以来,霍山山前断裂带地区河流的演化进程并没有随着时间的推移进化到均衡阶段,其主要原因就是受到霍山山前断裂带的构造活动影响,霍山山体持续隆升,河流地貌演化一直表现为幼年期的特征。
6 结 论
1)基于高分辨率DEM数据提取的横跨霍山山前断裂带的冲沟其纵剖面形态表现为表现为直线函数型以及略微下凹的指数函数型。
2)横跨霍山山前断裂带的冲沟的纵剖面形态特征反映了冲沟还处于幼年期,这是冲沟发育对断裂上新世以来强烈而频繁的正断层作用,尤其是全新世以来时间间隔较短的多次强烈活动的响应。
致谢:感谢中国地震局地质研究所张会平副研究员和中国地震台网中心赵洪壮副研究员在河流纵剖面定量参数研究上的指导和帮助,感谢中国地震局预测研究所王林博士在IRS-P5 DEM提取技术上的指导和帮助。
参考文献:
[1]SNOW R S, SLINGERLAND R L. Stream profile adjustment to crustal warping: nonlinearresults from a simple model [J]. Journal of Geology, 1990, 98: 699-708.
[2]LI Y, YANG J. Tectonic geomorphology in Hexi Corridor, northwest China [J]. Basin-Research, 1998, 10: 345-352.
[3]DELAILLAU B. Geomorphic response to growing fault-related folds: example from the foothills of central Taiwan [J]. Geodinamica Acta, 2001, 14: 265-287.
[4]HE H, OGUCHI T. Late Quaternary activity of the Zemuhe and Xiaojiang faults in Southwest China from geomorphological mapping [J]. Geomoophology, 2008, 96: 62-85.
[5]KELLER E A, PRINTER N. Active tectonics: earthquake, uplift, and landscape [M]. New Jersey: Prentice Hall Inc, 2002.
[7]陈彦桀. 台湾山脉的构造地形指标特性—以面积高度积分、地形碎形参数与河流坡降指标为依据[D]. 台湾:国立成功大学,2004.
[8]赵洪壮,李有利,杨景春,等. 河流纵剖面与基岩侵蚀模型特征分析[J]. 地理学报,2009, 64(5): 563-570.
[9]国家地震局《鄂尔多斯周缘活动断裂系》课题组. 鄂尔多斯周缘活动断裂系[M]. 北京:地震出版社,1988.
[10]徐锡伟,邓起东,韩竹君. 霍山山前断裂晚第四纪活动和古地震研究[M]∥马宗晋.山西临汾地震研究与系统减灾. 北京:地震出版社,1993: 136-148.
[11]刘光勋. 临汾盆地构造体系与地震[M]. 北京:科学出版社,1979.
[12]徐锡伟,邓起东. 山西霍山山前断裂晚第四纪活动特征和1303年洪洞8级地震[J]. 地震地质,1990, 12(3): 21-30.
[13]徐锡伟,邓起东. 1303年洪洞地震的地震构造[M]∥马宗晋.山西临汾地震研究与系统减灾. 北京:地震出版社,1993: 149-158.
[14]HACK J T. Stream-profile analysis and stream-gradient index [J]. U S Geological Survey Journal Research, 1973, 1: 421-429.
[15]SNOW R S, SLINGERLAND R L. Mathematical modeling of graded river profile [J]. Journal of Geology, 1987, 95: 15-33.
[16]OHMORI H, SAITO K. Morphological development of longitudinal profiles in Japan and Taiwan [J]. Bulletin of the Department of Geography, University of Tokyo, 1993, 25: 29-41.
[17]毕丽思,何宏林,徐岳仁,等. 基于高分辨率DEM的裂点序列提取和古地震序列的识别——以霍山山前断裂为实验区[J]. 地震地质,2011, 33(4): 963-977.
[18]MERRITTS D, VINCENT K R. Geomorphic response of coastal stream to low, intermediate, and high rates of uplift, Mendocino Triple Junction region, Northern California [J]. Geological Society of America Bulletin,1989, 110: 1373-1388.

