太湖流域降水不均匀性研究

邓鹏鑫，胡庆芳，王银堂，王磊之，崔婷婷

(南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏南京 210029)

在气候变化和城市化背景下，我国区域降水要素的变化及对旱涝情势的可能影响引起了广泛关注[1]。然而已有的研究多关注全年或年内特定时段降水总量的变化特征，对年内降水时程分布特征变化的研究相对较少[2-6]。而某一区域的水旱灾害，既与降水总量有关，也与降水年内分布密切相关。因此，在分析降水总量变化的同时，还应分析降水要素在年内分布的时间不均匀性及可能变化。

太湖流域是我国典型的平原河网地区，位于东亚季风气候区，降水时空分布不均，水旱灾害比较频繁。研究流域降水的时间不均匀性，可以更全面深入地理解太湖流域降水的时程分布特性，为流域水资源利用、水旱灾害分析提供科学依据。因此，本文同时采用信息熵分配紊乱指数(Apportionment entropy disorder index,ADI)[7-8]、基尼系数(Gini coefficient,GC)[9]和变差系数(Coefficient of variation,Cv)3种不均匀性指数，在旬、月时间尺度上分析全流域及分区域降水要素的不均匀性，并探讨不均匀指数变化对流域遭遇旱涝灾害情势的可能影响。

1 研究区域与数据

1.1 研究区域

图1 太湖流域DEM及水利分区Fig.1 DEM and drainage areas of the Taihu Lake basin

太湖流域位于东经119°11′～121°53′，北纬30°28′～32°15′之间，北抵长江，东临东海，南濒杭州湾，西以天目山、茅山等山区为界，流域总面积约36 895 km2。流域地形呈西高东低、四周高中间低之势，地貌特征以平原为主，山地丘陵仅分布在流域西部(图1)。太湖流域属典型亚热带季风气候，冬季干冷、夏季湿热，年均降水量为1 189 mm(1951—2011)。降水年内分布不均，汛期多年平均降水量为710 mm，约占全年的60%[10-11]。其中，5—7月为梅汛期，8— 9月为台风期。

根据流域地形及水系特点，将全流域分为湖西、浙西、太湖湖区、杭嘉湖、武澄锡虞、阳澄淀泖和浦东浦西7个分区。

1.2 研究数据

收集全流域和7个分区1951—2011 年逐日面降水量数据(太湖流域管理局水文局提供)。降水资料经过了质量控制，包括一致性、可靠性和代表性的分析处理。在逐日降水数据基础上，得到全流域及各分区年、汛期、月、旬降水数据。

2 研究方法

通常多采用变差系数(Cv)对降水的不均匀性进行分析，这一指标是描述样本相对均值的离散程度的一般性指标。近年来，一些学者相继探讨采用信息熵紊乱指数(ADI)[7-8]、基尼系数(GC)[9]等指标分析降水的不均匀性。其中，ADI能揭示序列变化的深层随机性，起源于热力学、统计力学领域；GC最早由意大利经济学家基尼(Gini)于1922年提出，用于社会财富分配平等性评价[12-15]。两项指标在降水不均匀性分析上已有成功案例[7-8]。

(1)

GC主要通过构建洛伦兹曲线进行不均匀性的定量评价[12-13]。流域降水时间分布不均匀性的洛伦兹曲线的构建方法可参考文献[9]。在对比多种GC计算方法[14]的基础上，本文采用张建华提出的简易公式[15]，该公式利用定积分的定义将洛伦兹曲线的积分分成n个等高梯形：

(2)

式中：Wt(t=1，2，3，…，n-1)为累积降水量的百分比，即将降水序列从小到大排列，依次计算累计降水量占总降水量的比值。

ADI是建立在信息熵概念的基础上，揭示要素深层随机性的指标。根据文献[7]，对于一组有限的随机序列x，信息熵H可表示为：

(3)

式中：xk(k=1，2，3，…，n)为样本序列；P(xk)为样本序列xk对应的经验频率。

在信息熵定义的基础上，进一步计算分配熵(Apportionment entropy，AE)：

(4)

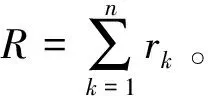
(5)

本文采用带预置白处理的Mann-Kendal趋势检验方法TFPW-MK(Trend-free pre-whitening Mann-Kendall)分析降水不均匀性指数的变化趋势。TFPW-MK与通常的MK(Mann-Kendal)方法相似，在给定某一置信水平时，当统计量的绝对值大于标准正态分布临界值时，则认为原序列趋势显著；否则，原序列趋势不显著。相比MK，TFPW-MK可消除序列正向自相关性，避免趋势显著性被放大，因而在序列数小于50，且变化趋势不是非常明显的情况下对趋势性的检测更为有效[17]。具体方法步骤可参考文献[16]。此外，引入Hurst系数来反映趋势性的持续性，当Hurst系数大于0.5，则认为未来趋势与当前趋势保持一致[7]。

3 结果分析与讨论

3.1 3种降水不均匀性指数的比较

本文基于全流域及7个分区1951—2011年逐旬、逐月面降水量时间序列，得到相应的ADI，GC和Cv，并计算各指数间的相关系数。表1中r1表示GC与Cv的相关系数，r2表示ADI与GC的相关系数，r3表示ADI与Cv的相关系数。

表1 3种不均匀性指数的相关系数Tab.1 Correlation coefficients of three heterogeneity indices

由表1可知，3种不均匀指数间的相关程度较高，仅武澄锡虞区和湖西区在全年旬尺度下，GC与Cv的相关系数值略低外，其他各分区指数间相关系数均大于0.93，其中，ADI与GC和Cv的相关系数大于0.95，最高可达0.98，整体反应出各指数间的差异很小。这与文献[8]的结果一致。但文献[8]认为，ADI基于概率密度函数的离散，避免了受到均值的限制，更能揭示要素的深层随机性。

本文以ADI为例，对降水的时程不均匀性作进一步阐述。其他指数的结果类似，本文不再赘述。

3.2 流域降水不均匀性指数与旱涝相关关系

旱涝灾害不仅与年或汛期降水总量有关，而且与降水的年内分布不均匀性密切相关。本文针对太湖流域年或汛期降水总量和不均匀指数与流域旱涝灾害的相关关系进行了初步分析。图2给出了1951—2011年全流域ADI值、标准化降水(即年或汛期降水量与多年最大值之比)的变化曲线。由图2(a)和(c)可知，在月尺度上，ADI值和年或汛期降水量在1954，1957，1962，1983，1991，1999和2010年均出现了较大值。由于降水量和ADI均较大，月降水分布不均，某些月份集中过量降水，较容易遭遇较大的洪涝灾害。如1954年、1991年和1999年均发生典型的梅雨型洪水。同时，ADI在1967，1971，1978，1994，2003和2011年出现较大值，而年或汛期降水量低于多年平均值。在降水总量较小，而ADI值较大的情况下，月降水量偏少，且分布不匀，较易产生干旱灾害。如1967和1978年为流域特枯干旱年。此外，若遭遇旱涝急转年时，年降水量偏低且过量集中于汛期，易造成月降水在汛期的分配较年分配均匀，呈现出在年或汛期分配下ADI值均较大的情况下，汛期降水量大于多年均值而相应年降水量却低于多年平均值。如太湖流域在2011年发生了60年来最严重的干旱以及典型的旱涝急转，其相应ADI值和汛期降水量高于多年平均值，而年降水量较多年平均值低。

(a) 全年月 (b) 全年旬

(c) 汛期月 (d) 汛期旬图2 1951—2011年全流域信息熵分配紊乱指数和标准化降水的变化曲线Fig.2 Variation in curves of standardized rainfall and ADI in the whole basin from 1951 to 2011

旬尺度下，流域降水不均匀性指数与旱涝的指示关系除与月尺度具有一致性外，还易反映出短历时强降水带来的灾害影响。由图2(b)和(d)可知，相比月尺度，旬尺度的降水分配差异更加显著。汛期旬尺度下，1963，1970，1991和2001年的ADI较汛期月尺度大，表明汛期旬降水分布较集中，遭遇短历时强降水，特别是台风型降水洪涝灾害的可能性较大，如1963和1970年为台风型洪涝年。

可见，结合降水总量，可初步反映出不均匀指数与旱涝具有一定的相关关系；但其与旱涝灾害对应的精确性还需作更深一步的探讨。

3.3 降水不均匀性指数的变化特征

表2给出了不同时间尺度下ADI的均值和极值。在旬时间尺度上，太湖流域全年和汛期的ADI最大值分别为1.12和1.38，最小值仅0.38和0.17，极值比为2.95和8.12；而月尺度下，全年和汛期的ADI极值比高达5.93和24.0。在各分区中，北部的武澄锡虞区和湖西区的特征值较大，全年旬尺度下的均值达到0.84和0.80，极大值为1.32和1.65，而南部浙西区和杭嘉湖区较小，相同尺度下均值仅0.67和0.71，极大值为1.31和1.32。这反映出太湖流域旬、月降水量在年内和汛期分配的不均匀性在不同年份的差异较大，且降水具有一定的空间分布差异，北部武澄锡虞区和湖西区降水的年内分布的不均匀性较其他各分区大。

采用TFPW-MK和MK两种非参数检验方法，结合Hurst 系数[8]，进一步检验了不均匀性指数的变化趋势性以及趋势的持续性。由表3可知，TFPW-MK和MK统计结果比较一致。两种方法都说明在汛期月尺度下，除湖西区和浦东浦西区外，其他各分区ADI指数均具有显著上升趋势，其中浙西区、太湖湖区、武澄锡虞区的TFPW-MK值甚至超过95%的置信度，Hurst系数分别为0.71，0.64和0.65，均大于0.5，上升趋势的持续性较强。

本文进一步对汛期各月降水量的变化趋势进行了检测，结果发现太湖流域5和9月降水呈现显著下降趋势，汛期降水愈趋集中于6—8月。这是汛期降水不均匀性指数增强的主要原因。而这也说明汛期流域降水分布趋于更集中的态势，较容易导致汛期洪涝灾害的发生。

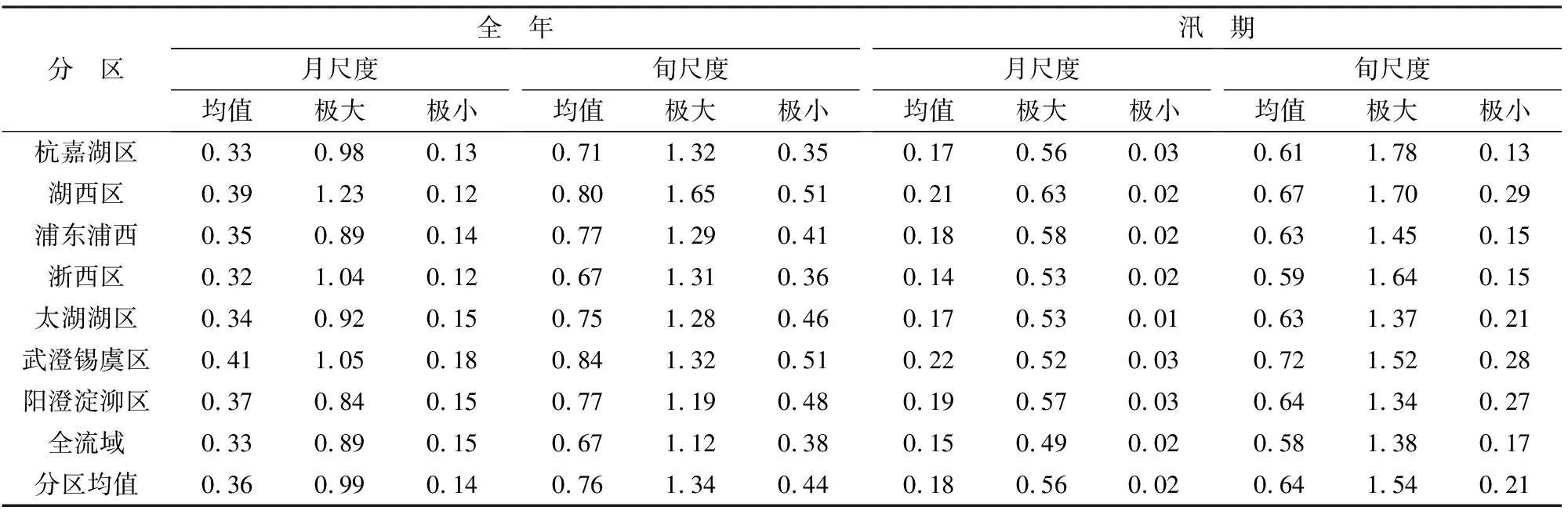
表2 各分区及全流域不同时间尺度下信息熵分配紊乱指数的特征值Tab.2 Feature values of ADI at different time scales for the whole basin and various drainage areas

表3 信息熵分配紊乱指数的Hurst，TFPW-MK和MK计算结果Tab.3 Calculated results of the Hurst，TFPW-MK and MK test for ADI

注：Z1表示TFPW-MK统计量；Z2表示MK统计量；H表示Hurst指数；加粗项为通过显著性检验值。其中，90%置信度为1.64，95%置信度为1.96。

4 结 语

基于1951—2011年太湖流域及各分区长系列降水资料，采用基尼系数、信息熵分配紊乱指数和变差系数分析了旬、月时间尺度上全年以及汛期降水时程分布的不均匀性。结果表明：ADI，GC和Cv这3种不均匀性指数的差异很小，相关系数可达0.93以上；太湖流域及各分区年内或汛期降水的不均匀性在年际间的差异较大，且北部武澄锡虞区和湖西区降水的年内分布不均匀性大于其他各分区；当降水量和指数值均较大时，流域较容易遭遇洪涝灾害，而在降水总量较小，不均匀性指数值较大时，则容易引发干旱灾害；在月尺度上，汛期降水不均匀性呈持续上升趋势，更加向6—8月集中，太湖流域遭遇洪涝的风险将加大。

此外，随着当前气候变化、人类活动的加剧以及流域城镇化进程的演进，区域性洪涝灾害愈加频繁。经分析表明武澄锡虞区和湖西区降水的年内分布不均匀性较大，凸显出降水空间分布的差异。因此，笔者认为有必要继续分析降水在空间上的不均匀性，以揭示降水在空间尺度上的分布差异，进一步为流域防灾减灾提供技术支撑。

参 考 文 献：

[1]许有鹏， 丁瑾佳， 陈莹. 长江三角洲地区城市化的水文效应研究[J]. 水利水运工程学报， 2009(4)： 67-73. (XU You-peng， DING Jin-jia， CHEN Ying. Impacts of urbanization on hydrology in the Yangtze River delta[J]. Hydro-Science and Engineering， 2009(4)： 67-73. (in Chinese))

[2]欧炎伦， 吴浩云. 1999年太湖流域洪水[M]. 北京： 中国水利水电出版社， 2001. (OU Yan-lun， WU Hao-yun. The Taihu basin flood of 1999[M]. Beijing： China WaterPower Press， 2001. (in Chinese))

[3]水利部太湖流域管理局. 太湖流域防洪规划[R]. 上海： 水利部太湖流域管理局， 2007. (Taihu Basin Authority of Ministry of Water Resources. Taihu basin flood control planning[R]. Shanghai： Taihu Basin Authority of Ministry of Water Resources， 2007. (in Chinese))

[4]王金星， 张建云， 李岩， 等. 近50年来中国六大流域径流年内分配变化趋势[J]. 水科学进展， 2008， 19(5)： 656-661. (WANG Jin-xing， ZHANG Jian-yun， LI Yan， et al. Variation trends of runoffs seasonal distribution of the six larger basins in China over the past 50 years[J]. Advances in Water Science， 2008， 19 (5)： 656-661. (in Chinese))

[5]梁进社， 孔健. 基尼系数和变差系数对区域不平衡性度量的差异[J]. 北京师范大学学报： 自然科学版， 1998， 34(3)： 409-413. (LIANG Jin-she， KONG Jian. Gini ratio and standard deviation： the difference of indicating regional disparity[J]. Journal of Beijing Normal University(Natural Science)， 1998， 34(3)： 409-413. (in Chinese))

[6]张录军， 钱永甫. 长江流域汛期降水集中程度和洪涝关系研究[J].地球物理学报， 2004， 47(4)： 622-630. (ZHANG Lu-jun， QIAN Yong-fu. A study of the feature of precipitation concentration and its relation to flood-producing in the Yangtze River valley of China[J]. Chinese Journal of Geophysics， 2004， 47(4)： 622-630. (in Chinese))

[7]SINGH V P. The use of entropy in hydrology and water resources[J]. Hydrological Processes， 1997， 11(6)： 587-626.

[8]MISHRA A K， ÖZGER M， SINGH V P. An entropy-based investigation into the variability of precipitation[J]. Journal of Hydrology， 2009， 370(1)： 139-154.

[9]刘新有， 史正涛， 彭海英， 等. 基于“基尼系数”的降水时间分布均匀度变化研究[J]. 气象研究与应用， 2007， 28(2)： 46-48. (LIU Xin-you， SHI Zheng-tao， PENG Hai-ying， et al. Study on precipitation temporal distribution homogeneous degree based on the Gini coefficient[J]. Journal of Meteorological Research and Application， 2007， 28(2)： 46-48. (in Chinese))

[10]王艳艳， 韩松， 喻朝庆， 等. 太湖流域未来洪水风险及土地风险管理减灾效益评估[J]. 水利学报， 2013， 44(3)： 327-335. (WANG Yan-yan， HAN Song， YU Zhao-qing， et al. The flood risk and flood alleviation benefit of land use management in Taihu basin[J]. Journal of Hydraulic Engineering， 2013， 44(3)： 327-335. (in Chinese))

[11]吴浩云， 王银堂， 胡庆芳， 等. 太湖流域61年来降水时空演变规律分析[J]. 水文， 2013， 33(2)： 75-81. (WU Hao-yun， WANG Yin-tang， HU Qing-fang， et al. Tempo-spatial change of precipitation in Taihu Lake basin during recent 61 years[J]. Journal of China Hydrology， 2013， 33(2)： 75-81. (in Chinese))

[12]王金南， 逯元堂， 周劲松. 基于GDP的中国资源环境基尼系数分析[J]. 中国环境科学， 2006， 26(1)： 111-115. (WANG Jin-nan， LU Yuan-tang， ZHOU Jing-song. Analysis of China resource-environment Gini coefficient based on GDP[J]. China Environmental Science， 2006， 26(1)： 111-115. (in Chinese))

[13]臧日宏. 经济学[M]. 北京： 中国农业大学出版社， 2002： 201-202. (ZANG Ri-hong. Economics [M]. Beijing： China Agriculture University Press， 2002： 201-202. (in Chinese))

[14]熊俊. 基尼系数估算方法的比较研究[J]. 财经问题研究， 2003(1)： 79-82. (XIONG Jun. A comparative analysis of appraisal method of Gini coefficient[J]. Research on Financial and Economic Issues， 2003(1)： 79-82. (in Chinese))

[15]张建华. 一种简便易用的基尼系数计算方法[J]. 山西农业大学学报： 社会科学版， 2007， 6(3)： 275-283. (ZHANG Jian-hua. An convenient method to calculate Gini coefficient[J]. Journal of Shanxi Agricultural University(Social Science Edition)， 2007， 6 (3)： 275-283. (in Chinese))

[16]许继军. 分布式水文模型在长江流域的应用研究[D]. 北京： 清华大学， 2007. (XU Ji-jun. Application of a distributed hydrological model to the Yangtze River basin[D]. Beijing： Tsinghua University， 2007. (in Chinese))

[17]BAYAZIT M， ÖNÖZ B. To prewhiten or not to prewhiten in trend analysis?[J]. Hydrological Sciences Journal， 2007， 52(4)： 611-624.