混凝土中钢筋锈蚀产物模量特性研究
徐 港,鲍 浩,王 青,2,徐浩铭
(1. 三峡大学土木与建筑学院,湖北宜昌 443002; 2. 三峡地区地质灾害与生态环境湖北省协同创新中心,湖北宜昌 443002)
钢筋锈蚀是影响混凝土结构耐久性的首要原因,与之相关的研究受到人们广泛重视[1-4]。目前关于锈蚀对混凝土结构抗力性能影响的研究已取得大量成果,然而对于锈蚀物自身力学性能的研究却仅有少量报道,如S.Kumiko等[5]绘制了锈蚀产物体积膨胀率-弹性模量关系图,认为钢筋锈蚀物的弹性模量值应在0.1~0.5 GPa之间;K.Lundgren[6]基于锈蚀导致混凝土保护层胀裂的仿真分析,推算得到铁锈的弹性模量Er值约为14.0 GPa;而S.Caré[7]等采用弹性理论对保护层锈蚀胀裂分析表明铁锈弹性模量为0.14 GPa;A.Ouglova[8]将锈样研磨成粒径为0.4~8.7 μm的锈粉,通过固结试验分析得到锈样加载稳定阶段的弹性模量为0.5 GPa;B.J.Pease[9]等通过数字图像技术,观察由于锈蚀产物体积膨胀引起的砂浆和钢筋界面的变形,与仿真分析得到的变形进行对比,得到了钢筋锈蚀产物的弹性模量在2.0 ~20.0 GPa之间;而I.Petre-Lazar和B.Gerard[10]采用划痕法测试铁锈力学性能,认为它是一种非黏性组合的不可压缩体;赵羽习和任海洋[11-12]基于改进的固结试验,运用Hertz弹性接触理论对铁锈模量进行研究,结果表明随荷载增加铁锈的瞬时弹性模量逐渐增大,铁锈不是弹性物质。令人遗憾的是,已有研究结论的差异很大,这一方面说明问题的复杂性,另一方面可能与不同学者所采用的方法和试样成分有关。
本文采用固结试验着重研究了锈蚀产物成分、粒径大小及分布对其压缩模量的影响特性,并论证推测了混凝土保护层锈胀开裂时的铁锈弹性模量的取值范围。希望所得结果能为钢筋锈蚀导致混凝土开裂分析参数选取提供参考。
1 试验设计
从三峡大学生命科学楼和逸夫楼楼顶钢架除锈锈块中收集锈样2组,分别命名为S和Y锈样,测得S锈样的密度为4.188 g/cm3,Y锈样密度为4.046 g/cm3。采用X射线衍射仪与EDS能谱分析仪分别对两种锈样成分进行分析,结果见图1和表1。结果表明自然锈蚀产物与钢筋混凝土锈胀生成的锈蚀产物成分[3,15]类似,都主要含有Fe3O4和Fe2O3。

(a) S锈样X射线衍射图 (b) S锈样扫描电镜图 (c) S锈样能谱分析

(d) Y锈样X射线衍射图 (e) Y锈样扫描电镜图 (f) Y锈样能谱分析图1 S锈样与Y锈样成分分析Fig.1 Components analysis of S and Y rust samples

锈样编号主要成分锈样粒径范围/ mm粒径平均值/ mmS1S2S3S4FeO(OH)和Fe(OH)30.100~0.3200.1670.080~0.1000.0920.050~0.0800.0660.010~0.0500.035Y1Y2Y3Y4Fe3O4和Fe2O30.100~0.3200.1560.080~0.1000.0900.050~0.0800.0660.010~0.0500.0342#3#Fe3O4,Fe2O3和β-FeO(OH)0.100~0.2500.1220.075~0.1000.0605#6#Fe3O4,Fe2O3,α-FeO(OH)和β-FeO(OH)0.100~0.2500.1560.075~0.1000.061
注: 2#,3#,5#,6#锈样取自文献[12]。
将S和Y锈块晒干、碾磨为粉状,用定制孔径为0.050,0.080和0.100 mm的3种网筛在水泥细度负压筛析仪上分别对两种锈样进行筛分(图2),得到粒径范围为0.010~0.050 mm,0.050~0.080 mm,0.080~0.100 mm和0.100~0.320 mm的4类锈粉,分别编号为S1,S2,S3,S4和Y1,Y2,Y3,Y4(两组锈样取自不同地方,即两种锈样化学成分不同)。对每组锈样按粒径大小再细划分为10个小区间,随机取200个颗粒采用KH7700数字显微镜进行粒径测量(图3),并统计落入每个小区间内的个数,得到各试样粒径分布(图4)。由于每一个锈样颗粒在各个方向上的尺寸并不相同,取其最大值为粒径测量值。
设每种试样各细分小区间粒径平均值为rii,个数为ni,则由ri=∑riini/200可求得该组试样粒径平均值(ri)。最终求得各试样粒径平均值分别为:rS1=0.167 mm,rS2=0.092 mm,rS3=0.066 mm,rS4=0.035 mm;rY1=0.156 mm,rY2=0.090 mm,rY3=0.066 mm,rY4=0.034 mm。

(a) 锈块碾磨 (b) 网筛选择 (c) 锈样筛分 (d) 筛分获得的锈样图2 筛分试验Fig.2 Screening tests

(a) 待测锈样 (b) 粒径观测 (c) 观测结果图3 粒径观测试验Fig.3 Particle size observation tests

(a) S1,Y1锈样粒径分布 (b) S2,Y2锈样粒径分布
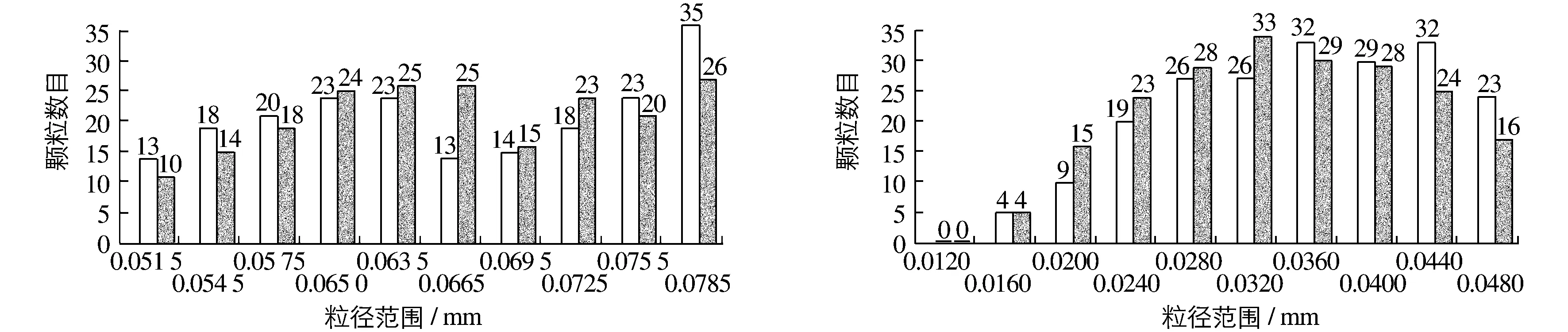
(c) S3,Y3锈样粒径分布 (d) S4,Y4锈样粒径分布图4 各组锈样粒径分布Fig.4 Particle size distribution of rust samples groups
2 锈样的固结试验
参考《土工试验方法标准》(GBT 50123-1999),采用WG-2A双联固结仪对锈样进行固结试验,为提高计数的精度,采用数显千分表读数。通过预做试验发现每级荷载施加15 min后读数变化趋缓,故本试验每15 min读数1次。以S1试样为例,固结试验过程如图5,具体操作步骤如下:
(1)安装好固结试验仪,将环刀C固定在固结试验仪上;
(2)将锈样取120 g倒入环刀C内进行分层预压,使环刀正好填满;

图5 固结试验过程Fig.5 Oedometer test process
(3)将千分表固定在固结仪上,调整并记录好千分表的初始读数;取2.552 kg(=100 kPa)的砝码置于固结仪上,对S1进行第1级加载,每级加载后的千分表读数记为该级0点值,此后每隔15 min读取一次千分表读数,分别记为1,2,3,4点读数,并进入下一个荷载施加阶段;
(4)依照上述步骤,依次在S1锈样上施加100,150,200,250,300,350,400和450 kPa共8级荷载,并记录变形量Δ。
重复上述试验过程,控制锈样质量相等,依次完成S2,S3,S4和Y1,Y2,Y3,Y4等其余7组锈样的固结试验。
3 试验结果及分析
基于固结试验原理,可由下式(1)求得到锈样在各级外荷载作用下的压缩量Ec的大小:
(1)
式中:h为环刀高度;Δhi+1为第(i+1)级加载的压缩量;∑Δhi为前i级加载的累计压缩量;(Pi+1-Pi)为相邻两级荷载差。
将S,Y组锈样固结试验数据代入式(1),得到S(S1,S2,S3,S4)和Y(Y1,Y2,Y3,Y4)锈样的荷载-压缩模量关系,如图6(a)和(b),可知:外荷载范围在100~450 kPa之间时,钢筋混凝土锈蚀产物的压缩模量变化范围为4~45 MPa,铁锈的压缩模量值随着荷载增大而线性增大,并非一个定值。分析其原因可能与土颗粒类似,锈样颗粒间含有大量的孔隙,当它承受的轴向荷载增加时,随着深度的增加会引起水平压力的增大,铁锈颗粒趋渐密实,此时铁锈的抗变形能力也有所加强,压缩模量增大[13-14]。文献[12]进行了与本文类似的试验,所采用锈样基本信息见表1中的2#,3#,5#,6#锈样,对其试验结果进行分析也得到相似关系,如图6(c)和(d)。但是,值得注意的是粒径和成份不同锈样的荷载-压缩模量线性拟合式的斜率并不相同。

(a) S组锈样 (b) Y组锈样

(c) 2#和3#锈样 (d) 5#和6#锈样图6 锈样荷载-压缩模量关系曲线Fig.6 Relation curves of load-compression modulus of rust samples in oedometer tests
为此,取S1,Y1,2#及5#等4种平均粒径接近但化学成分不同的锈样进一步分析,如图7(a),可见在相同加载条件下,各试样荷载-压缩模量拟合直线的斜率由大到小顺序为S1>5#>2#>Y1,而锈样按氧化程度由大到小排序为Y1>2#>5#>S1,同理分析S3,Y3,3#及6#锈样也可以得到相同的规律,如图7(b),说明锈蚀物氧化越充分,其压缩模量值随荷载增加变化幅度越小。分析原因可能是由于不同锈蚀物和微观组织结构不同造成的,如图1(b)和(e),Y组锈样较S组的微观结构更为密实。

(a) 锈样S1,Y1,2#及5# (b) 锈样S3,Y3,3#及6#图7 锈样荷载-压缩模量关系曲线Fig.7 Relation curves of load-compression modulus of rust samples in oedometer tests
取化学成分相同而平均粒径不同试样进行分析,如图8。由图可见:(1)对于同种锈样,各级荷载作用下,锈样平均粒径与压缩模量间的关系具有相似变化规律;(2)对于不同锈样,同级荷载下平均粒径与压缩模量间的关系差异较大,无明显规律,有待进一步研究。

(a) S锈样 (b) Y锈样

(c) 2#和3#锈样 (d) 5#和6#锈样图8 锈样粒径与压缩模量关系曲线Fig.8 Relation curves of particle size-compression modulus of rust samples
4 锈蚀产物弹性模量推测
有学者[16]曾通过理论分析得到钢筋锈蚀导致混凝土构件保护层表面胀裂时的最大锈胀力:
(2)
式中:ft为混凝土轴心抗拉强度平均值;c为混凝土保护层厚度;r为钢筋半径。
考虑到环境的差异,设混凝土强度等级变化范围为C20~C50、保护层厚度变化范围为20~50 mm,纵向受力钢筋直径取10~40 mm,对这3类变量进行不同组合,按式(2)求解,汇总求解结果后可知最大锈胀力为0.75~11.32 MPa。将锈胀力上、下限值代入不同锈样的荷载-压缩模量拟合方程(图6中各数据拟合式),可得与之相应的锈蚀物压缩模量值为21.16~880.27 MPa。
如假定锈样为弹性材料,根据材料力学理论,可知弹性模量E0和压缩模量Ec之间存在如下关系:
(3)
式中:μ为锈蚀物的泊松比。
目前,对锈蚀物泊松比的取值尚存在争议,本文取μ为0.25[17],代入式(3)可得:E0=0.833Ec。将上述得到的保护层胀裂时的压缩模量代入到式(3)中,可得锈蚀物的弹性模量值(E0)为0.017~0.733 GPa。
5 结 语
采用水泥细度负压筛分仪得到4种不同粒径范围的锈样,通过固结试验研究其压缩模量值的变化规律,得出:
(1)锈蚀物压缩模量随着压应力增加而增大,非定值,但两者线性相关。
(2)相同应力水平,粒径相近锈样的压缩模量大小与锈蚀物化学成分相关,锈蚀物氧化越充分,其压缩模量值随压应力增加变化幅度越小。
(3)钢筋混凝土构件保护层表面锈胀开裂时,锈蚀物弹性模量值为0.017~0.733 GPa。
参 考 文 献:
[1]徐港, 卫军. 钢筋均匀锈胀力的若干问题研究[J]. 福州大学学报: 自然科学版, 2005, 33(增1): 101-105. (XU Gang, WEI Jun. Research on corroded expansive force of the concrete reinforced bar[J]. Journal of Fuzhou University(Natural Science), 2005, 33(Suppl1): 101-105. (in Chinese))
[2]余江, 赵羽习, 金伟良. 混凝土结构锈胀裂缝中铁锈分布的试验研究[J]. 混凝土, 2011(3): 5-8. (YU Jiang, ZHAO Yu-xi, JIN Wei-liang. Experimental study on distribution of corrosion products in corrosion-induced cracks in reinforced structures[J]. Concrete, 2011(3): 5-8. (in Chinese))
[3]姬永生, 袁迎曙, 宋萌, 等. 不同锈蚀条件下混凝土内钢筋锈蚀物膨胀性能比较和机理分析[J]. 北京工业大学学报, 2011, 37(11): 1677-1683. (JI Yong-sheng, YUAN Ying-shu, SONG Meng, et al. Volume expansion characteristic and mechanism of rebar corrosion products in concrete with different corrosion approaches[J]. Journal of Beijing University of Technology, 2011, 37(11): 1677-1683. (in Chinese))
[4]金伟良, 赵羽习, 鄢飞. 钢筋混凝土构件的均匀钢筋锈胀力的机理研究[J]. 水利学报, 2010(3): 58-60. (JIN Wei-liang, ZHAO Yu-xi, YAN Fei. The mechanism of corroded expansion force of reinforced concrete members[J]. Journal of Hydraulic Engineering, 2010(3): 58-60. (in Chinese))
[5]KUMIKO S, SUDHIR M, KENICHI M. Corrosion products of reinforcing bars embedded in concrete[J]. Corrosion Science, 1993, 35(5-8): 1543-1549.
[6]LUNDGREN K. Bond between ribbed bars and concrete. Part 2: The effect of corrosion[J]. Magazine of Concrete Research, 2005, 57(7): 383-395.
[8]OUGLOVA A, FRANCOIS M, BERTHAUDY, et al. Mechanical properties of an iron oxide formed by corrosion in reinforced concrete structures[J]. Corrosion Science, 2006, 48(12): 3988-4000.
[9]PEASE B J, MICHEL A, THYBO A E A, et al. Estimation of elastic modulus of reinforcement corrosion products using inverse analysis of digital image correlation measurements for input in corrosion-induced cracking model[C]∥6thInternational Conference on Bridge Maintenance, Safety and Management (IAMBAS), Lake Como, Italy, 2012.
[10]PETER-LAZAR I, GERARD B. Mechanical behavior of eorrosion products formed at the steel-concrete interface[C]∥Fourteenth Engineering Mechanics Conferenee, ASCE, Austin, 2000.
[11]赵羽习, 任海洋. 基于固结实验和接触理论分析的铁锈力学性能[J]. 中国腐蚀与防护学报, 2010, 30(5): 383-390. (ZHAO Yu-xi, REN Hai-yang. Mechanical behavior of the rust based on oedometer test and Hertz contact theory[J]. Journal of Chinese Society for Corrosion and Protection, 2010, 30(5): 383-390. (in Chinese))
[12]任海洋, 赵羽习. 不同环境下钢筋锈蚀产物的力学性能研究[D]. 杭州: 浙江大学, 2010. (REN Hai-yang, ZHAO Yu-xi. Study on mechanical behavior of corrosion products under different environments[D]. Hangzhou: Zhejiang University, 2010. (in Chinese))
[13]牟春梅, 李佰锋. 外荷载作用下软土压缩模量动态演化规律[J]. 土木建筑与环境工程, 2009, 31(4): 49-54. (MU Chun-mei, LI Bai-feng. Dynamic evolution pattern of compression modulus of soft clay[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(4): 49-54. (in Chinese))
[14]周翠英, 林春秀, 林鲁生, 等. 外荷载作用下软土压缩模量的动态演化规律研究[J]. 岩土力学, 2010, 31(7): 2040-2044. (ZHOU Cui-ying, LIN Chun-xiu, LIN Lu-sheng, et al. Research on dynamic evolution law of compression modulus of soft clay under external loads[J]. Rock and Soil Mechanics, 2010, 31(7): 2040-2044. (in Chinese))
[15]温婷. 钢筋混凝土构件通电锈蚀试验适用性研究[D]. 宜昌: 三峡大学, 2014. (WEN Ting. Applicability study on electrifying corrosion methods of reinforced concrete members[D]. Yichang: China Three Gorges University, 2014. (in Chinese))
[16]XU Gang, WEI Jun, ZHANG Ke-qiang, et al. A calculation model for corrosion cracking in R.C. structures[J]. Journal of China University of Geosciences, 2007, 18(1): 85-89.
[17]戴虹. 混凝土结构中的钢筋锈蚀产物力学性能研究[D]. 杭州: 浙江大学, 2012. (DAI Hong. Study on mechanical performance of corroded steel bars in concrete structures[D]. Hangzhou: Zhejiang University, 2012. (in Chinese))

