连续梁拱组合体系桥梁地震反应分析

(苏州市慧杰工程设计有限公司，江苏 苏州 215011)

1 桥梁概况

桥梁结构为 (33+55+33)m的下承单承载面拱梁组合结构，采用整幅断面，断面宽度为24.0 m，其总体布置图见图1所示。下设置三个抗震型盆式橡胶支座。

2 模型建立

2.1 边界条件的模拟

结构稳定分为两类，第一类稳定叫做平衡分支失稳，即到达临界荷载时，除结构原来的平衡状态外，理论上仍可能出现第二个平衡状态；第二类是极值点失稳，结构保持一个平衡状态，随着荷载的增加在应力比较大的区域出现塑性变形，结构变形很快增大，当荷载达到一定数值时，即使不再增加，结构变形也自行迅速增大以至于结构破坏[1-2]。

地震荷载作用下，支座的水平刚度对桥梁主体结构的地震反应影响较大，因而为了反映地震时桥梁结构的实际受力情况，在做桥梁抗震分析时应准确模拟支座的水平刚度[2-4]。

计算分析中一般将活动支座简化为摩擦单元，其恢复力简化为理想的双线性模型。若支座的支反力为FN，滑动摩擦系数为μ，K为支座的初始剪切刚度，支座在滑动后的剪切刚度为0，xy为屈服位移，则初始刚度K=μFN/xy，活动支座的恢复力模型如图2所示。

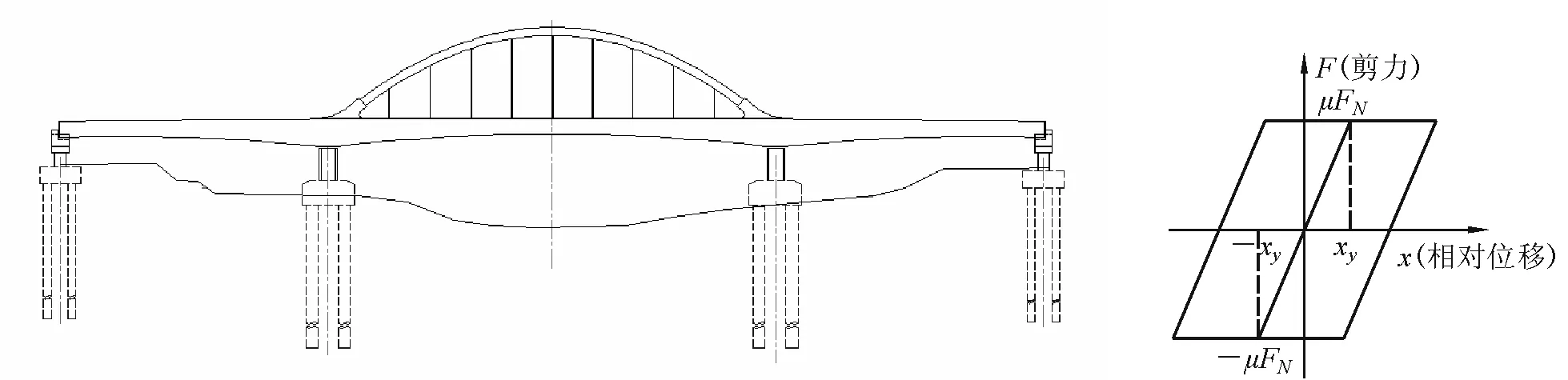
图1 总体布置图 图2 活动支座恢复力模型

试验结果表明板式橡胶支座恢复力模型呈狭长型[5]，因而一般可做线性处理；活动盆式橡胶支座一般简化为图2所示理想恢复力模型；抗震型固定盆式橡胶支座及单向活动支座的非活动方向亦可以发生滑动，其发生滑动的临界力为竖向支反力的20%，以降低地震作用传递到下部结构的剪力，从而起到保护桥梁下部结构的作用，故抗震型固定盆式橡胶支座及单向活动支座的非活动方向恢复力模型亦采用图2所示理想双线性模型。

2.2 模型的建立

计算模型主要着重模拟结构的刚度、质量和边界条件，其中吊杆采用桁架单元模拟，主梁、拱肋、桥墩、承台及桩基均采用三维梁单元模拟。模型中通过在桩基础相应位置处设置纵、横桥向土弹簧的方法，来考虑桩土相互作用的影响，且仅考虑土弹簧刚度，忽略阻尼和质量特性的影响，弹簧刚度根据m值法进行计算输入。引桥作用通过在边墩上施加支座集中力来模拟，引桥板式支座通过线性弹簧模拟，主桥盆式支座通过非线性摩擦单元模拟。主桥三维有限元模型如图3所示。桥梁有限元分析考虑如下工况：

设计工况：按实际情况同时考虑引桥作用及抗震支座作用；

比较工况1：考虑引桥作用，不考虑抗震支座作用(改为普通盆式支座)；

比较工况2：考虑抗震支座作用，不考虑引桥作用。

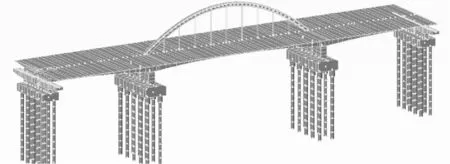
图3 连续梁拱组合体系桥梁三维有限元模型

3 动力特性分析

分析和认识大跨桥梁的动力特性是进行地震反应分析和抗震设计的基础[6]。在上述连续梁拱组合桥梁模型的基础上，采用多重Ritz向量法，计算桥梁结构的动力特性。表1列出了该桥的前10阶振型的频率及振型特征，其中频率1、频率2、频率3及编号①②③分别对应设计工况、比较工况1、比较工况2。其对应的前4阶振型如图4所示。

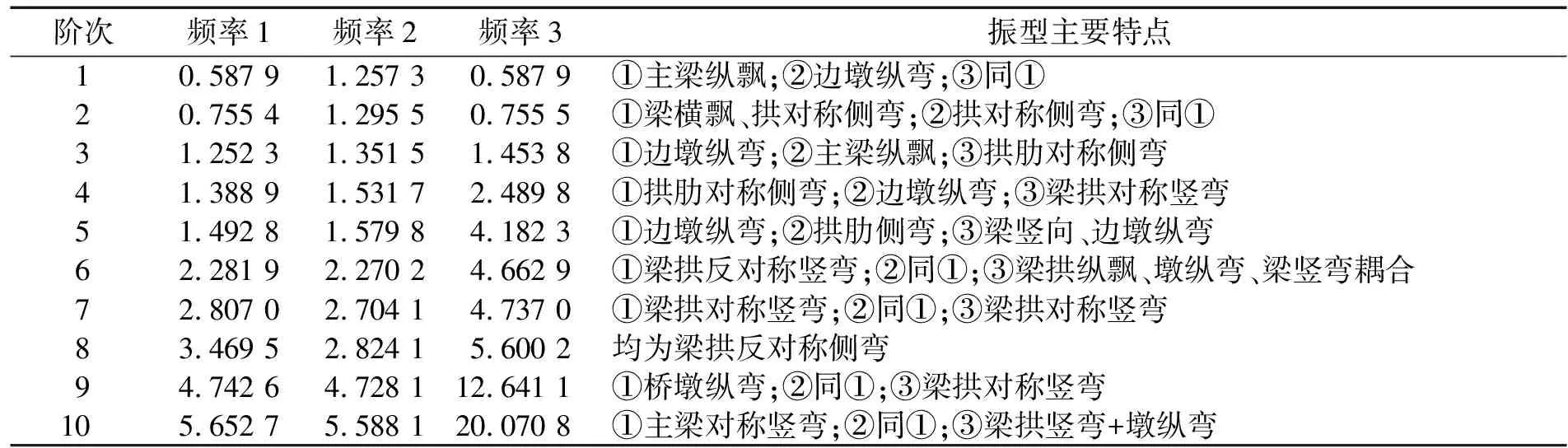
表1 结构动力特性表 Hz

由上述动力分析结果知，采用抗震支座后结构基本周期为采用普通盆式支座结构的两倍以上；由于考虑了引桥对边墩的作用，边墩纵弯振型提早出现；设计工况下全桥一阶纵向振型为上部结构纵飘，一阶横向振型为梁横飘、拱对称侧弯，体现了考虑抗震支座影响后，桥梁的支座刚度相对较低，地震时可起减隔震作用；全桥竖向振型出现较迟。

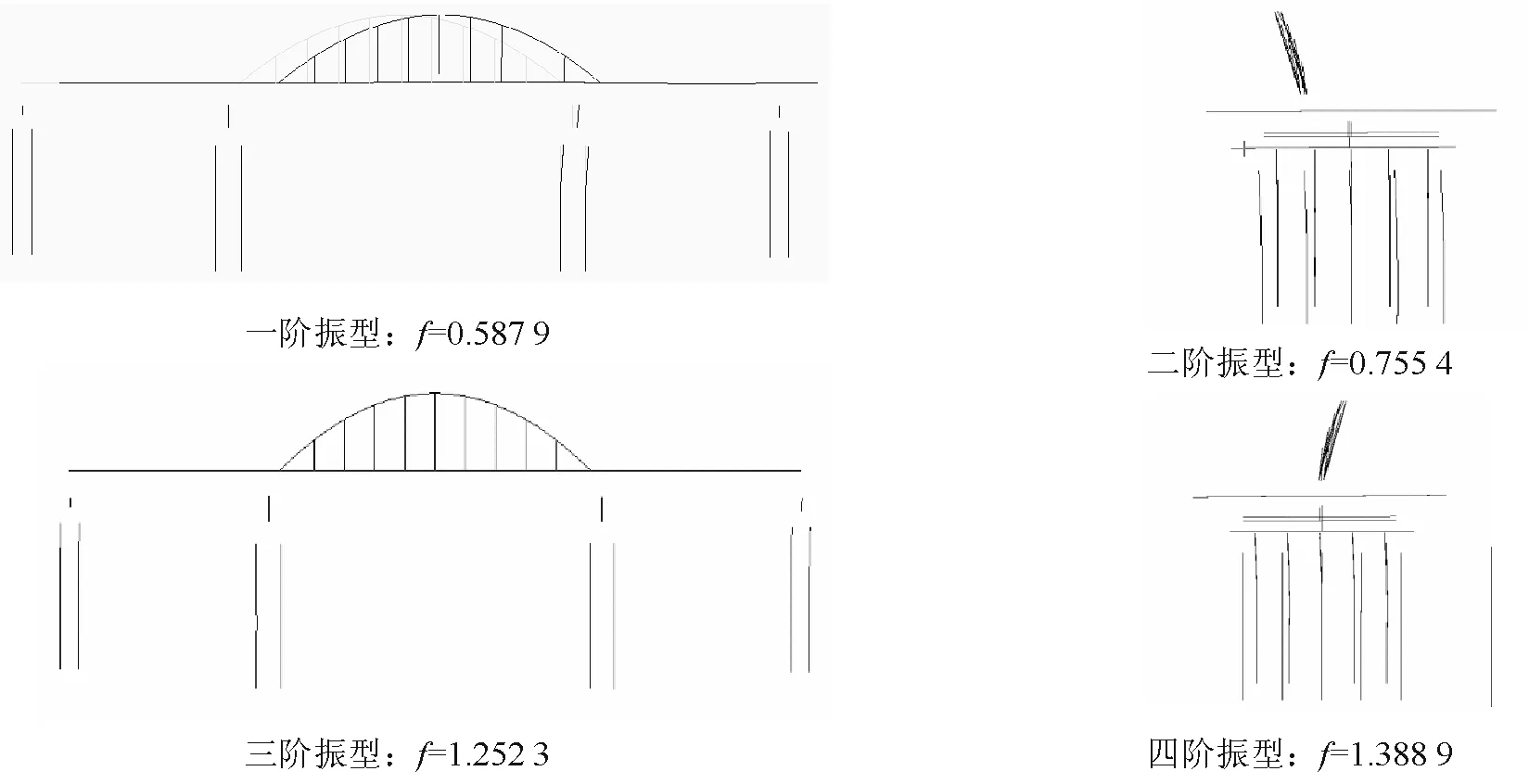
图4 设计工况下主桥前4阶振型图

4 反应谱法地震反应分析

反应谱法在当前结构抗震设计中广泛使用，采用反应谱法进行桥梁结构抗震计算，只需取少数几个低频振型就能够取得满意的结果。本桥场地类型为Ⅲ类场地，抗震设防烈度为7度，参照《公路桥梁抗震设计细则》(JTG/T B02—01—2008)，确定其E2地震下反应谱曲线如图5所示。

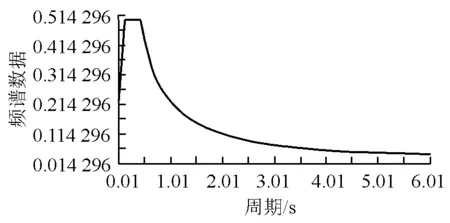
图5 地震反应谱曲线

进行反应谱计算时，特征值分析采用多重Ritz向量法，取结构前30阶振型，使结构在X、Y、Z方向的振型参与质量均达到90%以上。结构阻尼比取0.05，振型组合采用CQC法。由反应谱分析所得桥梁墩底剪力及墩顶位移值如表2～表3所示。分析可知：

(1)在纵桥向输入反应谱，66.7%的墩底剪力集中在3#墩，主要原因是3#墩顶设置纵桥向固定支座，而1#、2#、4#墩顶设置纵桥向滑动支座；从另一角度来看，由于考虑了滑动支座的滑动刚度及引桥板式支座的刚度，故1#、2#、4#墩分担了33.3%的纵向地震力，一定程度上减轻了3#墩所承受的纵向地震力。

(2)在横桥向输入反应谱，2#、3#墩墩顶位移及墩底剪力基本相同；1#、4#墩墩顶位移及墩底剪力基本相同，主要是因为横桥向2#、3#墩支座横向刚度及桥墩刚度基本相同；1#、4#墩支座横向刚度及桥墩刚度基本相同。

(3)与比较工况1相比，设计工况下3#固定墩墩底最大剪力由22 309 kN降低至8 564 kN，若定义减震率为不考虑抗震支座影响结构反应与考虑抗震支座影响结构反应的差值，占不考虑抗震支座影响结构反应的百分数，则采用抗震支座后，固定墩纵向减震率达62%，横向减震率达60%。

(4)根据反应谱计算结构内力，结构强度满足要求，反应谱地震作用下梁体最大位移96.5 mm，不会发生落梁危险。

表2 谱分析桥梁墩底最大剪力值 kN

注：表中括号内数字为比较工况1下固定墩的数值，括号外为设计工况下数值。

表3 谱分析桥梁墩顶最大位移值 mm

5 时程法地震反应分析

由于反应谱不能考虑结构边界的非线性问题，而且仅能给出各振型的最大值，即使结构处于弹性状态，反应谱也不能完全代替时程分析方法[7]，因此有必要对该桥进行时程分析。对该桥进行时程分析时，采用中国天津(1976)地震波记录、lwd-DEL AMO BLVD., LAKEWOOD, CA,COMP N00E和南京地震波三条与本工程所在场地相近的地震波记录。

进行时程分析时，需要将加速度时程曲线幅值与地震基本烈度相对应[1]，地震基本烈度取0.1g，计算中对实际的地震波按下式进行修正

(1)

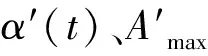
图6 修正后地震波曲线

时程分析在不同地震动输入时墩底最大剪力及墩顶最大位移分别列于表4及表5，由此可以看出：

(1)与反应谱法所得结果趋势相同，在纵向时程波作用下，桥墩剪力主要集中在3#墩；在横向时程波作用下，2#、3#墩墩顶位移及墩底剪力基本相同；1#、4#墩墩顶位移及墩底剪力基本相同。

(2)与反应谱法相比，时程分析法所得固定墩纵向墩底剪力减小了31%，横向墩底剪力减小了41%。主要原因是时程分析法考虑了边界非线性问题。地震力引起的支座水平力已经超出了抗震支座的水平承载力，故固定抗震支座已经开始滑动。抗震固定支座的滑动降低了传递到下部结构的剪力，从而起到保护桥梁下部结构的作用。同时，由于固定抗震支座的滑动摩擦耗能作用，降低了结构的地震响应，因而时程法求得的位移较反应谱法求得的位移小，梁体在天津波作用下的位移响应如图7所示。

(3)与比较工况2相比，考虑引桥作用后，1#、4#边墩墩底剪力增大了2～5倍，其主要原因是在模型中主桥边墩活动抗震盆式支座按非线性弹簧模拟，在地震力作用下，主梁边墩支座的滑动降低了传递到边墩的水平剪力，而引桥板式橡胶支座按线弹簧模型模拟，引桥地震力均传递到边墩。设计工况下边墩墩底剪力的增大部分主要是由引桥引起，这一点在动力特性分析中设计工况下边墩纵向振型提早出现也可以看出，如图4。

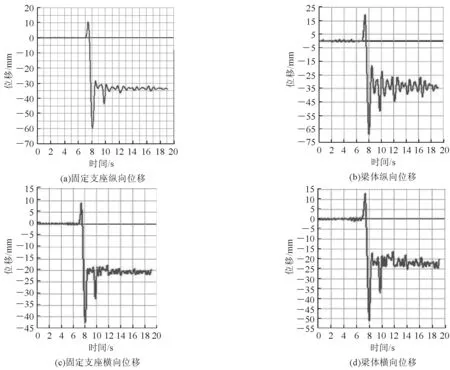
图7 天津波作用下固定支座及梁体位移图

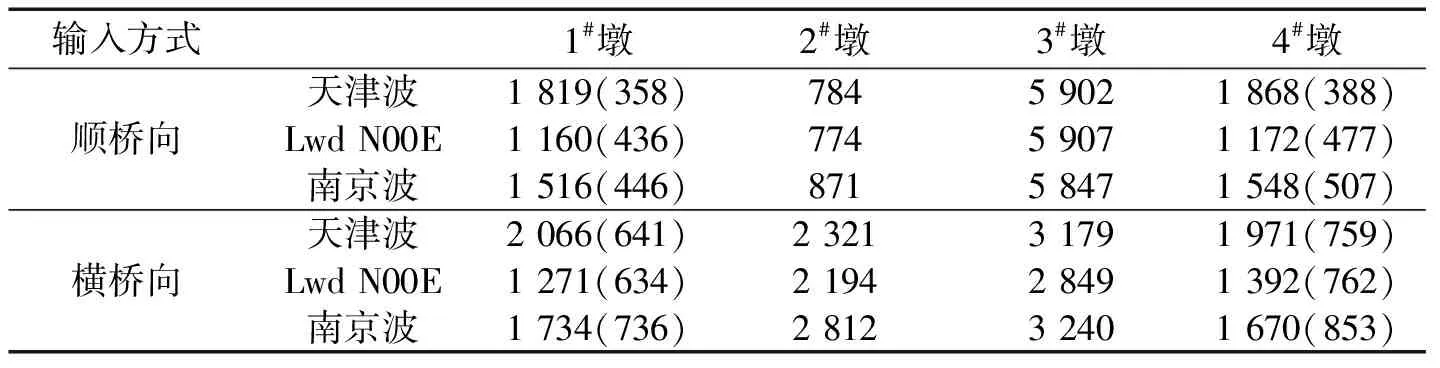
表4 时程法分析桥墩底最大剪力 kN

注：括号内数字为不考虑引桥作用的墩底剪力。

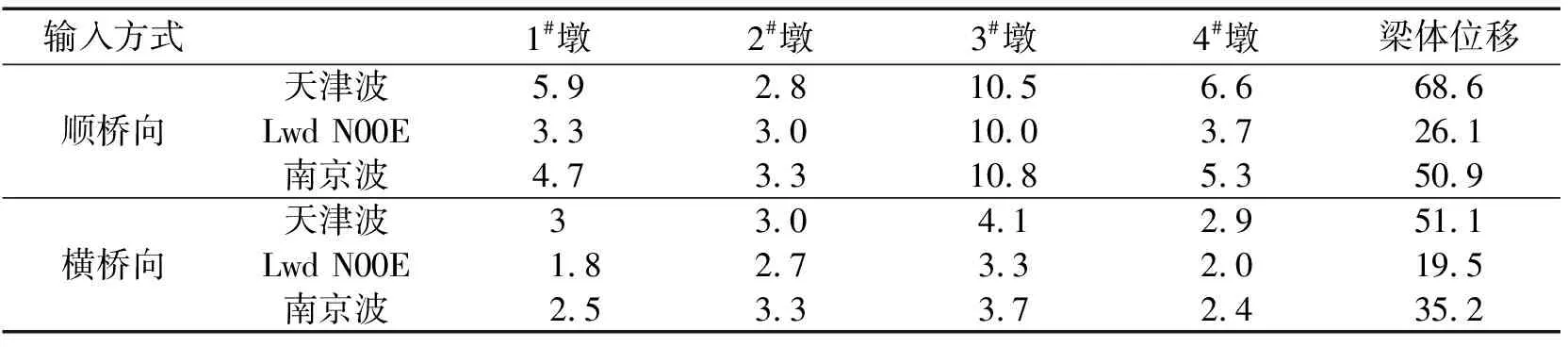
表5 时程分析桥梁墩顶最大位移 mm

6 结论

对连续梁拱组合体系桥梁进行了动力特性分析、反应谱法地震反应分析、时程法地震反应分析，通过分析比较得出了一些对工程设计有参考价值的结论，主要总结如下：

(1)地震作用下，应考虑滑动支座滑动刚度的影响。滑动支座所在桥墩将会分担一部分剪力，从而一定程度上减轻固定墩墩底剪力，使得结构设计更合理。

(2)采用抗震支座后桥梁的减震效果明显。考虑抗震支座影响后，连续梁拱组合体系桥梁的减震率达62%，根据反应谱计算，抗震强度满足要求，反应谱法地震作用下梁体最大位移96.5 mm，不会发生落梁危险。

(3)时程法可以考虑结构边界的非线性问题，更能反应结构在地震时的实际反应情况。通过时程法进行分析，固定抗震支座已经开始滑动，固定抗震支座的滑动降低了传递到下部结构的剪力，从而起到保护桥梁下部结构的作用。同时，固定抗震支座的滑动摩擦耗能作用降低了结构的地震响应。

(4)考虑抗震支座的减隔震影响后，本桥基本周期延长了两倍以上；由于考虑了引桥对边墩的影响，边墩纵弯振型提早出现，这说明在地震作用下边墩地震力较大，因本桥边墩刚度较大，不控制设计，但对于边墩刚度较小的桥梁应引起注意。

参 考 文 献

[1]王松涛,曹资.现代抗震设计方法[M]．北京：中国建筑工业出版社，1997.

[2]王常峰,陈兴冲,朱东生.活动支座摩擦力对桥梁抗震性能的影响参数分析[J]. 世界地震工程,2005(4):82-87.

[3]韦晓,袁万城.关于桥梁抗震设计规范反应谱若干问题[J]. 同济大学学报：自然科学版,1999,27(2):16-19.

[4]叶章旺.考虑活动支座摩擦力的连续梁桥抗震性能分析[J]. 路基工程,2009(3):112-113.

[5]李立峰,吴文朋,黄佳梅,等.板式橡胶支座地震易损性分析[J]. 湖南大学学报:自然科学版,2011,38(11):1-6.

[6]范立础.桥梁抗震[M]．上海：统计大学出版社，1996.

[7]郑国栋,李校兵.不同方法对某桥梁抗震分析的影响比较[J]. 公路,2010(3):60-65.