基于非结构网格的风压分配方法
, , ,
(石家庄铁道大学 风工程研究中心,河北 石家庄 050043)
0 引言
由于模型制作简单、测试得到的信息丰富、测试技术成熟等原因,刚性模型测压风洞试验是目前建筑结构抗风设计最常用的试验方法之一[1-3]。刚性模型测压试验得到了大量的测点数据,将这些数据直接用于结构设计中存在一定的困难,主要是由于风荷载测试中的测点分布与结构设计中的荷载输入要求不匹配,因此需要将刚性模型测压试验得到的结果按照不同层面的需求进行处理[4],如分块体型系数、不同侧面的风荷载、结构整体力系数、按照动力计算模型输入的节点风荷载、按照模态输入的模态力谱等[5]。
刚性模型测压试验得到的是结构表面各个位置的风压时程,将这种风压时程直接用于设计结构风荷载时面临的最大问题是:针对考察问题的不同,需要将这些风压时程做不同的处理。一般情况下测点分布无法满足要求,例如将测点风压时程转化为结构节点上的风荷载时,往往由于测点的分布过于稀疏无法获得各个节点的风荷载或者获得的风荷载在较大区域内的节点上的风荷载是相同的,这可能会对结构风致振动的分析带来误差;再例如将测点的风压时程转化为便于结构设计输入的分块风荷载参数如分块体型系数时,每个测点所代表的面积权值比较难以确定,因为分块区域的划分往往会将某个测点的代表区域划分入不同的分块,这样的话每个分块中该测点的权值就需要单独进行面积计算,效率很低且准确性不高。
本文提出了一种新型的非结构化网格的风荷载处理方法,通过非结构化网格将结构表面测试得到的风压进行细化插值,可得到节点风荷载、分块风荷载及力系数等结构设计所需要的计算风荷载。该方法解决了结构风荷载匹配处理、风致响应计算等问题,得到的风荷载准确,自动化程度高。
1 非结构化网格处理方法
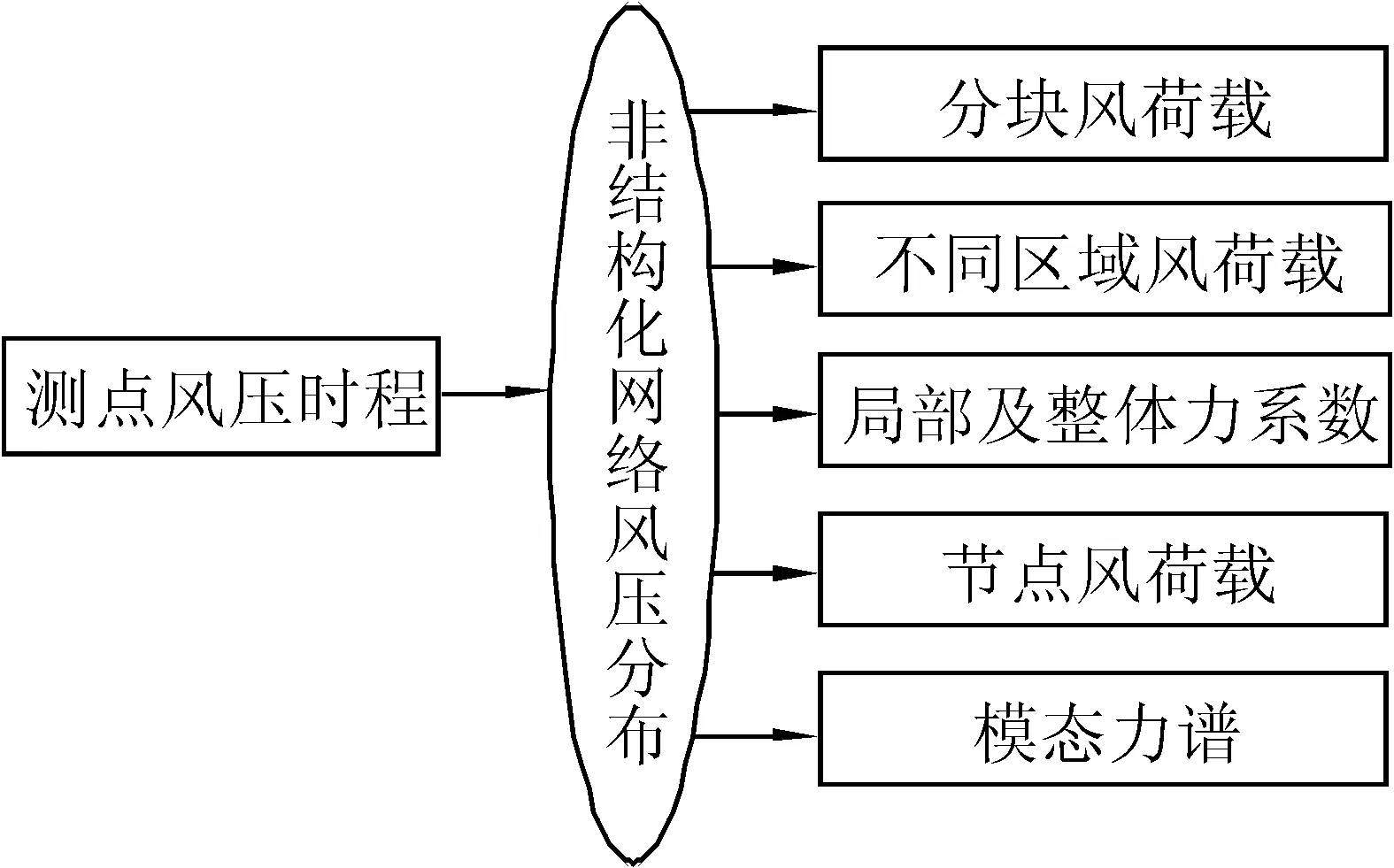
图1 非结构化网格处理示意图
图1为非结构化网格处理示意图,其基本思想是将测点的风压时程转换为非结构化网格的风压分布,这种风压分布密度要远高于测点风压分布的密度,其分布是以测点及其风压作为控制点的,这样既保证了网格风压分布的可靠性也保证了该风压分布用于进一步风荷载处理的准确性。
图2为非结构化网格划分示意图,通过网格的密化,来实现风压分布的精细化,从而为进一步进行风荷载分析提供精确的数据保障。

图2 非结构化网格划分
将非结构的单元网格节点相连组成非结构网格面(下文称为虚面),并为该面定义方向(右手坐标系逆时针旋转为正),给出了非结构化网格点构成虚面的过程。
N1、N2、N3对应的节点坐标由测点坐标插值得到(一般采用2~4次多项式分块插值得到),3个节点上对应的风荷载时程分别为P1、P2、P3,分别由测点风荷载按照坐标插值的规律插值得到,这样就将测点坐标及测点风压精细化了。
以Area1为例,该面由3个节点N1、N2、N3按照逆时针旋转组成,此时Area1的各种几何信息可以由组成它的3个节点坐标计算得到,如面积、方向、中心点坐标等等。同时也可以根据P1、P2、P33组风压时程取平均值得到Area1的风压时程。计算方法如下
(1)
式中,S1表示Area1的面积;f1表示该面的法向量;NA1为Area1的中心点坐标;PA1为作用在Area1上的风压。
一般风压测点无法布置在结构风压测试面的边界,因此需要构造边界节点,将曲线边界近似划分为多个与网格精度相当的直线段,直线段的端点作为边界节点,然后形成非结构单元的节点与虚面。
对于表面为单个连续曲面的结构,上述网格划分过程可以一次完成,当结构表面为多个非连续的曲面拼合而成时,需要对各个面进行独立的网格划分并将其组合,同时为了准确的将风荷载匹配到划分的网格节点上,风荷载也按连续面进行插值。
2 非结构化网格的应用实例
2.1 网格划分
某大跨度空间照片及网格划分图如图3所示,图3(b)中的网格划分图是以2 m作为网格点距离,图中较大黑点为测点,共280个,小黑点为采用非结构化网格对结构进行网格划分后得到三维的结构网格节点,共约36 765个,黑色区域为某测点对应的虚面组成的区域。
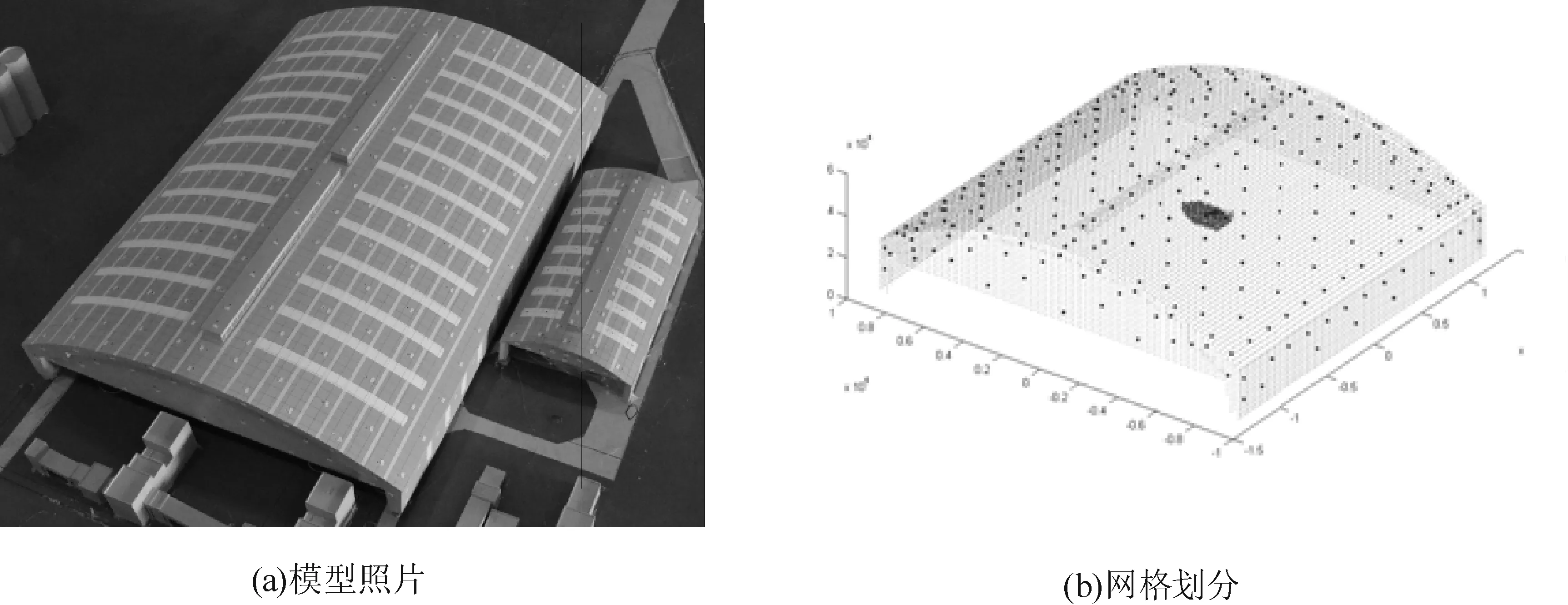
图3 某大跨度空间结构网格划分图
2.2 分块体型系数计算
通过结构边界与测点坐标插值得到的这些网格点可以有效的细化结构的风荷载分布,结合图3中细化的网格节点及面分布,可以进一步计算结构的分块体型系数。将结构划分为不同的分块如图4所示,利用非结构化网格技术,分别计算各个分块的体型系数,并根据不同风向角及工况下的体型系数变化判断最不利工况。
以L01分块为例,Max7、Min7、Max4、Min4 4种工况、不同风向角下的体型系数如图5。由图5可以看出,体型系数最值发生的工况及对应的风向角。
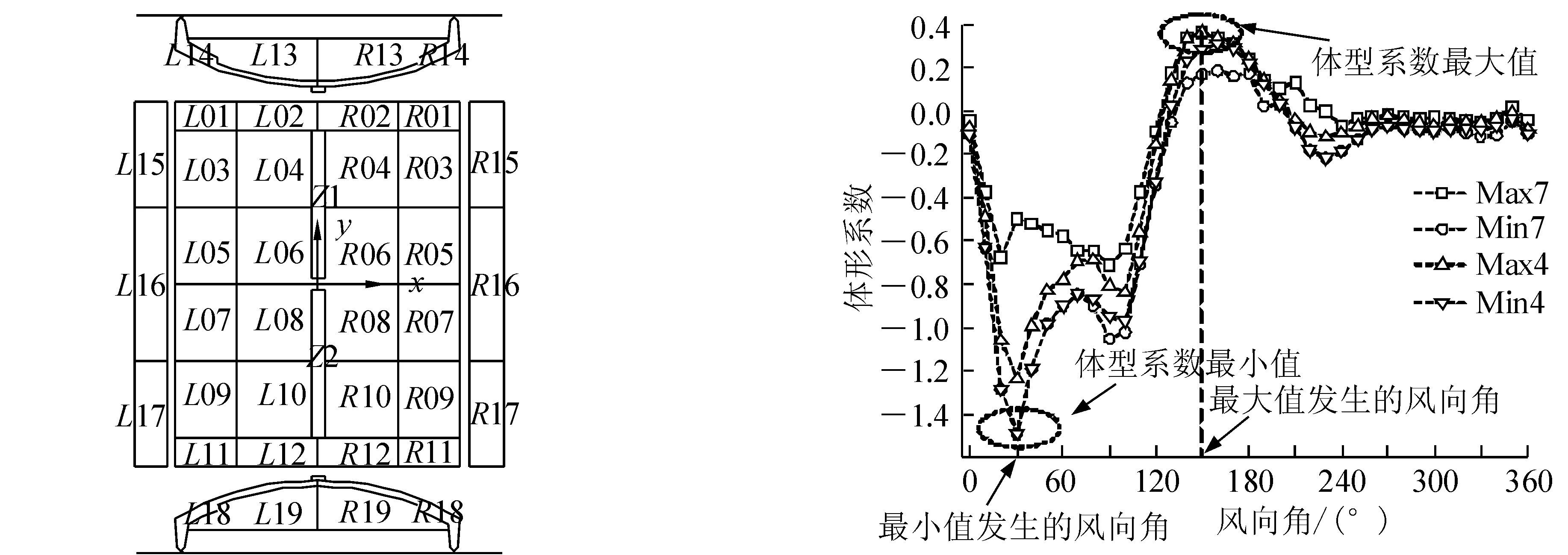
图4 分块示意图 图5 分块体型系数
2.3 整体力系数
对于大跨度空间结构,竖向荷载是主要的风致荷载,因此往往通过竖向荷载的大小来判断其风荷载的影响程度,通过对非结构化网格虚面风荷载积分得到的最大竖向力系数。定义最大竖向力系数为
(2)
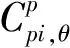
图6给出了结构整体竖向力系数,通过对比不同干扰工况下的力系数,可以看到,当结构在C2和C4工况下280°风向角下时,其竖向力系数最小,最强风荷载发生在C1和C3工况下。
2.4 节点力时程
在进行结构风致振动分析时,往往需要将测得的风荷载分配至结构不同位置的节点,采用非结构化网格技术,能够使得到的节点风荷载更准确,这主要得益于经过网格划分和插值后的风荷载分布更细,而且可以根据不同精度要求划分网格,本例采用2 m的网格长度。
该项目的结构动力分析模型共包含9 942个节点,每个节点的风荷载均可由该节点附近一定区域范围内的虚面风荷载计算得到。按照结构坐标系统,风压荷载转换为x、y、z3个方向的力,以此作为输入,可以通过时域方法(力时程直接输入)或者频域方法(将力转化为结构力谱输入)计算结构的风致抖振响应。
图7为结构顶部某节点在来流垂直于结构长轴时的典型力时程,其中横坐标t为时间,纵坐标F代表风荷载,x方向为结构短轴方向,y为结构长轴方向,z为竖向(见图 4),可以看出该节点在该工况下主要承受竖向风荷载作用。
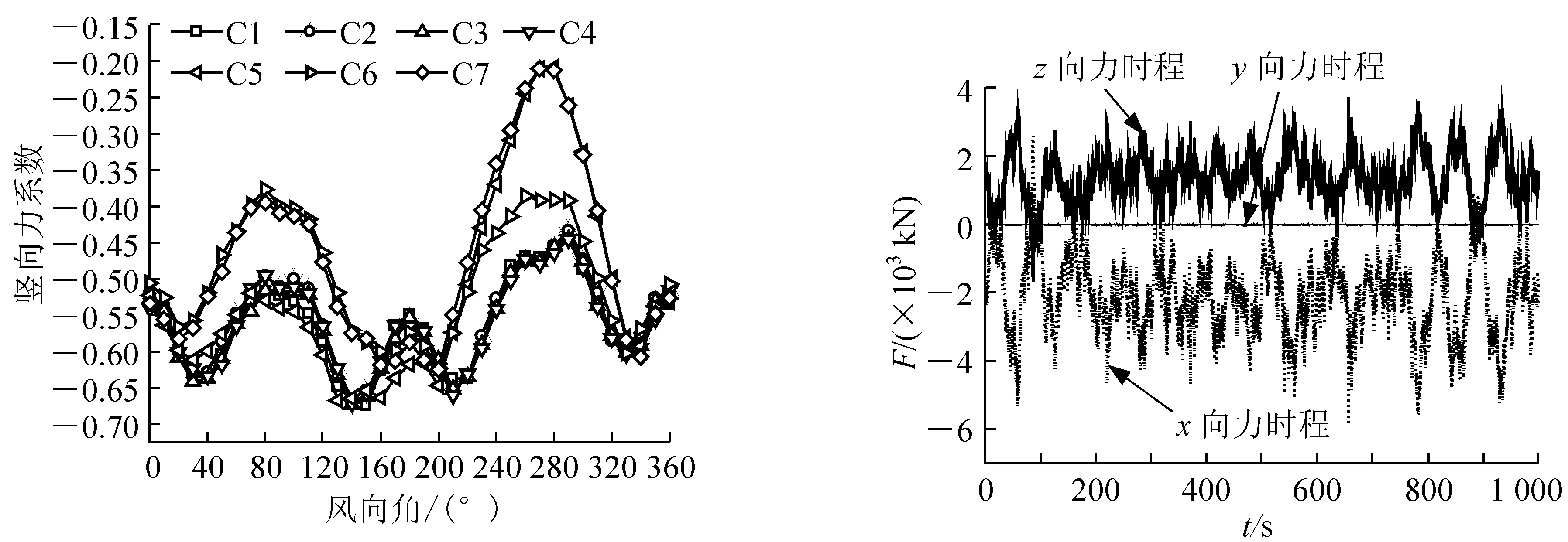
图6 结构整体力系数 图7 结构节点的力时程
3 结论
非结构化网格风荷载分配及处理的主要思想就是把有限元方法应用到结构风荷载分配及处理上来,这种方法最大的优点是通用性强、可控性强、处理结果准确。采用这种技术几乎可以处理刚性模型测压试验的任意风荷载,为准确合理使用刚性模型测压数据提供了保证,该方法目前在国内外仍未见报道。该方法的缺点是计算工作量与网格划分的密度有关,当对超大跨度结构进行网格划分时,其单元长度会受到限制,但是能够很好的满足目前结构抗风设计需要的精度。
参 考 文 献
[1]马文勇, 刘庆宽, 尉耀元.具有凹面外形的大跨度屋盖结构风荷载分布及风洞试验研究[J].振动与冲击,2012,31(22):34-38.
[2]马文勇, 刘庆宽, 肖彬.典型拱形壳体风荷载分布规律[J].土木建筑与环境工程, 2011,33(5):63-68.
[3]陆方夏,赵林,郭增伟,等.类矩形双肢钝体涡致振动和气动抑振机理[J].石家庄铁道大学学报:自然科学版,2010,23(4):10-14.
[4]谢壮宁,顾明,倪振华.复杂测压管路系统动态特性的通用分析程序[J].同济大学学报2003,31(6):702-708.
[5]樊友川,顾明,全涌.常开洞工业厂房风致内压试验研究[J].空气动力学学报,2011,29(5):585-591.

