梁格法在双曲拱桥承载能力评估中的应用

王灿辉 周彦庆 崔宏章

湖南城市学院土木工程学院（413000）

梁格法在双曲拱桥承载能力评估中的应用

王灿辉 周彦庆 崔宏章

湖南城市学院土木工程学院（413000）

这里以某双曲拱桥的承载力评估为例，分别采用桥梁博士及Midas civil建立了双曲拱桥模型，对该桥的承载能力进行了评估分析，同时在现场进行了荷载试验以对模拟结果进行验证。结果表明，有限元中的梁格法是双曲拱桥结构空间分析的一种有效方法，分析结果更接近实际情况；以梁格法理论分析和动静力荷载试验相结合的方法能较为全面地评定双曲拱桥的承载能力，可为同类桥梁计算分析及承载能力评定提供参考。

梁格法；双曲拱；模型；承载能力评估

双曲拱桥是20世纪60年代，由我国江苏省无锡县建桥工人首创的一种桥型。它由拱肋、拱波、拱板和横向联系等几部分组成，充分发挥了预制装配的优点，可以不要拱架施工。主拱圈以“化整为零”的方法按先后顺序进行施工，再以“集零为整“的方式组合成承重结构。该桥型节省木料，施工进度快，而所耗用的工料又不多,符合我国当时的国情[1]。在20世纪60、70年代,我国各地都修建了大量的双曲拱桥。但该桥型结构的整体性较差，在地震荷载的作用下容易破坏，并且在长期活载作用下拱肋与拱波结合处容易开裂，这些缺陷经过多年使用已暴露无遗。同时由于超载现象严重，使全国各地现存的双曲拱桥都有不同程度的破损，影响行车安全。由于已建双曲拱桥众多，把全部危桥拆除重建既不符合国情也不现实。为了保证其安全运营，需对其进行检测、评估。正确评价其承载能力，可以为维修、加固提供科学依据。理论研究表明，传统的拱桥计算方法,由于不考虑拱上建筑及其空间受力特点，难以准确反映其实际承载能力。桥梁博士和Midas civil是桥梁分析中常用的软件，但Midas civil以其建模速度快而且较为符合实际，还可以考虑结构的空间效应，已成为桥梁工程界广泛应用的有限元通用软件。这里采用Midas civil中的梁格法建立双曲拱的空间模型对桥梁的承载能力进行分析，并采用桥梁博士进行了对比分析。

1 双曲拱结构的分析方法

1.1 经典力学方法

传统双曲拱桥的内力计算方法为经典力学法，基本思想为:引入横向分配系数，计算出每根拱肋的横向分配系数，将荷载分到每根拱肋上，进行内力、强度及稳定性计算。这种计算方法较为繁琐，由于引入了大量假设，使得计算结果与实际结构也存在一定差别。

1.2 有限元方法

有限元法分析桥梁结构内力时，有多种离散模型，常用的有空间梁单元法、板壳元法、三维实体元法及梁格法。其中梁单元法能直接计算出界面的内力及变形，但不能得到内力的横向分布；板壳元法适合模拟结构尺寸与板相近的构件，模拟梁式构件误差较大；三维实体元法的优点是计算模型与实际模型最接近，不需计算截面参数，缺点是输出的是构件截面的节点应力,不能直接用于强度计算，当模型复杂时，计算费用高，数据处理繁琐，对于大型空间结构,如果单元模型过多,往往计算时间过长,占用大量资源；梁格法是分析桥梁上部结构较为实用的一种方法,它的特点是概念清晰,易于理解和使用[2]。

2 梁格法的原理

梁格法是有限元方法中的一种，是借助计算机分析桥梁上部结构的一种有效、实用的方法。它易于理解和使用，在桥梁结构设计中得到了广泛的应用，适用于板式、梁板式、箱梁上部结构及其他各种组合体系桥梁。

梁格法的主要思路是将上部结构用一个等效梁格来模拟。将分散在板式或箱梁的每一区段内的抗弯刚度和抗扭刚度集中于邻近的等效梁格内，实际结构的纵向刚度集中于纵向梁格构件内，而横向刚度则集中于横向梁格构件内。从理论上讲，梁格必须满足以下等效原则:当原型实际结构和对应的等效梁格承受相同荷载时,两者的挠曲应是恒等的，而且在任一梁格内的弯矩、剪力和扭矩应等于该梁格所代表的实际结构部分的内力。由于实际结构和梁格体系有着不同的结构特性，上述“等效”的理想状况是难以达到的，模拟只能是近似的。这种特性表现在以下方面:1）梁格法中任意梁内的弯矩严格与其曲率成正比，而原结构如板结构中，任一方向上的弯矩和该方向及正交方向上的曲率有关。对钢筋混凝土或预应力混凝土构件而言,一般按纵向、横向双向配筋，同时混凝土泊松比较小，所以用梁格法导出的纵向弯矩和横向弯矩对结构设计是足够准确的。2）实际板结构中，任一单元的平衡要求扭矩在正交方向上是相等的，而且扭率在正交方向上也是相同的。在等效梁格中由于两类结构特性不同，无法使扭矩、扭率在正交方向的节点上各自相等，然而梁格网格相当细密时，梁格随着挠曲而成一曲面，在正交方向上可近似相等[3]。

3 工程概况

株洲醴陵县某大桥是醴陵县某水库上的一座桥梁，全长93 m，净跨径74 m，桥面宽5.5 m（0.25 m+5.0 m+0.25 m），设计荷载等级为汽-15。上部结构为钢筋混凝土单跨结构，下部结构为片石混凝土重力式桥台。该桥因年代久远，腹拱多处横向裂缝，并渗水泛碱，主拱圈及腹拱出现局部空洞。考虑其多种病害并存，须对其进一步进行荷载试验，以推断其在荷载作用下的工作状态和承载能力。该双曲拱桥结构如图1所示。其Midas有限元模型如图2所示。

图1 双曲拱桥结构简图（单位:m）

图2 双曲拱桥Midas有限元模型

4 荷载试验

为了判断双曲拱桥实际受力性能，通过荷载试验对双曲拱桥做一次技术评估，根据现场的情况选择第一孔作为试验孔，选取该孔的拱顶截面以及拱脚截面作为荷载试验的主要测试截面。根据桥梁博士及Midas civil有限元计算结果，拟定以下静载试验项目:

工况Ⅰ:拱顶截面最大正弯矩。拱顶截面弯矩影响线及加载车布置见图3～5。

图3 桥梁博士拱顶截面弯矩影响线

图4 Midas civil拱顶截面弯矩影响线

图5 工况Ⅰ加载辆布置图（单位:m）

工况Ⅱ:0#台拱脚截面最大负弯矩。拱脚截面弯矩影响线及加载车布置见图6～8。

图6 桥梁博士0#台拱脚截面弯矩影响线

图7 Midas civil 0#台拱脚截面弯矩影响线

图8 工况Ⅱ加载辆布置图（单位：m）

5 试验结果分析

5.1 挠度测试结果分析

在试验过程中，对试验跨的支点截面和跨中截面进行了挠度观测。挠度测试值与桥梁博士及Midas civil理论值对比见表1。

表1 挠度测试值与有限元理论值对比（mm）

由表1可知，在所有工况中，双曲拱桥挠度实测值均小于理论值，校验系数小于1.0，说明双曲拱桥处于弹性工作状态，刚度满足要求；从数据对比看，Midas civil挠度理论值较桥梁博士的挠度理论值更接近实测值。在工况I中，Midas civil挠度校验系数相对桥梁博士挠度校验系数提高了24.04%。在工况II中，Midas civil挠度校验系数相对桥梁博士挠度校验系数提高了21.01%。

5.2 应变测试结果分析

试验选取试验跨各拱肋的拱顶截面和拱脚截面作为应变测试截面。应变测试结果对比见表2。注:表中正数表示测点受压，负数表示测点受拉。

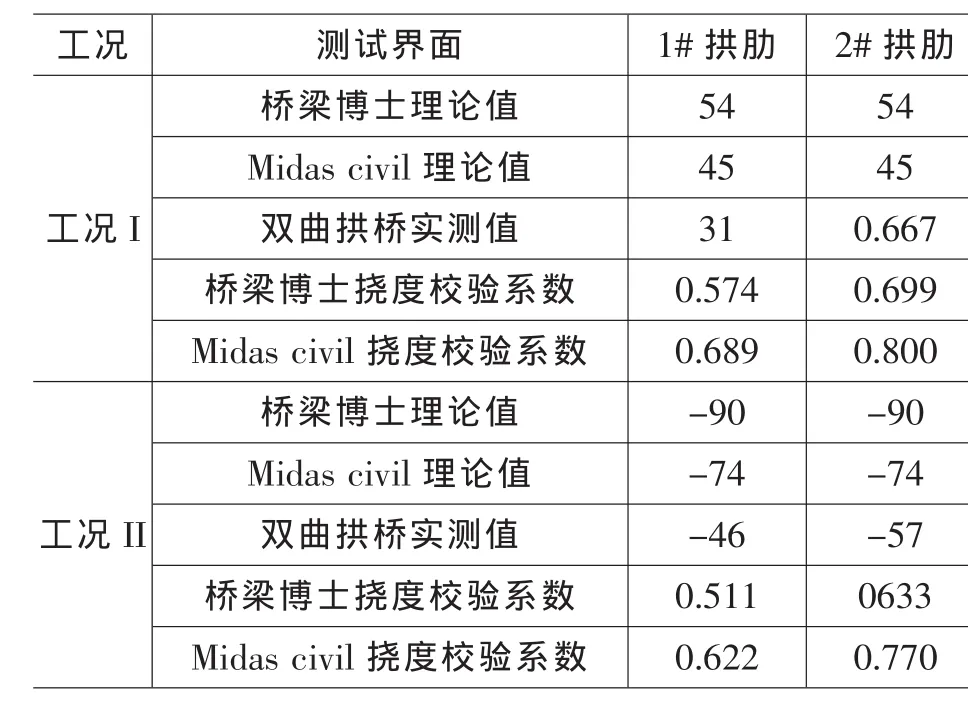
表2 应变测试值与有限元理论值对比（με）

由表2可知，在所有工况中，双曲拱桥应变实测值均小于理论值，校验系数小于1.0，说明双曲拱桥处于弹性工作状态，强度满足要求；同时从数据对比看，Midas civil应变理论值较桥梁博士的应变理论值更接近实测值。在工况I中，Midas civil挠度校验系数相对桥梁博士挠度校验系数提高了16.97%。在工况II中，Midas civil挠度校验系数相对桥梁博士挠度校验系数提高了21.68%。

6 结语

经与现场荷载试验对比分析，认为采用Midas civil中的梁格法建立双曲拱的空间模型对桥梁的承载能力进行分析是可行的，且该模型能更准确地模拟出双曲拱桥实际受力状况。

[1]黄侨,葛占利,林阳子.梁格法在双曲拱桥承载能力评估中的应用[J].中外公路,2007(12):89～93.

[2]杨勇,刘能文,金晶,李儒.某双曲拱桥的动静力测试及承载能力评估[J].特种结构,2012(10):75～80.

[3]戴公连,李建德.桥梁结构空间分析设计方法与应用[M].北京:人民交通出版社,2001:15～16.

湖南省教育厅科研基金资助项目（10C506）