资本资产定价模型的扩展及其在保险中的应用

张鸿雁，李丽玲

(中南大学 数学与统计学院，长沙 410083)

一、 引言

随着我国资本市场和保险市场的开放和完善，越来越多的保险公司和保险产品开始出现。如何制定一个合理、公平的费率，一直是保险公司和政府相关部门关注的重点，也是很多保险工作者及投保人所关心的问题。很多学者也在理论和应用方面做了不少研究，并尝试将资本资产定价模型应用到保险的费率制定当中。1964年，夏普[1](Sharpe)首先提出了CAPM模型(资本资产定价模型)。随后在1965年、1966年，林特纳[2](Lintner)、莫辛[3](Mossin)也都分别提出了各自的CAPM模型。此模型主要用于研究证券市场中均衡价格的形成，以此来寻找证券市场中被错误定价的证券。1970年，Brennan[4]放宽了对无税收的假设, 考虑了税率对证券风险报酬的影响。赵正堂[5]则研究了金融型保险产品的定价模型，包括CAPM模型、套利定价模型(APT)、期权定价模型(OPM)和评估模型，并比较和评述了各个定价模型。他认为，OPM和APT可以通过结合金融市场上的风险附加使CAPM得到一定改进。方俊芝、唐敏[6]研究了资本资产定价模型在保险产品定价中的应用，其中包括一般保险产品和巨灾保险产品。钱敏[7]研究了资本资产定价模型和期权定价模型用于保险费率厘定的情况。他认为，资本资产定价模型在考虑了保险基金运用的基础上，可以用来厘定风险附加费率。景乃权[8]对CAPM的应用条件作了分析，对它的应用作了评述，并认为它具有简单明确和实用性特点。韩俊霞[9]考虑了保险公司存在违约风险时的公平保费的定价，并通过修改资本资产定价模型的一些条件，得到了更客观的保费厘定模型。本文是在前人研究的基础上，特别是受到韩俊霞、高俊山[9]等人研究的启发，对模型的应用条件进行了修改或增加，并探讨了模型扩展后在保险费率制定中的应用问题：一是考虑了存在税收情况的公平保费，并讨论了税收分别为固定值和变量的情形；二是考虑公司若采取再保险策略时的公平保费；三是考虑了承保费用为保费的函数的情形。其中，公式(1)～(37)是文献[9]中的研究成果,(38)～(58)是本文经研究推导所得。

二 、相关问题描述

假定保险公司有资金(或者叫盈余)为K,已发行的总保单保费价值为P，到期时需支付的总索赔为X，这是一个带有均值的随机变量。保险公司把它的所有资金(包括它的盈余和收取的保费)都投于金融市场，其中回报率为ri，若把保险公司的净资产和总收益的和记为V，则有(1)式成立：

V=(K+P)(1+ri)-X

(1)

当保险公司的净资产为负值时，它就会破产。因为保险公司对于它的投保人的权益支付是有限的，所以在保险公司破产的情况下，它的实际利益为Π=-K;如果保险公司具有偿付能力，它的实际权益为

Π=V-K

(2)

换言之，我们有：

Π=V-K+Max(0,-V)

(3)

或者

Π=V-K+Z

(4)

其中

Z=Max(0,-V)

(5)

Z叫做公司的破产期权值。

那么，我们的问题是如何确定公平保费P，使得这样的保费对于保险公司和投保人都是公平的、合理的，并且有利于保险事业的顺利发展。因为保费过高，投保人投保的意愿降低，公司难以收取到所需的保费。而保费过低，保险公司因无法得到足够的保费，将无法得到顺利发展，并会导致破产，同时由于保费过低导致投保人投入过量的资金而得不到回报，使保险市场无法顺利发展。

三、保费定价模型的建立及求解

现在我们将通过建立合适的模型来解答以上的问题。

令

π=Π/K

(6)

π为收益率。那么,可以得到：

(7)

其中

(8)

ru是承保收益率。

(9)

且有:

E(ri)=rf+βi[E(rm)-rf]

(10)

其中，rf为无风险利率，rm为市场m的回报率，E(rm)是市场m的预期市场回报率。

然而，由Sharpe[1]、Lintner[2]及Mossin[3]提出的资本资产定价模型可知：

E(π)=rf+β[E(rm)-rf]

(11)

其中：β是常数，称为资产β(asset beta)。β系数反映了资产的回报率对市场变动的敏感程度，βi为资产i的风险系数。

β=Cov(rm,π)/Var(rm)

(12)

βi=Cov(rm,ri)/Var(rm)

(13)

此外，由收益率的定义可知：

(14)

其中βu是承保的β系数，

(15)

βu=-Cov(X,rm)/[PVar(rm)]

(16)

把(15)式代入(11)，再把(11)和(10)代入(9)式，我们可以得到：

(17)

整理上面这个方程，可得：

E(ru)= -rf+βu(E(rm)-rf)-

(18)

或者

E(ru)=-rf+βu(E(rm)-rf)-VP

(19)

其中:

(20)

我们把VP叫做每单位保费的市场期权值，E(ru)为承保收益率的期望。

如果保险公司没有违约风险，则

Z=0，βz/p=0

(21)

这样就可得到：

E(ru)=-rf+βu(E(rm)-rf)

(22)

由(8)式、(15)式和(18)式可得：

βz(E(rm)-rf)])/(1+rf)

(23)

或者

(24)

其中：

λ=(E(rm)-rf)/Var(rm)

(25)

λ叫做市场风险保费。

TVP=E(Z)-βz(E(rm)-rf)

(26)

TVP为期权的市场总值。

同样的，当保险公司没有违约风险时，

Z=βz=0

(27)

由此可得

(28)

式(28)即为保险公司不存在违约风险时的公平保费[9]。

当经济环境较好时，公司的破产概率会变低，由此得到βz/p≤0、Z≥0。因此，我们有VP≥0和TVP≥0，并有(29)式和(30)式成立

E(ru)≤-rf+βu(E(rm)-rf)

(29)

(30)

当且仅当Z=0时，得到

E(ru)=-rf+βu(E(rm)-rf)

(31)

且

(32)

也就是说，因为保险公司存在破产风险，所以会降低承保利润率和保费。

四 、保费定价模型的扩展

(一)考虑交易费用和投资比例的保费定价模型

在上面公平保费的推导过程中，我们假定了无交易费用，而且在一开始保险公司就把所获得的保费全都可以投入到市场中了。

现在，我们假定公司总的交易费用为C，且只把收取的保费按比例δ投入市场中，此时公司的总资产值为：

V= (K+δ(P-C))(1+ri)+

(1-δ)(P-C)-X

(33)

其中：

(34)

ru依然定义为承保利润率。

注意到此时

(35)

重复前面的推导过程，我们可以得到：

E(ru)= -δ(1-c)rf+βu(E(rm)-rf)-

(36)

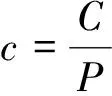
βz(E(rm)-rf)])/(1+δrf)

(37)

这样得到的公式(37)就是在同时考虑了投资比例和承保费用的情况下的公平保费。

从(36)式、(37)式可以看出，当保险公司投入越低比例的保费到市场中，它就需要更高的补偿；保险公司的交易费用C越多，保费也越高。

(二)考虑承保费用不是常数和再保险的保费定价模型

一般情况下，承保费用支出并不会是一个常数，而是一个与保费收入有关的一个函数。在此部分，假设承保费用不是一个固定的值。承保费用为C(P)=f(P)，即C为关于P的一个函数，f(P)与保费P有着正相关关系。

在现实生活中，一些财产保险公司还会参与再保险，运用再保险策略分担自身的保险风险。为简单起见，这里假设原公司采取成比例再保险策略，设再保险费用为P1，其中

P1=δ1P(0≤δ1≤1)

(38)

其中，δ1为再保险比例。

此时可得

V= [K+δ(P-f(P)-δ1P)](1+ri)+

(1-δ)(P-f(P)-δ1P)-X

(39)

δ的含义仍为投入市场中的保费与收取的保费之比。此时的承保利润率为

(40)

同样的，由(6)式可得：

(41)

对(41)式两边取平均值，可得：

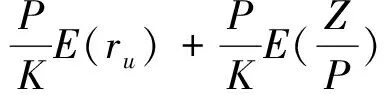
(42)

E(π)为此时的实际收益的期望。而此时的β系数为：

(43)

把(43)代入(11)式，再把(11)式和(10)式代入(42)式，化简可得

βz/p(E(rm)-rf)]

(44)

若f(P)没有具体的形式，由(20)式可知此时保费的收取必须满足：

λCov(X,rm)-[E(Z)-βz(E(rm)-

rf)]}/{1-δ1+δrf-δ1δrf}

(45)

因为f(P)与保费P正相关，则可假设

f(P)=k1P+b

(46)

即：可以认为f(P)与P为线性关系，且为P的一次函数。其中k1为承保费用与保费之间的相关系数，b为某些固定的费用。这个假设是合理的。一般情况下，有些保费是固定的，其他的比如手续费、员工工资都可以被认为是与P成正比的，所以假定f(P)与P为一次函数关系是可行的。此时:

βz/p(E(rm)-rf)]

(47)

注意到此时

(48)

类似的，可以求得此时的保费

[E(Z)-βz(E(rm)-rf)}/{1-k1-

δ1+δrf-δ1δrf-k1δrf}

(49)

由(47)式可以看出，δ1越小，即再保险比例越小, 所需保费也越少；k1越小，即承保费用与保费的正相关系数越小，需收取的保费也越少。如果提高办事效率，相应所需员工越少，并且在收取保费时相应的承保费用越少，所需保费更少。这是符合实际情况的。

(三)考虑税收时的保费定价模型

(1)税收T为固定值时的定价模型。在考虑公司有交易成本的情况下，还可以考虑在公司要纳税的情况下来调整保费的公平定价。假定法定的税率为T，θ1T代表公司投资收入的平均税率，其中0≤θ1≤1。现在我们令θ2T为法定的承保利润税率。那么，我们可以重新定义在任何给定的承保利润率E(ru)情况下股东的期望回报。即

(50)

E(π)为股东的期望回报。最后可以得到：

βz/p(E(rm)-rf)]

(51)

以及

P=C+(Kθ1rfT)/[(1-θ2T)+δrf(1-θ1T)]+

(52)

式(52)为同时考虑存在承保费用和投资比例、同时公司存在税赋情形下的公平保费。这时的保费与税率T有着固定的关系，且由(52)式可知，税率T越小，保费P也越小。这与实际生活中的金融市场是相符的，税收少，所需保费也理所当然减少。

(2)税收为变量时的定价模型。在现实生活中，一般情况下，保险公司的股本在成立时已经固定不变，所以保险公司投入到金融市场中的资金主要依赖于收取的保费，从而公司的投资收入和承保利润都会受到保费的影响。因此，保险公司的税收要依赖于所收保费的多少。

设此时税收T=T(P),即T为一个关于P的函数，这样的考虑更加符合实际情况。在此情形下，我们重新考虑承保利润率和公平保费的定价。为简单起见，假设此时承保费用C=C(P),只把获得的保费按照一定的比例投资到市场中，投资比例为δ。此时不再考虑再保险。类似的，可求得此时的利润率为：

(53)

其中：

(54)

c(P)为承保费用与保费相关时每单位保费的平均支出。假设税收与保费成正比关系，即：

T(P)=k2P(k2>0)

(55)

其中，k2为税收与保费的比例系数。特别的，当无保费收入时，税收为0。此时承保利润率期望为：

(56)

其中：

(57)

此为在考虑了交易费用后的承保利润率。

求得此时的公平保费P满足：

[E(Z)-βz(E(rm)-rf)]

(58)

考虑交费费用为C(P)(即C为保费P的函数)，税率T为T(P)=k2P(即T为保费的正比例函数)时，此时得到的保费即为(58)式。上述分析表明,在综合考虑了众多因素后，保费P的表达式比较复杂，此时考虑的交易费用与保费的关系不一定是一次函数关系，所以得到的是(57)式。显然，税率T越小，保费将越少。

(四)基本结论

定理 (1)在考虑保险公司的破产风险时，保费的定价为：

其中，λ=(E(rm)-rf)/Var(rm)为市场风险保费；TVP=E(Z)-βz(E(rm)-rf)为期权的市场总值。

此时的承保收益率的期望为：

E(ru)=-rf+βu(E(rm)-rf)-VP

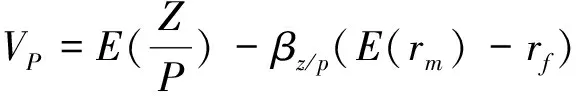
(2)考虑交易费用和投资比例时，保险的公平保费价格以及平均承保收益率为：

[E(Z)-βz(E(rm)-rf)])/(1+δrf)

βu(E(rm)-rf)-Vp

其中，λCov(X,rm)是保险公司的承保风险保费。

(3)考虑承保费用不是常数和再保险的公平保费为：

设再保险费用为P1，则

P1=δ1P(0≤δ1≤1)

其中，δ1为再保险比例。

①承保费用为C(P)=f(P)时，若f(P)没有具体的形式，由(19)式得到此时保费的收取必须满足：

[E(Z)-βz(E(rm)-rf)]}/{1-δ1+δrf-

δ1δrf}

②f(P)=k1P+b( 其中k1为承保费用与保费之间的相关系数，b为某些固定的费用)时，可得

[E(Z)-βz(E(rm)-rf)]}/{1-δ1+δrf-

δ1δrf}

(4)考虑税收时的保费价格

①税收T为固定值时：

P=C+(Kθ1rfT)/[(1-θ2T)+δrf(1-θ1T)]+

②税收为变量时，设此时税收T=T(P)，此时的公平保费P满足：

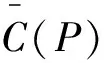
五、结论

由传统的资本资产定价模型得到的保费，是偏高的，因为它没有考虑违约风险。本文则证明了在考虑了保险公司的破产风险后，保费应会更低。在考虑了破产风险之后，保险人所要求的收益率也会变低。再保险比例越小，所需保费也越少。如果提高办事效率，相应所需员工越少，并且在收取保费时相应的承保费用越少，则所需保费更少。此外，保费的收取与税率有关。

鉴于相关研究数据的取得较为困难，所以本文未能进行更为深入的实证分析，这也是本文研究的一大遗憾，也期待在后续研究中进行。

参考文献：

[1]William F. Sharpe. Capital Asset Prices: A theory of market equilibrium under condition of risk [J].TheJournalofFinance,1964,(3):425-442.

[2]John Lintner. Security prices, risk, and maximal gains from diversification [J].TheJournalofFinance,1965,(4): 587-615.

[3]Jan Mossin. Equilibrium in a Capital Asset Market [J].Econometrica,1966, 4:768-783.

[4]M. J. Brenanan. Taxes, market valuation and corporate financial policy [J].NationalTaxJournal,1970, (2):321-352.

[5]赵正堂. 金融型保险产品定价模型研究[J].厦门大学学报：哲学社会科学版,2008,(4):42-51.

[6]方俊芝,唐敏.资本资产定价模型在保险产品定价中的应用[J].生产力研究,2010,(5):86-90.

[7]钱敏.基于资产定价理论的保险费率研究[J].重庆大学学报：社会科学版,2010,16(3):46-51.

[8]景乃权.资本资产定价模型及其评述[J].经济学家,2000,(04):116-120.

[9]韩俊霞,高俊山.资本资产定价模型在保险中的应用[J].知识丛林, 2005，(11):130-131.