一种确定坝肩防渗帷幕长度的方法研究

张德全，赵小平

（1.大同市御河水利管理处，山西 大同 037006；2.山西省水利水电工程建设监理有限公司，山西 太原 030002）

一种确定坝肩防渗帷幕长度的方法研究

张德全1，赵小平2

（1.大同市御河水利管理处，山西 大同 037006；2.山西省水利水电工程建设监理有限公司，山西 太原 030002）

安全与经济始终是工程设计中需要认真处理的一对矛盾问题，本文基于左右坝肩单位面积的最大渗流量（最大流速）与坝基单位面积的最大渗流量（最大流速）相等的原则，推导了坝肩防渗帷幕长度的公式。以一个实际工程为例，分别用公式法以及有限元计算法，计算了坝肩防渗帷幕的最优长度。计算结果表明：在满足渗透坡降、渗流量、渗流速度、水头高程的前提下，二者的计算结果基本一致。验证了本方法的有效性，对工程计算与设计具有一定的指导意义。

防渗帷幕；复合防渗体；渗流量；渗透稳定性

1 概述

大坝坝肩的防渗处理始终是大坝设计中的关键问题，出于安全的原因，总想把坝肩防渗墙尽可能延长；出于经济的原因，则总想把坝肩防渗墙尽量缩短。安全与经济始终是工程设计中不可回避的一对矛盾。目前，确定坝肩防渗帷幕长度的方法可分为两类：一类是传统的绕渗水力计算方法［1-2］，另一类有限元渗流计算方法［3-5］。第一类方法，虽然是传统的计算方法，但计算繁琐，简化条件多，影响计算的精度；第二类方法，以有限元为基础，建模计算绕渗流量等参数，计算精度高，但还不普遍。

本文给出了一种新的计算方法，并以一个工程为例，分别以公式计算、Seep-3D渗流计算进行了对比，由此确定了坝肩防渗帷幕的防渗长度。

2 防渗帷幕长度计算方法研究

几乎所有的大坝在修建时都要进行坝基及坝肩的防渗处理，不管是用灌浆还是用防渗墙的方法。防渗处理后的大坝仍然会存在坝基及坝肩的渗漏，只不过是防渗处理后的坝基已满足渗透稳定性的标准、坝肩已满足设计渗流量的要求。本文建议的防渗帷幕长计算的公式基于以下原则：即，经过防渗处理的坝肩及坝基，其左右坝肩单位面积的最大渗流量（最大流速）与坝基单位面积的最大渗流量（最大流速）相等。

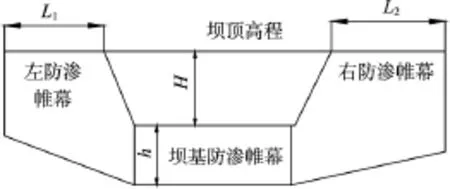
图1 大坝示意图

从图1可以发现，坝肩单位面积的最大渗流量（最大流速）发生的部位在防渗帷幕最远端的最底部，坝基单位面积的最大渗流量（最大流速）发生的部位在防渗帷幕的最底部。

由此可建立以下的公式（1）：

式中：v1、v2、v3分别为右坝肩、左坝肩、坝基的最大渗流速度。

式中：k1(i1)、k2(i2)、k3(i3)分别为右坝肩、左坝肩、坝基的渗透系数（水力坡降）；L1、L2分别为右坝肩、左坝肩防渗帷幕长度；H为最大蓄水深度（从建基面算起）；h坝基帷幕深度。

将式（2）、式（3）、式（4）代入式（1），得：

化简得：

3 算例

黄河大河家水库工程位于甘肃积石山县境内，坝型为土工膜心墙砂砾石坝，在坝轴线上布置有防渗复合土工膜，复合土工膜向下延伸与坝基底部的防渗墙相连。左右两岸为挡水坝段，中部为泄洪闸段。坝高25.5m，坝顶宽6.0m，坝基底部最大宽度111.17m，上游坝坡坡度1∶2.5，下游坝坡坡度1∶1.6，水库正常蓄水高程1 783 m，下游水位高程1 771m，坝前最高蓄水深度23.5m，坝基防渗墙深度20m，至相对隔水层。由于两岸坡度较缓，分化岩层延伸距离较远，若全部进行防渗处理，势必增加很大的工程量及投资，因此确定一个最优的两岸防渗长度，就成为设计面临的重要课题。

经过反复研究，兼顾防渗效果达到最佳而又经济投入最小的原则，决定基于左右坝肩单位面积的最大渗流量（最大流速）与坝基单位面积的最大渗流量（最大流速）相等的原则，确定坝肩防渗的长度。计算参数取：

h=20m，H=23.5m，k1=1.8×10-4cm/s，k2=3.6×10-4cm/s，k3=2.67×10-5cm/s

代入式（6）、式（7）得：

右岸防渗长度L1=72.8m，左岸防渗长度L2=145.6m。

4 复核计算

为了验算计算结果，仍以该工程为例，利用有限元渗流计算软件Seep-3D，进行了建模计算。

4.1 计算条件坐标系的选取：采用三维直角坐标系，原点取在工程坐标（0，1741，0）处，以平行坝轴线方向、且指向左岸为x轴的正方向，以垂直坝轴线的顺河流方向为z轴的正方向，以垂直坝轴线的垂直向上为y轴的正方向。

计算区域的选取：计算的上游边界取至坝轴线水平向上游的160m长度处，下游边界至坝轴线向下游的260 m长度处，底部边界至坝基以下58m（至高程1 684 m）处，左岸边界至左岸坝肩向外200m长度处，右岸边界至右岸堰肩向外200m长度处。

材料分布及计算参数：计算区域中共有8种不同的材料，在模型中分别用不同的颜色表示，8种分别为：帷幕灌浆，防渗墙，覆盖层Ⅰ，覆盖层Ⅱ，基岩，左右坝坝体，厂房坝段，复合防渗体。材料分区如图2所示。

所谓复合防渗体的定义是指为了建模方便，在计算过程中把混凝土面层、土工膜按渗透水量相等的原则等效处理为一种均质材料，称其为复合防渗体。

复合防渗体的渗透系数可按照以下方法计算得出。

图2 材料分区图

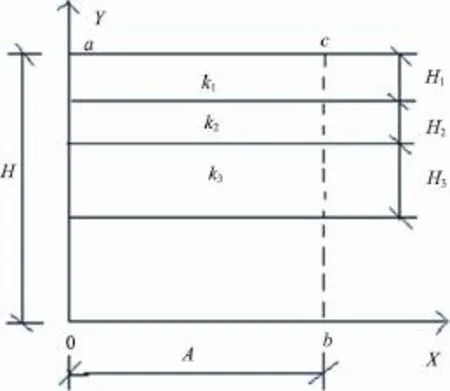
图3 复合防渗体渗透系数计算图

某层状地层如图3所示，土层厚度为H，总水力坡降为i，水流方向垂直于土层方向，水流流经各土层的水力坡降分别为i1，i2，i3……。土层的总渗流量q应与各层的渗流量q1，q2，q3……相等，即

式中A为渗流经过的截面积。

其次，总水头损失应等于各层水头损失的总和，

联解式（9）、式（10）两式得：

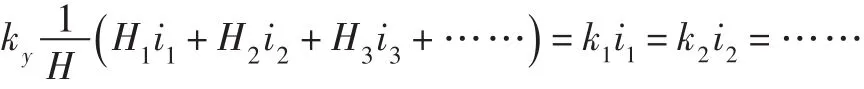
所以沿y方向的平均渗透系数ky为：

计算参数如表1所示。

计算边界及网格划分：计算区域的河道内为指定水头边界，其中坝上游水头高程1 783.1m、死水位高程1 782.06m，坝下游水头高程1 771.0m；模型底部边界为不透水边界；左右两岸边界为不透水边界。模型共划分节点数23万多个，单元数为21万多个，网格划分结果如图4所示。

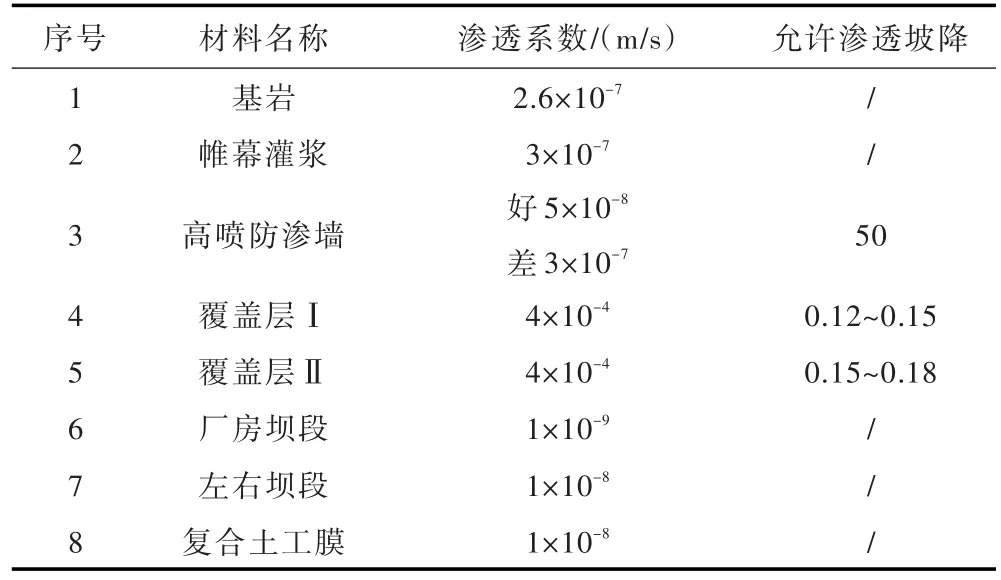
表1 渗流计算参数表

图4 网格划分图

4.2 结果分析

4.4.1 计算工况

工况1：右岸防渗帷幕长度50m，左岸防渗帷幕长度加倍，坝前正常蓄水位高程1 783.1m，下游正常蓄水位高程1 771m。

工况2：右岸防渗帷幕长度75m，左岸防渗帷幕长度加倍，坝前正常蓄水位高程1 783.1m，下游正常蓄水位高程1 771m。

工况3：右岸防渗帷幕长度150m，左岸防渗帷幕长度加倍，坝前正常蓄水位高程1 783.1m，下游正常蓄水位高程1 771m。

4.4.2 计算结果计算结果如表2—表5所示。

表2 渗透坡降计算结果

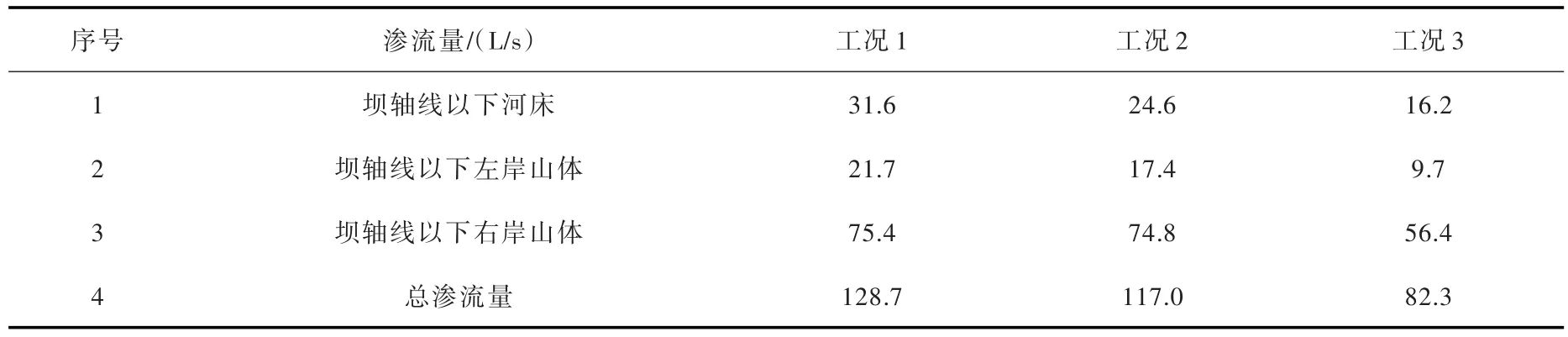
表3 渗流量计算结果

表4 渗流速度计算结果

表5 水头高程计算结果

4.4.3结果分析从表2分析可知，由工况1向工况3变化时，砂卵石层的渗透坡降呈逐渐减小趋势，工况1时的砂卵石层最大渗透坡降已超过了允许坡降值，工况2、工况3的砂卵石层最大渗透坡降均在允许值范围内，但工况3时不经济，因此工况2时最经济的选择。高喷防渗墙的最大渗透坡降均未超过允许坡降值，任一工况的最大渗透坡降均可满足设计要求。

图5 高程1 741.5m的坡降等值线图

图6 高程1 741.5m的流速等值线图

图7 高程1 741.5m的水头高程等值线图

从表3、表4分析可知，由工况1向工况3变化时，渗流量（渗流速度）均呈逐渐减小趋势。由于右岸防渗帷幕长度比左岸防渗帷幕长度短，因此右岸山体的渗流量要比左岸的大。三种工况下的渗流速度、渗流量均能满足坝坡渗透稳定性要求。

从表5分析可知，由工况1向工况3变化时，因渗径的延长，最大水头高程呈逐渐减小趋势；由于右岸防渗帷幕长度比左岸的短、右岸渗流量大，因此防渗墙右端处的最大水头高程较左端处的低。

综合以上分析，工况2是本项目的最优工况，最优工况时的坡降、流速、水头高程等值线图如图5—图7。

由此确定防渗帷幕长度为右岸段75m、左岸段150m。

5 结论

（1）基于大坝左右坝肩单位面积的最大渗流量（最大流速）与坝基单位面积的最大渗流量（最大流速）相等的原则，推导出了确定坝肩防渗帷幕长度的公式。

（2）以一工程实际为例，应用该公式计算出了左右岸防渗帷幕的长度；并通过有限元渗流计算软件，计算确定了左右岸防渗帷幕的最优长度，二者的结果基本一致，并由此最终确定了工程的帷幕长度，使得工程设计取得了安全与经济的最佳效果。

［1］毛昶熙.渗流计算分析与控制［M］.北京：水利电力出版社，1990.

［2］柴军瑞.大坝工程渗流力学［M］.西藏：西藏人民出版社，2001.

［3］王学武，党发宁，蒋力，等.深厚复杂覆盖层上高土石围堰三维渗透稳定性分析［J］.水利学报，2010，41（9）：1074-1079.

［4］梁国钱，郑敏生，孙伯永，等.土石坝渗流观测资料分析模型及防法［J］.水利学报，2003（2）：83-87.

［5］谢红强，何江达，张建海，等.紫坪铺水利工程右岸三维渗流场特性研究［J］.四川大学学报：工程科学版，2001，33（6）：10-13.

A m ethod to determ ine the length of im pervious cu r tain on dam abu tm en t

ZHANG De-quan1，ZHAO Xiao-ping2
（1.Datong Yuhe irrigationmanagementoffice，Datong 037006，China；2.Shanxiwater conservancy and hydropower engineering construction supervision lim ited company，Taiyuan 030002，China）

Security and cost are a contradictory problem，which always need to take care of in engineering design.Based on the principle that the maximum seepage flow per unit area（maximum velocity）through the left and right abutments equal to the maximum seepage flow per unit area（maximum velocity）of dam foundation，the length formula of impervious curtain on dam abutment was deduced.W ith a example of a real project，the optimal length of impervious curtain was confirmed by using the formula method and finite element method respectively.The calculation results were basically the same when the seepage gradient，seepage flow，seepage velocity and water elevation head met the requirements.The reasonable of this meth⁃od has been verified.It has a certain guiding significance for engineering calculation and design.

impervious curtain；composite impervious body；seepage flow；seepage stability

TV223.4

A

10.13244/j.cnki.jiwhr.2014.04.005

1672-3031（2014）04-0366-05

（责任编辑：李福田）

2014-10-21

国家自然科学基金面上项目（50879069，50679073）；水利部公益性行业科研专项（2007SHZ1—200701004）

张德全（1963-），男，山西人，高级工程师，主要从事水利工程施工方面的研究。E-mail：1374580142@qq.com