基于小波优化神经网络的故障定位算法研究*

臧川，江冰，薛心怡，殷杰

（1.河海大学物联网工程学院，江苏常州213022；2.江苏省输配电装备技术重点实验室，江苏常州213022；3.苏州市华东电网电气有限公司，江苏苏州215126）

在电力系统运行中，小电流接地系统单相接地故障发生的概率高达80%以上，远远高于相间短路、两相接地短路等故障发生率。不少经济发达地区的10 kV电网规划和改造都朝着以电缆供电为主、架空供电为辅的趋势发展。为了提高供电可靠性并减少电网故障带来的停电影响，供电系统都在积极实施配电运行自动化技术，通过实时监视及时发现隐患，避免事故的发生，并自动实现故障的定位、隔离及非故障线路的供电恢复，减少故障停电时间。因此，如何在10 kV配电网故障定位是一个值得研究和重视的课题[1-2]。

[3]提出了基于S注入法的选线定位原理，利用故障时暂时闲置的电压互感器注入交流信号电流在故障线路中跟踪寻找所注入信号的通路进行选线和定位，但是当发生高阻接地时，易受导线分布电容影响，且寻找故障点花费时间较长，有可能在此期间引发系统第二点接地，造成线路自动跳闸；参考文献[4]通过行波法测距，即通过分单端法和双端法测量故障点产生的行波在故障点及母线之间往返的时间或利用故障行波到达线路两端的时间差来计算故障距离，其主要优点是构成简单，容易实现，但行波信号的检测存在困难；参考文献[5]提出了基于区段零序电流的相对性定位方法，该方法根据区段零序电流特点构造了幅值判据和相位判据，需要在馈线上安装大量新型配电开关，投资增大，对通信要求较高，而且只能确定故障分支，不能确定故障点位置；参考文献[6]提出以故障馈线的非故障相暂态电流作为故障测距的基本依据，利用小波包对信号进行处理后寻找信号奇异点来确定故障区段，通过信号的相关性分析来确定故障点位置，这种定位简单，易于实现，但可靠性不强，并在实用性上还需进一步研究。

针对上述分析，本文在利用小波变换模极大值的奇异性检测对故障暂态信息量提取特征分量的基础上，将神经网络良好的非线性拟合能力和遗传算法的全局寻优能力相融合，实现故障特征分量与故障点位置之间的映射，从而实现故障点精确定位，即小波优化神经网络的故障定位。

1 单相接地故障电流分析

中性点不接地系统中，接地故障电流是通过电源变压器的假想接地中性点接地，给单相接地故障电流提供通路。如图1所示,假设线路2的A相发生单相接地故障，UA=0，则对于非故障线路1，A、B、C三相对地电容电流分别为：

图1 中性点不接地系统单相接地故障

非故障线路1的基波稳态零序电流为：

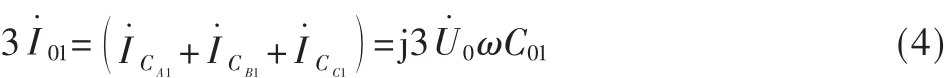
对于故障线路2，A、B、C三相对地电容电流分别为：

由上面公式可得故障线路2的零序电流为：

因此故障线路零序电流为所有非故障线路的零序电流之和，方向与非故障线路相反，为线路流向母线；流过故障点的电流是所有非故障相对地电容电流之和；并且，母线电压在故障时刻也会有一个变化量，因此以这两个变量作为特征量。

2 小波模极大值的信号奇异性检测

一个信号f(t)的卷积型小波变换：

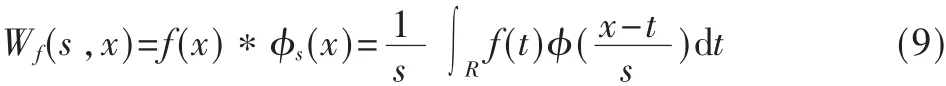
一个突变的信号在其突变点必然是奇异的。信号的奇异性用lipischitz α来描述，它的定义如下：

设0≤α≤1，如果存在常数K，使得在点t0的领域有下式成立：

则称函数f(t)在t0的奇异性指数是α。如果α=1，则函数f(t)在t0是可微的，称函数f(t)没有奇异性；如果α=0，则函数f(t)在t0间断。α越大，说明奇异函数f(t)越不奇异；α越小，说明奇异函数f(t)在t0点变化越尖锐[7]。函数的奇异性数值可用小波变换模极大值在不同尺度的数值计算出来。函数f(t)∈L2(R)与它的小波变换满足如下关系：

当s取为2j且W2jf(t0)是小波变换模极大值时，从上式可得：

可以得出lipischitz α为：

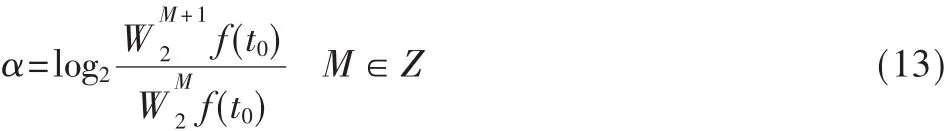
上式给出了具有突变性质的信号在何时发生突变以及变化剧烈程度的数学描述,即用小波变换模极大值表示。

3 优化神经网络的故障定位算法

3.1 优化神经网络的建模

BP(Back Propagation)网络是人工神经网络中应用最为广泛的一种模型，但它具有学习效率低、收敛速度慢、易陷入局部极小状态等缺点。因此，本文结合BP神经网络和遗传算法来构建适合于10 kV中性点不接地系统的单相接地故障定位模型。该模型分为3层：输入层、隐含层和输出层。输入层为故障信号小波变换的模极大值，输出层包含单一神经元，其值反映故障点位置，采用故障点与母线之间距离的归一化值来表示。优化神经网络的结构如图2所示。

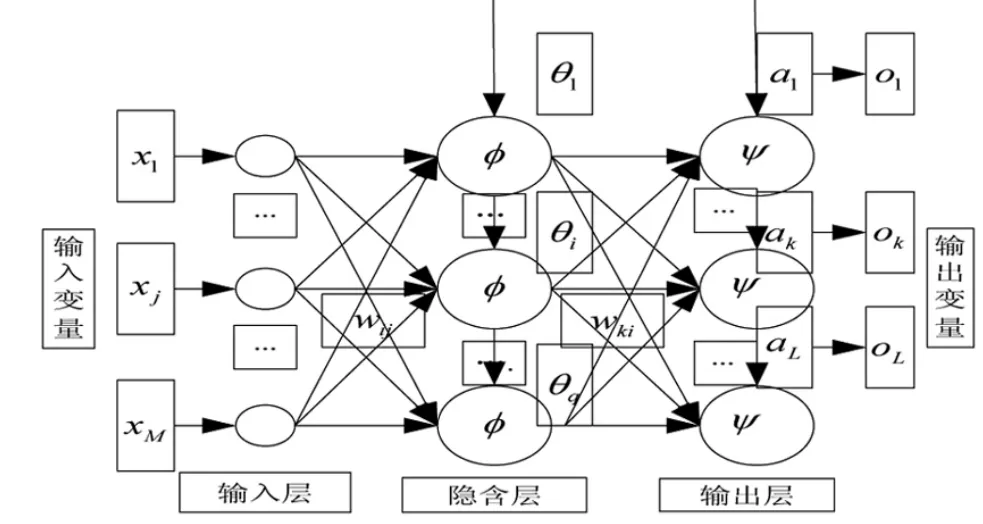
图2 优化神经网络的结构

图2中xj表示输入层第j个节点的输入，j=1，…，M；wij表示隐含层第i个节点到输入层第j个节点之间的权值；θi表示隐含层第i个节点的阈值；φ(x)表示隐含层的激励函数；wki表示输出层第k个节点到隐含层第i个节点之间的权值，i=1，…，q；αk表示输出层第k个节点的阈值，k=1，…，L；Ψ(x)表示输出层的激励函数；ok表示输出层第k点的输出[8]。

3.2 优化神经网络的算法流程

优化神经网络的故障定位算法如图3所示，可以分为3个方面：通过遗传算法优化得到网络的初始连接权值和阈值；信号的前向传播和误差的反向传播，即计算实际输出时按从输入到输出的方向进行；权值和阈值的修正从输出到输入的方向进行。

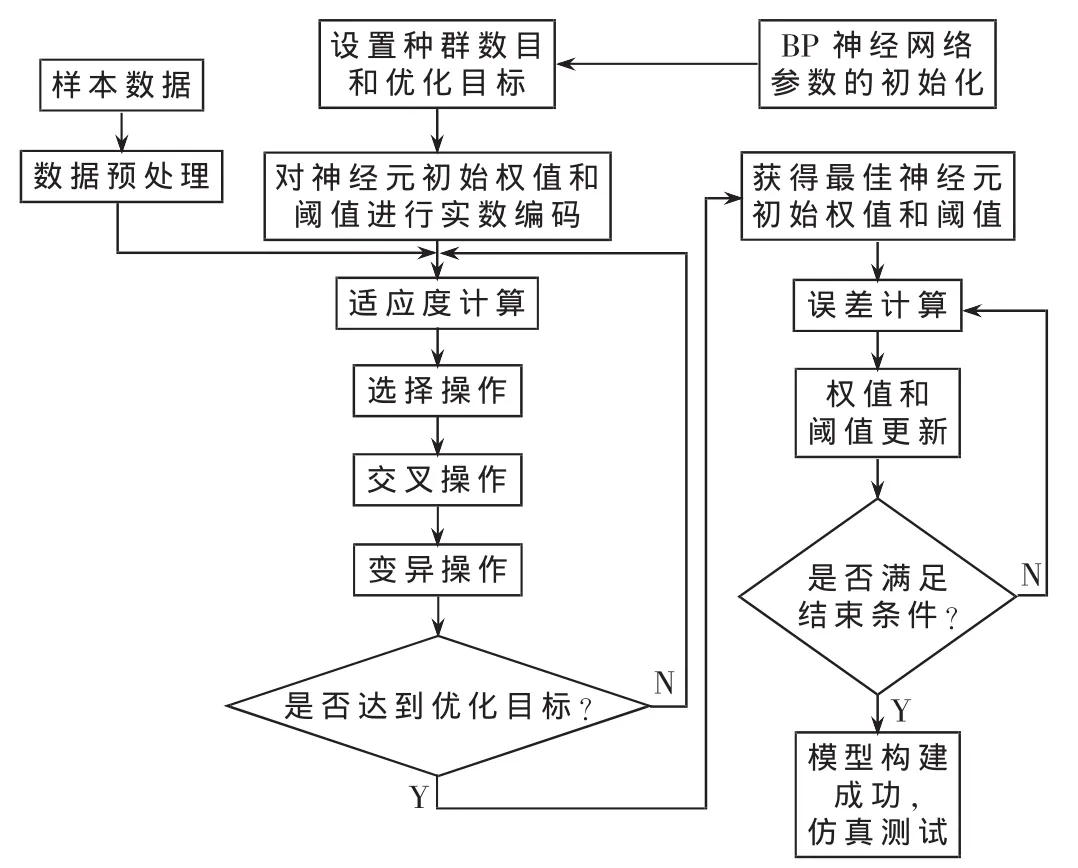
图3 优化神经网络的算法流程图

3.2.1 网络初始连接权值和阈值的获得

遗传算法是一种全局寻优搜索算法。它将问题空间中的可能解看作是群体里的类似于染色体的个体，并将每一个个体编码成符号串的形式。按照适应度函数计算出函数值，然后依据函数值进行选择、交叉、变异等操作，不断进化并得到最优解。遗传算法优化步骤如下：

（1）初始化种群P，包括交叉规模、交叉概率Pc、突变概率Pm并对输入层与隐含层的权值和隐含层与输出层的权值初始化；在编码中，采用实数进行编码，并初始化种群。

（2）计算每一个个体评价函数，并将其排序。可按下式概率值选择网络个体：

其中fi为个体i适配值，可用误差平方和E来衡量，即：

其中i=1，…，N表示染色体数；k为输出层节点数；p为学习样本数；Tk为教师信号。

（3）以概率Pc对个体Gi和Gi+1交叉操作产生新个

（4）利用概率Pm突变产生Gj的新个体G′j。

（5）将新个体插入到种群P中，并计算新个体的评价函数。

（6）如果找到了满意的个体则结束，否则转至步骤(3)。达到指标后将最优个体解码即可得到优化后的网络连接的初始权值和阈值[9]。

3.2.2 信号的前向传播和误差的反向传播

(1)信号的前向传播过程，即实际输出从输入到输出的方向进行。

隐含层第i个节点的输入neti：

隐含层第i个节点的输出yi：

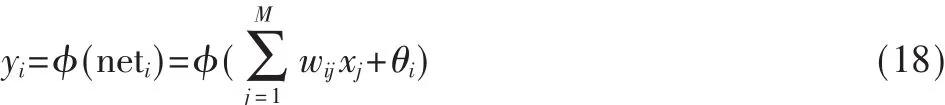
输出层第k个节点的输入netk：

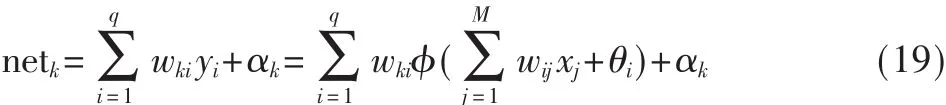
输出

层第k个节点的输出ok：

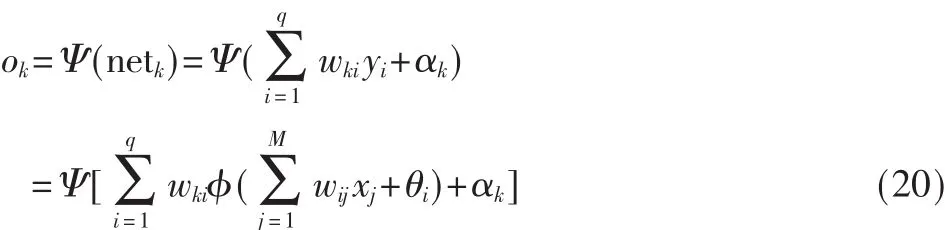
(2)误差的反向传播，即首先由输出层开始逐层计算各层神经元的输出误差，然后根据误差梯度下降法来调节各层的权值和阈值，使修改后的网络的最终输出能接近期望值。

对每一个样本p的二次型误差准则函数为：

系统对P个训练样本的总误差准则函数为：

3.2.3 权值和阈值的修正过程

根据误差梯度下降法依次修正输出层权值的修正量Δwki、输出层阈值的修正量Δαk、隐含层权值的修正量Δwij、隐含层阈值的修正量Δθi。

输出层权值调整公式：

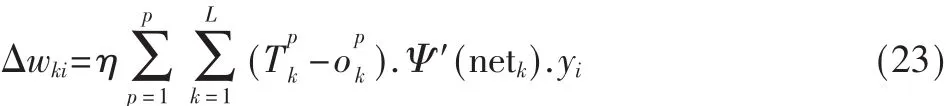
输出层阈值调整公式：

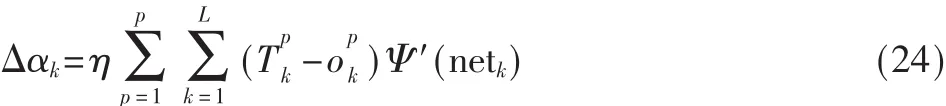
隐含层权值调整公式：

隐含层阈值调整公式

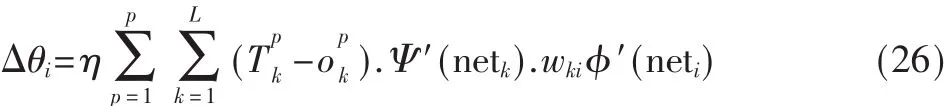
4 仿真分析

本文采用Simulink构建10 kV中性点不接地系统单相接地故障模型。三相电源为Y型连接，中性点不接地。线路参数：正序阻抗z1=(0.17+j0.38)Ω/km，正序容纳为3.045 μs/km，零序阻抗为0.23+j1.72 Ω/km，零序容纳为1.884 μs/km，采样频率为5 kHz。3条线路长度分别为20 kM、100 kM、100 kM。以第一条线路A相接地为实验，从1 kM起，每次增加1 kM，直到9 kM，并且以3种情况作为横向标准：相角0°，故障电阻50 Ω；相角0°，故障电阻500 Ω；相角45°，故障电阻50 Ω。得到每个标准下故障时线路的零序电流和母线零序电压，转换成.mat文件，放入Matlab的工作空间进行Morlet复小波变换。由此得到它们模极大值的实部和虚部并作为输入训练样本，实际故障距离作为输出训练样本。对遗传算法优化过的神经网络进行训练，训练好之后采用测试样本进行测试，把输出反归一化，得到故障线路距离的测试结果，并计算得到相对误差百分比，结果如表1所示。

由表1可以看出，小波优化神经网络已经良好地拟合了输入故障特征与故障点位置之间的映射，说明小波优化神经网络能够很好地进行故障定位，3种标准下测试距离的相对误差在1.5%以下。之所以能达到这么高的精度，一是因为10 kV的小电流接地系统一般为面向用户的单电源系统，大多数参数可知；二是因为小波模极大值能够很好地反映故障特征；三是因为遗传算法的寻优能力和神经网络良好的非线性拟合能力。并且通过横向标准可以得出这种故障定位方法基本不受故障点位置、故障点电阻、相角的影响。

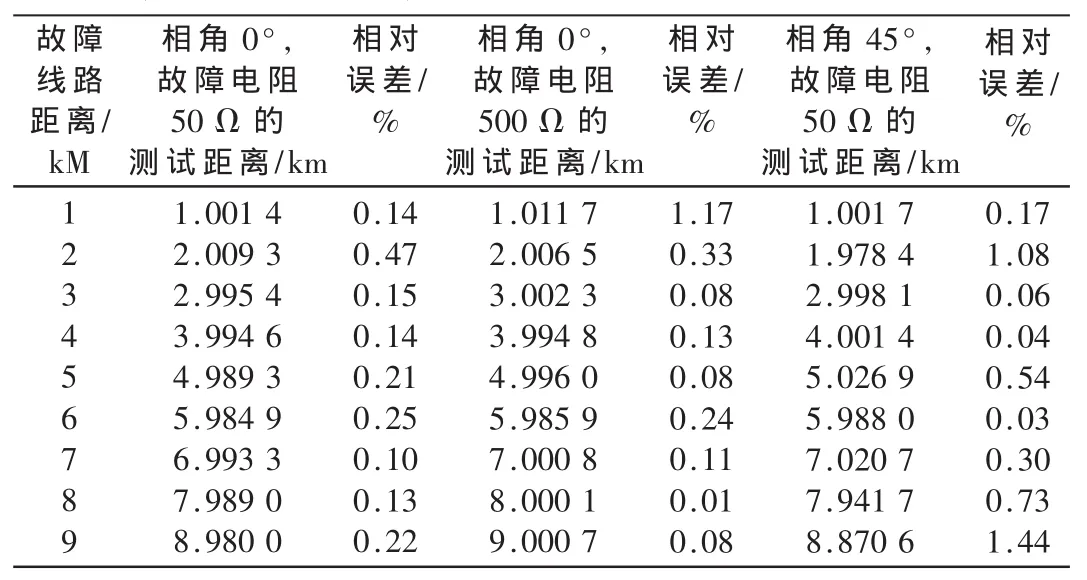
表1 各个标准下的测试结果和相对误差

小波变换作为一种现代信号处理方式，非常适合于分析电力系统的暂态过程，再结合神经网络输入/输出的良好非线性映射能力以及遗传算法良好的寻优能力，完成对故障的精确定位。测试结果表明，定位相对误差非常小(不超过3%)，并且不受故障点位置、故障点电阻及相角的影响。除此之外，遗传算法使神经网络避免陷入局部最小问题，加快了网络的运算速度,同时遗传算法还可以对神经网络的学习规则进行优化，值得进一步研究。

参考文献

[1]CHAARI O，MEUNIER M，BROUAYE F.Wavelets：a new tool for the resonant grounded power distribution systems relaying[J].IEEE Transactions on Power Delivery，1996，11(3)：1301-1308.

[2]Yao Xin.A review of evolutionary artificial neural networks[J].International Journal of Intelligent Systems，1993，8(4)：539-567.

[3]程杰.周源.基于“S”注入法的小电流接地系统单相接地故障定位方案研究[J].中国科技博览，2009(13)：86-87.

[4]严凤，杨奇逊，齐郑，等.基于行波理论的配电网故障定位方法的研究[J].中国电机工程学报，2004，24(9)：37-43.

[5]夏雨，贾俊国，靖晓平，等.基于新型配电自动化开关的馈线单相接地故障区段定位和隔离方法[J].中国电机工程学报，2003，23(1)：102-106.

[6]张耘川，苏宏升.基于暂态行波的小电流接地系统故障定位[J].电测与仪表，2013(2)：5-9.

[7]吕永霞.基于小波奇异性检测的电力系统故障检测[J].吉林大学学报（信息科学报），2009，27(2)：156-161.

[8]董天祯，郭江鸿，吕娟，等.基于神经网络的输电线路故障检测研究[J].系统仿真学报，2009，21(15)：4903-4906，4911.

[9]PAN H．Application of BP neural network based on geneticalgorithm[J]．Computer Application，2005，25(12)：2777-2779.