基于模糊神经网络的小电流接地系统单相接地故障定位研究
肖 波,张 显,王西伟,刘 君
(1.贵州师范大学机电工程学院,贵州贵阳 550002;2.贵州黔源电力股份有限公司,贵州贵阳 550002;3.福建省电力有限公司漳州电业局,福建漳州 363000;4.贵州电力试验研究院,贵州贵阳 550002)
0 引言
我国10~35 kV配电网一般为小电流接地系统,在分支繁多、接线复杂的树状配电网中,单相接地故障是发生机率最高的一种故障,其概率为80%左右。当系统发生单相接地故障时,可能会引起系统的过电压,损坏电气设备,破坏系统的安全稳定运行,因此必须尽快采取措施完成故障定位,及时从系统中切除故障[1-3]。
利用基于梯度的神经-模糊学习算法的非线性逼近能力,根据故障后继电保护装置安装处测得故障后第一周期的三相电压(Vabc)、电流(Iabc)以及用来判断接地故障的零序电流基频分量作为模糊神经网络的输入,构造了一个由输入层、语言项层、规则层、输出层组成的模糊神经网络实现准确的故障定位。
1 基于神经网络的模糊系统
文献[4]用神经网络来实现0阶Takagi-Sugeno模糊系统,使得该系统具有自适应学习能力。其网络拓扑结构如图1所示,它是一个具有m个输入变量x=(x1,x2,…,xm)∈Rm和一个输出变量y∈R的四层网络。
0阶Takagi-Sugeno模糊系统的模糊规则库定义如下:
Rulei:IFx1isA1iandx2isA2iand …andxmisAmiTHENyisyi.

图1 基于神经网络的模糊系统网络图
其中i表示相应的第i条规则,i=1,2,…,n;n为模糊规则的条数;yi是输出空间上的1个实数;Ali是xl的1个模糊子集;Ali(xl)是模糊论断“xlisAli”的高斯型隶属函数,定义如下:
(1)
式中ali和σli分别为Ali(xl)的中心和宽度。
给定输入x=(x1,x2,…,xm)∈Rm,根据0阶Takagi-Sugeno模糊系统,网络各层及相应节点的功能如下:
(1)输入层:该层的每个节点表示一个输入变量,并直接将输入变量转到下一层。
(2)语言项层:该层也被称为隶属函数层,它的每个节点表示一个语言变量的隶属函数,文中使用高斯函数作为每个语言变量的隶属函数。把高斯函数的中心和宽度当作连接输入层到该层的权值。
(3)规则层:该层的节点称作规则节点,每个节点代表一条模糊规则。该层将模糊推理的前件部分和结论部分连接起来,在逻辑上实现两者之间的联系。第i个规则节点的输出为
(2)
规则层不存在对权值的调整问题,把语言项层到该层的连接权看作常数1。
(4)输出层:所有规则节点都通过结论连接线连入到输出节点上,并被直接解释成输出强度。该层完成重心法去模糊化操作,以得到数值型输出:
(3)
将结论参数yi看作连接上一层到本层的连接权值。
2 改进的基于梯度的神经-模糊学习算法
传统的基于梯度的神经-模糊学习算法是求网络误差函数E关于高斯隶属函数宽度σli的梯度。文中提出的改进学习算法是将高斯隶属函数宽度σli的倒数bli看作独立变量,求网络误差函数E关于bli的梯度。这一简单的改进,使得在求梯度的过程中避免了对分母中的变量求偏导,从而减少了求误差函数关于权值梯度的计算量,提高了网络的学习效率。
令bli=1/σli,将式(2)化为:
l=1,2,…m;
i=1,2,…,n
(4)
于是
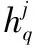
(5)
给定网络的初始权值W0以及常学习率η>0,权值向量的迭代公式为:
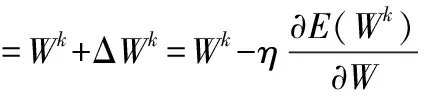
k=0,1,2…
(6)
网络误差函数E(W)关于权值向量W的梯度计算如下:
(7)
这里,误差函数E(W)关于向量a0的梯度为
(8)

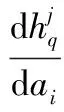
(9)
并且:
(10)
(11)
式中:oj为第j个训练样本xj的理想输出;yj为其相应模糊推理的实际输出。
由式(9)、式(10)以及式(11)可以得到,对1≤i≤n,网络误差函数E(W)关于向量ai的梯度为:
(12)
类似可得,对任意1≤i≤n,网络误差函数E(W)关于向量bi的梯度为:
(13)
3 仿真分析
仿真使用MATLAB/Simulink7.0软件来模拟小电流接地系统单相接地故障,所采用的系统结构如图2所示。线路参数:正序阻抗为0.15+j0.35 Ω/km,正序容纳为3.050 μs/km,零序阻抗为0.21+j1.75 Ω/km,零序容纳为1.894 μs/km.4条10 kV馈线长度分别为8 km、9.5 km、15.5 km、11.5 km.

图2 小电流接地系统仿真模型
表1是利用改进的基于梯度的神经-模糊学习算法,在不同过渡电阻、不同故障点下的仿真结果。从表1可看出,除个别点外,各故障点的相对误差小于0.5%,绝对误差在10 m以内的占95.56%,其余都在15 m以内,因此测量精度是可以满足工程要求。在仿真中列出0 Ω,11 Ω和21 Ω 3种过渡电阻的仿真结果,结果证明采取这种措施后,过渡电阻对测量值的影响是不大的。
4 结论
小电流接地系统单相接地故障定位问题是多年来一直未能解决的一个难题,模糊神经网络作为一种现代信号处理方法,非常适合分析电力系统故障过程。文中提出的使神经网络作为一种现代信号处理方法,非常适合分析电力系统故障过程。文中提出的使用改进的基于梯度的神经-模糊学习算法是可行的,该方法测距精度比较高,测距精度受过渡电阻的影响较小,具有一定的实用价值。
参考文献:
[1]李振然,贾旭彩,李滨.基于小波变换与BP神经网络相结合的配电网单相接地故障定位方法.继电器,2004,32(9):24-26;34.
[2]刘凤霞,刘前进.基于模糊神经网络的故障测距.电力自动化设备,2006,26(5):32-34;74.

表1 使用改进的基于梯度的神经-模糊学习算法进行故障定位的仿真结果
[3]张利,夏楠,姜彤.中性点不接地系统单相接地故障的定位方法.电力系统及其自动化学报,2010,22(4):36-40.
[4]WU W,LI L,YANG J,et al.A modified gradient-based neuro-fuzzy learning algorithm and its convergence.Information Sciences,2010,180(9):1630-1642.

