一类非线性中立型变延迟积分微分方程的稳定性分析

丛玉豪, 卢翠翠, 蒋成香

(1.上海师范大学 数理学院, 上海 200234; 2.上海师范大学 天华学院, 上海 201815)

0 引 言

泛函微分方程在许多科学领域中都有着广泛的应用,例如物理学、工程学、生物学、医学和经济学等[1].其理论解一般很难得到,数值解和数值稳定性研究在方程求解中占有十分重要的地位.近30年来,对延迟微分方程,中立型延迟微分方程,延迟积分微分方程等类型的泛函微分方程的研究,取得了大量的研究成果[2-14].

近些年来,关于非线性中立型延迟积分微分方程理论解和数值方法的稳定性开始被学者们关注,文献[12]对非线性中立型泛函微分方程的理论解和数值解的稳定性作了研究,文献[13～14]研究了θ-方法、一般线性方法求解非线性中立型延迟积分微分方程线性的渐近稳定性.本文作者考虑如下一类特殊的非线性中立型变延迟积分微分方程的稳定性：

(1)

这里F是复值连续函数，φ(t)是连续可微复值函数，τ(t)是连续滞时函数，积分项中g为关于t的连续函数， 且满足条件:

A: 对∀t≥t0，τ(t) ≥τ0>0，且α(t)=t-τ(t) 是严格递增的.

文中作者首先针对非线性中立型变延迟积分微分方程的模型方程(1),给出方程理论解稳定的条件并给予了证明；其次研究了线性θ-方法求解非线性中立型变延迟积分微分方程的数值稳定性,证明了A-稳定的θ-方法求解非线性中立型变延迟积分微分方程是稳定的.

1 方程理论解的稳定性分析

设 〈·,·〉为向量空间CN中的内积,‖ ·‖是由该内积导出的范数.为了讨论问题(1)的稳定性,引入与其相应的如下扰动方程：

(2)

这里ψ(t)是连续可微的复值函数.假设方程(1)和(2)分别恒有唯一的真解y(t)和z(t),并设F为[t0,+∞)×CN×CN×CN×CN→CN上关于t的连续函数,且满足如下的条件：

Re〈y1-y2,F(t,y1,u,v,w)-F(t,y2,u,v,w) 〉≤R(t) ‖y1-y2‖2,∀t≥t0,y1,y2,u,v,w∈CN,

‖F(t,y,u1,v,w)-F(t,y,u2,v,w) ‖ ≤β1(t) ‖u1-u2‖ ,∀t≥t0,y,u1,u2,v,w∈CN,

‖F(t,y,u,v1,w)-F(t,y,u,v2,w) ‖ ≤β2(t) ‖v1-v2‖ ,∀t≥t0,y,u,v1,v2,w∈CN,

‖F(t,y,u,v,w1)-F(t,y,u,v,w2) ‖ ≤β3(t) ‖w1-w2‖ ,∀t≥t0,y,u,v,w1,w2∈CN,

‖g(t,ξ,y1)-g(t,ξ,y2) ‖ ≤β4(t) ‖y1-y2‖ ,∀t≥t0,ξ∈R,y1,y2∈CN.

(3)

因为函数F的特殊性,考虑函数：

H(t,y,u,v,j,w)=F(t,y,u,F(α(t),u,v,j,w),w).

类似于F,恒有假设H关于t连续,且关于u一致Lipschitz连续,即存在连续函数σ(t),使得

‖H(t,y,u1,v,j,w)-H(t,y,u2,v,j,w)‖ ≤σ(t) ‖u1-u2‖, ∀t≥t0,y,u1,u2,v,j,w∈CN.

(4)

求解方程(1)和(2)的方法采用分步法,因此,需要确定理论解y(t)的断点,这些点是与y′(t)的不连续性联系在一起的.令ξ0=t0,因为α(t)满足条件A,所以存在唯一解ξ1满足α(ξ)=ξ0,从而有

ξ0=t0<ξ1<…<ξn<ξn+1<…,

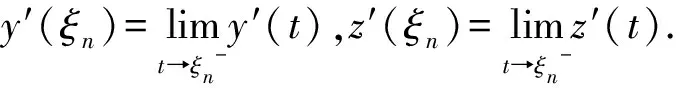
引理1.1[9]若对于实函数Y(t),R(t),Γ(t)有

(5)

则当R(t)<0,∀t≥t*时,有

(6)

定理1.1若方程(1)和(2)满足条件(3)及对∀t≥t0,R(t)<0,则当

(7)

时,方程(1)和(2)的理论解满足

‖y(t)-z(t)‖≤max {‖φ(t0)-ψ(t0)‖,k},

(8)

其中k=

(9)

即方程(1)的理论解是稳定的.

证明由条件(3)的第一式可得:

其中

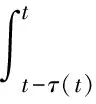
应用引理1.1,可得:

(10)

接下来,将在区间In上逐步地分析方程(1)和(2)的解,考虑当n≥ 1时区间In=:[ξn-1,ξn].

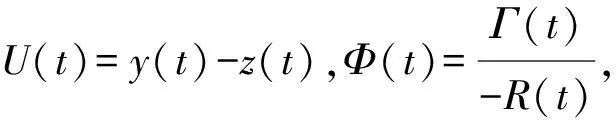
(11)

(12)

当n=1时,

由条件(3),(4),且因为当t∈I1时,s∈I1,α(s)∈I0,所以

(13)

由(12)和(13),可得:

‖U(t)‖≤ max{‖φ(t0)-ψ(t0)‖,k}, ∀t∈I1.

(14)

当n≥2时,由条件(3)可得:

所以

由条件(7)得:

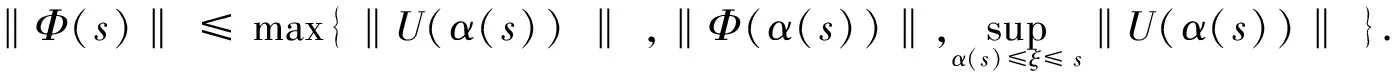
(15)

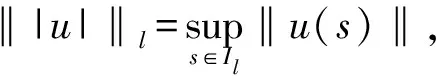
‖|Φ|‖n≤max{‖|u|‖n-1,‖|Φ|‖n-1},n≥2,

(16)

对任意的n≥ 1,定义vn=max{‖|u|‖n,‖|Φ|‖n},则(12)可表示为:

‖|u|‖n≤max{‖|u|‖n-1,‖|Φ|‖n-1},n≥1.

(17)

由(16)和(17)可得vn≤vn-1,n≥ 1,‖|u|‖n≤v1.

当n=1时,由(16)和(17)可得:

‖|Φ|‖1≤κ, ‖|u|‖1≤ max{‖φ(t0)-ψ(t0)‖,κ},

所以由上式可得:

v1≤ max{‖φ(t0)-ψ(t0)‖,κ},

所以对∀t≥t0,有:

‖y(t)-z(t) ‖ ≤max{ ‖φ(t0)-ψ(t0) ‖,κ}.

即定理成立.

2 线性θ-方法的数值稳定性

考虑如下线性θ-方法：

yn+1=yn+h[θf(tn+1,yn+1)+(1-θ)f(tn,yn)],

(18)

(18)求解方程(1),可得:

(19)

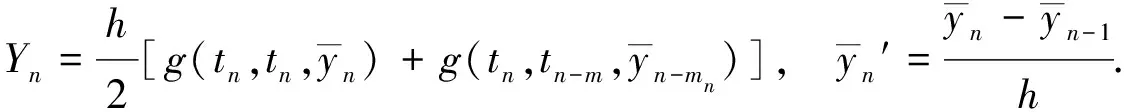
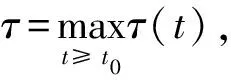
-m≤n-mn

将方法(18)用于求解扰动方程(2),可得:

(20)

以下的证明假设R(t),β1(t),β2(t),β3(t),β4(t)均为大于或等于0的连续有界函数,且

(21)

定义2.1线性θ-方法用于求解方程(1)称为稳定的,如果该方法用于求解满足条件(3)和条件(4)的初值问题方程(1)和(2)时,对∀h>0,有:

其中C1、C2为常数.

wn+1=wn+hθQn+1+h(1-θ)Qn.

上式变形并两边作内积,可得：

‖wn+1‖2+h2θ2‖Qn+1‖2=‖wn‖2+h2(1-θ)2‖Qn‖2+

2hθRe〈wn+1,Qn+1〉+2h(1-θ) Re〈wn,Qn〉.

(22)

所以由条件(3)和条件(21) 可得:

(23)

同理可得:

(24)

利用上式递推下去可得:

由上式知易得:

即定理2.1成立,这说明线性θ-方法求解方程是数值稳定的.

参考文献:

[1] HALE J K.Theory of functional differential equations[M].New York：springer-verlag，1977.

[2] HU G,MITISUI T.Stability of numerical methods for systems of natural delay differential equations[J].BIT,1995,35(4):504-515.

[3] ZENNARO M.P-stability of Runge-Kutta methods for delay differential equations[J].Numer Math,1986,49:305-318.

[4] LIU M Z,SPIJKER M N.The Stability of the -methods in the Numerical Solution of Delay Differential Equations[J].IMA Journal of Numerical Analysis,1990,10:31-48.

[5] CONG Y H,CAI J N,KUANG J X.The GPL-stability of Rosen-brock methods for delay differential equation[J].Applied Mathematics and Computation,2004,150:533-542.

[6] HUANG C M,FU H Y,LI S F,et al.Stability analysis of Runge-Kutta methods for non-linear delay differential equations[J].BIT,1999,39：270-280.

[7] ZHANG C J,VANDEWALLE S.Stability analysis of Runge-Kutta methods for nonlinear Volterra delay integro-differential equations[J].IMA J Numer Anal,2004,24：193-214.

[8] TIAN H J,KUANG J X.The numerical stability of linear multistep methods for delay differential equations with many delays[J].SIAM Numer Anai,1996,33(3):883-889.

[9] 王晚生,李寿佛.非线性中立型延迟微分方程稳定性分析[J].Mathematica Numerica Sinica,2004,26(3):303-314.

[10] 余越听,文立平,李寿佛.延迟积分微分方程单支方法的稳定性分析[J].工程数学学报,2008,25:469-474.

[11] ZHAO J J,XU Y,LIU M Z.Stability analysis of numerical methods for linear neutral Volterra delay integro differential equations[J].Appl Math Comput,2005,167(2):1062-1079.

[12] 王晚生,李寿佛.非线性中立型泛函微分方程数值分析[D].湘潭:湘潭大学,2008.

[13] 余越昕,文立平.非线性中立型延迟积分微分方程线性θ-方法的渐近稳定性[J].数值计算与计算机应用,2009,30(4):241-246.

[14] 余越昕.非线性中立型延迟积分微分方程一般线性方法的稳定性分析[J].Mathematica Numerica Sinica,2010,32(2):125-134.