基于解释结构模型的我国高等教育质量影响因素分析
陈 藏,荣 贺
(1.华北科技学院,北京东燕郊 101601;2.北京市顺义牛栏山第一中学,北京 101301)
0 引言
教育是推动经济发展和社会进步的重要力量,正确认识我国高等教育的现状与发展趋势,分析影响我国高等教育发展的因素,有利于我们扬长避短,采取措施来推动我国高等教育加快向国际接轨,加快步入教育强国的步伐。
随着我国科教兴国观念不断深入人心,高等教育已成为国家科技进步、经济发展的重要支撑。近年来,我国高等教育快速发展。对比学校每年招收学生的人数数量,我们可以明显看出,由于我国经济的快速发展,民众对高等教育的需求日趋旺盛。经过几年的连续扩招,中国的高等教育规模已跃居世界第一。种种迹象表明,我国的高等教育已开始由“精英教育”走向“大众化教育”。这符合了世界高等教育发展的趋势。我国高等教育的大众化时代正向我们走来,高校的扩招将持续一个相当长的时期。尽管我国高等教育已经快速发展,并取得了很好的成就,但是提高高等教育的教学质量是个永久的话题。《教育大词典》中,教育质量的概念为“教育水平高低和效果优劣的评价。影响高等教育质量的主要因素包括学校管理制度、教学计划、教学内容、教学方法、教学态度以及学生的学习态度和国家方面政策,主要体现在学生的综合素质上。”高等教育是社会的一个子系统,其质量受很多因素影响,且这些因素是相互联系的。影响高等教育质量的因素很多,这些因素是按照一定的结构存在的,在一定的位置起着一定的作用。
现有文献对于我国高等教育质量的研究很多,对影响高等教育的因素的分类方法也多种多样,其中贾定良提出其影响因素是招生规模、专业设置、教师投入的时间和精力、学生投入的时间和精力[6]。李泽彧,陈杰斌,黄海群将影响高等教育质量的主要因素归纳为高等教育资源水平和利用资源的水平。将这些影响因素概括为以下几个方面:教师、学生、学校管理人员、政府、企业和社会组织等。周扬、张忠华对之前的研究人员的成果进行了相关总结,将影响我国高等教育质量的因素分为六个方面,分别是国家和政府的相关部门、社会、学校、家庭、老师和学生[8]。
本文根据现代我国高等教育的发展情况,找出影响我国高等教育发展的各的因素,采用解释结构模型对这些因素进行分析,最后得出它们的层次关系。
1 解释结构模型简介
解释结构模型法(Interpretative Structural Modelling Method,简称ISM方法),是现代系统工程中广泛应用的一种分析方法,是结构模型化技术的一种。是美国华费尔特教授于1973年作为分析复杂的社会经济系统有关问题的一种方法而开发的。它是将复杂的系统分解为若干子系统要素,利用人们的实践经验和知识以及计算机的帮助,最终构成一个多级递阶的结构模型。此模型以定性分析为主,属于结构模型,可以把模糊不清的思想、看法转化为直观的具有良好结构关系的模型。特别适用于变量众多、关系复杂而结构不清晰的系统分析中,也可用于方案的排序等。它的应用面十分广泛,从能源问题等国际性问题到地区经济开发、企事业甚至个人范围的问题等[10]。解释结构模型是节点和有向边构成的图或树图来描述一个系统的结构。节点用来表示系统的要素,有向边则表示要素间所存在的关系。这种关系随着系统的不同和所分析问题的不同,可理解为“影响”、“取决于”、“先于”、“需要”、“导致”或其他含义。通过解释结构模型,可以分析系统的要素选择是否合理,还可以分析系统要素及其相互关系变化对系统总体的影响等问题。该模型用途广泛,使系统的评价、决策、规划、目标确定等能够依靠结构模型来进行定量分析。其工作程序如下:(1)设定关键问题,形成意识模型; (2)要素之间关系分析;(3)建立邻接矩阵;(4)求出可达矩阵;(5)对可达矩阵进行区域划分; (6)级间划分;(7)形成多级递阶有向图;(8)建立解释结构模型。
2 我国高等教育质量的影响因素
我国现代高等教育的质量是受多个因素综合影响的一个过程,其中学校方面的影响因素包括师资队伍建设、教学资源、育人环境、教学改革、教学管理;教师方面的影响因素包括教学方法、教学内容、教学态度、教学能力;家庭方面的影响因素则包括家庭教育、家庭经济条件;学生自身的影响因素为学生心理健康状况、学习态度、学习能力;社会方面的影响因素包括政府拨款资金、社会文化、国家政策。因此,在我国高等教育质量的影响因素的分析过程中,应综合考虑各方面因素。下面通过表格分析这些因素对我国高等教育质量的影响。
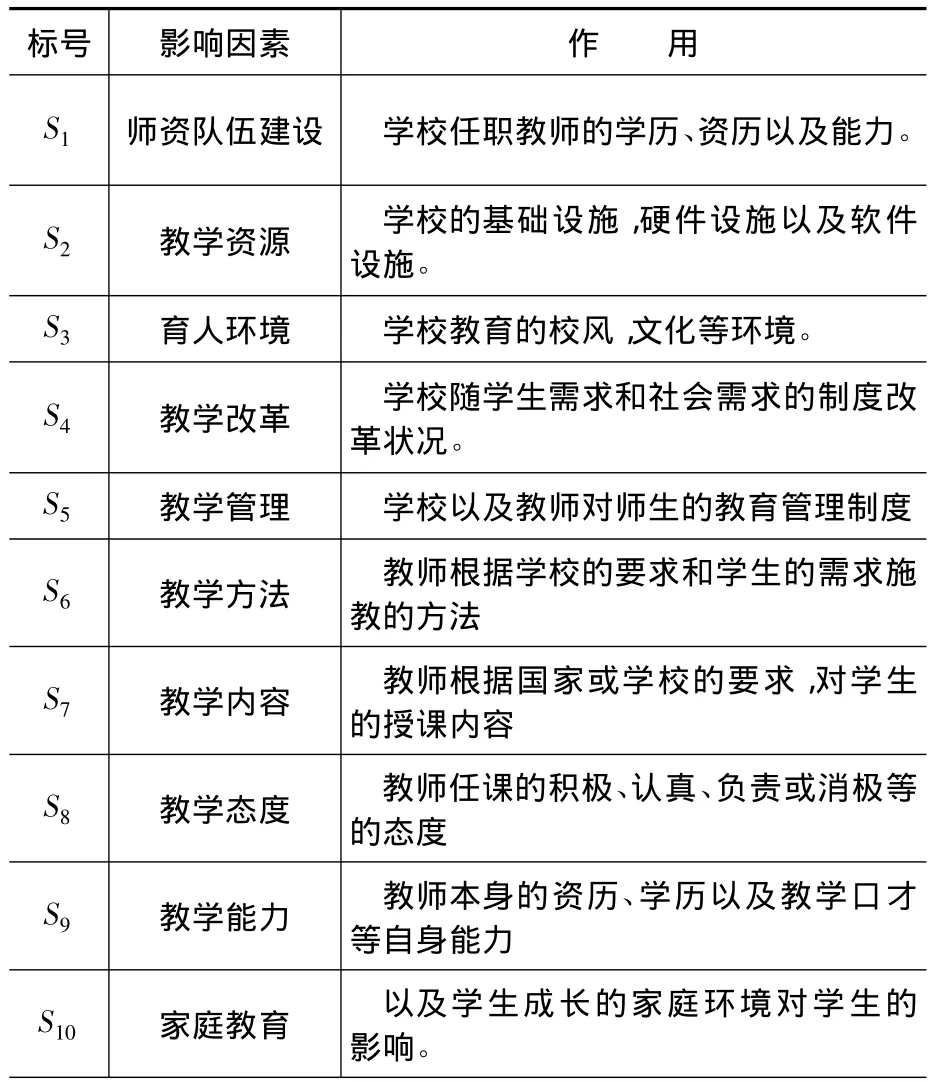
表1 我国高等教育质量的影响因素

续表
以上这些因素有些相互交叉、互为关联,更多的则表现为影响系统中的十分复杂的递阶因素链,因而增加了对影响因素分析的难度。为了理清影响我国高等教育质量诸多因素之间的层次关系,并在此基础上确定其中的深层次的关键影响因素,本文通过建立系统解释结构模型(ISM)来对其作进一步的分析。本文罗列影响因素之间的逻辑关系用下图1表示,其中“C”表示列对行有影响;“R”表示行对列有影响;“V”表示双向影响关系。
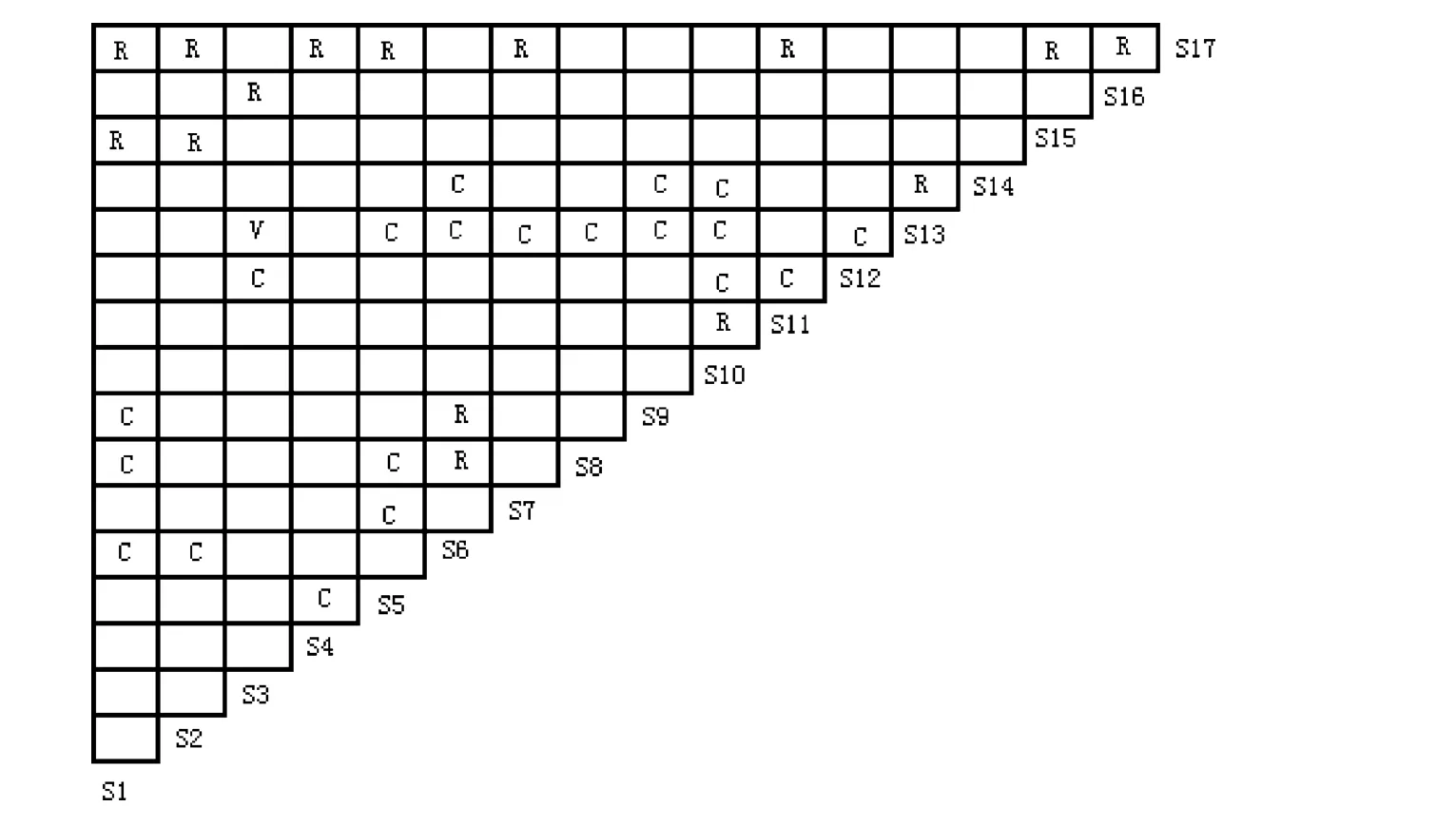
图1 因素关系方格图

图2 可达矩阵
3 建立解释结构模型
解释结构模型的建立需要借助于可达矩阵,可达矩阵反映的是要素之间还存在间接关系。如Si对Sj有影响,Sj对Sk有影响,那么Si对Sk有间接影响。矩阵的元素aij表示因素Si对Sj有间接的影响,否则aij=0。从图1可以得到系统因素的可达矩阵如上图2。
3.1 对可达矩阵进行区域划分
所谓区域划分,就是把要素之间的关系分为可达与不可达,判断哪些要素是连通的,即把系统分为有关系的几个部分或子部分。找出各个元素的可达集P、先行集Q以及两者的交集N。
求解P(Si):可达矩阵中要素Si对应的行中,包含有1的矩阵元素所对应的列要素的集合。代表要素Si可以到达的要素;求解Q(Si):可达矩阵中要素Si对应的列中,包含有1的矩阵元素所对应的行要素的集合。代表可以到达要素Si的要素;求解N(Si)=P(Si)∩Q(Si)。为了对可达矩阵进行区域划分,首先先把可达集合与先行集合及其交集列出在表上,如表2所示。
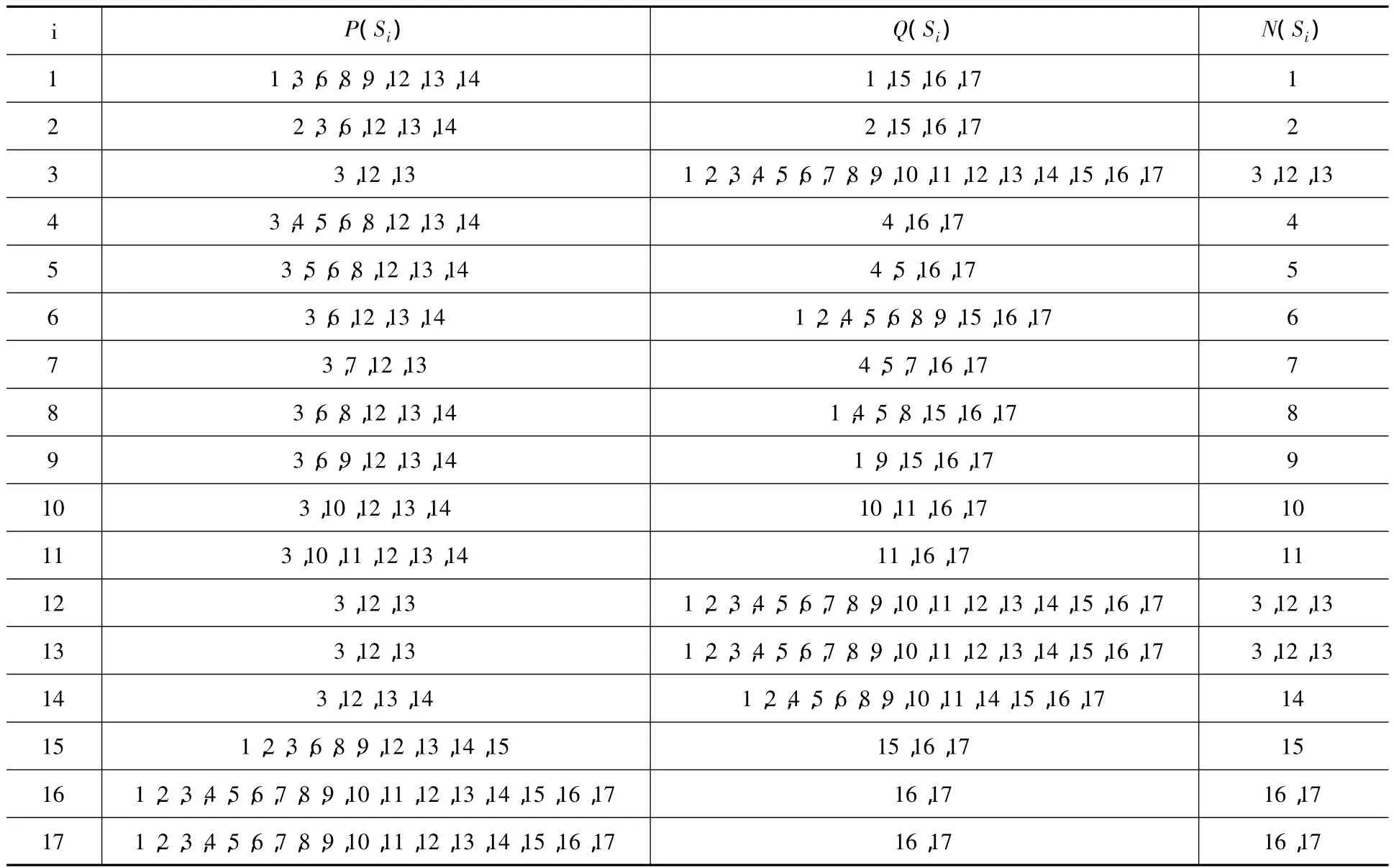
表2 各元素的可达集合与先行集合及其交集表
其次,求出满足N(Si)=Q(Si)的Si构成的集合T,即求出底层要素的集合。由表2可知,T= {S16,S17}。再其次,找出与这些要素在同一部分的要素。如果两要素Si,Sj在同一部分内,则它们的可达集有共同的单元,即P(Si)∩P(Si)≠Φ。否则,它们分别属于两个连通域。最后,根据Si,Sj与共同集合T进行连通域划分,Si,Sj属于一个连通域。经过划分,得出最底层的要素为S16,S17,并由分部划分可知,系统结构可分为一个连通域。
3.2 级间划分
级间划分的目的:是为了更清晰的了解系统中各要素之间的层级关系,最顶层表示系统的最终目标,往下各层分别是表示上一层的原因。利用这种方法,我们可以科学地建立教学过程或其它问题的类比模型。级间划分的方法:是根据N (Si)=P(Si)∩Q(Si)条件来进行层级的抽取。如表2中i=3、i=12和i=13满足条件,这表示S3、S12和S13为该系统的最顶层,也就是系统的最终目标。然后,把表中有关3,12,13的要素都抽取掉,得到表3:

表3 抽出3,12,13后的结果
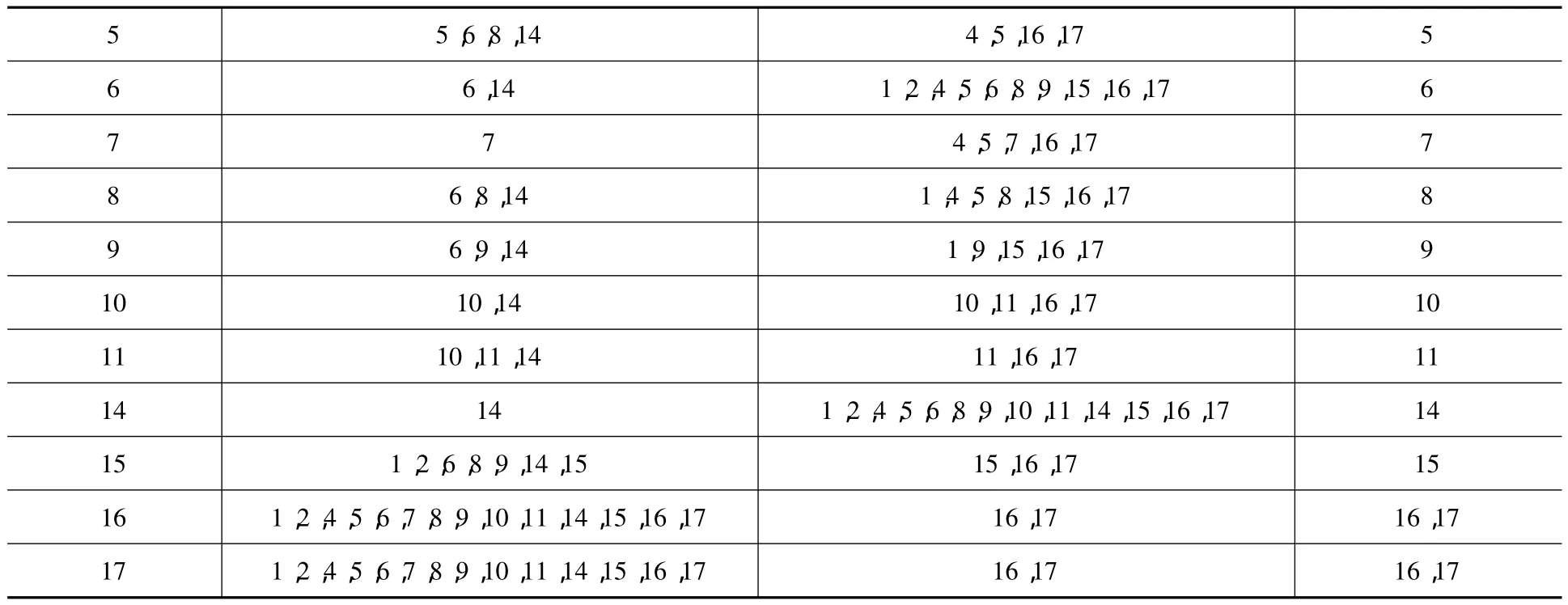
续表
从表3中可以发现i=7和i=14满足条件,即可以抽出7和14,这表示S7和S14为第二层。抽出7和14后得到表4如下:
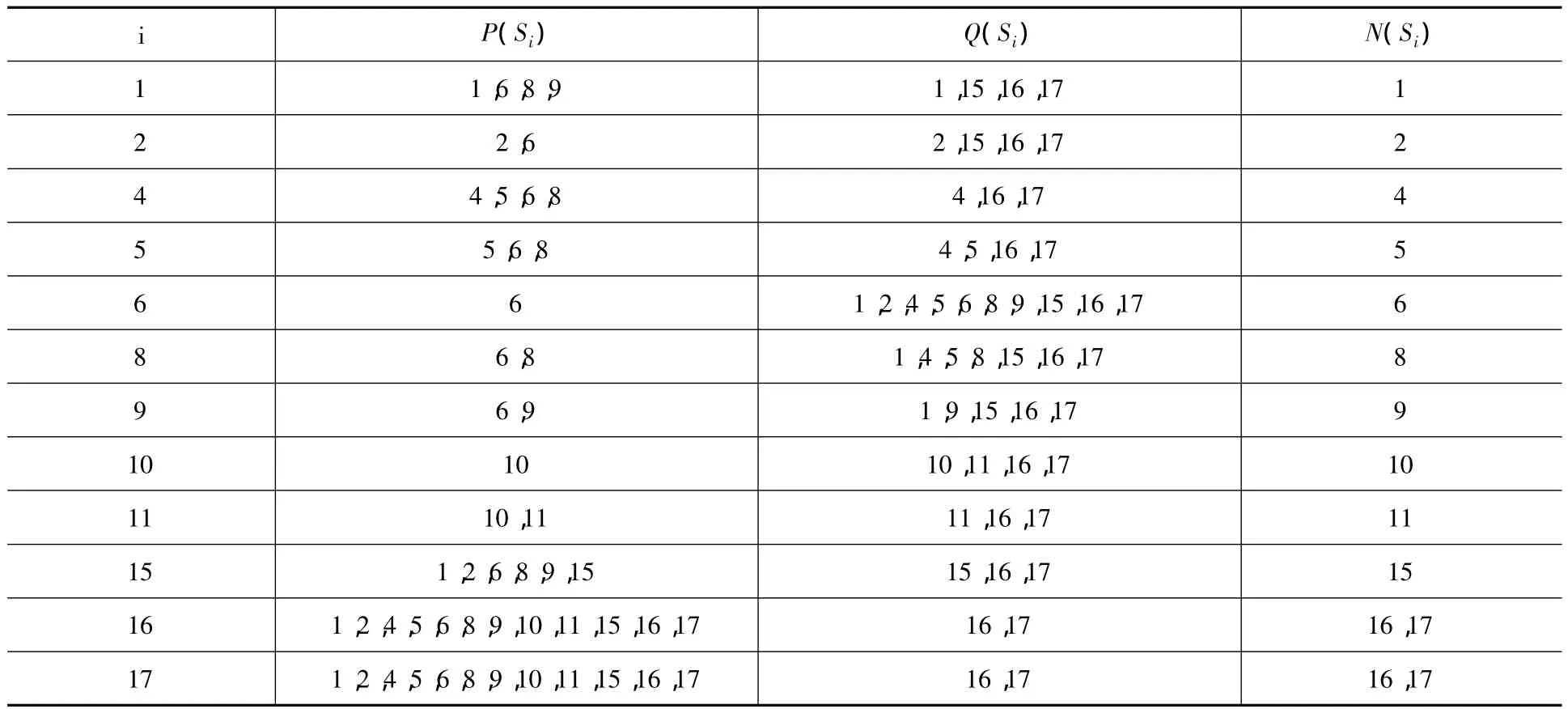
表4 抽出7,14后的结果
从表4中可以发现i=6和i=10满足条件,即可以抽出6和10,这表示S6和S10为第三层。
重复上述步骤可知S2、S8、S9和S11为第四层,S1和S5为第五层,S4和S15为第六层,S16和S17为最低层即第7层。
经过上面的划分,可以构成系统的结构模型。可以看出,影响高等教育的质量的因素可大致分为七层,得到影响我国高等教育质量的因素的解释结构模型如下图4。
从图3可以看出,影响我国高等教育的17个主要因素可以分为7层7类。其中第一类因素是影响我国高等教育质量的直接因素,它从学生在学校的生活环境,学生本身的心理状况,以及学生的学习态度三个方面来揭示一个学校教育成功与否,学生是最为关键的因素之一;第二类因素是揭示提高教育质量与学生综合水平的过程;第三类因素反映了加强教育质量的方法;第四类和第五类因素是提高我国高等教育质量的基础因素,即人,财,物的投入以及管理水平;第六类因素是高等教育发展的依存点;第七类因素是影响我国高等教育质量的根本因素,是提高教育质量的出发点。这七类因素是相互关联,相互依存的,构成了对我国高等教育质量影响的递阶结构关系。
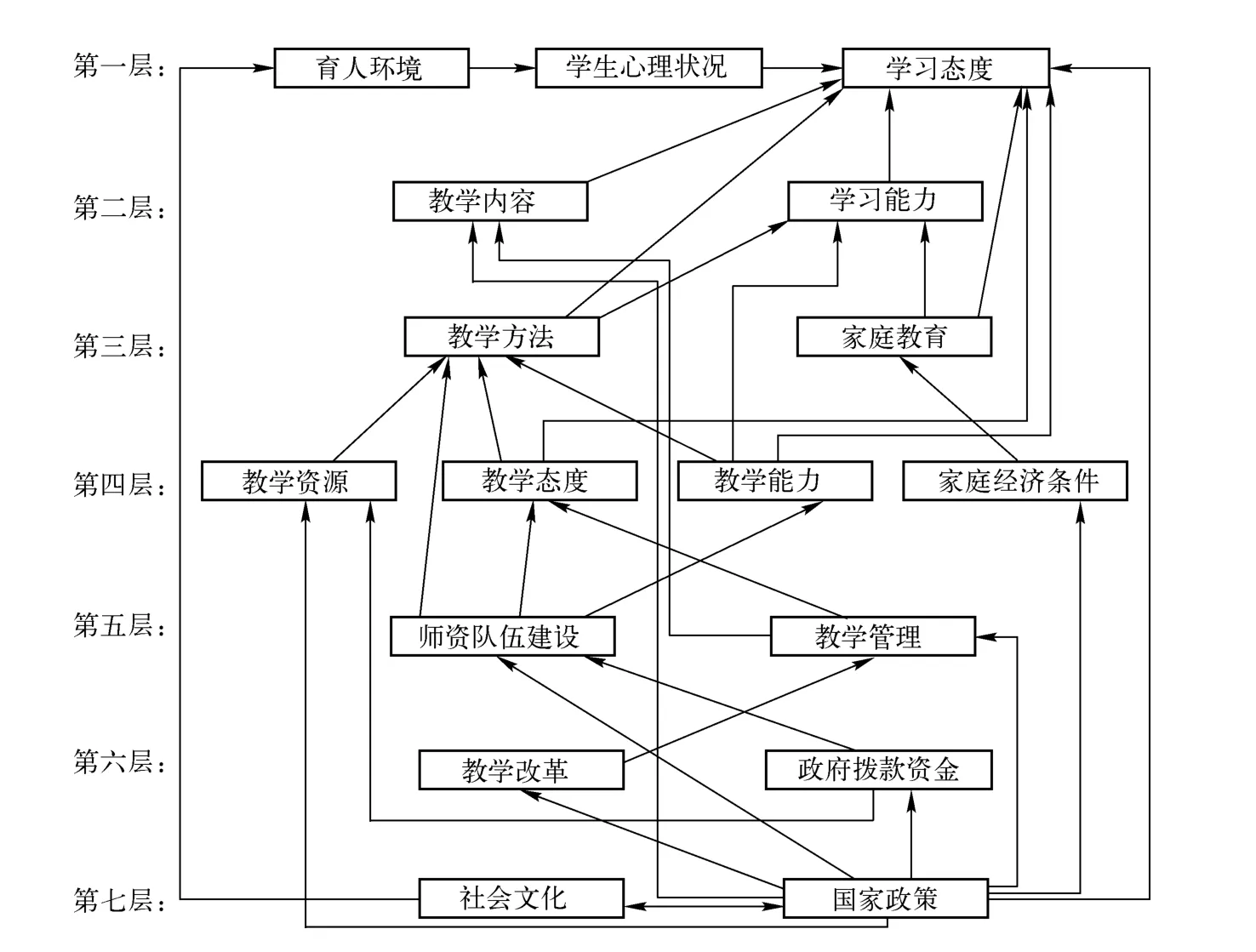
图3 影响我国高等教育质量因素的解释结构模型
[1] 王伟廉.21世纪中国高等教育质量问题分析[J].中国高等教育评估,2001,(3):5-7.
[2] 蓝劲松.构建高等教育质量保证体系[J].科学时报,2001,(6):12-13.
[3] 童康.高等学校内部的教育质量保障与监控体系研究[J].高教探索,2007,(1):36-38.
[4] 贾定良.高等教育质量下降及其对策分析[J].上海高教研究,1997,(12):50-53.
[5] 李泽彧,陈杰斌,黄海群.高等教育质量影响因素新探——基于资源利益相关者及其诉求[J].泉州师范学院学报(社会科学版),2010,1(8):21-25.
[6] 周阳,张忠华.对高等教育质量影响因素的再探讨[J].黑龙江高教研究,2010,(6):12-15.
[7] 章玲,周德群,汤建影.基于DEMATEL方法的高等教育质量的影响因素分析[J].南京航空航天大学学报(社会科学版),2009,3(1):1-3.
[8] 章文杰,解武杰.ISM模型在风险结构分析中的应用[J].商业研究,2002,(1):1-3.

