深基坑围护结构侧向位移变化规律分析研究
刘 冬,曹雪山,刘 兴
(1.河海大学土木与交通学院,江苏南京210098;2.上海隧道工程股份有限公司,上海200062)
基坑开挖是一个卸载的过程,具有竖直方向与水平方向卸载,同时还有应力应变路径问题[1],土体的弹性模量、压缩模量也在变化。在局部卸载过程中,由于存在主动土压力,墙内外的土压力差值在增加[2],会造成地下连续墙产生向坑内的侧向变形。随着开挖深度增加,地下连续墙变形量在增加、变形位置也在变化。上海城建院研究院王印昌[3]在地连墙受力分析中采用了反反分析法,通过弯矩分析得出地连墙变化规律。研究员李刚[4]根据地铁深基坑监测数据给出了变形特征,但二者只研究了地连墙的变形特征,并没给出影响因素以及地连墙的厚度参考值。地连墙的变形量的影响因素众多,其中就有土层的物理性指标、墙体的刚度。本文利用模拟分析软件分析地连墙变形影响因素,并对结果进一步讨论。
1 工程概况
中保站位于南京市鼓楼区河西宁工新寓南门及草场门大街与江东北路交叉口之间,沿草场门大街布置。地面高程为6.70~8.06 m(吴淞高程)潜水稳定水位在1.6~2.5 m,地质属于长江漫滩相沉积地貌单元,水平层理发育,地属秦淮河古河、长江区,土质较为软弱,场地范围内的土层,从上到下主要为杂填土、粉质粘土粉砂互层、粉砂层、粉质粘土层、粉土夹粉砂层、粉砂层、软弱粘土层、粉土夹粉砂层和含卵砾石粉质粘土层,下层34 m左右为基岩。该车站是地铁4号线与9号线的换乘站,两线十字交叉,车站型式为地下两层岛式,基坑开挖方式为半盖挖形式(设施工栈桥板),车站全长525.7 m,车站结构总宽度为23.3 m,设有Φ=800 mm的立柱桩,标准段地连墙埋深39 m,与9号线换乘段坑底埋深约26 m。车站内部结构为钢筋混凝土箱型结构,采用地下连续墙+内支撑的支护结构,采用1 000 mm地下连续墙加6道内支撑支护形式,选取标准段地连墙作为研究对象,地连墙长度约为39 m,进入中风化岩层≥3.0 m。坑底埋深26 m,第一道水平支撑采用900 mm×1 000 mm钢筋混凝土支撑,其余五道采用壁厚为16 mm,直径为609 mm的钢支撑。
2 监测结果对比分析
中保站基坑围护结构采用1.0 m×39.0 m的地下连续墙,插入比为 0.5,地下连续墙入岩为3 m。入岩的地连墙位移量很小,可以忽略不计,而开挖的26 m深度的地连墙作为弹性体,随着坑内外的土应力差值而出现变形。为了研究地下连续墙的变形特性,选择墙体点CXK05(有效深度为 39 m)、CXK06(有效深度为 27 m)与CXK07(有效深度为29 m)号孔作为研究对象。基坑开挖分六次开挖,对于不同开挖深度地连墙变形情况的研究,利用基坑开挖时的各工况(开挖面)为研究断面。CXK05有效测斜深度为39 m,坑底埋深26 m。根据实际监测数据绘制CXK05随基坑开挖深度变化曲线图,如图1:
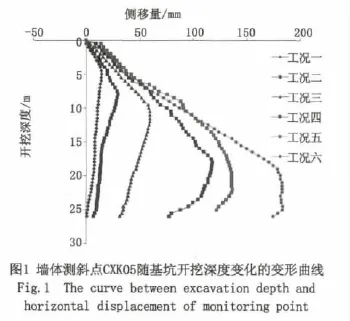
由图1可知,不同工况下,相同开挖深度的地连墙的变形量是不一样的。由工况一知道,地连墙的最大侧向位移量在5 m左右,从0~5 m的位置,地连墙的侧向位移在增大,5~26 m地连墙的侧向位移量在减小。在工况六的时候,这个阶段由于基坑开挖到接近设计基底,这时的基坑内外的侧向土压力差值最大,地连墙作为一个弹性体,这个时候地连墙呈现了“大肚状”,呈类抛物线,最大侧移量为180 mm,处于地连墙的25 m位置。可以看出随着开挖深度增加,地连墙的最大侧移量位置不断下移,表明“土体的侧向应力随着深度的增加而增加”。由此可见地连墙变形量与变形位置具有明显的时空效应。Ou[5]研究台北软土深基坑工程实例,发现具有高稳定性系数的围护结构的最大侧向变形为 0.2%H~0.5%H。CXK05最大水平位移为180 mm,在深度为26 m位置处,最大侧向变形约为0.47%H,略小于Ou统计的台北的0.5%H,这可能是南京与台北的地质不同造成的。
3 基坑围护结构变形数值分析
数据取自中保站基坑标准段靠近中部位置的墙体深层水平位移监测点 CXK05(有效深度39 m)的测斜数据进行统计分析,建立有限元模型按照此监测点所在断面内的基坑实际情况进行模拟。
3.1 有限元模型的建立
采用平面分析软件进行分析,plaxis软件计算简单,使用方便,尤其对于条形基坑具有明显优势。分析时只考虑其一半(左边)。取土层边界长度为525.7 m,约为开挖深度的 20倍,深度为39 m。采用15节点的三角形平面单元模拟岩土体,网格划分为中等粗糙,且对地连墙附近的网格实行局部加密。地连墙采用板单元模拟,支撑看做是弹性体,采用锚定杆来模拟。具体的模拟参数见表1。
由于土具有很强的压缩性,受应力路径与土质影响很大,并且存在塑形形变,所以在plaxis中,选取适用的本构模型很重要。根据徐中华的研究成果,发现HS模型[6]很适用,对于HS模型当中3个压缩模量的的取值,根据王卫东[7]的研究,上海软土地区土体的值为值的 0.9 ~1.3 倍,本文将和的取值都接近于1.2。而则取的 2.8 倍,与 Silty Clay[6]的研究结果相一致。根据所选取的土层参数进行模型建立,模型见图2。

表1中报站基坑土层计算参数Tab.1 Soil parameters of zhongbao pit

3.2 计算结果与监测结果对比分析
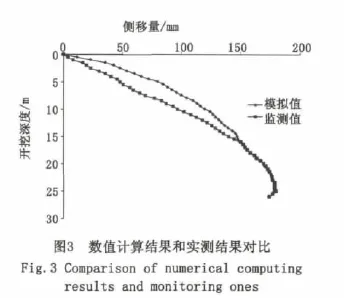
如图3所示,模拟结果显的围护墙体变形曲线大小为178 mm左右,十分接近于180 mm的监测最大位移,且最大位移所在位置与实际监测结果一致,位于地表以下25 m处,高于基坑底面以上1 m。在实际工程施工过程中,测斜在冠梁与混凝土支撑施工完成后进行测量,所以计算结果与实测结果在开始段具有一定的误差,同时施工技术以及土层的物理学指标也不近相同,也是造成开挖到16 m时候有一定区别的原因,在16 m后,计算结果与实测结果基本拟合,这个时候,土的影响参数作为了主要的影响指标,其中就是三个指标。这个时候主要矛盾集中在土的模量上。所以在基坑开挖到一定深度时候,两条曲线就基本拟合了。
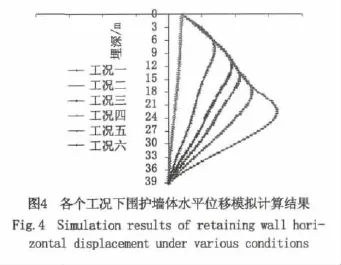
根据不同施工工况下的基坑围护墙体变形模拟结果进行统计分析,得到围护墙体最大水平位移与开挖深度的关系如图4所示。由图可知,所有工况中,围护墙体最大水平位移都位于开挖面附近。工况四与工况五最大侧移量增量最小,分别增加了6 mm与5 mm,因为这两个工况开挖深度的增长率较低,支撑与上一工况支撑的距离较近,而工况二与工况六由于开挖层距离较大,所以最大侧移量增加较多。
此外,由图4还可以看到,每个工况下,处在围护墙体“腹部”以上的水平位移曲线都与下一工况在同一深度范围内的曲线几乎重合,也就是说每一个工况只会改变处在本开挖面附近以及开挖面以下的墙体的水平位移,而对上部的围护墙体变形影响微乎其微。例如工况六,在此工况下,位于围护墙体“腹部”以上曲线基本上是由前面五个工况各自所形成的墙体水平位移曲线叠加而成的,且本次开挖对之前开挖所形成的围护墙体水平位移改变甚微,也就是说位于上一开挖面以上的围护墙体基本不受此次开挖的影响。这说明:基坑自身围护系统对于围护墙体的侧向变形限制作用十分显著。
3.3 影响地连墙最大侧向位移的因素分析
根据统计资料[8]得知,影响地连墙侧移的参数主要有(刚度)、开挖深度、各土层的厚度等。选用控制变量法,假设其他参数条件不变,分别单独改变各个土层土体的HS模型中的三个模量参数的大小。取各个土层的实际值的倍数,分别为实际值的0.3、0.5、0.8、1.0、1.3、1.5、1.8、2.0、2.3、2.5、2.8 倍,然后分别建立有限元模型,将这些模型的计算结果进行有对比分析。结果表明:距离基底较远的土层参数变化对围护墙体最大水平位移位置的影响较小,而地连墙的刚度(厚度)对于地连墙的最大侧移的影响具有明显的区别。
3.4 地下连续墙自身刚度对其最大水平位移影响研究
地连墙的刚度直接取决于地连墙的厚度,其他参数条件不变,只改变地连墙的厚度大小,取一组地连墙厚度为 0.3、0.4、0.5、0.6、0.7、0.8、0.9 m的有限元模型进行研究。根据模拟的结果绘制图5,发现地连墙在不同厚度情况下具有明显变化,围护结构对于基坑变形起到了很大的作用。其中最小值在厚度为1.2 m处,当厚度为0.7 m时候的最大侧移量只比厚度1.2 m增加了20 mm的侧移量,相对增加很少,考虑到地连墙的厚度对于施工难度与经济的影响,建议南京地区的地连墙厚度取0.7~0.9 m,相对于模拟的选取的H,南京市地连墙厚度为地连墙深度的(0.025~0.035)H。

综上所述,在笔者所考虑的众多影响因素中,只有围护墙体自身刚度以及地下各土层强度是决定墙体水平位移最大值所在位置的两个主要因素。本文着重研究了这两种因素对墙体水平位移最大值所在位置的影响程度和变化范围,主要是一些定性的规律分析。至于是否还有一些其他左右墙体水平位移最大值所在位置的因素,本文总结的规律适用于南京,更多的参数影响以及具体参数选取,可以更多的参考国外学者LONG[9]对于参数的研究一文。
4 结论
1)利用plaxi有限元软件的HS模型模拟基坑开挖所得的围护墙变形与实测较为吻合,具有较高的可靠性。
2)发现基坑开挖过程中围护结构变形符合时空效应规律,围护结构侧向变形大小、变形的最大位置变化与分步开挖的空间尺寸及挡墙暴露时间密切相关。
3)发现围护结构随着开挖深度增加,地连墙侧移量在基底附近达到最大值;发现地连墙的变化呈现类似抛物线,地连墙侧向位移随着自身刚度增加增而减小。
4)考虑到地连墙的厚度对于施工难度与经济的影响,建议南京地区的地连墙厚度取0.7~0.9 m,相对于模拟的选取的H,南京市地连墙厚度为地连墙深度的(2.5% ~3.5%)H。
5)围护墙体自身刚度以及地下各土层强度是决定墙体水平位移最大值所在位置的两个主要因素。
[1]胡明辉.深基坑地下连续墙变形及受力特性研究分析[J].山西建筑,2011,37(24):69-70.
[2]刘建航,侯学渊.基坑工程手册[M].北京:中国建筑工业出版社,1997.
[3]王印昌.地下连续墙变形-应力的反分析方法[J].上海市政工程,2008(S1):59-62.
[4]李刚.地铁车站深基坑地下连续墙变形特征分析[J].铁道标准设计,2008,6(24):100-104.
[5]OU C Y,SHIAU B Y,WANG I W.Three-dimensional deformation behavior of the Taipei National Enterprise Center(TNEC)excavation case history[J].Canadian Geotechnical Journal,2000,37(2):438 -448.
[6]徐中华,王卫东.敏感环境下基坑数值分析中土体本构模型的选择[J].岩土力学,2010,31(1):258-264.
[7]王卫东,王浩然,徐中华.基坑开挖数值分析中土体硬化模型参数的试验研究[J].岩土力学,2012,33(8):2283-2290.
[8]张辉,熊巨华,曾英俊.长条形基坑地下连续墙侧向位移数值模拟及其影响因素分析[J].结构工程师,2010,26(1):80-86.
[9]LONG M.Database for retaining wall and ground movements duo to deep excavations[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2001,127(33):203–224.

