地铁事故导致列车延误的社会经济损失评价

王 恺 李晓龙 徐高峻，2

（1.同济大学铁道与城市轨道交通研究院，201804，上海；2.上海轨道交通运营管理中心，200080，上海∥第一作者，硕士研究生）

近年来，地铁运营事故时有发生，造成了不良的社会影响，使得运营安全成为社会和公众关注的焦点和热点。

事故发生后，整条线路上的列车均会受到影响，具体表现为列车的延误时间增加，乘客行程受到影响，从而引起一定的社会经济损失。这些损失称为地铁事故延误社会经济损失。

本文从地铁列车延误对乘客的影响进行分析，建立延误模型，评估地铁事故引起延误的社会经济损失。

1 模型构建

1.1 基本假设

地铁线路上列车密度较大，一旦某列列车发生事故造成一定时间的延误，必然会影响到后续列车，因此，可假设从事故发生的时刻起，全线交通完全中断，直到延误持续时间Tm（Tm＝T1＋T2）后恢复正常的运营状态。其中，T1为线路恢复通车的时间；T2为滞留乘客完全疏散所需要的时间。

对于已到达地铁车站的乘客，由于换乘其他交通方式（如道路公交）会造成大量时间损失，且乘客无法预知线路恢复时间，故实际中乘客更倾向于等待。本文假设事故影响期间该线路的乘客达到率保持原有水平，即乘客不改用其他交通方式。在遇到重大事故，造成线路停运、车站封站或主动疏散乘客的情况时，乘客的延误受疏散组织和地面交通等因素影响，本文论述方法不再适用。

事故延误可能会导致线路内滞留大量乘客，进而在恢复通车时造成线路的临时满负荷状态。线路满负荷时，线路内的乘客数量达到最高值，离开线路的客流也达到最大。假设单位时间到达线路的客流q总是小于满负荷下离开线路的客流Q，即在线路恢复通车后，乘客滞留现象会逐步缓解。

客流在线路上的空间分布是不均匀的，当客流密集区域出现乘客滞留时，即可认为线路处于满负荷运营的状态下，而其他区域的列车运能则有部分闲置。在考量全线列车载运能力时，应考虑客流在空间上的不均匀分布而造成的折减。由于导致大量乘客滞留的事故通常发生在高峰时段，且地铁每日客流相对稳定，故可假设事故线路临时满负荷的客流分布与该线路高峰时段的客流分布相似，则由客流分布不均造成的线路运能折减也近似，可取该线路高峰时段满负荷时的全线列车平均满载率作为线路运能的折减系数β。

1.2 延误模型

当线路恢复通车时，系统内的乘客总数为N′，由事故发生时系统内原有乘客N0和之后陆续到达的乘客N1组成。即：

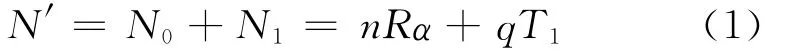
式中：

n——线路上的列车数，列；

R——列车定员数，人／列；

α——当前线路内列车平均满载率；

q——该时段内单位时间进入该线车站的客流，人次／h；

T1——恢复通车时间，h。

全线列车的载运能力为：

式中：

β——运能折减系数；

其余变量同上。

线路恢复通车时，若系统内乘客数量不多（N′≤Nm），乘客均能正常乘车，则可认为该次事故造成的延误影响结束；若系统内乘客数量过多（N′＞Nm），致使恢复通车后仍有部分乘客滞留站台，则认为该次事故造成的延误影响仍在继续。据此，建立2个延误模型：延误模型一（恢复通车后延误影响结束），延误模型二（恢复通车后延误影响持续）。

1.2.1 延误模型一

线路恢复通车时，若N′≤Nm，则在站台等候的乘客可以自由乘坐到达列车，滞留乘客疏散时间T2＝0，后续到达乘客不再受到影响，该次事故对乘客的延误影响结束。如图1所示。

图1 模型一延误分析图

延误持续时间为

受到延误的乘客包括事发时系统内原有乘客和延误持续时间内到达的乘客，即：

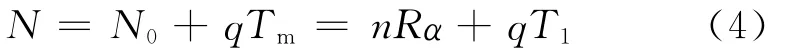
事故造成的乘客延误总时间Ty由原有乘客延误和延误持续时间内到达乘客延误两部分组成，即为图1中阴影部分的面积Sa。

1.2.2 延误模型二

线路恢复通车时，若N′＞Nm，则此时线路进入临时满负荷运行状态，且会有部分乘客（N′－Nm）滞留站台，后续到达乘客也将受到延误影响，事故的延误持续时间范围为线路受阻起至站台不出现乘客滞留为止。如图2所示。

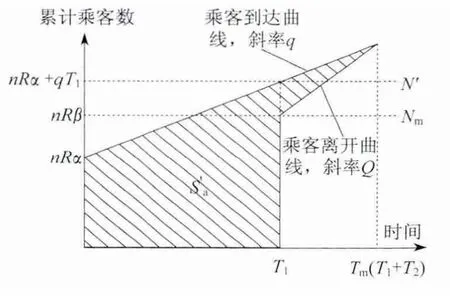
图2 模型二延误分析图

在乘客疏散阶段，线路处于动态饱和状态，乘客得到运输服务的速率等同于乘客离开线路的速率，全线内滞留乘客数量将以Q－q的速率减少。

滞留乘客疏散时间为：

延误持续时间为：

受到延误的乘客包括事发时系统内原有乘客和延误持续时间内达到的乘客，即：

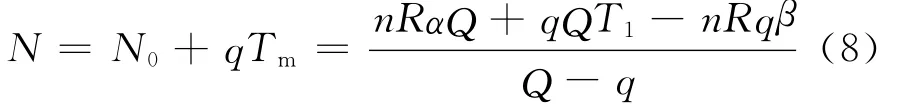
事故造成的乘客延误总时间由原有乘客延误和延误持续时间内到达乘客延误两部分组成，即为图2中阴影部分的面积。

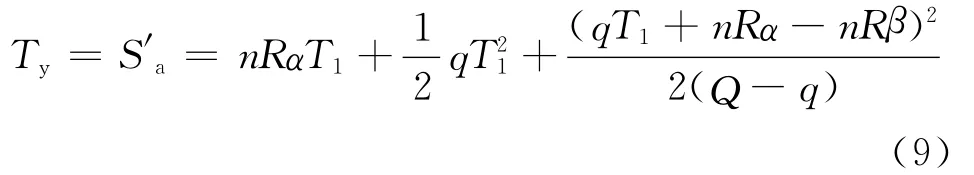
1.3 延误损失模型

地铁事故延误社会损失主要体现为乘客在途时

间增加造成的出行者时间价值损失。个体的时间价值可由其劳动力价值体现。延误损失计算模型为：

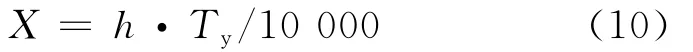
式中：

X——地铁事故社会延误经济损失，万元；

h——人均劳动力价值，元／（人·h）；

Ty——乘客延误总时间，h。

2 计量因素分析

2.1 单位时间劳动力价值

2012年度上海人均国内生产总值（GDP）为73297元。按照中国统计年鉴和投入产出表提供的我国GDP的初次分配情况，近年来我国GDP中劳动者报酬比重保持在45%左右。由于我国的市场经济体制还不够成熟，初次分配的统计数据还不能充分说明劳动力和资本对GDP贡献的实际份额。有学者结合道格拉斯生产函数和回归方法计算得出我国劳动力对GDP的贡献份额在0.58～0.6之间。这表明受到运输影响的社会劳动价值的损失也应以GDP的60%为基础进行估算。据此，可得h＝21.99元／（人·h）。

2.2 高低峰时段客流

图3 工作日客流分布

由图3可看到，客流量呈明显的双峰分布，具有工作日客流量的典型特征。2号线当天客流量包括到站和换乘总计为136.6万人次，其中84.2万人次直接出站，52.4万人次则通过换乘离开2号线。

随机抽取上海轨道交通2号线某工作日客流数据（见图3），运营时间以18h为计。其中，高峰时间约5h，低峰时间约13h。

高峰时段（7：00—10：00，17：00—19：00）内平均客流量为14.60万人次／h，低峰（非高峰）时段内的平均客流量为4.89万人次／h，高峰时段与低峰时段的平均客流量比为3∶1。

当日断面客流量峰值出现在8：45—8：59的15 min内，静安寺—南京西路区间断面客流量达到最多的12941人次，该时段内进、出该线车站的人数分别为4.0万人次和6.6万人次。以发车间隔3min计，15min内有5列列车经过同一断面，经计算，断面客流量最大区间内的列车载客人数可达2588人。但由于客流空间分布不均，即使在高峰时段，近郊区域内的列车载客人数依然较少，致使全线列车平均满载率不高。2号线8：45—8：59断面客流量见表1。

表1 2号线8：45—8：59（15min）断面客流量 人次

依据2号线断面分时客流统计情况，各区间15 min断面客流均值在高、低峰时段分别为3881人次和1421人次，以15min内断面经过5列车计，平均每列车载客数在高、低峰时段分别为776人和284人，以列车定员2480人／列计，其平均满载率分别为31.3%和11.5%。由此可知，地铁客流和列车满载率在高低峰时段差距很大。本文在估算延误损失时，将根据事故发生的时段，采用对应的计量参数数值。

2.3 线路运行车辆

2号线实际上可分为相对独立的2段线路：徐泾东—广兰路与广兰路—浦东国际机场。2段线路采用不同的列车编组，由于广兰路—浦东国际机场客流不到2号线总客流的10%，故本文不再另行分析。

2号线徐泾东—广兰路段采用A型车8节编组，定员2480人／列，全线共有列车53列，除去检修和备用的车辆，正线运营列车可以保持在40列左右。本文的线路运营列车数以40列计。

由于客流在空间上的分布是不均匀的，当部分区间列车载客饱和时，其他区间内的列车仍有大量剩余运能，在计算整条线路列车的载运能力时，对此应加以考虑。2号线在8：45－8：59时间内断面流量达到最大，线路满负荷运行。该时段内的各区间断面流量均值为7294人，全线列车平均载客数为1459人／列，以此作为单列列车的最大载客能力，则线路满负荷时的列车平均满载率为1459／2480×100%＝58.8%，β取值为0.588。

2.4 延误模型选择

当事故发生时，根据其所处的时段，可以确定当时的列车满载率和进入线路内的客流，线路恢复通车时系统内的乘客总数取决于恢复通车的时间。记恢复通车时间临界值为T1′，两种延误模型的边界条件为N′＝Nm，由nRα＋T1′q＝nRβ得：

当T1≤T1′时，选择延误模型一；当T1＞T1′时，选择延误模型二。

线路高低峰时段内的客流情况差别较大，应分开讨论。

2.4.1 低峰时段延误模型

当事故发生在低峰时段时，进入线路内的客流取低峰时段客流均值q＝4.89万人次／h，列车满载率取低峰时段列车满载率均值，α＝11.5%，n＝40列，R＝2480人／列，β＝0.588。将参数代入式

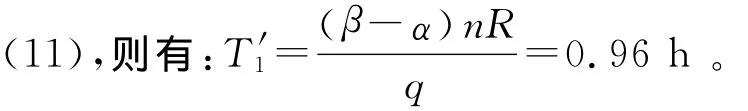
低峰时段恢复通车时间在0.96 h（58 min）内的事故，应选用延误模型一计算延误损失。

根据地铁事故统计，大部分事故造成的列车最大晚点在15～30 min内，极少有延误超过58 min的。在2号线近几年的事故统计中，未出现过延误超过58 min的事故。因此，凡发生在低峰时段的事故，计算其延误经济损失时，均可采用延误模型一。

2.4.2 高峰时段延误模型

当事故发生在高峰时段时，进入线路内的客流取高峰时段客流均值q＝14.60万人次／h，列车满载率取高峰时段列车满载率均值，α＝31.3%，n＝40列，R＝2480人／列，β＝0.588。将参数代入式

高峰时段恢复通车时间超过0.19 h（12 min）的事故，应选用延误模型二计算延误损失。

根据上海申通地铁集团有限公司的事故分类标准，因设备故障、操作不当、管理不善等致运营列车延误15 min以上，视为一般E类事故纳入事故统计。在有统计的事故中，对运营造成延误影响的，其最大晚点均超过12 min，可以认为，凡是发生在高峰时段的事故，计算其延误经济损失时，均可采用延误模型二。

3 地铁事故延误损失估算

3.1 实例计算

假设2号线某路段9：00发生事故，造成线路最大晚点21min，计算该事故造成的延误经济损失如下：

（1）确定计量参数。该事故发生在高峰时段，取q＝14.60万人次／h，T1＝21min（0.35h），α＝31.3%，β＝0.588，满负荷时离开线路的客流Q＝26.4万人次／h，R＝2480人／列，n＝40列，h＝22元／h。

（2）延误总时间计算。事故发生时段为高峰时段，采用延误模型二。将计量参数代入式（9），可得乘客延误总时间为：

将计量参数代入式（10），可得延误经济损失为：

X ＝h×Ty／10000＝48.9万元

3.2 年度事故延误损失

2012年度上海轨道交通2号线事故统计中，造成列车延误的事故有10起，其中2起发生在高峰时段，各事故的最大晚点时间均在15～30min范围内。年度延误事故统计及社会延误经济损失估算如表2所示。

由表2可知，2012年度，2号线10起的事故共造成乘客延误12.6万h，延误经济损失277.9万元。虽然延误持续时间相同，但高峰时段的事故延误经济损失比低峰时段的大得多，通常为3～4倍；高峰时段发生的事故虽然只有2起，但其延误经济损失为131.3万元，占总延误损失的近半数。在制定事故防范措施和处理流程时，应特别注意减少高峰时段事故的发生频率和处理时间。

表2 年度事故延误社会经济损失汇总

4 结语

地铁事故社会经济损失评价是交通安全经济分析的重要内容，也是地铁安全管理和事故防范决策的重要依据。本文从地铁事故损失的基本理论、评估方法、量化指标等方面进行分析，并根据地铁客流的时段分布特征建立了适用于高低峰时段的延误模型。在整理上海轨道交通2号线2012年度统计事故情况的基础上，通过延误模型的应用，计算出该年度2号线事故延误经济损失，并得到高峰时段单次事故延误损失远大于低峰时段的结论。

［1］周淮.上海轨道交通运营客流简析［J］.地下工程与隧道，2005（4）：1.

［2］姜晓明，荆新轩，顾保南，等.上海市轨道交通换乘现状的分析与对策［J］.城市轨道交通研究，2003（4）：36.

［3］罗云.安全经济学导论［M］.北京：经济科学出版社，1993.

［4］吴慈生.人－机－环境系统的安全价值分析［J］.中国安全科学学报，1993（增刊），411.

［5］姜华平.道路交通事故社会经济损失评价理论研究［D］.长春：吉林大学，2005.

［6］张鲁喻.铁路运输安全投资经济效益的初步分析［D］.北京：北京交通大学，2008.

［7］程国斐.国民收入初次分配中劳动者报酬份额的演变规律和地区差异［D］.青岛：山东大学，2013.