某露天矿排土场边坡稳定性分析

张鲲华，陈玉明，张绍周

（昆明理工大学国土资源工程学院，云南 昆明 650093）

【其 他】

某露天矿排土场边坡稳定性分析

张鲲华，陈玉明，张绍周

（昆明理工大学国土资源工程学院，云南 昆明 650093）

排土场边坡稳定性问题成为阻碍我国露天矿发展的重大因素而得到国家和社会的广泛重视。本文总结排土场的发展趋势，结合某露天矿排土场的工勘地质特征，采用极限平衡法和FLAC3D强度折减法对排土场稳定性进行计算，计算结果相差不超过0.04，计算结果显示FLAC3D强度折减法计算安全系数具有很好的可靠性，计算不收敛判据与塑性贯通判据在本例中等效。安全系数平均值为0.480，反分析排土料的物理力学参数，认为达不到稳定要求的强度，故认为该排土场存在重大安全隐患，应及时治理。通过数值模拟研究边坡的失稳机制对于边坡稳定将有更为积极的意义。实践过程中，应当重视计算参数获取的准确性。

排土场；边坡稳定性；极限平衡法；FLAC3D强度折减法

1 概述

露天开采在采掘工业中占有举足轻重的地位。据估计，世界上矿产资源的露天开采比重已经超过2/3。我国铁矿石露天开采产量占总产量的86%～91%，有色金属矿露天开采产量占总产量的46%～49%[1]。露天矿边坡工程是一项关系矿山安全生产、矿山可持续发展和取得矿业开发重大盈利效益的关键课题[2]。随着露天矿开采进入中后期，露天矿排土场滑坡呈递增趋势，排土场滑坡不仅影响到矿山自身的安全生产，还会造成重大人员伤亡和环境破坏，并产生重大的经济损失和严重的社会影响[3]。

我国冶金矿山90%属于露天开采，每年剥离的岩土量约4亿t，占地10km2，其他有色金属矿每年排弃的岩土约0.5亿t，全国煤矿排弃的煤矸石每年约1亿t，露天排土场占地面积约为全矿的30%～50%[4]。随着边坡稳定性评价的发展，排土场的排土潜力得以较大的挖掘，以排土场增容研究为题的研究成果不断涌现，改进排土工艺为排土场的增容实现提供重要保证。基于节约用地和稳定性的排土场优化设计将成为排土场发展的必然趋势。

2 某露天矿排土场工程概况

2.1 水文地质

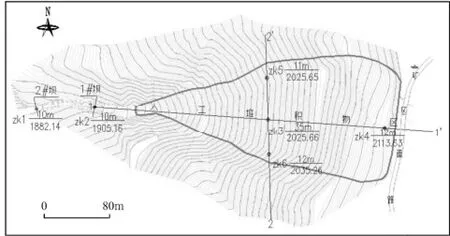
图1 勘查区平面图

工程区位于红河水系左岸，由于区内大部分为碳酸盐岩分布，溶洞、溶隙发育，花岗岩出露区风化强烈，节理裂隙，虽然降雨量充沛，但由于大气降雨后多以垂直入渗的方式渗入地下，形成地下径流，从ZK1～ZK6(图1)反应出勘察区浅层无地下水位，雨季仅有部分形成地表径流，向南西汇入红河。地下水类型主要以裸露型岩溶水为主，其次为碎屑岩风化裂隙水、第四系为松散层孔隙水。本工程区基岩裸露，以大气降水为地下水主要补给源，含水层大面积分布于该单元内，岩溶裂隙发育，形成岩溶水径流带，地下水由东向西径流。碎屑岩风化裂隙水中的风化裂隙水埋藏较浅，分布受地形、地貌控制，普遍为潜水性质，风化裂隙的发育程度与岩性、地形、地貌、植被等有密切关系，而且随着深度的增加，风化裂隙逐渐减弱，故一般浅，富集条件差。第四系松散层孔隙水含水层岩性单一，孔隙水分布零星，分散，富水性不均一，盆(谷)地内地下水接受大气降水、地表水的补给，由于地势平坦，水力坡度小，富水性和渗透性较差，降雨后多形成地表径流，向附近低凹处排泄，具有就地补给就地排泄的特点。

2.2 地形地质

边坡区属构造侵蚀中低山—低山区，为卡房断裂中等切割河谷地貌，地势陡峻，地形坡度26～50°，岩石风化强烈，裂隙发育，雨水对边坡不断冲刷，降低了边坡的安全等级，并且加速了边坡的滑坡和崩塌速度。

根据地面工程地质测绘和钻探揭露，治理区主要出露地层为中生界三叠系灰岩、印支期花岗岩、残坡积层及人工堆积物。中生界三叠系灰岩：上部厚度约4m为浅灰、青灰色，中—厚状的强—弱风化石灰岩，溶洞和溶隙发育，是地表水的渗漏通道；4m以下为微—未风化石灰岩，青灰色，中—厚状，结构致密，脆性大，强度高。印支期花岗岩：强风化花岗岩，灰白色，风化裂隙发育，易碎；弱风化花岗岩，灰白色，结构致密，硬度高，强度大。残坡积层：碎石土为浅黄、暗红色块石夹粉土，松散，块石形态不规则，棱角明显，混杂堆积，以石灰岩、花岗岩强风化碎块为主，块石粒径100～300mm，粗砾含量40%～60%。人工堆积物(碎石土)：浅黄、暗红色块石夹粉土，松散，块石形态不规则，棱角明显，混杂堆积，以花岗岩强风化碎块为主。

2.3 物理力学性质

采用不同深度钻孔岩心做直剪试验测定排土的物理力学参数如表1。

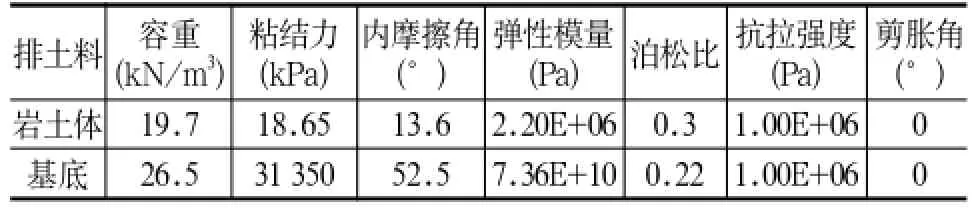
表1 直剪试验测定排土料的物理力学参数

2.4 地震

工程区附近较为活跃的断裂是小江断裂，该断裂属壳断裂，活动时代Q3-4，活动方式左行走滑，速率1.0～8.6mm/a，北强南弱，发生5.0～5.9级地震18次，6.0～6.9级地震9次，≥7.0级地震4次，最大地震8级。

3 稳定性分析

3.1 方法选取

(1) 极限平衡法。

极限平衡法是边坡稳定性分析计算的主要方法，也是工程实践中运用最多的一种方法。极限平衡法是根据边坡上的滑体或滑体分块的静力平衡原理分析边坡各种破坏模式下的受力状态，以边坡滑体上的抗滑力和下滑力之间的比值来评价边坡的稳定性。在大多数情况下，边坡稳定性问题是静不定的，边坡受力的平衡方程中未知数的个数大于方程个数，为了使方程有唯一解，通常引入假设将静不定转化为静可解，这种处理使解决问题的严密性受到破坏。但由于极限平衡法计算模型简单、计算参数量化准确、计算结果直接适用而被广泛应用。极限平衡法理论体系的发展完善形成了以不同适用范围和假设条件的计算方法，李小春等[5]认为不应指定某一种方法作为验算的唯一方法，可以选择多种精度较高的方法(如M-P、Spencer、Bishop、L-K法)的均值作为验算方法。当条件具备时，应尽量采用满足所有平衡条件的方法，其具有较高的精度与较低的标准差，计算结果稳定可靠。Bishop法具有良好的替代性，计算精度较高。

(2) FLAC3D强度折减方法。

FLAC3D中采用强度折减系数来定义安全系数[6-7]。若边坡采用Mohr-Coulomb准则，影响其稳定性的强度参数粘结力C 和内摩擦角φ，将坡体原始粘结力C0

和内摩擦角φ0同时除以一个折减系数K，然后进行数值分析。通过不断增大K，反复分析直至边坡达到临界破坏状态。假设此时的粘结力和内摩擦角为Ccr和φcr，由于边坡处于临界状态，所对应的安全系数Kcr=1，可得原始边坡所对应的安全系数为：

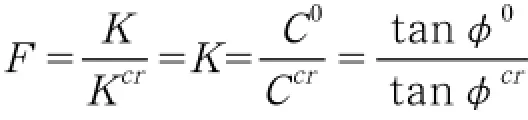
本文采用极限平衡法与有限差分方法相结合计算排土场边坡安全系数，对排土场边坡的稳定性作出合理评价。在有限差分方法中采用计算不收敛判据，破坏之前计算收敛，破坏之后滑面上岩土体无限流动计算不收敛。计算过程中记录最后一个循环最大不平衡力及最后一步塑性贯通状态。

3.2 计算过程

(1) 模型建立。

排土料在山谷中部堆置较厚，山谷两侧堆置变薄。由此认为沿原地形山谷线剖面为排土场存在安全隐患最突出的剖面，以此剖面作为排土场安全系数计算的剖面(如图2)，图2中人工堆积物水平总长度约310m，沿坡向下游堆积，厚度逐渐变厚，坡顶ZK4位置堆积存5.4m，中部ZK3位置堆积厚33.6m，下游边缘距ZK2约50m，堆积物结构松散，易产生滑坡和泥石流，从坡脚向坡顶堆积物粒径逐渐变小，分选明显，其下覆地层为强风化易破碎结构松散花岗岩和强—弱风化石灰岩。

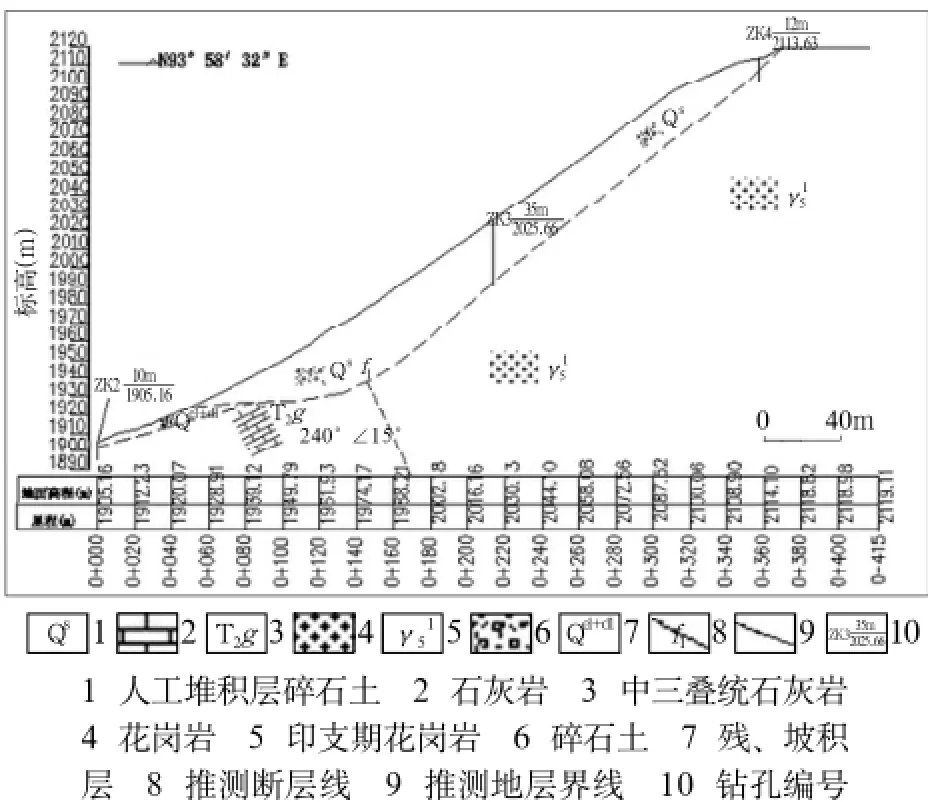
图2 排土场最危险剖面

由于残、坡积层厚度和范围较小，为了计算简化，将其物理力学参数用印支期花岗岩的代替。计算模型既要包括整个潜在滑坡体，又要有一定的外延，尽可能减少边界条件对计算结果的影响。当坡脚到左端边界的距离为坡高的1.5倍，坡顶到右端边界的距离为坡高的2.5倍，且上下边界总高不低于2倍坡高时，计算精度最为理想[8]。建立如图3的计算模型。

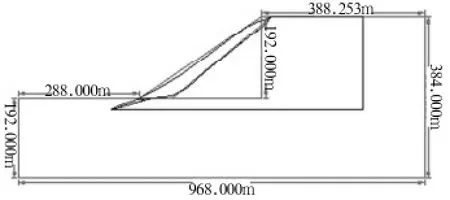
图3 计算模型

(2) 计算结果。

将图3中简化的计算模型导入到理正软件中，应用复杂边坡计算模块，输入物理力学参数和控制参数计算排土场边坡的安全系数。假设滑坡为圆弧形，采用通用方法自动搜索最危险滑裂面，土条宽0.5m，搜索时的圆心步长和半径步长都为5m。土柱位置误差为1m。

图4 FLAC3D计算模型

在FLAC3D软件中建立如图4的计算模型，自编强度折减程序计算排土场边坡的安全系数。折减过程只对排土料进行。模型建立了45 312个单元共57 970个节点的有限差分网格，采用Mohr-Coulomb模型并赋相应材料参数，模型受重力影响，不考虑孔隙水压，模型四周和底面固定。通过试算，模型在计算30 000步以内已经达到平衡状态，同时将计算最大不平衡力与典型内力的比率不超过1.0e-5为收敛准则，计算精度设置为0.001，计算结果如图5、图6和图7所示。

(3) 计算结果分析。

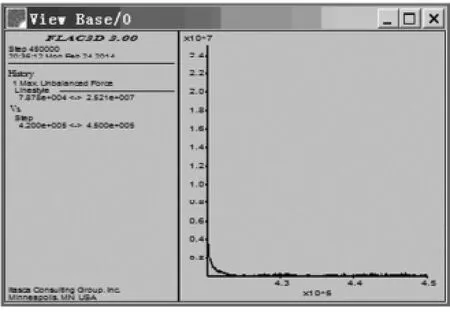
图5 最大不平衡力

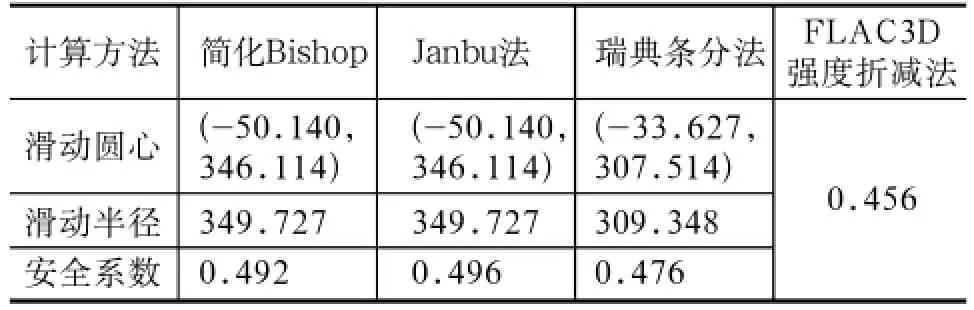
表2 安全系数计算结果

安全系数计算结果见表2，由表2可以看出，排土场边坡安全系数都小于1，排土场边坡已经破坏，实地踏勘排土场边坡现状并未出现坡体拉伸破坏。可能存在如下原因：①取样岩心的级配组成与排土场的实际的级配组成不一致。取样岩心来自ZK3和ZK4，取了6组样进行直剪试验；②直剪试验存在缺陷，剪切面限定在上下盒之间的平面，而不是沿土样最薄弱的面剪切破坏。剪切面上的剪应力分布不均匀，且竖向荷载会发生偏转，主应力的大小和方向都是变化的，对试验结果产生影响；③粘性土具有触变性，其强度会因为受到扰动而削弱。在运输过程中，岩土体的结构可能因为震动发生改变。

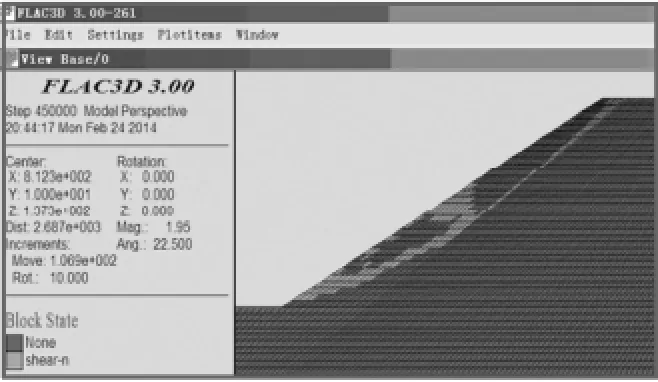
图6 塑性贯通区

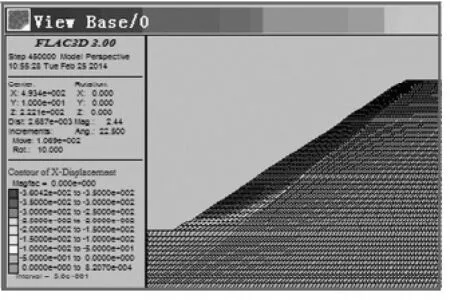
图7 X 方向的位移云图

虽然岩土体的物理力学参数存在一定的误差，但是采用不同计算方法计算的安全系数之间差别不大，最大值与最小值之间相差为0.04，由此证明计算的正确，该排土场边坡稳定性系数为0.480。排土场边坡计算过程未考虑孔隙水压及地震的影响，孔隙水压和地震因素都是降低边坡稳定性的因素，即使试验得到的岩土体物理力学参数偏小，不考虑孔隙水压和地震将使计算结果误差减小。另外，当排土场边坡达到临界状态时，需要材料的粘结力为40.899kPa和内摩擦角为27.937°，砾砂、角砾和粉质粘土是在天然状态下难以达到此强度[9]。所以排土场边坡存在重大安全隐患，应当及时采取治理滑坡措施。

4 结论

工程案例安全系数计算说明FLAC3D强度折减系数法具有很好的可靠性。FLAC3D强度折减不需要假设危险滑移面形状，采用计算不收敛作为边坡破坏判据是可行的。边坡滑动失稳是在内外综合因素的作用下，系统从量变到质变，从劣化因素的不断积累到最终发生突变失稳的一个变化过程[10]，通过数值模拟研究边坡的失稳机制对于边坡稳定将有更为积极的意义。考察FLAC3D计算的最大不平衡力(图5)、塑性区贯通状况(图6)和X方向的位移云图(图7)，图5显示最大不平衡力是收敛的，模型在30 000步内能达到平衡状态。图6显示在计算不收敛判据成立条件下塑性区贯通仍然成立，说明这两个判据在判断边坡破坏时具有相同效应。图7显示边坡的破坏为圆弧形(X方向位移为0)，由此证明在极限平衡法中的假设成立。

在计算过程中，参数的准确与否将决定计算结果的可靠性。在生产实践中，应当重视岩土体物理力学参数的获取，采取有效措施减小参数误差。

[1]梁克钧.国内外露天采矿技术水平与动向[J].河北矿冶学院学报，1983(1)：45-59.

[2]张四维.我国露天矿边坡工程研究成果与进展[J].地质灾害与环境保护，2000，11(2)：98-101.

[3]孙世国，杨宏.典型排土场边坡稳定性控制技术[M].北京：冶金工业出版社，2011.

[4]薄建芬，候豆豆.露天矿山排土场安全管理措施研究与应用[C]∥鲁冀晋琼粤川辽七省金属(冶金)学会第十九届矿山学术交流会，2009：982-988.

[5]李小春，任伟，王少泉，等.论金属矿山排土场设计规范中边坡极限平衡计算方法的选取[J].岩石力学与工程学报，2011，30(Z2)：4136-4142.

[6]赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报，2002，24(3)：343-346.

[7]张鲁渝，郑颖人，赵尚毅，等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报，2003，34(1)：21-27.

[8]郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报，2004，23(19)：3381-3388.

[9]林宗元.岩土工程勘察设计手册[M].沈阳：辽宁科学技术出版社，1996.

[10]孙书伟，林杭，任连伟.FLAC3D在岩土工程中的应用[M].北京：中国水利水电出版社，2011.

TD824.71；TD824.8

A

1007-9386(2014)05-0059-04

2014-02-28