基于小波变换和QNN的TRT中透平机运行状况预测*
马 亮 ,杨萍萍 ,龚雨含
(1.河北联合大学 轻工学院,河北 唐山 063000;2.河北联合大学 电气工程学院,河北 唐山 063000)
TRT系统中的透平机作为一种旋转机械,是高炉煤气余压发电设备中的重要组成部分,它的正常运转可以保证稳定高炉炉顶压力,降低炉况的变化范围,使高炉更易取得高效的产出,其结构复杂,故障特征的表现及故障的产生原因普遍具有模糊性和复杂性,对其进行潜伏性故障诊断存在一定的困难[1-5]。针对以上问题,国内外在此方面已经进行了一定的研究,但是与其在生产中广泛应用的现状不相符合。
针对以上情况,本文在对高炉煤气余压发电技术做深入了解的基础上,选择此技术中的关键设备透平机作为研究对象,针对其存在旋转机械的特点,通过理论分析,首先应用小波变换的方法[6-7]将透平机运行状况相关数据中的噪声滤除,然后通过分析透平机运行过程中相关环节的关系,在现场采集到的大量数据信息积累的基础上,采用量子神经网络实现对TRT系统中透平机运行状况的潜伏性故障诊断。
1 透平机运行数据的预处理
由于TRT机组的工作现场环境复杂,透平机的运行受到电磁及地面振动等诸多因素的影响,从传感器获得的信号中不可避免地混有大量的噪声干扰,这对正确预测透平机的运行状况非常不利。因此,首先需要对从现场采集到的透平机运行数据进行滤波处理。
在仿真实验中,首先确定阈值,由于Donoho给出的通用阈值计算方法所得出阈值在不同尺度上是相同的,而噪声通过小波变换所产生的小波系数在不同尺度中都是均匀分布的,其幅值伴随尺度的增加不断减少。因此,为了符合噪声在小波变换各个尺度上的传播特性,实验中采用的阈值估计函数为:
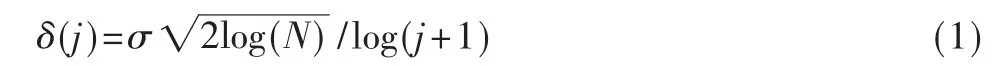
式中,σ为噪声强度,N为信号长度,j为分解尺度。
信噪比是测量信号中噪声量的传统方法,常被用来作为消噪效果评价的指标。实验中采用的信噪比SNR函数为:
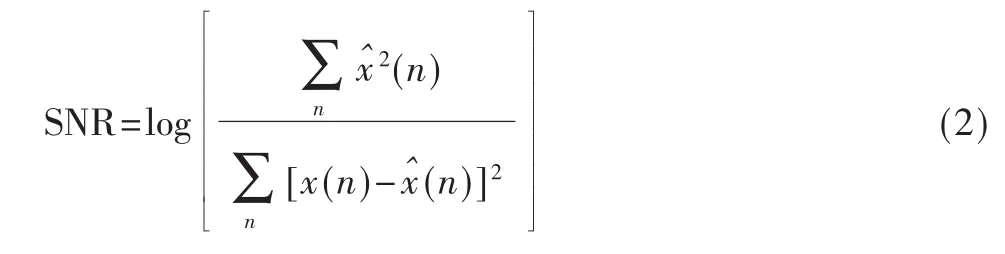
式中,x(n)为原始信号,xˆ(n)为经过小波变换滤波后的估计信号,滤波之后的信噪比越大,滤波的效果越好。
对从现场采集到的透平机位移、转速、振动三组数据中分别选取1 024个采样点。在仿真实验中,采用db5小波基函数进行5层分解,随着小波尺度的增加,噪声干扰逐渐被滤除,信号和噪声基本被分离,再应用软硬阈值折衷算法处理分解后的小波系数,最后做小波逆变换进行信号的重构,滤波前后的信号如图1~图3所示。
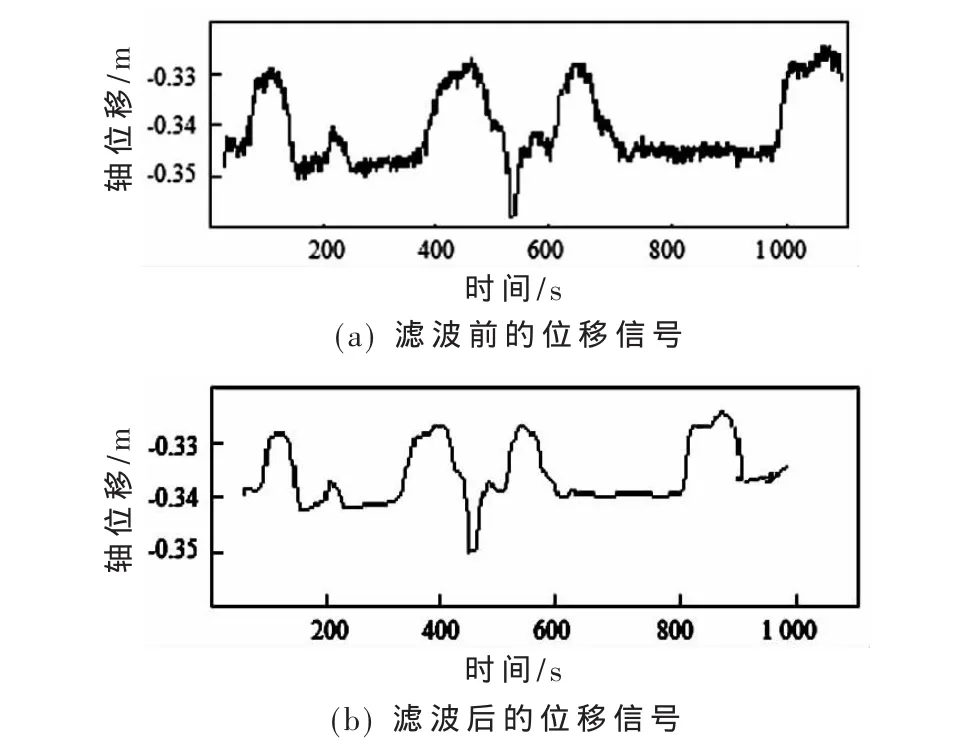
图1 滤波前后的位移信号
比较图1中滤波前后的透平机位移信号可以看出,此算法可以有效地滤除高频、低频的噪声干扰信号,还原原始信号。
通过比较图2中滤波前后的透平机转速信号可以看出,此算法处理信号的局部细节特征有很好的效果。
通过比较图3中用软硬阈值折中算法滤波前后的透平机振动信号可以看出,此算法无论是从滤波效果还是保存有用信号中的尖峰和突变部分都做得非常好。
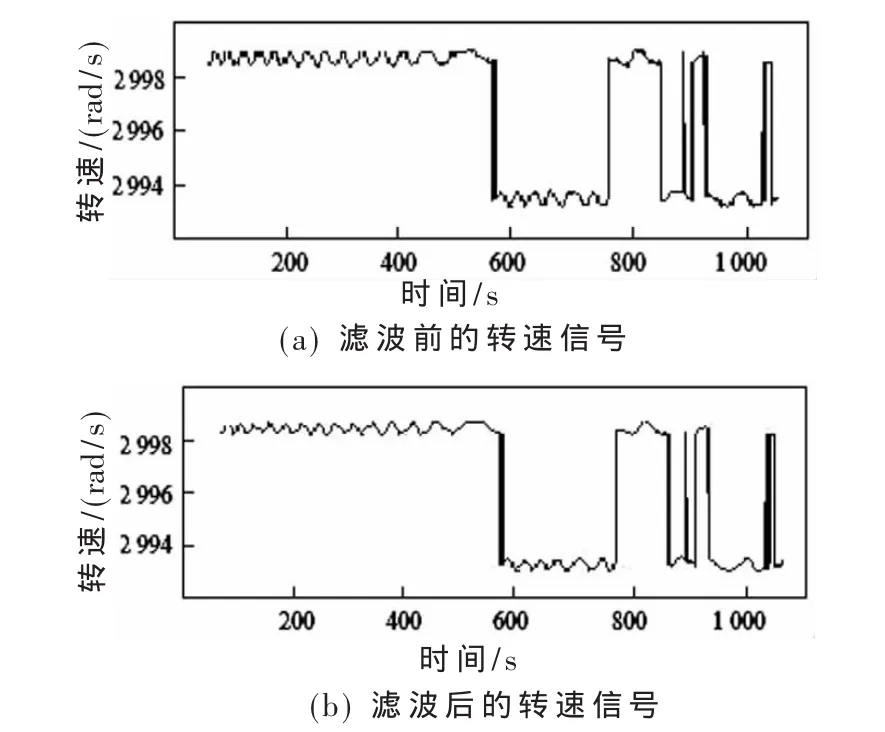
图2 滤波前后的转速信号
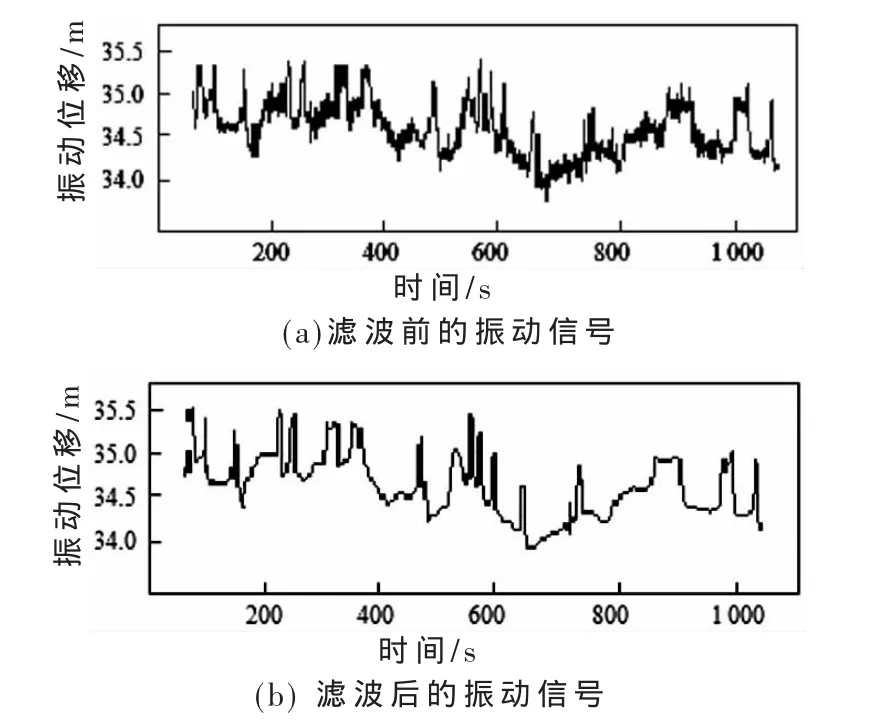
图3 滤波前后的振动信号
通过比较滤波前后的三组透平机运行数据,可以看出滤波后的信号中噪声部分被有效地抑制。同时,滤波后的信号作为随后的透平机运行状况预测的输入数据,可以有效地提高预测的可靠性和准确性。
为了体现软硬阈值折衷法在小波阈值滤波算法中的优势,分别采用软阈值算法、硬阈值算法和软硬阈值折衷法对透平机运行中振动信号的滤波进行了比较实验,实验所得的信噪比和均方差两项指标如表1所示。
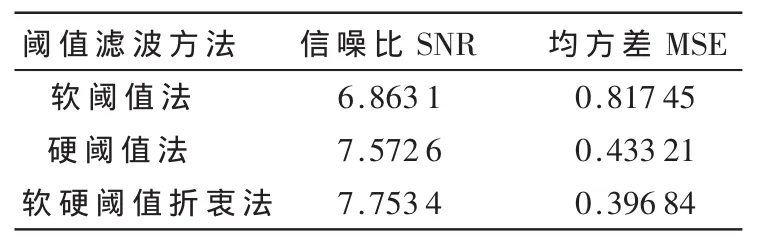
表1 阈值滤波方法比较
从表1中可以看出,软硬阈值折衷法的滤波性能在信噪比和均方差上都要优于另外两种算法,此方法不仅能够避免硬阈值函数的不连续性,并且能够去除软阈值函数在小波系数的分解过程中产生的差值,是一种更加有效的滤波算法。
2 透平机前轴瓦温度的预测
选取在透平机运行时对轴瓦温度影响较大的7个运行参数(透平机的轴位移、进气侧X向振动、进气侧Y向振动、进气压力、润滑油压力、润滑油温度、转速)作为输入层节点。隐层神经元节点数的选取没有明确的规定,但是隐层节点太少,不能反映后续值与前驱值的相互关系,容错性差;隐层节点太多会导致学习时间过长,网络预测能力下降。本文采用经验公式与试凑法相结合的方法来确定隐层节点个数,经验公式选取和n2=log2m,式中,n1为隐层节点数,m为输入层节点数,p为输出层节点数,a为[0,10]之间的常数,激活函数选用对数函数σ=1/(1+e-t),网络的初始权值由随机函数给出,在带动量的BP算法中,取容许的最大误差率为er=0.01,动量因子常数 mc=0.97,初始学习速率 lr=0.8,学习速率减少率dm=0.9,学习速率增长率im=0.92,陡度因子αn=0.94,量子间隔数目ns=3,网络的训练误差SSE=10-3,最后将量子神经网络采用预处理后的数据进行训练,对网络输出的数值应用反变换即可获取实际的预测值[8-10]。
研究人员通过理论的分析已经证明,含有单个隐含层的神经网络能够模拟任何连续函数,仅当神经网络的学习存在不连续的问题时,才需要设计出两个隐含层。实践结果显示,如果存在一个隐含层的节点数添加了很多,却仍然不能使网络的性能有所提高的情况,可以通过选取两个隐含层,并且适当减少隐含层节点数的方法提高神经网络的性能。因此,在量子神经网络隐含层的选取上,可使用具有一个或者两个隐含层的网络模型结构,并比较两者的训练性能上的差别。本文以选取两个隐含层为例,分别含有24和18节点的网络结构,得到预测结果以及训练曲线,如图4和图5所示。
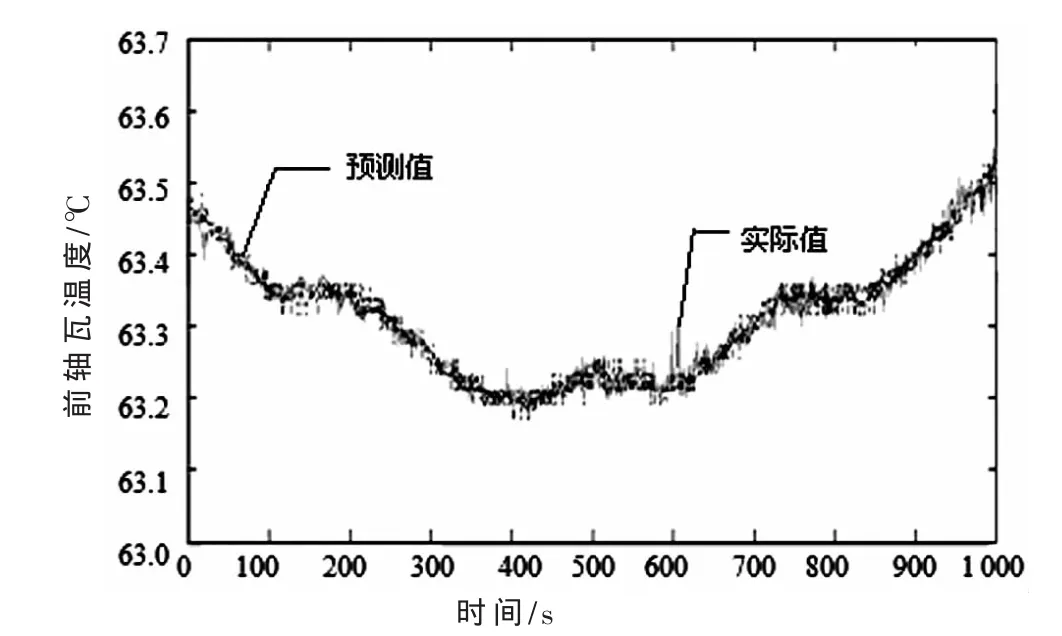
图4 预测曲线
通过图4可以看出,预测曲线能很好地逼近实际曲线,尤其在运行中状态突变的时刻预测效果非常明显,此量子神经网络对透平机前轴瓦温度的预测能够得到满意的结果。
通过图5可以看到,在经过 195次训练后,所建立的神经网络到达了目标精度,相对误差为0.54%。
通过表2的比较可以看出,量子神经网络模型选取7-24-18-1的结构,无论是在网络训练的速度还是在减少泛化误差上都做得最好。选择三层的7-24-1网络结构,尽管在提高目标精度的前提下,仍然具有较快的训练速度,但是泛化误差却增大了。通过比较以上数据,可以得到以下结论:
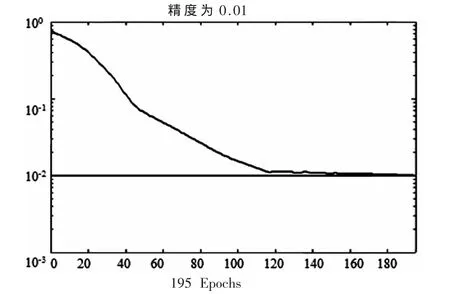
图5 训练曲线
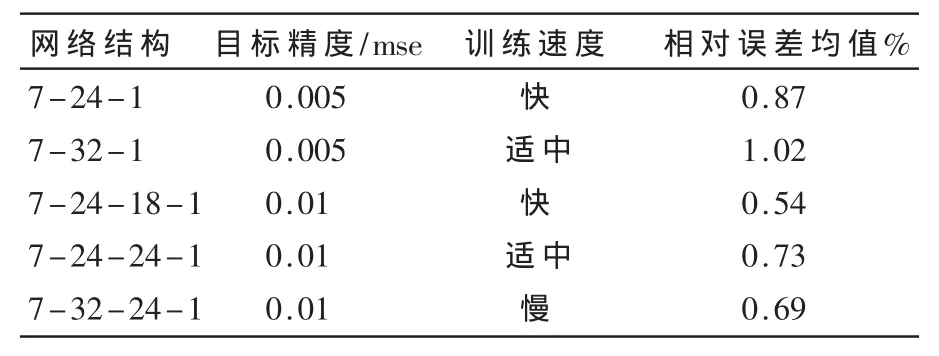
表2 网络结构比较
(1)量子神经网络模型能够实现对TRT系统中透平机运行状况的预测。
(2)对网络结构的选择很重要,尽管具有两个隐含层的网络达到的目标精度较低,但是其泛化误差更小,更合适对新的样本进行预测。
(3)网络的训练精度不能选取得过高,否则在降低网络训练速度的同时,网络的泛化能力也有所下降。
本文针对含有噪声的TRT系统中透平机运行的振动信号运用小波变换阈值化方法中的软硬阈值折衷算法进行滤波处理,能够克服软阈值算法和硬阈值算法各自的不足之处,取得较为理想的滤波效果。通过基于量子神经网络的TRT系统中透平机前轴瓦温度的预测研究可以看出,量子神经网络对TRT系统中透平机运行状况的预测应用是可行的。同时,量子神经网络通过不断地训练和自学习,可以从透平机运行的历史数据中掌握一定的规律,并可以参照这些规律对未来透平机的运行状况做出合理的预测。
[1]王晓放,申岩,黄钟岳,等.通用化透平压缩机运行性能高速在线评估系统设计[J].大连理工大学学报,2005,45(1):36-38.
[2]冯志鹏,宋希庚,薛冬新,等.旋转机械振动故障诊断理论与技术进展综述[J].振动与冲击,2001,20(4):36-40.
[3]冯志鹏,宋希庚,薛冬新.基于广义回归神经网络的时间序列预测研究[J].振动、测试与诊断,2003,23(2):105-109.
[4]王维民,高金吉,江志农.基于有限元模型的旋转机械故障诊断方法研究[J].振动与冲击,2006,25(4):30-33.
[5]宋涛,汤宝平,李锋.基于流形学习和K-最近邻分类器的旋转机械故障诊断方法[J].振动与冲击,2013,32(5):149-153.
[6]臧玉萍,张德江,王维正.基于小波变换技术的发动机异响故障诊断[J].机械工程学报,2009,45(6):239-245.
[7]卢艳宏,冯源.基于小波变换和TMS320F2812的水泵故障诊断系统研究[J].计算机测量与控制,2012,20(10):2642-2644.
[8]李盼池,宋考平,杨二龙.基于受控旋转门的量子神经网络模型算法及应用[J].控制与决策,2011,26(6):888-901.
[9]徐小力,左云波,吴国新.量子神经网络在旋转机组状态趋势预测中的应用[J].机械强度,2010,32(4):526-530.
[10]龚瑞昆,马亮,赵延军,等.基于量子神经网络信息融合的变压器故障诊断[J].电力系统保护与控制,2011,39(23):79-88.

