基于改进模糊层次分析法的复杂装备可靠性分配研究

方明

（天津大学 管理与经济学部，天津 300072）

可靠性分配是根据任务设计书中规定的可靠性指标按照一定的法则从上到下分配给组成系统的分系统、子系统或元器件。传统的分配方法中比例分配法、AGREE法[1-2]只能针对串联系统；另外一些方法如根据复杂度和重要度的分配方法在可靠性影响因素的考虑上不够全面；遗传算法在大规模求解上容易陷入局部最优[3]，拉格朗日乘子法、动态规划法、直接寻查法等在系统级数较大的情况下需要大量的假设和简化，同时存在计算量大、难以获取全局最优解等问题[4]。对于复杂系统的可靠性分配问题，应用传统的方法，很难准确、科学地进行可靠性分配。

层次分析法是20世纪70年代初美国著名运筹学、家匹兹堡大学教授Saaty提出的一种定性分析与定量分析相结合的系统分析方法。之前经典的层次分析法存在以下缺陷：判断矩阵标度采用九标度，在实际操作中由于专家的主观因素占主导地位使得评判结果容易带有片面性；在进行矩阵一致性检验时，如果判断矩阵不具有一致性则需重新构造、计算，直到通过为止，计算量大且精度不高。又由于可靠性分配是在设计的初期阶段进行的，没有大量的数据可供采用，存在很多不确定因素，难以定量进行描述，上述方法不能解决模糊因素带来的问题。因此，在产品设计初期，在实践中应综合考虑以上各种方法的应用，以寻求一种适合于系统自身的复杂性、层次等特点的可靠性指标分配的方法。

1 改进的模糊层次分析法

为了解决传统层次分析法中存在的问题，特采用一种改进的模糊层次分析法[5-8]进行处理。该方法通过采用三标度来判断矩阵标度，使得专家很容易对两两因素做出谁相对重要的决策；而且由优先判断矩阵改造而成的模糊一致性矩阵满足一致性条件，无需再进行一致性检验，也可大大减少迭代次数提高收敛速度满足计算精度的要求；在准则层向对象层进行层次展开时采用隶属度矩阵和模糊加权变换法，充分考虑到各种因素的共同作用，真正体现了综合性[9]；导出了串联系统和并联系统的可靠性分配的一般公式，解决了以往只解决串联系统可靠性分配的问题。

其具体步骤如下：

1）利用三标度法建立互补型模糊判断矩阵P（称其为优先判断矩阵）：

其中，甲表示第i行对应的指标，乙表示第j列对应的指标，n表示准则层中元素的个数。

2）将模糊判断矩阵F改造为模糊一致性判断矩阵Q。求和，并利用转换公式

求得模糊一致性判断矩阵：Q=（qij）n×n

3）利用行和归一法求权重向量。模糊一致性矩阵每行元素之和（不含自身比较）及不含对角线元素的总和分别为：

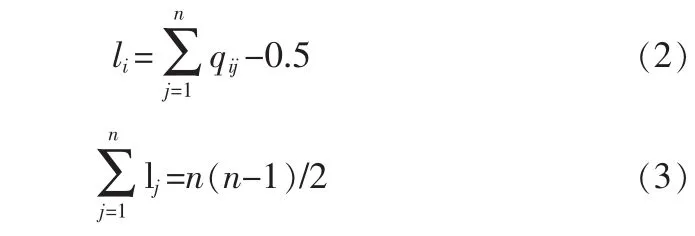
由于表示指标i相对于上层目标的重要性，所以对归一化即可得各指标权重：

所以，农产品质量安全预警能够被定位成：结合预警方式和理论，全面分析和评估反映农产品质量安全的指标，并评判农产品质量风险程度和安全现状以及日后的发展，对农产品质量安全趋势的发展变化进行科学、合理的预测，从而及时拉响警报的过程[2]。

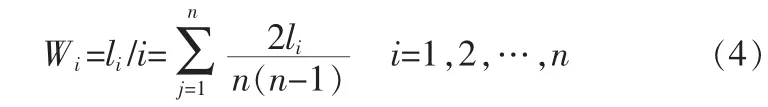
则权重向量为：W=（W1，W2，…，Wn）

4）确定隶属度矩阵。对准则层各个因素，将对象层进行两两分析比较，分别确定出对象层各对象可靠性指标所占的比重pkl和plk（pkl+plk=1），得到关于影响因素的各对象可靠性指标所占比重的模糊关系矩阵:

最小法是确定隶属度矩阵的一种保守取法，取可靠性指标比重的最小值为隶属度矩阵，是常用的工程近似算法。

5）利用模糊变换加权平均法得到评判结果。已知原象W（影响因素权重系数行列式）和映射 （影响因素的隶属度矩阵），利用模糊变换得像（可靠性综合评判的结果）。

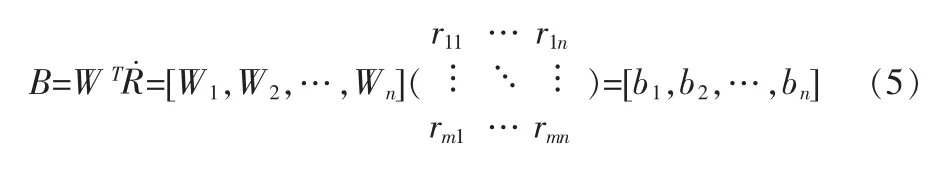
其中b1，b2，…，bn之间的比例关系表示了对象层各元素之间可靠性水平的相对比重；n表示对象层由n个元素组成；m表示m个模糊影响因素。假定各分系统的可靠性指标分别为 R1，R2，…，Rn。 根据上式，有：

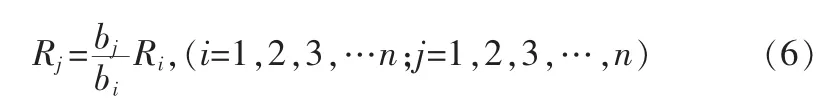
假定系统的可靠性指标为Rs，若以R1为基准

对于串联系统，则有

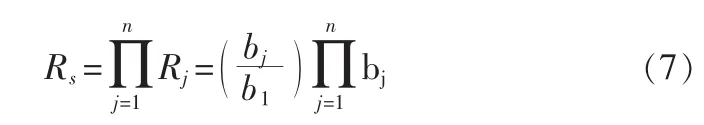
对于并联系统，则有

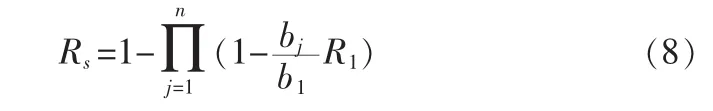
据此式可以求得R1，代入式（6）可求得可靠性指标 R=[R1，R2，…，Rn]。

2 传动链系统的层次结构体系

传动链系统是一个混联系统，为简化计算，把混联系统中的并联部分简化后作为串联系统处理，它由主轴、主轴承、齿轮箱、联轴器、发电机、刹车系统等部分组成。

在对传动链系统进行可靠性分配时，要分别确定出各单元的权重。一般考虑以下几个方面的影响：①单元的复杂程度；②单元的重要程度；③单元的工作环境恶劣程度；④单元的维修难易性；⑤单元的技术水平高低程度；⑥单元的成本改进的高低等。

因此以传动链系统的整体可靠度为目标层E，以影响系统可靠性分配的复杂程度重要程度、工作环境恶劣程度、维修的难易性技术水平和成本造价等6个因素为准则层B，以主轴、主轴承、齿轮箱、联轴器、发电机、刹车系统为对象层建立层次分析模型，制定能够满足电主轴整体可靠度要求的可靠性分配方案，其层次结构模型如图1所示。

图1 传动链系统层次分析结构模型Fig.1 Transmission chain structuremodel of system level analysis

3 传动链系统的可靠度分配

根据层次结构模型和模糊三标度的优先关系，比较准则层的各个因素对整体可靠性分配的影响程度，根据专家评定指导结果，整理得出影响传动链可靠性情况的权重关系：重要程度＞技术水平＞结构复杂程度＞维修难易性＞工作环境＞成本造价。转换成优先关系矩阵如表2所示。

表1 E-B优先关系矩阵Tab.1 E-B preference relation matrix

根据表2中的数据，求行和得：

由式（1），可将表1的优先关系矩阵转化成模糊一致性矩阵：

利用式（2）、（3）、（4）计算出准则层相对于目标层的权重：

根据专家评定结果，整理得出 pi（i=1，2，…，6）为：

用最小值法得到模糊因素的隶属函数矩阵

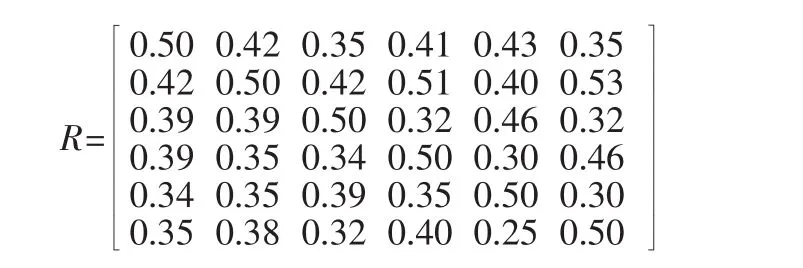
进行模糊变换得到=[0.391 0，0.389 6，0.393 4，0.392 4，0.394 9，0.392 9]

当传动链系统要求的系统可靠性指标为0.95时，利用式6和式7得出各个分系统的可靠性分配指标为R=（0.988 1，0.984 6，0.994 2，0.991 7，0.997 9，0.992 9）

则满足设计要求

一般情况下 0＜Ri＜ 1 （i=1， 2，…，n），如果在某一个系统可靠度指标条件下出现部分分系统可刹车系统靠度分配值大于1，说明该系统的总体设计思想还满足不了可靠性的要求，必须改进在不同影响因素条件下的各分系统可靠性指标所占比重的模糊关系矩阵 pi（i=1，2，…，m），然后重新进行系统可靠性指标分配。同时在处理中为简化计算，是按照串联系统进行分配，在设计实践中，可以将混联系统经过一定方法适当简化为串并联系统，然后按照公式（6）～（8）进行处理。

4 结 论

模糊层次分析法充分利用了对系统可靠性指标分配有重要影响的模糊因素信息，利用人脑对模糊现象做出正确判断，充分发挥了专家的作用，尽量减少了个人主观臆断带来的弊端，是适用于系统可靠性指标分配的科学合理的方法。

为了分析问题的简便，本文把传动链系统看成是由主轴、齿轮箱等单元组成的串联系统，并仅考虑了影响可靠性分配的6个因素，从算法上看是可行的，与实际运行中传动链零部件失效的情况大致吻合，但还有一定的差距。如何将各种不确定因素都考虑进去并进行定量评价，使构建的模型和系统更可靠实用更符合实际情况是今后值得研究的一个问题。

[1]梅启智，廖生，孙惠中.系统可靠性工程基础[M].北京:科学出版社，2002.

[2]郭波，武小悦.系统可靠性分析[M].长沙:国防科技大学出版社，2002.

[3]李峰，刘顺利，陈兵，等.基于遗传算法系统可靠性分配优化模型[J].装备指挥技术学院学报，2004，15（4）:982100.LI Feng，LIU Shun-li，CHEN Bing，et al.System reliability allocation model based on genetic algorithms[J].Journal of Institute of Command and Technology of Equipment，2004，15（4），982100.

[4]张新贵，武小悦.系统可靠性分配的研究进展[J].火力与指挥控制，2012，37（8）：1-4.ZHANG Xin-gui，WU Xiao-yue.Research progress of system reliability allocation[J].Fire and Command Control，2012，37（8）：1-4.

[5]Buckley James J，Feuring T，Hayashi Y.Fuzzy hierarchical analysis [J].IEEE International Conference on Fuzzy Systerms，1999，5（2）:1009-1013.

[6]GU Ying-kui，WU Lu-cheng.A Fuzzy AHP Approach to the Determination of Weights of Evaluation Process[J].China Mechanism Engineering，2007，18（9）:1052-1055，1067.

[7]李永，胡向红，乔箭.改进的模糊层次分析法[J].西北大学学报：自然科学版，2005，2（1）：11-129.LIYong，HU Xiang-hong，QIAO Jian.Improved fuzzy AHP[J].Journal of Northwest University：Natural Science，2005，2（1）：11-12.

[8]宋保维，徐德民.系统可靠性分配的模糊数学方法[J].西北工业大学学报，1998，16（2）:271-275.SONG Bao-wei，XU De-min.System fuzzy reliability allocation method[J].Journal of Northwestern Polytechnical University，1998，16（2）：271-275.

[9]李鸿吉.模糊数学基础及实用算法[M].北京:科学出版社，2005.