基于网络拓扑的动态时延估算模型的研究

豆培培，何泾沙

（北京工业大学 北京 100124）

网络时延测量技术是了解和研究互联网的重要手段。由于在大规模网络中完全实现端到端时延测量非常困难，在测量系统中引入估算可以大大降低主动测量对网络造成的额外负荷，网络时延估算已经成为是网络时延测量技术中重要内容[1]。如何准确地进行网络时延估测已经成为网络测量领域的研究热点，具有重要的研究价值和现实意义。

目前针对时延估算的研究主要包括基于网络结构和基于网络坐标的时延估算技术的研究。IDMaps算法[2]是2001年Francis等人最早提出一种基于网络结构的大规模网络时延估算机制。它以IP地址前缀作为划分AP的标准，采用分布于网络中的若干Tracer估算出Internet中任意两个IP之间的网络距离。2004年Dabek等人首次提出基于网络坐标的分布式的Vivaldi系统[3]，它通过某种嵌入方式将网络空间嵌入到一个度量空间中，这样网络中节点都对应于度量空间中的某个坐标点，然后利用节点坐标计算节点间的空间距离，以此作为节点间的估算时延。但是网络坐标系统存在节点抖动、坐标漂移、链路抖动、三角不等式违例等内在错误。由于网络结构充分考虑了网络的路由拓扑和路径选择等网络内部特性，具有较高的估测精度。然而随着网络规模的不断增大，基于网络拓扑的时延估算系统还有很多需要进一步研究的问题，如提高时延估算精度，优化系统的测量节点部署和提高系统容错性等[4]。文中主要针对基于网络拓扑的时延估算进行了研究。

文中在NS2网络仿真环境中对典型的拓扑结构进行时延测量和分析，得到网络时延与网络拓扑之间的关系，建立了网络时延估算的数学模型。提出了三层时延估测系统架构，可以根据测量节点的测量时延来估算其他端节点到同一目的节点之间的网络时延的算法。最后还给出了完整的动态时延估算算法，可以灵活地根据精度要求直接返回满足要求的时延或者启动自身的测量功能进行测量。

1 仿真设计

本文网络仿真在NS2.35环境中进行，NS2是面向对象的网络模拟工具，具有完备的网络协议，可以仿真整个网络环境，并被广泛使用的强大的开源仿真工具。文献[5]研究表明：互联网平均网络路径长度为15至19跳，国内的平均网络长度为14至15跳之间。我们在仿真实验中设置最大路径长度为15跳。本节主要考虑路径长度与RTT的关系，仿真的网络拓扑示例如图1所示，S0、S1、S2、D0和D是普通节点，中间R1、R2、R3、R4 和 R5是路由器节点。 源节点 S1、S2到目的节点D有两条ICMP数据流。仿真得到节点S1到D，节点S2到D 的两个时延序列分别记为 RTT（S1，D）和 RTT（S2，D）。 其中在S0和D0之间加入基于UDP传输协议的EXPOO背景流量，使仿真更具有动态性。EXPOO是NS2提供的背景流量产生器，它可以根据指数分布（On/Off）产生通信量，在On阶段分组以固定速率发送，Off阶段不发送分组，On/Off的分布符合指数分布，分组尺寸固定。两个数据流的RTT序列如图2所示，可以看出两个时延序列的变化趋势比较一致。

图1 仿真网络拓扑图Fig.1 Topology diagram of the simulation system

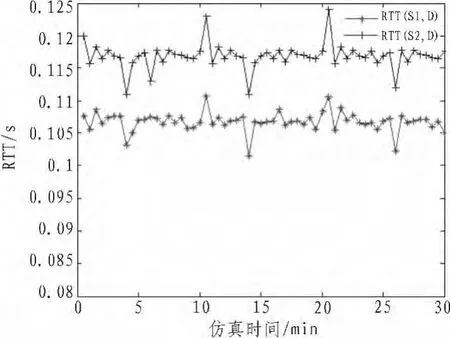
图2 两个RTT序列Fig.2 Two RTT sequenceswith the same destination

2 端到端时延估算的模型

定义1 RTT相似度：网络中两个源节点到同一个目的节点在同一时间段内的两个RTT序列的Pearson相关系数作为S1、S2和D的RTT相似度。

定义2路径长度：定义为源节点到目的节点的跳数，即节点 S1 和 S2 到节点 D 的跳数，分别记作 L（S1，D）和 L（S2，D）。

以图1为例，R2是S1和S2到D的通过的第一个公共路由器，称 L（S1，R2）、L（S1，R2）是拓扑场景的私有路径，称L（R2，D）是拓扑场景的公有路径。

为了考察一种拓扑场景中2个RTT序列之间的定量关系，本文利用线性回归方法给出了具体的估算方法并对估算的精度进行了定义。

设测量所得到的两个 RTT 序列为 X=（x1，x2，…，xn）和 Y=（y1，y2，…，yn），其中 xi与 yi在时刻上一一对应，则一元线性回归模型可以表示为，

k为回归方程的斜率，b为回归方程的截距。它们的计算公式分别为

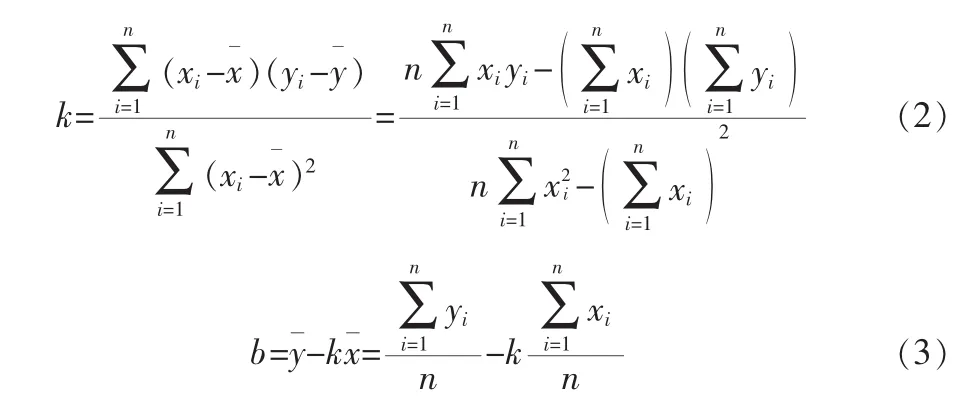
在网络中端节点之间的路径长度不大于15的假设下，本文主要通过改变仿真拓扑的路径长度，形成私有路径L（S1，R2）、私有路径 L（S2，R2）和公有路径 L（R2，D）的长度组总共包含种。对于不同的路径组合，都可以根据上述线性回归的方式确定出斜率k和截距b，然后就能够利用回归方程对同一路径组合下的时延情况进行估算。

针对1 015种路径组合的拓扑场景做类似仿真，通过分析得到斜率和截距，这些仿真结果存储在服务层节点中。为了检验用 RTT（S1，D）估算 RTT（S2，D）的精度，引入均方根误差来衡量估算的误差，p=1-RMSE作为估算精度。表1列出了对部分拓扑场景进行仿真而得到两个RTT序列的相关分析结果。

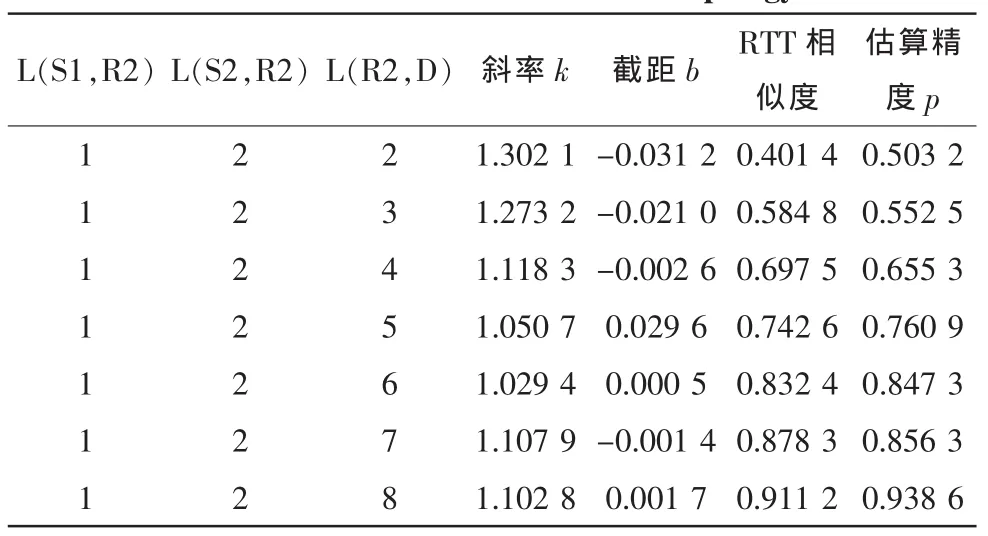
表1 一些拓扑场景的RTT相似度和估算精度结果Tab.1 Test results of sim ulation for som e topology scenarios

从上面仿真数据发现，在私有路径 L（S1，R2）和 L（S2，R2）固定时，公有路径 L（R2，D）越大，估算精度越大，即得到的时延估算值具有较高的估算精度。在其他拓扑场景中随公有路径增大，估算精度也具有增大的趋势。此现象也验证了Zhu等人[6]关于RTT相似度与路径长度的关系的相关结论。

3 时延估测总体架构

为了满足基于网络拓扑进行时延估算的需要，本文提出的时延估测系统架构，架构分为三层：服务层、测量层和应用层。时延估算系统的框图如3所示。

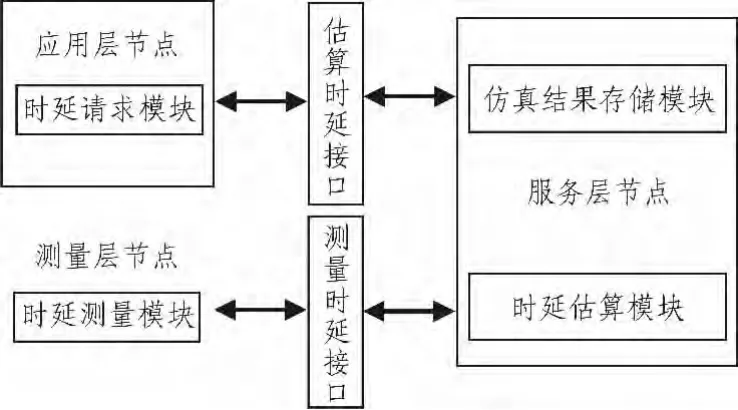
图3 时延估测系统框图Fig.3 Structure diagram of the delay estimation system

服务层可由一个或多个具有较强计算能力和存储能力的服务器组成，单个服务器可以看作是集中控制的系统，多个服务器可以组成一个分布式集群，它们之间进行协调工作。每个节点由仿真结果存储模块和时延估算模块构成。服务层节点可以定期通过现有的网络拓扑服务得到网络拓扑，并存储不同拓扑场景对应的估算公式和估算精度。由时延估算模块提供端到端时延的估算服务。

测量层由一个或多个具有测量功能的主机组成，负责测量到其他检测点和应用层节点的RTT时延，并将结果发送给服务层节点。

应用层由普通的端节点组成，根据需要向服务层请求到某个端节点的RTT时延，并且应用层节点也可以根据需要启动测量功能。

4 动态时延估算算法

基于拓扑路径长度与RTT相似度和估算精度之间的关系，并结合上文提出的时延估测架构，本文提出了一种动态的时延估算算法。假设测量层节点部署固定的情况下，应用层节点S向服务层发出的端到端时延请求，要求得到RTT（S，D），并要求时延估算精度不小于E。则根据网络拓扑中公有路径长度与估算精度之间的关系，可以从网络的测量节点集合中选择所形成拓扑场景中公有路径最大的测量点M来估测RTT（S，D）。认为M能比其他测量节点估算S到D的RTT更精确。该方法在已有测量节点不能满足精度要求时，通过新增测量节点的方案，保证时延估测系统的灵活性和高效性。

服务层节点在接收到一个节点S到D的端到端时延请求后的主要处理步骤如下：

1）服务层节点在接收到节点S到D的时延请求后，首先判断节点S是否为测量节点。如果是转到步骤2），否则转到步骤 5）；

2）直接查找S到D的测量时延；如果服务器中存在S到D的历史时延测量结果，转到步骤3），否则转到步骤4）；

3）直接返回历史时延测量值，且返回精度是1）；

4）服务层节点向测量节点S发送消息进行RTT（S，D）立即测量，直接返回最新的测量值并加入服务层节点的时延历史记录中，返回时延测量值，且返回精度是1）；

5）从网络系统中的测量集合中选择满足估算精度最大的测量节点进行估算，动态选择测量节点的标准是该测量节点与待测源节点和目的节点组成拓扑场景的估算精度最高，即选择与待测源节点S、目的节点D组成拓扑场景的公共路径长度最大的测量节点来估算RTT（S，D），此时估算值可以利用对应拓扑场景的仿真下的斜率和截距计算得到，并得到对应的时延估算精度 e。 如果 e＞E，返回 RTT（S，D）和估算精度e；否则，表明网络中部署的所有测量节点，都不能满足该RTT请求的估算精度要求E，转到步骤6）；

6）此时需要更多的测量节点的加入。源节点S启动自身的测量功能，加入测量节点集合，进行直接测量，返回RTT（S，D）测量值和估算精度1，并将测量结果发送给服务层节点存储。

为了更好地说明整个算法的流程，图4给出了算法的流程图。

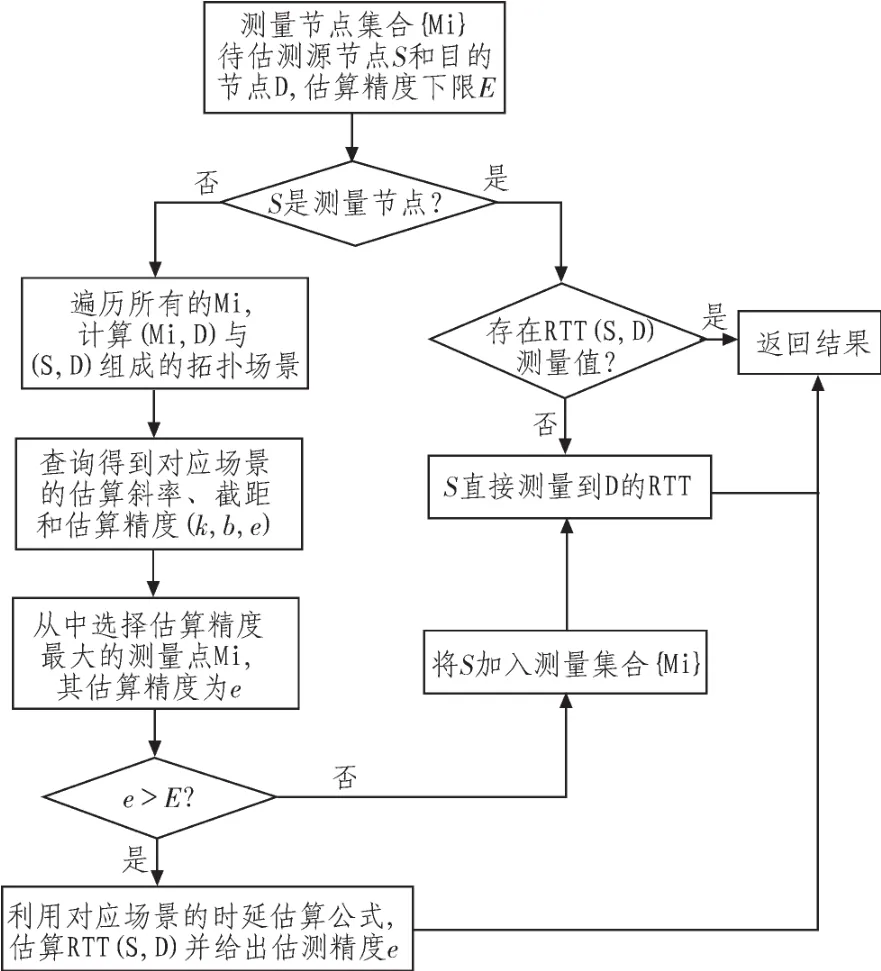
图4 时延估算算法流程图Fig.4 Flow chartof the delay estimation algorithm

5 结束语

本文在NS2网络仿真中分析了网络内部结构与网络时延之间的关系，对典型的拓扑结构进行时延测量和分析，得到网络时延RTT相似度与公有路径长度之间的定量关系。在此基础上，根据网络拓扑结构利用线性回归的方法提出了时延估算的新方法。另外考虑到不同的估算精度要求，给出了动态的时延估算模型，一方面可以动态地选择最优的测量节点，另一方面还可以在测量节点都不能满足精度要求的情况下启动自身的测量功能。

[1]邢长友，陈鸣.网络距离预测技术[J].软件学报，2009，20（9）:2470-2482.XINGChang-you，CHENMing.Techniquesofnetwork distance prediction[J].Journal of Software，2009，20（9）:2470-2482.

[2]Paul F，Sugih J，Cheng J，et al.IDMaps:A global Internet host distance estimation service[J].IEEE/ACM Transaction on Networking，2001，9（5）:525-540.

[3]Frank DaBek，Russ Cox，Frans Kaashoek，et al.Vivaldi:A decentralized network coordinate system[C]//Proceedings of the 2004 conference on Application， technologies，architectures， and protocols for computer communications，New York:ACM Press，2004:15-26.

[4]王意洁，李小勇.网络距离预测技术研究[J].软件学报，2009，20（6）:1574-1590.WANG Yi-jie，LI Xiao-yong.Network distance prediction technology research[J].Journal of Software，2009，20 （6）:1574-1590.

[5]马建国，席明贤，林益民，等.中国Internet路由级跳数测量与分析[J].计算机应用研究，2008，25（7）:2112-2114.MA Jian-guo，XI Ming-xian，LIN Yi-min，et al.Chinese Internet router-level hop countmeasurement and analysis[J].Application Research ofComputers，2008，25（7）:2112-2114.

[6]ZHU Na-fei，HE Jing-sha.Effects of path length on the similarity of network nodes based on RTT[J].Journal of Networks，2012，7（9）:1423-1430.