基于模糊软集合的水库选址综合评价方法

，

(1. 山东省定陶县水务局，山东 定陶 274100；2. 合肥工业大学计算机与信息学院，合肥 230009)

1 背景介绍

定陶县位于山东省西南部，共辖10镇2办事处，总人口64.83万，耕地面积6.222万hm2。由于该地区降水年内较集中于夏季，蓄水工程多年失修，地表水利用率很低，而且地下水开采程度不均，局部区域开采量较大，且补给不足，形成局部超采局面。在这种情况下，解决水资源短缺问题，优化水资源配置，“优水优用”，保障定陶县城乡居民饮水安全，兴建引黄水库工程迫在眉睫。因此，县政府于2012年初步选定三处水库备选地址。由于水库建设是一项投入多、影响大的不可逆性工程, 因此必须科学地、综合地加以评价, 否则就会造成资金浪费, 效益低下及其他难以挽回的损失。

因此，本文将设计一种有效的水库选址评价方法，采用模糊软集理论对水库地址备选方案进行综合模糊评价。

2 水库选址问题

2.1 评价指标的选择

由于水库建设是一项浩大的工程，需要从不同角度综合、客观、全面地评估选址方案。因此，本文在分析和总结已有工作的基础上，主要考虑以下评价指标：

a.引水条件。主要衡量水库方案能否充分利用现有的水利工程或者地下水资源，方便引水。

b.供水效能。水库建设的目的是保证城乡居民饮水，此指标主要衡量水库的地址是否方便供给城乡自来水厂。

c.防洪作用。水库能否在雨水季节起到防洪、泄洪作用。

d.工程施工条件。水库建设需要大量的材料和能源，其运输是否方便。

e.土地投入。水库尽量选择在地势低洼、耕地少、不迁占村庄的地方。

f.对环境的影响。水库的建设是否导致环境破坏，带来污染。

g.人力投入。定陶县各乡镇农村剩余劳动力分布不均，水库工程能够充分利用本县的人力资源。

h.移民影响。由于水位上升使库区被淹没，需要进行移民。并且由于兴建水库导致库区的风景名胜和文物古迹被淹没，需要进行搬迁、复原等。

值得注意的是，这些指标均存在较强的模糊性和不确定性, 选址方案好坏的评价难以定量化, 运用“精确”的数学方法来评价几乎是不可能的，采用模糊的定性概念(如: 很好, 好, 一般……)来描述便显得必要也更为合理, 因为模糊的定性概念之间不存在绝对分明的界限,更符合人脑的思维表达方式。

由于评价专家常常来自不同的领域，或者来自不同组织和部门，而且每个专家所具有的知识和经验不同，因此，每个评价专家可能只关注评价指标集中、自己感兴趣和熟悉的若干指标。但是目前常用的评价方法，如简单加权、层次分析法(Analytic hierarchy process, AHP)[9]、模糊评判法[4]等， 均要求各评价专家考虑相同的评价指标集来给出每个方案的评价信息。这些方法很容易导致各评价专家评价结果之间差异较大，引起误判，从而不利于决策者的最后决断。例如：对水库选址方案进行评估，评价专家由水利工程师、建筑工程师、人文专家构成，各个专家会优先考虑自己感兴趣的评价指标，如：水利工程师主要对引水条件、供水效能、防洪作用进行评价；建筑工程师考虑的是工程施工条件、土地投入、人力投入的情况；而人文专家着重关注的是水库对环境、移民的影响。因此，本文考虑评价专家的不同偏好，设计一种基于模糊软集合的水库选址评价方法。

2.2 问题描述

水库选址评价问题形式化描述如下：

评价专家exk根据自己的评价指标集Ck对每个方案集给出评价矩阵见式(1)，其中表示专家exk根据评价指标对方案软件st的评价值，带有一定的主观性。

(1)

因此，水库选址评价问题就是如何对不同专家的评价矩阵进行信息融合，得出每个待评价方案st的分数Score(st)。

3 模糊软集合

由于用人类语言表示的参数通常都具有模糊性，例如：对于论域中的某个对象，说它是绝对漂亮或不漂亮都是不合理的，应该用模糊语言加以描述。因此，Maji等在软集合理论的基础上提出了“模糊软集合”，并已应用到多种决策分析问题的求解。

定义1 软集合。设U为初始论域，E是参数集，P(U)为集合U的幂集，(F,E)是论域U上的一个软集合，当且仅当F是E到P(U)的一个映射。

对于∀e∈E，F(e)是具有e参数性质的U中元素的集合，即F(e)⊆U，而软集(F,E)则是由分别具有U中各个参数性质的集合所构成的近似集合。

例1 假设软集合(F,E)描述了X先生打算购买的房子(house)的特点。U是考虑的房子的集合，有六种房子，表示为U={h1,h2,h3,h4,h5,h6}。E是参数集，用于描述房子的特点，比如：昂贵(expensive)，漂亮(beautiful)，木头(wooden)，便宜(cheap)，绿化好(in the green surroundings)，表示为E={e1,e2,e3,e4,e5}。

现在我们就可以通过软集合指出哪些是昂贵的房子、漂亮的房子等。如果房子h2、h4是昂贵的，则F(e1)={h2,h4}；如果h1、h3是漂亮的，则F(e2)={h1,h3}；如果h3、h4、h5是木头的，则F(e3)={h3,h4,h5}；如果h1、h3、h5是便宜的，则F(e4)={h1,h3,h5}。因此，软集合(F,E)可以表示为

(2)

定义2 模糊软集合。设U为初始论域，E是参数集，ξ(U)代表定义在U上的模糊集，A⊆E，(F,A)是论域U上的一个模糊软集合，当且仅当F是A到ξ(U)的一个映射。

例2 考虑例1中的问题，假设模糊软集合(F,A)描述了X先生打算购买的房子(house)的特点。U={h1,h2,h3,h4,h5,h6}、A={expensive,beautiful,wooden}={e1,e2,e3}描述了房子的特点。模糊软集合就可以描述每个房子对于A中参数的符合程度。例如F(e1)={h1/0.3,h2/0.8,h3/0.9,h4/0.5,h5/1,h6/0.5}，F(e2)={h1/0.7,h2/0.9,h3/0.1,h4/0.6,h5/0.4,h6/0.3}，F(e3)={h1/0.2,h2/0.5,h3/0.7,h4/0.8,h5/0.9,h6/0.9}。

因此，模糊软集合(F,A)可以表示为

(3)

此外，模糊软集合还可以用表格进行形象的表示。如(F,A)可以表示为表1的形式。

表1模糊软集合的表格表示法

Uexpensive=e1beautiful=e2wooden=e3h10.30.70.2h20.80.90.5h30.90.10.7h40.50.60.8h510.40.9h60.50.30.9

定义3 “AND”运算。 设(F1,A)和(F2,B)是U上的两个模糊软集合，若对∀(α,β)∈A×B，H(α,β)=F1(α)∩F2(β)，则称(F1,A)∧(F2,B)=(F,A×B)为模糊软集合(F1,A)和(F2,B)的“AND”运算。

需要注意的是，模糊软集合(F,A×B)中的每个参数都是由A和B中参数“合成”得到的。如：(F1,A)的定义如例2，(F2,B)中的参数B={red,yellow,blue}描述房子的颜色，那么“红色的木头房子”则是由A中的e3和B中的e1合成得到的。

4 基于模糊软集合的水库选址评价过程

如图1所示，求解水库选址评价问题时，首先政府确定水库地址备选方案集={s1,s2,…,sq}和评价指标集I={i1,i2,…,in}；然后每个评价专家给出个人评价指标集并经过实地考察给出评价矩阵我们运用模糊软集合对所有评价专家的评价值进行信息融合，得到最终评价结果。

图1 基于模糊软集合的水库选址评价过程

县政府经过讨论，初步选定3个地点作为备选水库地址，具体位置详见图2。

图2 备选方案的分布图

备选方案1：该处位于马集镇和定陶县城交界处、大刘楼行政村东，为马集镇废旧窑场和低洼盐碱地，常年积水；范围内有约4hm2的垃圾场和废旧窑场约11.33hm2；备选库址区紧邻菏曹运河。

备选方案2：该处位于南王店镇李庒行政村北，为南王店镇窑厂和低洼盐碱地，窑厂占地约6.67hm2，目前在运营。窑厂附近有耕地。

备选方案3：该处位于定陶县城东侧、孔楼行政村旁。该处为铁路和公路的交汇处，交通发达，人口多，耕地多。

基于模糊软集合的水库选址评价过程可以描述如下：

a.将R1、R2、R3表示成模糊软集合(F1,R1)，(F2,R2)、(F3,R3)，见式(4)～式(6)。

(4)

(5)

(6)

b.利用模糊软集合对R1、R2、R3进行信息融合，即对模糊软集合(F1,R1)、(F2,R2)、(F3,R3)进行“AND”运算，得到的融合结果为

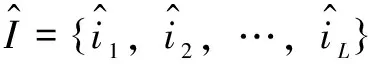
(7)

如果水利工程师对某方案的引水条件的评价为0.7，而建筑工程师对此方案的工程施工条件评价为0.9，则经过信息融合可以得出，此款方案的评价结果为0.7，也就是“引水条件好，工程施工条件又好的”的评价值为0.7。

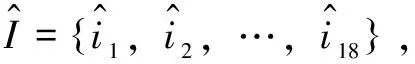
根据式(7)，计算模糊软集合(F,R)，其表格形式见表3。

i^numi^1i^2i^3i^4i^5i^6i^7i^8i^9原始参数i1i4i7i1i4i8i1i5i7i1i5i8i1i6i7i1i6i8i2i4i7i2i4i8i2i5i7i^numi^10i^11i^12i^13i^14i^15i^16i^17i^18原始参数i2i5i8i2i6i7i2i6i8i3i4i7i3i4i8i3i5i7i3i5i8i3i6i7i3i6i8

表3模糊软集合(F,R)的表格形式

i^numi^1i^2i^3i^4i^5i^6i^7i^8i^9s10.80.70.90.70.60.60.70.70.7s20.60.60.70.70.70.70.60.60.6s30.60.50.60.50.60.50.70.50.6

续表

c.计算对比表(Comparison-table)。根据表3计算对比表CT=(ctxy)q×q，其中

(8)

(9)

显然ctxy是非负整数，通俗地讲，ctxy指的是：对于所有的评价参数，方案sx的综合评价值高于方案sy的评价参数的个数。计算结果见表4。

表4对比表

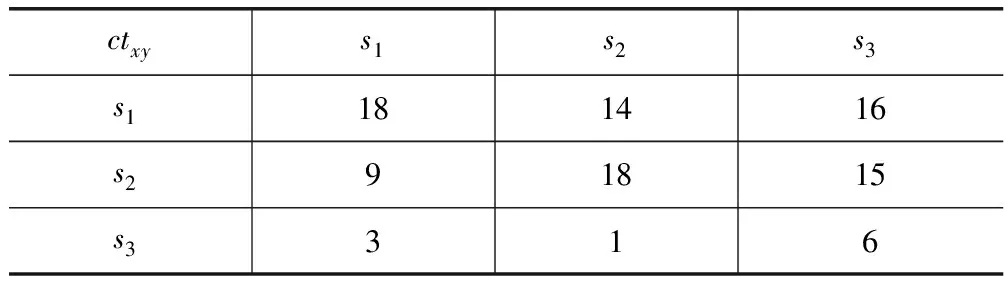
ctxys1s2s3s1181416s291815s3316

d.计算评价得分。根据表4，计算每个评价方案的得分盾Score(st)。其中

Score(st)=xt-yt

(10)

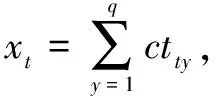
表5评价得分值

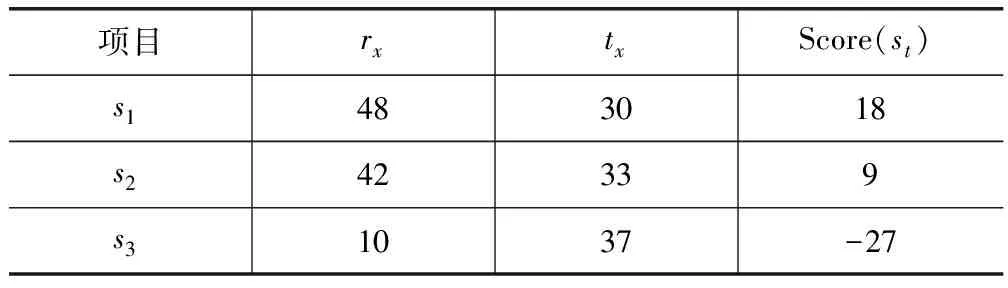
项目rxtxScore(st)s1483018s242339s31037-27

显然Score(s1)>Score(s2)>Score(s3)，因此，方案s1最优，其次是s2和s3。

5 结 语

由于水库选址时考虑的因素众多，难以用定量的方法进行描述，采用此方法的意义在于可以反映评判专家的不同偏好和评价信息的不确定性，使评价专家能灵活地表达其主观判断；采用模糊软集合的“AND”运算可以融合多个评价者的评价信息，获得综合的评判结果。

本文获得的结果为定陶县政府的水库建设提出了决策依据。

[1] 刘宝军,张金宏.我国的水库建设与防洪[J].中国水利，1999(7).

[2] 蔡其华.充分考虑河流生态系统保护因素 完善水库调度方式[J]. 中国水利，2006(2)：14-17.

[3] 胡宝柱, 高磊磊, 王娜.水库建设对生态环境的影响分析[J]. 浙江水利水电专科学校学报，2008，20(2)：41-43.

[4] 张俊华,高承恩,陈南祥.水库建设对生态环境影响的评价[J]. 安徽农业科学,2011, 39(5): 2876-2878, 2916.

[5] 刘晓星,刘福旺.菏泽建设饮水安全引黄平原水库的思考[J].中国水利,2013(18):42-44.

[6] 马琳,张洪美.浅析水库建设对环境的影响[J].山东水利,2010(8):27-28.

[7] 魏津生.人口迁移理论与水库移民研究[J]. 中国水利, 2011(2):7-10.

[8] 黄金池,何晓燕.浅析水库设计洪水与风险管理[J]. 中国水利, 2005(15):61-63.

[9] 李红,杨小凯. 利用层次分析法确定水库选址问题[J]. 海河水利, 2004(4):54-58.

[10] Maji P K, Biswas R, Roy A R. Fuzzy soft sets[J]. Fuzzy Math, 2001(9):589-602.

[11] Maji P K, Roy A R. An application of soft sets in a decision making problem[J]. Comput. Math, 2002(44):1077-1083.