一种基于红外视频图像电力设施故障识别方法
周 煜
(国家电网公司华北电力调控分中心,北京 100053)
随着现代社会电力资源需求愈发提高,给电力系统运行带来了巨大压力,电力设施故障出现频率越来越高。由于电力设施一般广泛分布于农村、城市、山区,检修部门人力资源有限,难以第一时间发现故障并加以排除。因此,对电力设施故障进行红外在线监测是一个较为理想的方法。
由于红外监测图像的成像环境复杂,以及红外图像本身所具有低对比度的特性,这使得获取的监测图像中或多或少存在一些噪声,导致图像质量有所下降。因此,有必要对该类图像进行预处理,以最佳恢复图像所刻画的真实信息,这样势必有助于提高电力设施的识别准确率,避免误判。在该领域,相关学者也做了一些工作,金立军[1]等通过借助于图像处理方法对电力设备放电现象进行检测研究,魏立明[2]等将图像增强和检测方法对电力设备故障进行诊断,吴晓东等[3]通过图像分割方法成功地从SAR图像中检测出电力线等信息。
受到上述各项研究成果的启发,本文首先对红外监控降质图像预处理算法进行研究,然后实现基于复原图像的电力设施故障识别。
1 提升小波变换实现步骤分析
提升小波变换[4-5]相对于经典小波变换而言,具有更高精度,信号分解与重构单层提升小波变换的主要步骤为:
1)分解(Split),将上述信号集合分解成偶序列η2j和奇数序列φ2j-1,并且这两类序列彼此互不相交,该步骤中图像信号序列可表示为

2)预测(Predict),该步骤是基于图像信号间存在相关性这一前提,采用相邻信号偶数序列对奇数序列进行预测,通过对奇数序列的真实值与预测值作差,该差值可称之为细节系数,预测步骤为

式中:D2j-1为细节系数;p[⋅]代表预测算子。
3)更新(Update),采用更新算子U[⋅]对步骤2)中产生的序列D2j-1进行更新,其过程为

2 本文算法基本思路
2.1 高频部分处理
图像经过提升小波变换后,获得低频系数和不同方向的高频系数,低频部分包含图像中的背景信息;高频系数则是图像中边缘、轮廓线、突变点的反映,对于降质的红外电力设施监控图像而言,该部分还包含一些降质信息——噪声。对于高频部分分解系数可以通过图1进行形象化的描述。

图1 高频部分分解系数
本文提出一种基于分解窗口的自适应加权改进中值滤波算法,基本思路是:将大小为m×m的滤波窗口分解成m个大小为1×m的子窗口,通过对各子窗口分解进行自适应加权中值滤波,待各子窗口滤波完毕,即获得一个m×1的新型窗口,再次通过对该窗口进行自适应加权中值滤波,从而将最终滤波结果加以输出,如图2所示。
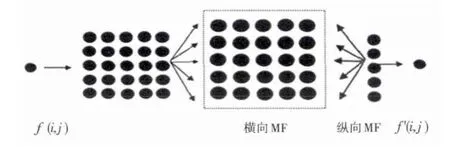
图2 本文改进自适应中值滤波算法基本流程
相对于以往的加权中值滤波,本文算法的特点有:1)窗口可分解性,即小波域中不同方向分布的子图像通过滤波窗口加以分解,以尽可能保持图像信息的连续性;2)权重的自适应性,即权重的设置依赖于各分解窗口中像素数量以及像素间几何距离大小这两类因素。下文以大小5×5的滤波窗口为例,结合不同方向分布的小波分解子图像分别加以讨论。
2.1.1 水平方向分布的高频部分处理
1)以图1中各个1×5子窗口的中心像素点fx(i,j)(x∈[1,5])作为待滤波点,计算其余各点与该点的几何距离为

权重P水平可进行如下计算

通过各点灰度值(除中心点外)分别乘以各自权重,在此基础上做和运算

式中:f′水平(i,j)即为1×5窗口的滤波结果;{f水平(i,j)}为该窗口中除中心点外的像素点集合。
2)通过采用1)中方法完成其余4个1×5窗口的滤波,即获得一个新型滤波值集合

3)统计式(7)集合中元素数目N1,若大于3则进行经典中值滤波,否则取所有元素均值作为最终滤波值输出。
2.1.2 水平方向分布的高频部分处理
1)统计1×5子窗口中像素点个数N2,若N2=1,则将该点不作处理直接输出;若N2=2,则取两点均值加以输出;若N2≥3,则对其进行经典中值滤波,输出滤波值。
2)经过处理后,获得一个新集合
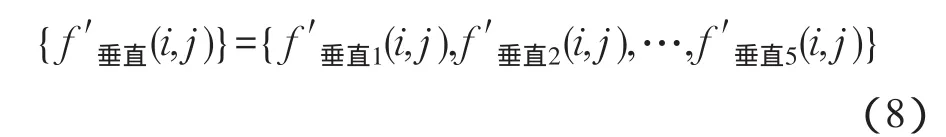
3)对于式(8)所描述的集合,首先以该集合中点作为待滤波点,计算其余各像素点与该点的几何距离

然后,权重P垂直可计算成
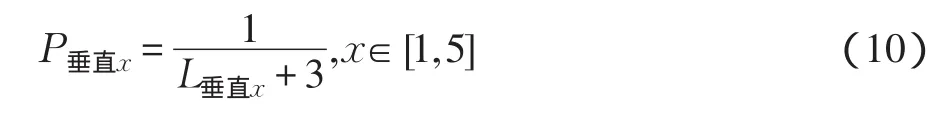
将该集合中除中心点外的各点灰度值分别乘以各自对应的权重,再进行求和运算,所得结果即为滤波值。
2.1.3 对角方向分布的高频部分处理步骤
1)统计1×5子窗口中像素点数目N3,若N3>3,则忽略各点几何距离因素,直接进行中值滤波即等权中值滤波;否则将该窗口所有点灰度值均值作为滤波结果输出。
2)对于步骤1)中所获取的滤波点的集合{f′对角(i,j)}={f′对角1(i,j),f′对角2(i,j),…,f′对角5(i,j)},分 别求其中间值和均值。
以上针对水平、垂直、对角三类小波分解子图像分别给出了本文改进自适应中值滤波算法基本实现步骤,通过分别对各方向的小波分解子图像进行较为精细的滤波,以便消除其中所包含的噪声。
2.2 低频部分处理
电力设施红外监控降质图像经过提升小波变换后,获得的低频分解系数尽管包含了图像绝大多数信息,受到噪声污染程度低,但如果对该部分噪声不加考虑,则对最终的重构图像质量会有所影响。因此,对于该部分分解系数,提出一种改进型阈值函数模型为

式中:为小波系数幅值;T′为阈值。该模型在经典小波阈值[6]的基础上,通过对经典恒定偏差T引入一个修正因子,使得该恒定偏差会随着小波分解层数的变化而自适应调整,从而对经典小波软阈值在处理图像时容易出现的不连续性这一缺陷进行适当修正。但经典阈值,该阈值总体上为全局阈值,一方面随着小波分解层数的增大各分解系数幅值会有所衰减;另一方面,小波低频分解系数幅值均比较大,如果采用该阈值进行处理,容易将相当一部分图像信息置0,因此,该全局阈值无法适应小波系数的精细化处理。基于以上分析,本文对该阈值引入了小波分解层数信息进行适当改进,即

式中:σ为噪声方差;n为图像信号大小。该阈值随着分解层数的增大而自适应降低,这符合图像小波分解特征。本文提出的改进型阈值函数模型为
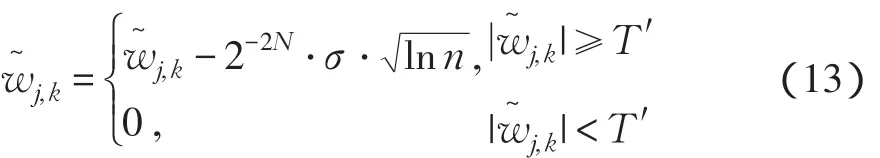
2.3 重构图像增强方法
针对小波重构图像在一定程度上会有所失真,因此有必要对重构图像进行后处理。就图像信息而言,大体上有如下几类:1)目标信息,该部分是图像中的感兴趣信息,即为电力设备故障所在区域信息;2)背景信息,该信息即为图像中的灰度值较低的部分信息;3)过渡信息,该部分信息介于上述两类信息间,且有助于目标信息的判别。有必要对上述3类信息加以区分,对于背景信息加以抑制,对于目标信息适当增强,因此,提出一种基于图像分类信息的自适应增强方法:首先整幅图像中灰度最大值和最小值,将两者均值作为图像信息初始分类阈值t;然后对该阈值进行上下延拓,获得阈值区间,该区间中的图像信息可认定为过渡信息,小于或大于该区间的即为背景信息和目标信息。根据这一分类,对于目标信息区域进行自适应同态滤波,过渡区域则不作处理,背景信息则进行适当抑制。据此,本文图像自适应增强方法为

式中:f(i,j)代表图像中任意一点灰度值;t为阈值。
3 实验仿真
3.1 实验方案一
采用2幅电力设施故障监测降质热红外图像作为数据,经过文献[7]、文献[8]以及本文算法处理后,其结果对应于表1和图4、图5所示。

表1 本文2幅图像的PSNR,RMSE计算结果
采用文献[7]和文献[8]以及本文算法分别对图4a和图5a降质的热红外电力设施监控图像进行复原,本文算法对两类降质图像复原后图像质量明显改善,基本排除了图像中噪声的干扰,而其余两类算法处理后的图像中仍存在不同程度的模糊;本文算法的PSNR值高于文献[7]约2~3 dB,高于文献[8]约1~2 dB,且RMSE值也明显低于其余两类算法,这可以反映出采用本文算法复原得到的图像质量较好。

图4 第一幅图像处理结果对比

图5 第二幅图像处理结果对比
3.2 实验方案二
对实地拍摄的100幅故障图像从中分别抽取5幅图像、10幅图像、15幅图像、20幅图像、25幅图像,通过目视解译与实地调查相结合的方法来验证识别的准确率(记为方法2),并与直接通过降质图像进行故障识别的准确率进行对比(记为方法1),实验结果如表2所示。
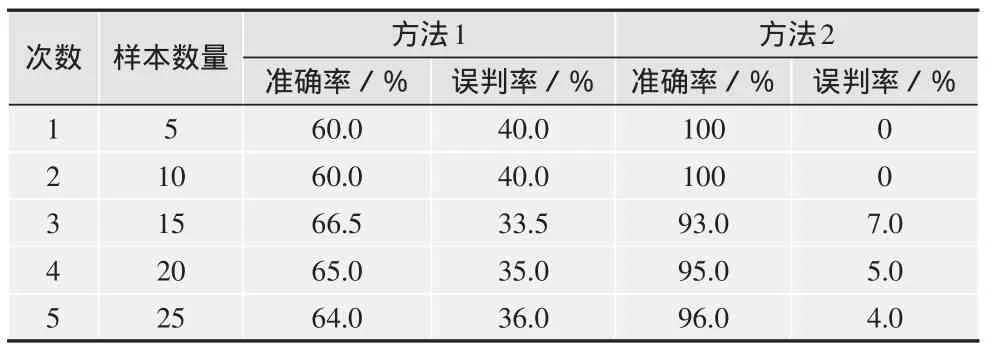
表2 实验结果对比
通过简单计算可以看出,方法1故障识别的准确率平均值为63.1%,方法2故障识别的准确率平均值为96.8%,这可以说明,本文所提出的图像复原算法对于提高电力设施故障识别准确率是有所帮助的。
4 结束语
本文提出了一种基于红外视频图像复原的故障识别方法。实验证明,本文算法复原图像质量优于部分已有算法,且通过本文算法复原图像后,再进行故障识别,其准确率明显提高。
[1] 余立军,陈俊佑,张文豪,等.基于图像处理技术的电力设备局部放电紫外成像检测[J].电力系统保护与控制,2013,41(8):43-48.
[2] 魏立明,杨天野.基于图像增强和边缘检测的电力设备故障诊断研究[J].吉林建筑工程学院学报,2012,29(4):84-86.
[3] 吴晓东,李瑛,刘晓伟,等.基于多尺度联合分割的SAR图像电力线走廊变化检测[J].电力科学与技术学报,2012,27(4):51-55.
[4] 黄德天,吴志勇.提升小波变换在NAS-RIF盲复原算法中的应用[J].计算机辅助设计与图形学学报,2012,24(12):1614-1620.
[5] 刘艳萍,高国荣,龚宁,等.提升小波变换与中值滤波的红外光谱消噪[J].光谱学与光谱分析,2012,32(8):2085-2088.
[6] 王瑞,张友纯.新阈值函数下的小波阈值去噪[J].计算机工程与应用,2013,49(15):215-218.
[7] 余光华.一种结合图像增强的高斯噪声组合滤波算法[J].电视技术,2013,37(15):11-14.
[8] 王德旺,王改利.自适应中值滤波在云雷达数据预处理的应用[J].激光技术,2012,36(2):221-114.

