40Ar/39Ar年代学中几个重要问题的讨论*

王非 师文贝 朱日祥

中国科学院地质与地球物理研究所岩石圈演化国家重点实验室，北京 100029

1 引言

作为最为成熟的年代学手段之一，40Ar/39Ar年代学除为地质事件标定时间外，它所涉及的元素或同位素的迁移分布和地质过程之间的关系，使得其内涵远远超越了“年龄测定”这一概念。

作为重要的同位素定年手段，随着稀有气体分析技术的发展，可以说，目前40Ar/39Ar法已成为无论在精确度还是在准确度上均为最可靠的手段之一，广泛应用于重大地质事件(如磁极倒转，生物灭绝，地幔柱形成，火山喷发，陨石撞击等)、地质单元界线的精确定年，并为地质年表提供“金钉子”般的年龄制约。作为稀有气体之一的Ar，其不易和其他物质发生反应的特点使其基本遵守热扩散方程，Ar 的扩散与分布与温度呈函数关系，从而记录了其经历的热历史；而岩石圈内发生的地质过程总是和热作用密切相关，当温度降至一定值时，矿物中的Ar的分布就“冻结”了地质热历史的最后状态，通过实验室工作就可以由此“最后状态”反演地质作用过程。因此，40Ar/39Ar年代学成为研究地质热历史的重要手段，建立在其上的定量模型被广泛应用于地质热历史的研究，是定量研究岩浆上升速率、造山带形成、断层活动、结晶基底剥露等和热作用相关的动力学过程的重要手段。此外，由于其定年使用的母体为常量元素钾，且在质谱上实现分析时只需测定同位素比值，因此相比其他在定年中需要测定元素含量的手段(如U-Pb)而言，40Ar/39Ar年代学还是测定年轻(其下限已至数千年)地质体的重要断代手段，并且几乎是中晚更新世范围内(30万至200万年)唯一可靠的定年方法。

近年来，研究的深入，40Ar/39Ar年代学在各方面取得了众多新的进展，但也出现一些了新的问题，这些问题对无论在方法学研究还是地质应用方面都具有重要的影响。例如，我们在年轻(<1Ma)火山岩中的反等时线中极少发现过剩Ar。从形成机制上讲，和年老的火山岩相比，年轻火山岩对过剩Ar的“免疫”是难以理解的。再如，压力是否影响Ar同位素体系的封闭温度？常规意义上的封闭温度是不考虑压力的影响因素的，但对于来自地壳深部、或高压超高压变质带的地质样品，对压力影响的考虑是非常自然的。还有，自从多重扩散域(MDD)模型问世后，伴随着该方法的广泛应用是持续不断的质疑。那么该方法是否还有应用价值？该怎样使用它？是很多构造学家非常关心的问题。

本文主要展示了作者多年来的一些研究体会、发现的一些问题及思考，希望能起到抛砖引玉的作用，推动对40Ar/39Ar年代学的深入研究。

2 40Ar/39Ar法目前的准确度与精确度

40Ar/39Ar法和锆石U-Pb法一起被称为“金钉子”定年手段，是地质年表年龄控制的关键手段。那么，目前40Ar/39Ar法到底能测多准？和U-Pb法相比，其精度又如何？

Fish Canyon Tuff是发育于美国南科罗拉多的一套渐新世酸性凝灰岩，其中广泛发育透长石，由于其K含量高，40Ar*/K(40Ar*为放射性成因40Ar)比值均一稳定而成为目前40Ar/39Ar法最好的标准样品。Fish Canyon透长石(FCs)在国际上被广泛应用，也是实验室之间进行对比标定的重要标准，40Ar/39Ar年龄数据。另外，U-Pb法、Rb-Sr法、裂变径迹法、(U-Th)/He法也广泛应用于该凝灰岩的定年和对比标定研究。这些研究积累的大量数据，为进行精确度与准确度的评价提供了良好的数据库。

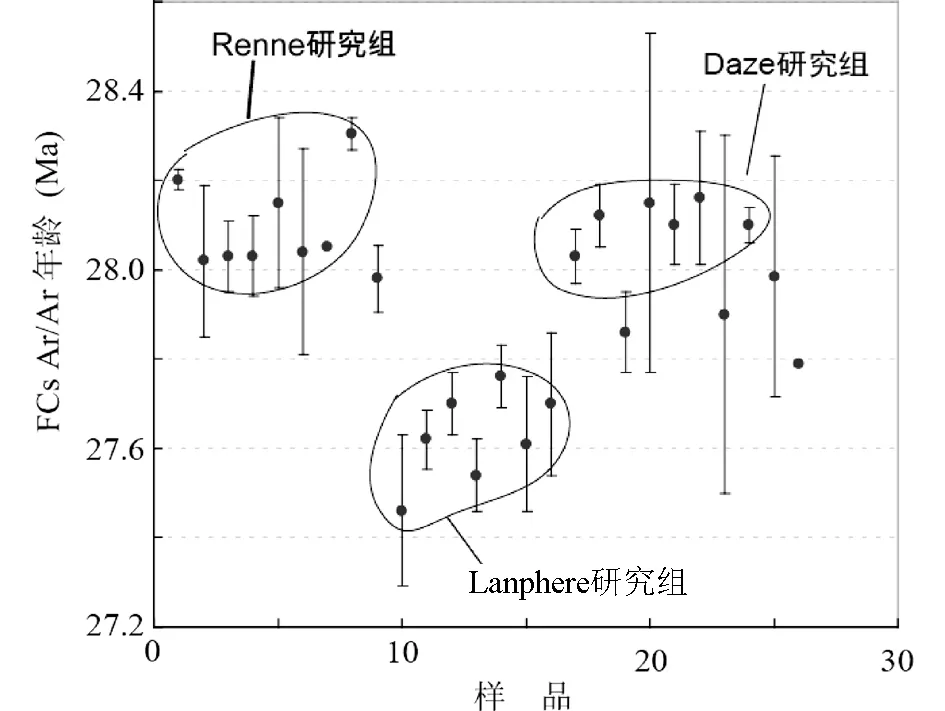
图1 由表1数据所做的 FCs年龄离散图图中标出了Renne、Daze和Lanphere研究组的数据区域Fig.1 The scatter of the FCs ages based on Table 1Different research group are denoted

2.1 准确度

不同研究者(实验室)对FCs重复测定结果见表1(Stevenetal., 1967; Hurford and Hammerschmidt, 1985; Renne, 1998; Renne and Min, 1998; Renneetal., 1994, 2010; Cebulaetal., 1986; Minetal., 2000; Villeneuveetal., 2000; Lanphere and Baadsgaard, 1997, 2001; Spell and McDougall, 2003; Dazéetal., 2003; Jourdan and Renne, 2007; Kuiperetal., 2008)，其中年龄的误差水平为2σ。

将表1中的数据投图可显示FCs年龄数据的离散情况(图1)。图中实线圈定的分别为Renne研究组、Lanphere研究组和Daze研究组的数据分布(图1)。划为一组的依据是使用相同的实验室进行分析，或属于同组的成员的分析结果(表1)。总体而言，相同的研究组给出的年龄值离散度较小，每个组内的离散度约1%；而不同的研究组之间的离散度较大，如Renne研究组 (Renne, 1998; Renne and Mi, 1998) 和Lanphere研究组 (Lanphere and Baadsgaard, 1997, 2001) 的平均值之间相差约1.7%。FCs是非常理想且广泛使用的40Ar/39Ar定年矿物，因此该样品的离散度应该反映了目前40Ar/39Ar法测年准确度的最好水平，即在～1%内可重复。

实际上，这样的准确度也代表了目前所有其它同位素定年方法的最好水平。以另一个“金钉子”手段U-Pb法为例，表2的Fishcanyon凝灰岩中锆石的U-Pb年龄离散度在3%左右，如果剔除了27.52Ma这一最低值，其离散度在1.4%左右。

造成年龄数据离散的原因可能有：1)实验室之间的系统误差；2)自然界物质的不均一性；3)实验流程的差别。

一般来讲，随着实验室的开放、实验室之间的对比标定，实验室之间的系统误差几乎可以忽略不计。从表1和图1看似乎Renne实验室和Lanphere实验室之间存在着系统误差， 但表3表明不管用什么方法， 各个研究组内部的结果总是一致的，而研究组之间的差别总是显著，这显然不能用实验室之间的系统误差来解释。

表1 FCs标样40Ar/39Ar、K-Ar年龄分析结果

Table 1 Fish Canyon sanidine40Ar/39Ar ages

方法(样品编号)年龄(Ma) 文献研究组#K⁃Ar27985±027Stevenetal．，1967K⁃Ar279±04HurfordandHammerschmidt，1985Ar/Ar激光全熔2802±017Renne，1998Renne研究组Ar/Ar常规全熔2779Cebulaetal．，1986APTS∗2803±009Renneetal．，1994Renne研究组APTS∗2815±019Dazéetal．，2003Ar/Ar激光全熔2804±023RenneandMin，1998Renne研究组Ar/Ar激光全熔(FCs)2805Minetal．，2000Renne研究组Ar/Ar激光全熔(FCs))2798±0075Villeneuveetal．，2000Ar/Ar常规全熔(79COLE⁃5)2746±017LanphereandBaadsgaard，1997Lanphere研究组Ar/Ar激光全熔(79COLE⁃5)2762±0065LanphereandBaadsgaard，2001Lanphere研究组Ar/Ar激光全熔(BGC)2770±007LanphereandBaadsgaard，2001Lanphere研究组Ar/Ar激光全熔(FCT87)2754±008LanphereandBaadsgaard，2001Lanphere研究组Ar/Ar激光全熔(79COLE⁃5)2776±007LanphereandBaadsgaard，2001Lanphere研究组Ar/Ar常规阶段升温(79COLE⁃5)2761±015LanphereandBaadsgaard，2001Lanphere研究组Ar/Ar常规阶段升温(FCT2)2770±016LanphereandBaadsgaard，2001Lanphere研究组Ar/Ar激光全熔(USGC)2810±004SpellandMcDougall，2003Ar/Ar常规全熔(956)2803±006Dazéetal．，2003Daze研究组Ar/Ar常规全熔(957)2812±007Dazéetal．，2003Daze研究组Ar/Ar常规全熔(958)2786±009Dazéetal．，2003Daze研究组Ar/Ar常规阶段升温(959)2815±038Dazéetal．，2003Daze研究组Ar/Ar常规全熔(960)2810±009Dazéetal．，2003Daze研究组Ar/Ar常规阶段升温(1103)2816±015Dazéetal．，2003Daze研究组Ar/Ar激光全熔2803±008JourdanandRenne，2007Renne研究组Ar/Ar轨道调谐28201±0023Kuiperetal．，2008Renne研究组Ar/Ar激光全熔28305±0036Renneetal．，2010Renne研究组

注：*APTS为“Astronomically (calibrated geomagnetic) polarity time scale”之缩写，即经地球轨道调谐校正之地磁极性年龄.#研究组的划分依据为使用相同的实验室进行分析，或属于同组的成员的分析结果

表2 Fish Canyon凝灰岩锆石U-Pb年龄(Ma)

Table 2 Some U-Pb ages (Ma) of Fishcabyon zircon

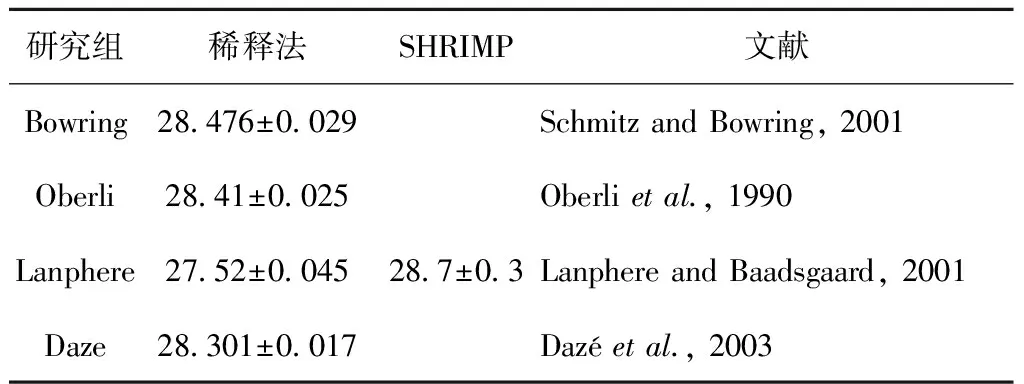
研究组稀释法SHRIMP文献Bowring28476±0029SchmitzandBowring，2001Oberli2841±0025Oberlietal．，1990Lanphere2752±0045287±03LanphereandBaadsgaard，2001Daze28301±0017 Dazéetal．，2003

自然界物质的绝对非均一性可能导致年龄的离散，这种影响在微区微量样品定年中尤其显著。表1中列出的FCs年龄的离散是否是这一因素造成的呢？从后面的讨论看,这是造成年龄离散的一个重要因素。

矿物之间的差异性可能不是造成年龄离散的原因，因为相同的研究组对Fish Canyon凝灰岩中不同矿物定年的结果是一致的(表4)。

表3不同方法对Fish Canyon凝灰岩测定结果(Ma)对比

Table 3 Comparison of ages (Ma) by various methods on Fish Canyon tuff

研究组透长石Ar/Ar锆石U⁃Pb透长石APTS文献Renne2802±0162803±009RenneandMin，1998Lanphere2754±0082752±0045 LanphereandBaadsgaard，2001

表4 Fishcanyon凝灰岩不同矿物40Ar/39Ar测定结果(Ma)对比

Table 4 Comparison of40Ar/39Ar ages (Ma) on various minerals of Fishcanyon tuff

研究组透长石黑云母角闪石文献Lanphere2754±0082762±0082753LanphereandBaadsgaard，1997，2001Daze2812±0072822±049 Dazéetal．，2003

各个实验室的40Ar/39Ar法实验流程是不统一的，不同的实验室采用不同的样品处理方法、仪器分析流程、数据处理软件，这可能引起数据的离散。此外，从上面的数据也可以看出，人为因素也是一个重要的离散来源。2009年以来国际同行在不同的场合已就这些问题进行了富有建设性的讨论，希望能建立一套标准流程，避免这些因素造成的数据偏差。

2.2 精确度

40Ar/39Ar法年龄误差主要来源于四个方面(Renneetal., 2010; Kuiperetal., 2008)：1)标样年龄的误差；2)J值的误差—由样品在原子能反应堆照射带来的误差；3)40K衰变常数的误差；4)稀有气体质谱仪的性能。其中，第二方面的误差取决于反应堆的质量，而仪器性能造成的误差取决于质谱技术的进展。年代学家们多年来致力于第一和第三方面误差的减小。

40Ar/39Ar定年是通过和标准样对比来获得年龄。目前国际上通用的标样年龄通常由K-Ar法确定。K-Ar法年龄的测定需要加入38Ar稀释剂，而38Ar稀释剂的绝对含量也需要通过标样来进行标定。虽然有时也采用“绝对标定法”，即由其他定年方法(如Rb-Sr法、U-Pb法等)确定年龄的地质样品作为标样，但大部分情况下是采用40Ar/39Ar标样来标定38Ar稀释剂的绝对含量。因此这种循环标定会造成误差的相互传递，并最终传递到地质样品中去。因此，标样的准确标定就成为减小误差的重要步骤。

Kuiperetal. (2008) 通过地球轨道协调法对标样FCs进行了迄今为止最为精确的标定，得到的年龄为28.201±0.046Ma，相对误差为0.16%(2σ)，包括衰变常数与轨道周期误差)。该年龄的精确度应该代表了目前40Ar/39Ar法年龄单次测定的最好水平。

实际上，相对于标样的误差来说，目前更紧迫的工作是重新厘定40K的衰变常数。现在所用的40K衰变常数为Steiger and Jäger (1977)确定的值(Renneetal., 2010)，为5.543(±0.01)×10-10/年。普遍认为该值偏低且误差较大，造成40Ar/39Ar法和U-Pb法的年龄之间系统偏差 (Renne, 1998; Renne and Min, 1998; Oberlietal., 1990; Schmitz and Bowring, 2001; Renneetal., 2000)。表5给出了不同时间段的一些“理想”火山岩的U-Pb和40Ar/39Ar年龄测定结果。可以看出，和U-Pb年龄相比，40Ar/39Ar年龄系统性地偏低。

值得深入了解的是，这种偏低是否为岩浆在岩浆房中驻留造成的呢？研究表明(Condominesetal., 2003)，火山岩岩浆在喷发至地表前可能在岩浆房中驻留一定的时间，其范围在几万年至20万年(Condominesetal., 2003)，其间岩浆的温度可能降至700℃，导致锆石U-Pb体系在岩浆房中封闭而开始计时，而Ar同位素体系显然只能在岩浆喷出地表时才开始封闭计时，从而导致火山岩40Ar/39Ar年龄比U-Pb年龄年轻。这对年轻火山岩(比如<1Ma的火山岩)来说特别值得注意(Condominesetal., 2003)，但却不是表5中年龄偏低的主要原因，虽然其中必然有岩浆驻留造成的偏低。因为岩浆驻留造成的偏低不会超过20万年，对于表5中的样品来说在误差范围(～0.5%)之内是无法分辨出来的。当然，随着质谱技术发展，当测定的精度大大提高时，这种岩浆驻留造成的偏差将来一定可以分辨出来的。就目前或以前的质谱分析技术来看，表5中样品的误差完全掩盖了岩浆驻留时间造成的偏差。因此，表5中明显的年龄偏差只能是别的因素造成的。从年龄越老偏差越大的系统性来看，最可能的就是40Ar衰变常数造成的。因此需要对40Ar的衰变常数进行重新厘定。

表540Ar/39Ar法和U-Pb法对火山岩样品的定年结果(Ma)比较

Table 540Ar/39Ar ages and U-Pb ages (Ma) for some “ideal samples”

岩体U⁃Pb年龄40Ar/39Ar文献FishCanyon凝灰岩284±01280±04Renneetal．，1998Siberian玄武岩2513±102500±40Renneetal．，2000Palisade流纹岩1098±41088±15Minetal．，2000Acapulco陨石4554±124507±50Renneetal．，2010

表6应用新衰变常数重新计算的表5

Table 6 Recalculated ages of on samples of Table 5 using new decay constant

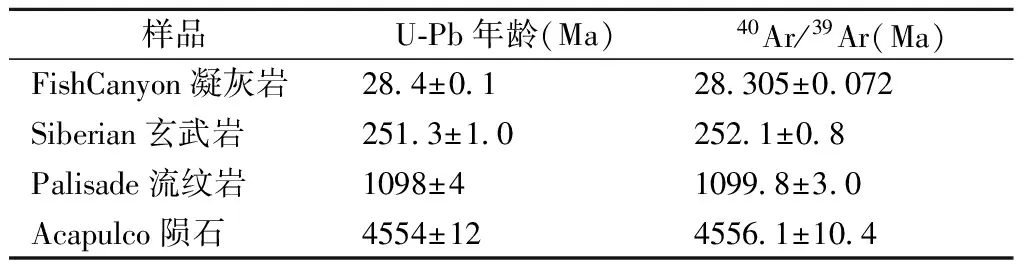
样品U⁃Pb年龄(Ma)40Ar/39Ar(Ma)FishCanyon凝灰岩284±0128305±0072Siberian玄武岩2513±102521±08Palisade流纹岩1098±410998±30Acapulco陨石4554±1245561±104

Renneetal.(2010)人通过对一系列酸性火山岩的40Ar/39Ar和U-Pb年龄对、放射性参数和标样的同位素数据共同拟合获得了新的40K衰变常数：5.5492(±0.0093)(10-10/年，并使其精度提高到0.167%(2σ)。新的衰变常数重新计算的40Ar/39Ar年龄和U-Pb法基本一致，误差也大幅度减小(表6)。

通过上述校正，40Ar/39Ar法的精度目前已提高到0.1%～0.2%，并在大多数情况下已超过了U-Pb法的年龄精度，如图2所示 (Renneetal., 2010)。

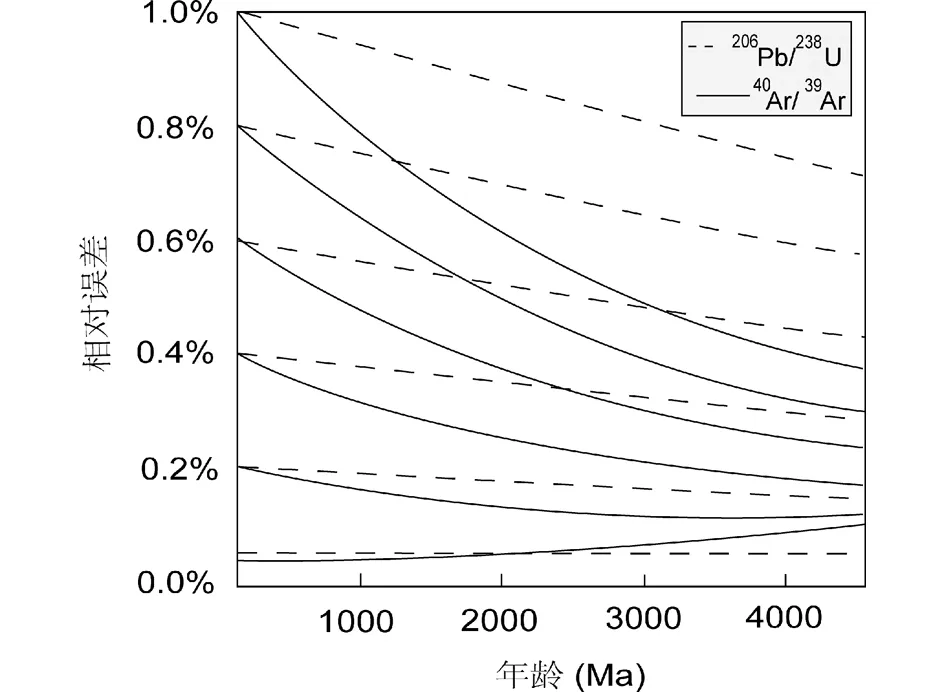
图2 40K衰变常数校正后的40Ar/39Ar法和U-Pb法理论误差比较纵坐标为年龄的相对误差，其不同的值对应于不同情况下同位素的测试误差.40Ar/39Ar法是以FCs为标准样品，U-Pb法是指206Pb/238U年龄(需要注意的是U-Pb法在年龄较大，如大于1000Ma时常习惯用207Pb/238U年龄，如有Pb丢失的话习惯用207Pb/206Pb年龄).可以看出，除了相对误差在0.05%级别外，其他情况下40Ar/39Ar法的精度要好于U-Pb法 (Renne et al., 2010)Fig.2 Summary of the accuracy of 40Ar/39Ar ages calculated with the results of this work, compared with the 206Pb/238U systemThe 40Ar/39Ar system of sample is relative to that of the FCs standard. The data show that in the most circumstance, the 40Ar/39Ar ages are more precious than that of U-Pb (Renne et al., 2010)

综上所述，通过近年来的努力，40Ar/39Ar法的精确度已得到很大的提高，达到甚至超过了U-Pb法的精度，成为最为精确的同位素定年手段之一(Renneetal., 2010)。精确度的提高使得获得的年龄误差更小，不仅可以提供数据的离散程度信息，还大大提高了年龄的分辨率，这对分辨细微的地质过程、确定它们的时间序列意义重大。

相对而言，准确度的研究仍然是摆在我们面前的严肃课题，这不仅是40Ar/39Ar法所面临的课题，也是所有其他同位素定年手段所面临的课题。这其中固然有“自然的”因素，如没有人知道“真值”是多少，从而难以做出判断，仪器性能不够“精良”，难以分辨样品中的细微变化，样品的“绝对非均一性”造成从不同的层级或角度看具有不同的结果等，但也有人为的因素，如实验流程各异、样品处理方法不同、数据计算处理不同等。

图3 重复测定的FCs阶段升温年龄谱所使用的标样为FCT透长石 (28.020Ma，Renne et al., 1998).可以看出，年龄谱表明了Ar在FCs透长石颗粒中的分布是不均匀的，给不出有效的年龄坪(Phillips and Matchan, 2013)Fig.3 40Ar/39Ar step-heating spectra for two aliquots (FC3, FC4) of Fish Canyon Tuff sanidine‘Apparent’ ages have been calculated against an assumed age of 28.020Ma for FCT sanidine (Renne et al., 1998). These diagrams highlight distinct discordance in results and the lack of a statistical plateau segment(Phillips and Matchan, 2013)

2.3 40Ar/39Ar年代学标准样品研究现状

我们知道，40Ar/39Ar法年龄是一种“相对年龄”，它是以标准样品作为标尺进行对比而来。因此标准样品的“优劣”是决定40Ar/39Ar年龄是否“精准”的关键因素。优良的标准样品应该具有“新鲜的”、未受扰动的、K含量高、K和Ar分布均一的特性。 自然界中最易符合这些要求的是那些来自快速冷却的酸性或碱性岩浆岩中的矿物，其中以火山岩中的透长石最为理想，因为透长石快速冷却结晶而成、不易蚀变、K含量高、晶体结构稳定、K和Ar分布均一性好。尽管多年来应用于40Ar/39Ar年代学的各种各样的标准样品有30余个，通过过去几十年来的不断标定与实践，只有极少数几个标准样品被认为是“优良的”，在小样品或单颗粒级别均一，如上面讨论的FCs和年轻标样ACs(1.194±0.007Ma)，是目前最为广泛应用的两个标准样品，被普遍应用于激光单颗粒分析。

但实际上，正如我们前面的讨论，FCs标样的离散度为～1%左右。也就是说，即使使用目前最好的标准样品(FCs)的标定结果，其带来的误差或不准确度为～1%。对于100Ma的样品来说，标样带来的不准确度高达～1Ma。

由于标准样品最主要的功能是全熔年龄的可靠性与一致性，因此在前面的讨论中我们只关注了FCs的全熔结果(单颗粒或多颗粒)，其不同的标定值实际上反映了该标准样品的不均一性，因此有必要观察其颗粒内部的均一性。质谱技术的新进展使得我们可以看到更细微的东西，这由最近的研究中可以看出(Phillips and Matchan, 2013)。图3中的单颗粒激光阶段加热分析详细地解析了FCs矿物颗粒中Ar分布的不均匀性(40Ar/39Ar年代学中假定K的分布是均一的)。从图3中的两次平行分析的结果可以看出，这个“最好”的标样的年龄谱在27.85～28.20Ma之间单调上升，几乎没有稳定的年龄坪，其最外层(最小温度阶段)年龄可达28.5Ma，尽管其份额只占总释放气体的～2%(图3)。这表明，该标准样品矿物颗粒最外层曾受到低温扰动(蚀变)而含过剩40Ar，而其主要部分则从外至内放射性40Ar含量逐步升高。有三种情形可以造成这种情况：1)矿物外层有40Ar的丢失；2)样品中子活化时39Ar的反冲；3)矿物颗粒的核部有过剩40Ar。由于其最外层年龄值更高，表明最外层40Ar含量最高，因此可以排除蚀变造成40Ar丢失的可能性。中子活化时39Ar反冲是各向同性的，它能造成39Ar在核部的聚集和边部的丢失，使得矿物核部年龄偏低和边部年龄偏高，而从图3中看不到这种情况，因此第二种可能性也可以排除。造成这种年龄谱的最大可能性是核部含有高温阶段的过剩40Ar，这种过剩40Ar往往和高活化能的阴离子空穴的有关(McDougall and Harrison，1999)。

由此可见，缺少优良的标准样品目前仍是困扰40Ar/39Ar年代学的重要问题，均一性差的标样的数据离散是40Ar/39Ar最终年龄离散的重要来源，因此亟需研制新一代的、“优良的”标准样品。

3 封闭温度与热年代学

3.1 热年代学中的40Ar/39Ar法与U-Pb法

自从20世纪70年代Dondson (Dondson, 1979)年提出了封闭温度的概念以来，人们认识到了同位素年龄实际上是一种“冷却年龄”，即矿物温度下降到足以使其同位素体系封闭的温度以来的时间。在对岩浆岩年代学的研究过程中，很多文献中错误地认为40Ar/39Ar年龄是岩体的“冷却年龄”而U-Pb年龄是岩浆的“侵位年龄”。实际上，所有同位素均受热扩散作用的影响，年龄都代表“冷却年龄”，只是不同的同位素元素在热作用下的扩散速率不同，它们的封闭温度不一致，即开始计时的温度不同。通常，锆石的U-Pb同位素体系封闭温度高，开始计时的温度高达850～900℃左右(如McDougall and Harrison, 1999; Shenetal., 2012)，其年龄被很多人误认为是岩浆侵位的“绝对时间”。实际上，它只是相对于其它同位素年龄更接近岩浆侵位的时间而已。也就是说，岩浆在1000℃以上侵位到冷却至～900℃的时间，我们永远无法知道。

40Ar/39Ar法涉及稀有气体(Ar)的迁移扩散，同位素体系对温度的响应十分灵敏，且遵循气体扩散方程，这是40Ar/39Ar法可以定量模拟岩体热历史的基础。

图4给出了我们常用的不同同位素体系构建的温度-时间过程，即热历史。其中K-长石的封闭温度不像其他矿物一样是一个基本确定的值，而是一个连续的温度区间(约350～150℃，McDougall and Harrison, 1999，Loveraetal., 1989, 1991; Ingeretal., 1996)。考虑到岩体的侵位深度(如花岗岩一般为～30km)以及地温梯度(假定为～20℃/km)，由于岩体温度高于环境温度，则600℃以上热历史更多地反映了造山过程中侵入岩浆的原地热传导冷却，涉及U-Pb高温同位素体系；而600℃以下的热历史一般反映的是山体隆升-剥蚀-去顶的过程，涉及到40Ar/39Ar、FT(裂变径迹)、(U-Th)/He、Rb/Sr等中低温同位素体系。

图4 各种同位素体系形成的温度-时间热历史(据McDougall and Harrison, 1999; Shen et al., 2012)600℃以上的热历史更多地反映了造山过程中的岩浆过程；而600℃以下主要反映了岩体的抬升-剥蚀去顶过程Fig.4 Thermohistory toolkit (after McDougall and Harrison, 1999; Shen et al., 2012)The thermohistory over 600℃ reflect more the orogeny process, whilst that below 600℃ reflect more the uplift and erosion history

U-Pb法通常不能用于中低温(600℃以下)热历史研究，在高温段岩体易发生原地冷却，与构造隆升冷却难以区分，因此U-Pb法一般能不应用于构造热历史的恢复。同样，“叠加作用”是构造活动的一个重要特点，在诸如韧性剪切、伸展、挤压等过程中广泛存在。发生于地壳浅部的、后期叠加的构造作用过程中温度一般很难达到600℃以上，因此U-Pb法在这一方面的应用主要是提供原岩时代的手段，较难受到后期构造的重置。

绝大部分的地球构造作用发生于中上地壳内，涉及温度在～500℃以内，因此40Ar/39Ar法成为研究构造热历史的重要手段，并且由于Ar同位素的扩散和分布遵循扩散方程，其阶段升温的年龄谱记录了温度的变化过程，而温度的变化过程是构造过程的体现。因此原则上讲，40Ar/39Ar法年龄谱可以反映构造过程。但是实验过程中，由于角闪石、黑云母等含水矿物在阶段加热的高温阶段发生结构坍塌而失去了恢复Ar同位素分布特征的能力，难以用于热历史的反演。相反，K-长石不含水，在高温中结构稳定，可逐步释气而再现Ar同位素的分布特征。因此钾长石可以用于反演热历史，并追溯其构造演化过程。

3.2 多重扩散域(MDD)模型的问题与使用

K-长石的40Ar/39Ar年龄谱一般具有独特的、单调上升的特征，这是Ar同位素热扩散作用的体现，即和它经历的构造热过程相关，反应了～350℃到150℃的热历史(Loveraetal., 1989, 1991, 1993; Ingeretal., 1996；McDougall and Harrison，1999; Warthoetal., 1999; Casssata and Renne, 2013)。这是40Ar/39Ar年代学家的共识，这从20世纪90年代德国超深钻的工作可以得到直接的证明 (Reddyetal., 1999)。来自9000m深的钻孔底部的K-长石矿物的年龄谱从零单调上升至350Ma。据测量该深处的环境温度为265℃(Warnock and Zeitler, 1998)，介于350～150℃(K-长石封闭温度范围)之间。据MDD理论预测该样品的最小扩散域应该完全退火，年龄谱的最小年龄为零，而最大扩散域应不受影响而保持原来的年龄。实际的分析结果证实了这一推测(Warnock and Zeitler, 1998)，年龄谱的最小年龄为零，而最大年龄和白云母年龄(350Ma)一致，因为K-长石的最大封闭温度和白云母基本一致(350℃)。

对于K-长石年龄谱反映了它所经历的热历史这一点，大家毫不怀疑。但在如何提取、能否准确提取这种热历史，却分歧巨大。因此，关于可否、或如何揭示K长石记录的这种时间和温度关系的争论，持续了20多年。

虽然已认识到了Ar在钾长石中的扩散机制非常复杂且无法准确地定量描述，但Loveraetal. (1989, 1991, 1993)、Ingeretal. (1996 )还是依据Ar扩散的宏观观察提出了一个颇具新意的概念：多重扩散域。他们认为钾长石的的阶梯状年龄谱是赋存在这些不同扩散域中的Ar在阶段加热中由小到大逐步耗尽的表现；Ar在所有的扩散域中都服从“体积扩散”，这一假设是MDD模型的基础，因为只有满足这一假设，才能使用扩散方程来进行模拟计算。

而几乎同时，Lee(1995)提出了多路经(MP)模型，该模型认为，Ar在硅酸盐矿物中的扩散不总是遵从“体积扩散”，Ar的扩散是“多方式的”，并且它们之间还“相互干扰和反应”，这和K-长石中复杂的微结构所决定的。由于MP模型“考虑太多”，且“非体积扩散”无法定量描述，因此该模型始终是一个概念性模型而没有实际应用。而如果剔除了“非体积扩散”部分，MP和MDD没有实质区别。

尽管MP模型从没有过实际应用，但它却指出了MDD模型的理论缺陷，即Ar的扩散有一部分是不遵从“体积扩散”的快速扩散，这一部分Ar的分布是MDD无法描述的，或“错误”地描述了的。从那以后，基于微区矿物学研究的、关于Ar扩散的研究结果发现这些矿物学的结果和MDD预测的结果不一致。实际上，这些争论的核心就是Ar的扩散域的定义。

什么是Ar的扩散域？我们很自然地认为是矿物颗粒的大小。但在多重扩散域理论中扩散域并不是矿物颗粒的大小，因为随着矿物颗粒的减小，K-长石年龄谱的形态基本不变，因此Loveraetal. (1989, 1991, 1993)、Ingeretal. (1996 )认为Ar的扩散域不是一个物理概念，而是Ar的扩散机制，即不同的扩散域反映的是不同的扩散机制或途径，如空穴之间的扩散定义了某种扩散域，而分子间隙之间的扩散定义了另一种扩散域。显然，这样的扩散域不能被直接测定、难以观察、且是在分子层级上运作的。由于不能直接“看”到扩散域，加上Loveraetal. (1989, 1991, 1993)、Ingeretal. (1996 )对扩散域概念的描述模糊不清，引起了不少年代学家的质疑(Lee, 1993, 1995; Parsonsetal., 1999a, b; Warthoetal., 1999; Cassata and Renne, 2013)。如Lee(1993，1995)认为K-长石中总存在大量的、可供Ar扩散扩散的通道，这些通道的存在使得Ar的扩散不服从体积扩散，及Ar的扩散要比MDD模式描述的要快得多，因此实际Ar的分布和温度的关系并不像MDD所描述的那样。Warthoetal.(1999)采用激光剥蚀手段仔细研究了“宝石级”的马达加斯加K-长石中的Ar分布，认为不存在所谓的多扩散域，是“活化能”的变化造成了Ar扩散参数的变化。Parsons(Parsonsetal., 1999a, b)等从多项研究中得出结论，认为K-长石的台阶式上升年龄谱是复杂的微结构造成的，虽然和温度有关系，但远不是MDD所描述的那样。

归纳起来，对MDD的质疑主要集中在下面问题：1)低温下K-长石条纹化；2) 实验中1000℃以上造成的矿物均一化和无序化；3)隐条纹长石中39Ar的反冲影响；4)微孔等快速扩散通道的存在；5)反冲作用对晶格的损伤形成的扩散通道；6)退火作用造成的晶格损伤在低温下的愈合造成的Ar扩散系数变小；7)液体包裹体中可能的过剩Ar的影响；8)加热过程中矿物碎裂的影响；9)K-长石晶体结构中分子键的断裂以及Si、Al失序。这些矿物学研究和MDD模型结果的矛盾是人们对它质疑的主要原因。

我们必须承认，严格的矿物学研究揭示了及其复杂的K-长石显微结构图像，它们共同控制了Ar的扩散行为。可以肯定的是，必然还有更多的细节没有被发现，随着科学的进步，相信会有更多的控制Ar扩散机制被发现。而作为一个数学模型，MDD模式显然没有全面地、完整地、准确地描述这些可能控制Ar扩散的所有机制，实际上它也做不到这一点。否则MDD模型永远是一个概念性模式，就像“多路径”(MP)扩散模型，无法进入实际应用中。实际上，如果将MP模型简化到可应用的水平(如将其“扩散域之间会发生反应”的条件去掉)，它将和MDD模型基本没有区别(Arnaud and Kelley, 1997)。

关于MDD模型的讨论引出了一个重要的问题，这是我们在将复杂的自然过程定量化、模型化时都必须面对的问题：当我们定量化一个复杂的地质过程时，细节有多重要？就从Ar的扩散提取冷却历史来看，很多被矿物学研究观察到的、可能影响Ar扩散的机制并不能对最终的结果产生不可接受的、致命的影响，有些甚至可以完全忽略。如通过扩散及模拟研究表明(Loveraetal., 2002)，低温(200～300℃)重结晶作用并不能显著影响MDD冷却历史，也就是说，上面9个质疑中的1)，3)，6)，9)实际上对冷却历史没有重大的影响；而质疑2)的影响也无关紧要，因为K-长石的晶体结构主要在1200℃以上发生无序化。质疑7)，液体包裹体中的过剩Ar的一般在低温阶段就可以剔除(<～700℃)，此外，这种液体包裹体一般为此生包裹体，和Cl元素密切相关(McDougall and Harrison，1999)，因此可以通过38ArCl进行校正。由于高温阶段的过剩Ar无法校正，因此此类K-长石不能进行冷却历史研究。质疑4)、5)、8)实际上涉及到“体积扩散”的问题，研究(Casssata and Renn，2013)表明，Ar在长石中的扩散是各向同性的，至少在目前的条件下观察不到各向异性的扩散特征，我们可以理解为无论扩散域的大小，Ar在其中的扩散都是各向同性的，也即Ar的扩散遵从体积扩散。这对MDD而言非常重要。

图5 三个样品的背散射电子显微镜图像和它们的逐步升温39Ar和37Ar Arrhenius图(据Casssat and Renn, 2013)其中(a, b)为来自Alpine Verzasca Valley变质花岗岩的倍长石(Bytownite)；(c, d)为来自Stillwater复合岩体的倍长石；(e, f)为来自GrassValley的斜长岩.Alpine变质花岗岩中含有石英(Quartz)和碱性长石共生；Stillwater复合岩体的倍长石含有白云母(Muscovite)脉，并发育空隙；GrassValley斜长岩中发育白云母包体、富Na质长石蚀变、含Fe蚀变物.Arrhenius图表明这些样品的Ar扩散受制于蚀变界面、石英和斜长石以及碱性长石的共生面，表明次级扩散域的存在Fig.5 Ar Arrhenius plots for prograde heating and BSE images of (a, b) bytownite from a metamorphosed Alpine granitoid, (c, d) bytownite from the Stillwater Complex, and (e, f) anorthite from Grass Valley (after Casssat and Renn, 2013)The Alpine granitoid contains quartz sub-grains and alkali feldspar intergrowths. The Stillwater Complex bytownite contains veins of muscovite and porous, microcrystalline Na-rich feldspathic alteration. The Grass Valley anorthite contains large muscovite inclusions, plagioclase sub-grains, Na-rich feldspathic alteration, and Fe-rich alteration. The Arrhenius arrays obtained from these samples are sub-horizontal and consistent with alteration surfaces and incoherent subgrain boundary interfaces between quartz, plagioclase, and alkali feldspar defining diffusion domains

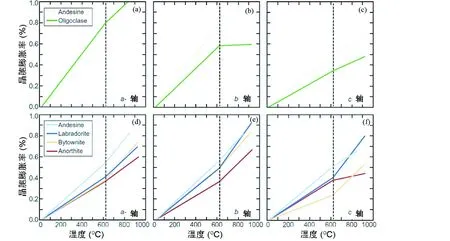
图6 斜长石在的热膨胀作用(据Casssat and Renn, 2013)高于600℃，富Na长石的热膨胀系数减小，而富Ca长石的热膨胀系数增大Fig.6 Linear regressions of plagioclase thermal expansion data acquired at temperatures above and below ～600℃ (after Casssat and Renn, 2013)Above ～600℃, thermal expansion coefficients decrease in Na-rich feldspars (a-c) and increase in Ca-rich feldspars (d-f)

详细的扩散研究(Casssata and Renn，2013)表明，K-长石中小于矿物颗粒的次级扩散域普遍存在，可由下面的这些微结构定义(图5)：后生的受应变控制的条纹、出溶条带、后期重结晶形成的蠕状结构等，它们和岩浆后期的作用有关(McLaren and Reddy，2008)，形成的次扩散域可以有效地作为多重扩散域应用于MDD模型(如图5a)。而受应力控制的裂隙、定向排列的各种界线(McLaren and Reddy，2008)、变质矿物、粘土矿物及溶解沉积物(Casssat and Renn，2013)、氧化物条带等和岩浆作用没有关系的微结构的出现，表明该样品不适合热历史的分析(如图5c，e)和。因此，进行热历史的分析首先要分析矿物的显微结构，一般意义的SEM图像分析就可以了(图5)。

Ar的扩散参数的确定还需考虑实验室高温分析中热作用造成的晶体结构膨胀和晶系转变(三斜晶系转变为单斜晶系)的影响(图6和图7)。热膨胀作用使得晶胞体积变大，大致发生在实验过程中的600℃左右(图6)，将导致Ar扩散的增强，使得计算的扩散系数偏高；而晶系转变大约发生在900～1000℃，可能导致K-长石Ar扩散减弱(图7)。遗憾的是现在还无法确定这一影响有多大，但模拟计算表明(Casssat and Renn，2013)，这一影响可能导致采用MDD计算的冷却历史在低温段虚高了50左右(图8)。这在解释冷却历史计算结果时要予以考虑。

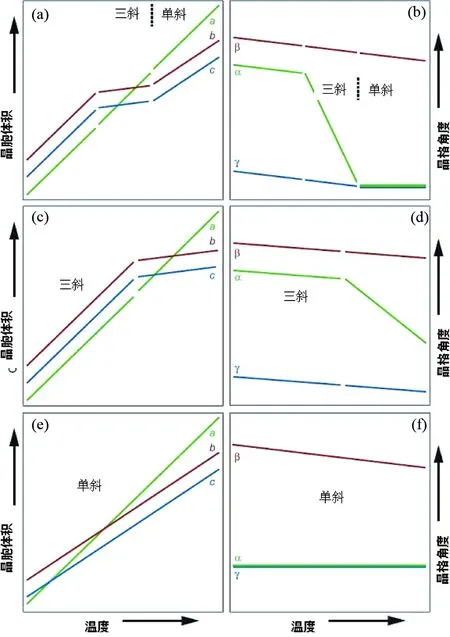
图7 热膨胀所用造成的晶胞体积变化、晶格角度变化和晶系转变(据Casssat and Renn, 2013)(a、b)-富钠长石在高温中由三斜转变为单斜晶系；(c、d)-富Na斜长石没有出现晶系转变；(e、f)-富K长石在所有阶段的温度中都保持了单斜晶系Fig.7 Schematic plots of the effects of thermal expansion on unit cell dimensions and angles in different minerals (after Casssat and Renn, 2013)(a, b)-Na-rich feldspars that undergo a triclinic to monoclinic transition at high-temperature; (c, d)-Na-rich plagioclase feldspars that do not undergo the aforementioned transition; (e, f)-K-rich feldspars that are monoclinic at all temperatures

从上面详细的扩散研究可以看出，MDD模型仍是解析地质热历史有力的工具，它的基本假设得到了论证。但在实际应用中，需要进行详细的矿物分析，和对热膨胀及可能的晶系转化作用的考虑。MDD模型是建立在对Ar扩散的宏观观察之上的，它不是描述矿物中Ar扩散的工具，而是描述Ar的宏观扩散和温度之间的关系。MDD不能预测微区扩散结果，可能表示它有偏差，也可能说明微区扩散结果并不是故事的全部，因为根本无法全面描述这些微结构的扩散特征，甚至可能还有控制Ar扩散的显微结构没有被发现。

3.3 压力对封闭温度的可能影响

迄今为止，40Ar/39Ar热年代学的各种理论在解释基底岩体的热历史中没有考虑压力的影响，这是因为早期的试验结果认为压力不影响Ar的扩散(如Dodson, 1979)。在Arrihenius关系式中，如果考虑了压力因素，其表达式就为

D=D0exp[(-E+PV)/RT]

(1)

而不是

D=D0exp[-E/RT]

(2)

其中D为扩散系数，D0为频率因子，E为活化能，P为压力，V为体积，R为气体常数，T为温度。

近来的实验研究表明，压力不但影响Ar的扩散系数，更重要的是还影响矿物的封闭温度。如Carroll (1991)发现，即使在较低的压力下(0.1～0.4GPa)正长石和钠长石玻璃中Ar的扩散系数也随压力的增大而明显减小；在中高压力下(0.5～2.0GPa)这一作用更加显著(陈道公等, 1992, 1994; Behrens and Zhang, 2001)，且温度越低压力的作用越明显(Behrens and Zhang, 2001)。压力对Ar在矿物中分布的的另一个重要影响是可能提高了矿物的封闭温度。高温高压试验研究表明，随着压力从0.5GPa上升到1.5GPa，黑云母的封闭温度在10℃/Ma的冷却速率下从450℃提高到540℃(陈道公等, 1992, 1994)，远远高于不考虑压力情况下的～350℃。

一些地质观察也证实了上述的实验结果。Maureletal. (2002)发现在来自法国Variscan高压造山带(变质温度600～700℃)的变质花岗岩中的黑云母仍保持着完整的原岩Ar同位素年龄，和U-Pb年龄一致，这与通常认识不同(一般认为黑云母Ar同位素体系封闭温度低而应在这次变质事件中归零)，表明压力使得该造山带中的黑云母中的Ar同位素体系在750℃时仍然保持封闭而得以保存原岩年龄，比公认的封闭温度值(～350℃)高了400℃。而Kelley and Wartho (2000) 观察到来自金伯利岩中上地幔(～1100℃)包体的金云母由于高压力仍然记录了包体的年龄，其封闭温度比正常值(350℃)高了～800℃，再次证明了压力对封闭温度的影响。在我国山西、山东出露的中生代金伯利岩中包体的金云母也观察到同样的现象，Ar/Ar年代学研究表明，这些金云母也保留了元古代古老地壳的年龄信息(Wangetal., 2014)。 这些现象表明，处于地壳基底的地质岩体，在暴露出地表的各种地质过程中遭受的压力影响了Ar的扩散、封闭与分布，因而必然影响到以此为基础的热年代学模拟，因此必然影响到对以热年代学为手段的地质过程的恢复。这种影响有多大，是否稳定，是否可以进行定量的实验研究，特别是记录了连续温度信息而被广泛应用的钾长石是否也遭受了压力的影响，须通过系统的试验研究加以揭示。如果反向思考，Ar的分布对压力的响应是否可以成为我们了解基底岩体剥露过程中所遭受压力信息的指示器？对此问题的探索，意义将十分深远。

4 两种不易发现的过剩Ar

40Ar/39Ar法也需扣除初始Ar与U-Pb法扣除“普通铅”类似，其比较独特的是初始Ar基本可以分为两种：一种是只含大气Ar的初始值，其40Ar/36Ar值为295.5±0.5；另一种是大气Ar和过剩Ar混和组成的初始值，其40Ar/36Ar值大于295.5。比值为大气Ar的初始值一般形成于地表或近地表的地质环境中，而过剩Ar则多形成于地球深部环境，因为在深部的岩石易于捕获周围不同于大气组成的Ar作为其初始值。在40Ar/39Ar年代学中，年龄谱给出的“坪年龄”是一种“模式年龄”，即“坪年龄”的获得需要假定矿物中Ar同位素的初始值为大气值，即295.5±0.5，数据处理时按此值扣除初始值。因此，如果样品中的初始值含有过剩Ar，坪年龄就会给出错误的结果，因为它仍然按大气值来扣除。这就需要在扣除初始值时将过剩Ar扣除。年代学中的等时线可以获得初始同位素比值，与之类似，40Ar/39Ar年代学中的“反等时线”也具有这样的功能。

但有两种情况“反等时线”却难以凑效，不能有效扣除或识别过剩Ar。一种是年轻火山岩样品(<1Ma)，另一种是高压环境中的地质样品。迄今为止，前者仍然没有被明确地认识到，而后者虽然被很多人意识到了，但其机理仍不被大多数人所认识。本节我们就来讨论这两种情况下的过剩Ar问题。

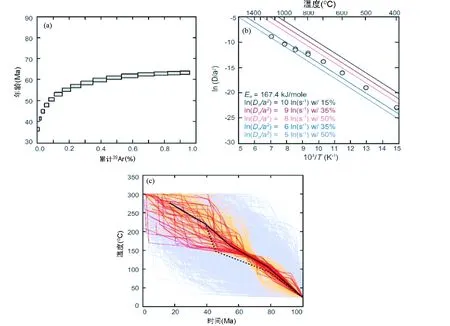
图8 碱性长石冷却历史模拟计算(据Casssat and Renne, 2013)(a)-假定的具有多重扩散域的碱性长石，包含有钠长石和正长石的条纹结构.假定其100Ma时侵入深度为20km的地壳中.(b)-计算的Ar Arrhenius 图解，显示了推算的扩散域的Arrhenius关系(黑线和蓝线)和真正的扩散域的Arrhenius 关系(黑线和红线).扩散域的ln(Do/a2)值和K百分含量列在左下角.真值和计算的值之间有差异，是由于在实验中扩散域由小到大逐步耗尽和热膨胀或结构转换共同造成的线性偏离.(c)-模使用推算的扩散域分布参数模拟的冷却历史.红线为那些能最佳拟合年龄谱的冷却历史(橘红为中等拟合，蓝线为拟合较差).可以看出，最佳拟合的平均冷却历史(黑实线)要比真值(黑虚线)温度更高Fig.8 An example of cooling history calculation for alkaine feldspar (after Casssat and Renne, 2013)(a)-hypothetical 40Ar/39Ar age spectrum obtained from a multiple-domain alkali feldspar comprising albite and orthoclase lamellae, intruded at 20km depth 100Ma ago and slowly uplifted to the surface. (b)-hypothetical Ar Arrhenius array (gray) obtained from this sample, shown alongside the inferred domain Arrhenius relationships [black and blue lines, with domain ln(Do/a2) values and percent of the total K contained therein listed in the lower, left corner] and true domain Arrhenius relationships (black and red lines, with Ar domain distribution parameters listed in the lower-left corner). Differences exist between the true (red) and inferred (blue) domain Arrhenius relationships because deviations from linearity arise during laboratory heating experiments due to both the exhaustion subgrain domains and structural transitions that occur upon heating. (c)-simulated thermal histories using the inferred (erroneous) domain distribution parameters. Thermal histories that best fit the target age spectrum are shown in red (orange=moderate fit; blue=poor fit). The inferred thermal history denoted by the black line (an average of the best fit solutions) is anomalously hot relative to the “true” solution (shown as a dashed black line)

4.1 年轻火山岩中的过剩Ar

由于凝结于地表，绝大部分火山岩的初始Ar都为大气组成而不含过剩Ar。但对于来源较深的玄武岩，特别是含有橄榄石斑晶的基性、超基性火山岩，则有可能含过剩Ar。在岩浆房中，首先结晶的橄榄石、辉石等斑晶(虽然已经结晶，但由于环境温度高，Ar同位素体系并不计时)，捕获周围环境中Ar进入其晶格中作为初始Ar，这种Ar其40Ar/36Ar比值不同于大气值，含过剩Ar。通常情况下，我们可以通过“反等时线”技术来扣除这种含过剩Ar的初始值。

图9 大同中更新世火山岩BB-24的年龄谱与反等时线图(据Wang et al., 2008)Fig.9 Age spectra and inverse-isochron of Datong basaltic BB-24 (after Wang et al., 2008)

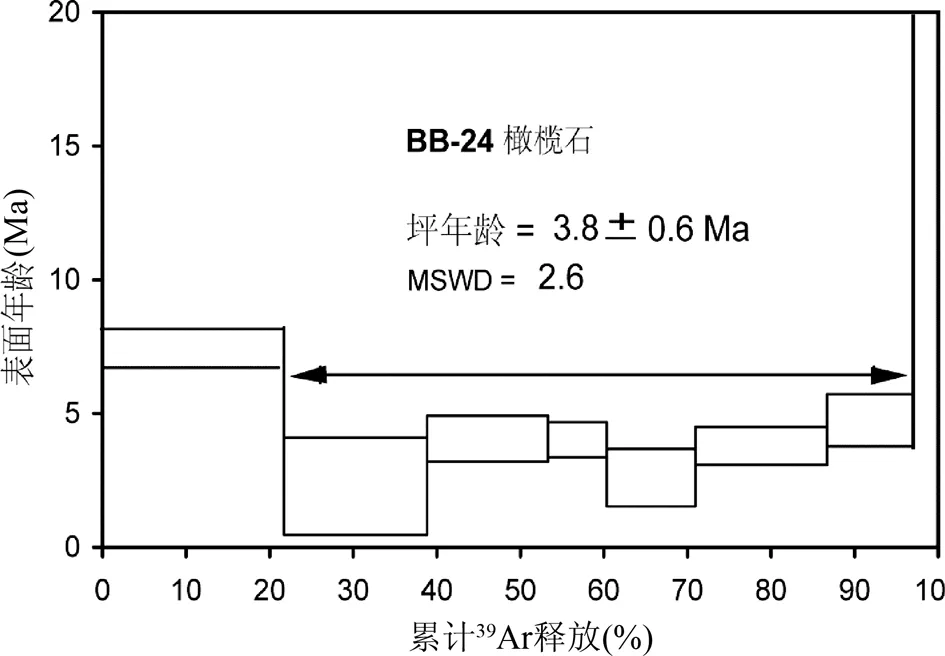
图10 由BB-24中分离出的橄榄石微晶年龄谱图 (据Wang et al., 2008)Fig.10 Age spectrum of olivine separates from BB-24(after Wang et al., 2008)

对于年轻火山岩来说，“反等时线”技术可能无法扣除过剩Ar。这可能是因为在年轻火山岩的初始Ar中，大气Ar占据绝对优势 (>95%) 而掩盖了可能存在的过剩Ar，使得反等时线无法识别出过剩Ar。样品越年轻，这种效应越明显。

对大同第四纪火山岩的研究充分论证了这一点。大同第四纪火山岩为橄榄玄武岩，前人已认识到其中含有过剩Ar (Chenetal., 1988)，但反等时线却指出其中不含过剩Ar(图9)。图9显示，大同玄武岩基质样品BB-24的反等时线年龄和坪年龄一致，初始值为296.5，和大气值吻合(Wangetal., 2008)。而从其中分离出的橄榄石微晶却给出了3.8Ma的坪年龄(图10)，充分表明了样品中含有过剩Ar。

图11对比了对该样品纯化前和纯化后的多次全熔分析结果，可以看出无论是40Ar的含量还是年龄值，纯化后的结果都大幅度降低并且趋于稳定，表明这种物理提纯可以有效地剔除过剩Ar的影响。

由上面的讨论可见，鉴于反等时线难以分辨和剔除年轻样品中的过剩Ar，使得我们在面对年轻样品时尤其要谨慎，不能轻易地依据反等时线来作出样品不含过剩Ar的判断。物理提纯法或许是唯一判断年轻样品中含有过剩Ar并剔除之的方法。尽管Renneetal. (1997)对造成庞贝城覆灭的维苏威火山大喷发时代的定年使得40Ar/39Ar法定年范围延伸至2000年以内(测定矿物为透长石)，并得到了普遍的认可。但其获得的反等时线却明确指出了该年轻样品含有过剩Ar，其初始值为306.9±1.3。这似乎和本节讨论的观点不一致。但Lanpheretal. (2007) 在后来对该喷发物(透长石)的定年中获得的反等时线却表明样品中不含过剩Ar，其初始Ar组成为296.8±3.0，基本为大气值。因此，对于维苏威火山AD 79年的喷发物中是否含有、或是否能通过反等时线来辨认出的过剩Ar，还有待进一步论证。

4.2 高压环境样品中的过剩Ar

相对于其他同位素体系，高压环境中样品的40Ar/39Ar年龄经常偏老，被认为是过剩Ar造成的结果(Lietal., 1994)，但从反等时线来看，一般很难发现高压环境中样品的过剩Ar (Sherlock and Arnaud, 1999)。例如Lietal. (1994)、Sherlock and Arnaud (1999)分别在研究中国大别超高压变质带和土耳其西北部Tavsanli高压变质带中的榴辉岩相时，发现其中的多硅白云母的40Ar/39Ar反等时线年龄比白云母的Rb-Sr年龄老得多，并且在反等时线图中40Ar/36Ar初始值基本为大气值，不含过剩Ar。由于Rb-Sr法在研究高压变质矿物年龄的可靠性已充分论证(如Ingeretal., 1996)，因此一般认为这是由于过剩Ar导致多硅白云母的40Ar/39Ar年龄偏老。但为什么通常用于判断过剩Ar的反等时线法在这种情况下失去了作用呢？为了了解这个问题，我们首先来看矿物在生成(岩浆结晶)或相变(变质作用)的过程中Ar的同位素组成及其变化。

图11 大同第四纪火山岩样品BB-24物理纯化前后对比(据Wang et al., 2008)无论是40Ar的含量还是年龄值，纯化后的结果都大幅度降低并且趋于稳定Fig.11 Comparison of analyses on aliquots of pre- and after-purification by hand-picking (after Wang et al., 2008)

正如上面所指出的那样，如果在矿物生成或相变的过程中(变质)其环境中没有过剩Ar，即其环境的40Ar和36Ar密切相关，比值为295.5(注意，36Ar只存在大气中，因此被看作大气Ar的代理指标)。而如果环境中含有过剩Ar，即其环境的40Ar仍然和36Ar密切相关，但比值大于295.5。这一部分的环境Ar在矿物生成或相变时进入而成为初始Ar。

在正常情况下(图12)，一般来说这些环境Ar进入矿物中能量要求不高的位置，如矿物的晶格缺陷、晶隙等位置中，因为它们没有足够的能量进入晶格中去。这些环境Ar就是初始Ar，它们的特点是在矿物中分布不均一，40Ar和36Ar密切相关。这一过程在矿物完全封闭时结束，此后位于矿物晶格上的40K衰变产生的40Ar开始积累，同位素时钟开始计时。这些放射性成因的40Ar位于矿物晶格上，其特点是在矿物中均匀分布，并且和40K密切相关。在反等时线图中，这些40Ar(包括大气40Ar、过剩40Ar、放射性成因40Ar)将以二元混合模式加以区分，区分的原则是和40K密切相关的40Ar为一个端元，和36Ar密切相关的40Ar为另一个端元。这就自然地将放射性成因40Ar和环境40Ar区分开来，前者给出矿物封闭以来的时间，后者给出初始Ar的组成。如果环境40Ar中含有过剩40Ar，将在初始Ar成分里被辨认出来。

图12 高压环境中过剩Ar可能形成的机制正常情况下， Ar进入矿物中能量要求不高的位置，如矿物的晶格缺陷、晶隙等位置中.而在高压环境下，矿物在生成或相变时，由于高压的作用，一部分环境Ar将获得高能量而进入矿物晶格中 (详见正文)Fig.12 Schematic plot of effect from high pressure upon Ar migrationIn normal case, Ar enters low-energy barrier postion, such as defects and interstitials; But under high pressure, Ar would enter the positions with high-energy barrier such as the lattice of the structure (see in text)

在高压环境下，情况可能不是这样的。矿物在生成或相变时，由于高压的作用，一部分环境Ar将获得高能量而进入矿物晶格中，这部分的环境Ar可能包含大气40Ar，也可能包含过剩40Ar。这些40Ar将和矿物封闭后40K衰变积累的放射性成因40Ar混合在一块，在矿物中均匀分布。另一种看法认为，在高压-超高压变质岩中，越是含钾高的矿物如多硅白云母其过剩氩的绝对含量越高，而石榴子石、辉石等微钾矿物虽然也含有过剩氩，但过剩氩的绝对量和多硅白云母相比少的多。这表明，这种情况下所谓的过剩氩实际上是矿物本身钾元素产生的放射性成因氩(而非环境氩)受高静压作用被圈闭在晶体内部形成的(图12)。

麻烦的是，在反等时线的二元混合图中，这些挤进矿物晶格中的过剩Ar将表现为和40K密切相关(而大气40Ar仍和36Ar相关，过剩40Ar将被分为两部分，一部分和36Ar组成大气成分(40Ar/36Ar=295.5)，另一部分将完全剩余(和36Ar相比)，独立存在，表现为和40K相关)。这样一来，在反等时线图中，初始端元为大气成分，不含过剩Ar；放射性成因40Ar端元由于混入了过剩40Ar而致使年龄变老。这一过程可由图12来形象地描述。

从上面的描述来看，压力可能使得环境Ar均匀地进入晶格位置中，或是原来的放射性成因Ar由于高压而圈闭在矿物晶格内而和K密切相关，致使反等时线无法区分该部分Ar。从定义上讲，对于新体系(新矿物)而言，这部分Ar不是过剩Ar而应划分为“继承Ar”，即“留在矿物晶格中的、继承了前期矿物时间特征的40Ar子体”。因此高压环境中的这种继承Ar，更多地反映了原岩的时间信息，具有一定的参考意义。对于一些形成时间短、折返速度快的高压造山带，更易产生这种现象(Sherlock and Kelley, 2002; Qiuetal., 2006; Scillet, 1996)。

5 结束语

基于对标准样品的标定和40K衰变常数的重新厘定，40Ar/39Ar法的精确度和准确度发展到了一个新的高度，达到甚至超过了U-Pb法。尽管准确度的进展落在了精确度的后面，但误差更小的定年结果对于判断数据的离散、确定时间序列具有重要意义。由于大气Ar成分占据绝对优势，完全掩盖了初始成分中可能存在的过剩Ar，使得反等时线难以辨别和剔除年轻火山岩中的过剩Ar，特别是在测定年轻玄武岩基质时，由于橄榄石微晶的存在，过剩Ar的影响不可忽视而必须加以剔除，采用物理纯化法是可能的剔除过剩Ar影响的唯一方法。高压环境中由于压力的作用，产生的继承Ar起到了过剩Ar的作用，造成变质矿物变老。这一老的年龄信息能够反映原岩的时间信息，具有一定的参考价值。压力对Ar同位素扩散的影响可能影响到了矿物的封闭温度，这对我们理解高压环境中的矿物的Ar同位素性质、岩体热历史的研究具有重要意义。实际上，压力不仅仅影响了Ar同位素体系，还可能影响了其他的同位素体系，如Rb-Sr体系等。如何研究压力的影响，其影响到底有多大，和封闭温度是什么样的关系，这一系列的问题需要我们深入的思考。K-长石的年龄谱可以反映岩体所经历的热历史，这从超深钻样品得到了直接的证实。建立在其上的多重扩散域模式从数学角度模拟了这一过程。该模型对不是描述Ar扩散机制工具，而是反映Ar扩散与温度宏观关系的手段。

致谢感谢两位审稿人富有建设性的意见，基于他们的意见之上的修改使得本文更加完善。

Cassata WS and Renne PR. 2013. Systematic variations of argon diffusion in feldspars and implications for thermochronometry. Geochim. Cosmochim. Acta, 112: 251-287

Arnaud NO and Kelley SP. 1997. Argon behaviour in gem-quality orthoclase from Madagascar: Experiments and some consequences geochronology. Geochim. Cosmochim. Acta, 61(15): 3227-3255

Behrens H and Zhang YX. 2001. Ar diffusion in hydrous silicic melts: Implications for volatile diffusion mechanisms and fractionation. Earth and Planetary Science Letters, 192(3): 363-376

Carroll MR. 1991. Diffusion of Ar in rhyolite, orthoclase and albite composition glasses. Earth and Planetary Science Letters, 103(1-4): 156-168

Cebula GT, Kunk MJ, Mehnert HH, Naeser CW, Obradovich JD and Sutter JF. 1986. The Fish Canyon Tuff, a potential standard for the40Ar/39Ar and fission-track dating methods. Terra Cognita, 6: 139-140

Chen DG, Jia MM, Pu ZP and Xie HS. 1992. Preliminery study on argon diffusion in biotite under high pressure and temperature. Chinese Science Bulletin, 37(2): 154-156 (in Chinese)

Chen DG, Jia MM, Li XB, Lu QM, Xie HS and Hou W. 1994. Argon diffusion in biotite under high pressure and temperature. Science in China (Series D), 24(2): 194-201 (in Chinese)

Chen W, Flisch M and Hurford AJ. 1988. BB-24: Re-collection of a Quaternary age standard for K-Ar dating. An Abstract, International Symposium, Time Scale Calibration, IGCP Project 196, Besancon, France, 50

Condomines M, Gauthier PJ and Sigmarsson G. 2003. Timescales of magma chamber processes and dating of young volcanic rocks. Rev. Mineral. Geochem., 52(1): 125-174

Dazé A, Lee JKW and Villeneuve M. 2003. An intercalibration study of the Fish Canyon sanidine and biotite40Ar/39Ar standards and some comments on the age of the Fish Canyon Tuff. Chemical Geology, 199(1-2): 111-127

Dodson MH. 1979. Theory of cooling ages. In: Jäger E and Hunziger JC (eds.). Lectures in Isotope Geology. Berlin: Springer, 194-202

Hurford AJ and Hammerschmidt K. 1985.40Ar/39Ar and K/Ar Dating of the Bishop and Fish Canyon Tuffs: Calibration ages for fission-track dating standards. Chem. Geol., 58(1-2): 23-32

Inger S, Ramsbotham W, Cliff RA and Rex DC. 1996. Metamorphic evolution of the Sesia-Lanzo Zone, Western Alps: Time constraints from multi-system geochronology. Contrib. Mineral. Petrol., 126(1-2): 152-168

Jourdan F and Renne PR. 2007. Age calibration of the Fish Canyon sanidine40Ar/39Ar dating standard using primary K-Ar standards. Geochimica et Cosmochimica Acta, 71(2): 387-402

Kelley SP and Wartho JA. 2000. Rapid kimberlite ascent and the significance of Ar-Ar ages in xenolith phlogopites. Science, 289(5479): 609-611

Kuiper KF, Deino A, Hilgen FJ, Krijgsman W, Renne PR and Wijbrans JR. 2008. Synchronizing rock clocks of Earth history. Science, 320(5875): 500-504

Lanphere MA and Baadsgaard H. 1997. The Fish Canyon Tuff: A standard for geochronology. EOS Trans. Am. Geophys. U., 78: S326

Lanphere MA and Baadsgaard H. 2001. Precise K-Ar,40Ar/39Ar, Rb-Sr and U/Pb mineral ages from the 27.5Ma Fish Canyon Tuff reference standard. Chem. Geol., 175(3): 653-671

Lanphere MA, Champion D, Melluso L, Morra V, Perrotta A, Scarpati C, Tedesco D and Calvert A. 2007.40Ar/39Ar ages of the AD 79 eruption of Vesuvius, Italy. Bull. Volcanol., 69(3): 259-263

Lee JKW. 1993. The argon release mechanisms of hornblende in Vacuo. Chem. Geol., 106(1-2): 133-170

Lee JKW. 1995. Multipath diffusion in geochronology. Contrib. Mineral. Petrol., 120(1): 60-82

Li SG, Wang SS, Chen YH, Liu DL, Qiu J, Zhou HX and Zhang ZM. 1994. Excess Argon in phengite from eclogite: Evidence from dating of eclogite minerals by Sm-Nd, Rb-Sr and40Ar/39Ar methods. Chem. Geol., 112(3-4): 343-350

Lovera OM, Richter FM and Harrison TM. 1989. The40Ar/39Ar thermochronometry for slowly cooled samples having a distribution of diffusion domain sizes. Journal of Geophysical Research, 94(B12): 17917-17935

Lovera OM, Richter FM and Harrison TM. 1991. Diffusion domains determined by39Ar released during step heating. Journal of Geophysical Research, 96(B2): 2057-2069

Lovera OM, Heizler MT and Harrison TM. 1993. Argon diffusion domains in K-feldspar II: Kinetic properties of MH-10. Contrib. Mineral. Petrol., 113(3): 381-393

Lovera OM, Grove M and Harrison TM. 2002. Systematic analysis of K-feldspar40Ar/39Ar step heating results II: Relevance of laboratory argon diffusion properties to nature. Geochimica et Cosmochimica Acta, 66(7): 1237-1255

Maurel O, Monie P, Respaut JP, Leyreloup AF and Maluski H. 2003. Pre-metamrophic40Ar/39Ar and U-Pb ages in HP metagranitoids from the Hercynian belt (France). Chemical Geology, 193(3-4): 195-214

McDougall I and Harrison TM. 1999. Geochronology and Thermochronology by the40Ar/39Ar Method. New York: Oxford Univ. Press, 199-204

McLaren S and Reddy SM. 2008. Automated mapping of Kfeldspar by electron backscatter diffraction and application to40Ar/39Ar dating. J. Struct. Geol., 30(10): 1229-1241

Min K, Mundil R, Renne PR and Ludwig KR. 2000. A test for systematic errors in40Ar/39Ar geochronology through comparison with U/Pb analysis of a 1.1Ga rhyolite. Geochim. Cosmochim. Acta, 64(1): 73-98

Oberli F, Fischer H and Meier M. 1990. High-resolution238U-206Pb zircon dating of Tertiary bentonites and Fish Canyon Tuff: A test for age ‘‘concordance’’ by single crystal analysis. In: Proceedings of the 7thInt. Conf. Geochron. Cosmochron. Isot. Geol. Geol. Soc. Aust. Abstr., 27: 74

Parsons I, Rex DC and Guise P. 1999a. Ar-loss by alkali feldspar. Geochim. Cosmochim. Acta, 52: 1097-1112

Parsons I, Brown BL and Smith JV. 1999b.40Ar/39Arthermocronology using alkali feldspar; real thermal history or mathematical mirage of microtexture? Contrib. Mineral. Petrol., 136(1-2): 92-110

Phillips D and Matchan EL. 2013. Ultra-high precision40Ar/39Ar ages for Fish Canyon Tuff and Alder Creek rhyolite sanidine: New dating standards required? Geochimica et Cosmochimica Acta, 121: 229-239, doi: 10.1016/j.gca.2013.07.003

Qiu HN and Wijbrans JR. 2006. Paleozoic ages and excess40Ar in garnets from the Bixiling eclogite in Dabieshan, China: New insights from40Ar/39Ar dating by stepwise crushing. Geochimica et Cosmochimica Acta, 70(9): 2354-2370

Reddy SM, Potts GJ and Kelley SP. 1999. The effects of deformation-induced microstructures on intragrain40Ar/39Ar ages in potassium feldspar. Geology, 27(4): 363-366

Renne PR, Deino AL, Walter RC, Turrin BD, Swisher CC, Becker TA, Curtis GA, Sharp WD and Jaouni AR. 1994. Intercalibration of astronomical and radioisotopic time. Geology, 22(9): 783-786

Renne PR, Sharp WD, Deino AL, Orsi G and Civetta L. 1997.40Ar/39Ar dating into the historical realm: Calibration against Pliny the younger. Science, 277(5330): 1279-1280

Renne PR. 1998. Intercalibration of standards and other sources of error in Ar/Ar dating. Geol. Assoc. Can. Min. Assoc. Can. Abstr., 23: A154

Renne PR and Min K. 1998.40Ar/39Ar dating of the 79 AD eruption of Vesuvius: An ab initio basis for improved accuracy in40Ar/39Ar geochronology. Min. Mag., 62(2): 1255-1256

Renne PR, Swisher CC, Deino AL, Karner DB, Owens TL and DePaolo DJ. 1998. Intercalibration of standards, absolute ages and uncertainties in40Ar/39Ar dating. Chem. Geol., 145(1-2): 117-152

Renne PR, Ludwig KR and Karner DB. 2000. Progress and challenges in geochronology. Science Progress, 83(Pt 1): 107-121

Renne PR, Mundil R, Balco G, Min K and Ludwig KR. 2010. Joint determination of40K decay constants and40Ar*/40K for the Fish Canyon sanidine standard, and improved accuracy for40Ar/39Ar geochronology. Geochimica et Cosmochimica Acta, 74(18): 5349-5367

Scaillet S. 1996. Excess40Ar transport scale and mechanism in high-pressure phengites: A case study from an eclogitized metabasite of the Dora-Maira nappe, western Alps. Geochimica et Cosmochimica Acta, 60(6): 1075-1090

Schmitz MD and Bowring SA. 2001. U-Pb zircon and titanite systematics of the Fish Canyon Tuff: An assessment of high-precision U-Pb geochronology and its application to young volcanic rocks. Geochim. Cosmochim. Acta, 65(15): 2571-2587

Shen C, Donelick RA, O’Sullivan PB, Jonckheere R, Yang Z, Miu X and Ge X. 2012. Provenance and hinterland exhumation from LA-ICP-MS zircon U-Pb and fission-track double dating of Cretaceous sediments in the Jianghan Basin, Yangtze block, central China. Sedimentary Geology, 281: 194-207

Sherlock SC and Arnaud NO. 1999. Flat plateau and impossible isochrons: Apparent40Ar/39Ar geochronology in a high-pressure terrain. Geochim. Cosmochim. Acta, 63(18): 2835-2838

Sherlock S and Kelley S. 2002. Excess argon evolution in HP-LT rocks: A UVLAMP study of phengite and K-free minerals, NW Turkey. Chemical Geology, 182(2-4): 619-636

Spell TL and McDougall I. 2003. Characterization and calibration of40Ar/39Ar dating standards. Chem. Geol., 198(3-4): 189-211

Steiger RH and Jager E. 1977. Subcommission on geochronology: Convention on the use of decay constants in geo- and cosmochronology. Earth and Planetary Science Letters, 36: 359-362

Steven TA, Mehnert HH and Obradovich JD. 1967. Age of volcanic activity in the San Juan Mountains. Colorado. Prof. Pap. Geol. Surv. (U. S.), 575D: D47-D55

Villeneuve M, Sandeman H and Davis WJ. 2000. A method for intercalibration of U-Th-Pb and40Ar-39Ar ages in the Phanerozoic. Geochim. Cosmochim. Acta, 64(23): 4017-4030

Wang F, Zhu RX, Yang L, He H and Lo C. 2008.40Ar/39Ar analyses on Quaternary K-Ar standard BB-24: Evaluations. International Journal of Mass Spectrometry, 270(1-2): 16-22

Wang F, Shi WB, Wu L, Feng HL, Zhang WB and Yang LK. 2014. Denudation and uplift of the basement of North China Craton: Constraints from40Ar/39Ar thermochronology. In preparation

Warnock AC and Zeitler PK. 1998.40Ar/39Ar thermochronometry of K-feldspar from the KTB borehole, Germany. Earth and Planetary Science Letters, 158(1-2): 67-79

Wartho JA, Kelley SP, Brooker RA, Carroll MR, Villa IM and Lee MR. 1999. Direct measurement of Ar diffusion profiles in a gem-quality Madagascar K-feldspar using the ultra-violet laser ablation microprobe (UVLAMP). Earth Planet. Sci. Lett., 170(1-2): 141-153

附中文参考文献

陈道公, 贾命命, 蒲志平, 谢鸿森. 1992. 高温高压下黑云母中氩扩散实验初步研究. 科学通报, 37(2): 154-156

陈道公, 贾命命, 李彬贤, 陆全明, 谢鸿森, 侯渭. 1994. 高温高压下黑云母中氩扩散研究. 中国科学(D辑), 24(2): 194-201