一种基于Petri 网的多目标无死锁蚁群调度算法

惠晓龙，郜振鑫

资源受限的项目调度问题(Resource Constrained Project Scheduling Problem，RCPSP)属于NP－hard 问题;广泛存在于制造系统等调度问题，它通过合理地分配资源，达到项目执行工期最短等优化目标［1］。在合理分配资源的过程中，死锁是一个重要的研究课题，目前人们从控制的角度提出了多种死锁避免控制策略，但是这些策略无法优化系统的运行性能，因此系统的无死锁优化调度是一个值得研究的问题［2－5］。传统的优化调度只有一个优化目标，而在实际项目中往往存在多个优化调度目标。

本文针对制造系统的赋时Petri 网模型，研究以总工期最短和紧急项目工期最短为优化目标的无死锁调度问题，建立系统的多目标无死锁蚁群调度算法。蚁群算法采用最大最小蚂蚁系统，通过修改状态转移概率公式，并给出算法最优解的评价函数，使蚂蚁综合多个优化目标选择路径。单只蚂蚁选择下一步可执行的操作时，进行死锁判断，将死锁避免控制策略嵌入到算法，实现无死锁调度。仿真结果验证了本文提出的多目标无死锁蚁群调度算法的可行性和有效性。

1 系统的Petri 网模型

Petri 网［2］结构是一个三元组N=(P，T，F)，其中P和T 都是有限但互不相交的集合。P 是位置(Place)的集合，T 是变迁(Transition)的集合，F⊆(P×T)∪(T×P)是有向弧(Arc)的集合。

Petri 网N 的一个标识或状态是一个映射M∶P→Z+，其中Z+={0，1，2，…}。给定标记Petri 网N=(P，T，F，M0)，用T*表示T 的所有变迁序列的集合，∀a=t0，t1，t2，…，tn∈T*，如果Miti＞Mi+1，i=0，1，2，…，n，则称a 为在M0下的可行序列，称Mi(i=1，2，…，n+1)为从M0的可达标识或状态。Petri 网N 中的一条路径是一个序列αuv=(u=x1，x2，…，xk+1=v)，其中xi∈P∪T，(xi，xi+1)∈F，i=1，…，k，k 是α 的长度。

本文采用位置赋时Petri 网模拟系统的特征，模型中一个标记必须在位置中经过一定时延，记作d(p)，才能进入下一个位置。

采用文献［2，4］给出的制造系统模型，如图1 所示。系统中有4 类机器(m1，m2，m3和m4)和3 类机器人(r1，r2和r3)，把资源集合表示为r={m1，m2，m3，m4，r1，r2，r3}，C(mi)=2，i=1，2，3，4，C(ri)=1，i=1，2，3。系统需要加工处理3 类工件，加工q1类工件的资源顺序是r2m2r2，加工q3类工件的资源顺序是r3m4r2m3r1，加工q2类工件有两条路径，其资源顺序分别是r1m1r2m2r3和r1m3r2m4r3。tij和pij中的字母i 代表第i 条路径，q1类工件的加工路径为p1st11p11t12p12t13p13t14p1e，q2类工件的加工路径有两条分别为p2st21p21t22p22t23p23t24p24t25p25t26p2e和p2st21p21t32p32t33p33t34p34t35p25t26p2e，q3类工件的加工路径为p4st41p41t42p42t43p43t44p44t45p45t46p4e。3 类工件需要加工的个数分别为8，12 和8。

图1 系统的Petri 网模型

2 多目标无死锁蚁群调度算法

2.1 算法简介

本文的蚁群算法采用最大最小蚂蚁系统(Max－Min Ant System，MMAS)，其主要思想是:仅更新每一代中最好的蚂蚁个体所走的路径上的信息量，加快收敛速度;并将各条路径上的信息量限制在区间［τmin，τmax］内，避免某条路径上的信息量远大于其他路径上的信息量，使蚂蚁的搜索行为集中到同一条路径上［6］。

针对制造系统的调度模型提出蚁群算法的数学模型，问题描述如下:针对一个可标识的自动制造系统(N，M0)，加工完一定任务的工件总共需要的操作数目为，所有加工操作的集合表示为{O1，O2，…，On}，操作Oi的加工时间为t(Oi)(i=1，2，…，n)，算法的任务就是寻找一个有序的加工路径或者操作序列，完成所有的加工任务，优化目标使系统的加工时间和紧急工件的加工完成时间最短。算法对系统的工件、资源和操作均按顺序采用10 进制进行编码。

2.2 多目标无死锁蚁群调度算法

算法中蚁群数量为m，蚂蚁k(k=1，2，…，m)在选择下一步操作时，根据文献［5］中提出的具有多项式复杂性的死锁避免控制策略(DAP)，将不会造成死锁的操作放入集合allowedk中，并从中选择下一步遍历操作，从而实现无死锁调度。在遍历的过程中，根据各操作之间遗留的信息素来决定下一个操作，同时考虑操作的启发式信息和紧急工件的优先级信息。Pkij表示第k 只蚂蚁由操作Oi转移到操作Oj的状态转移概率，由式(1)确定

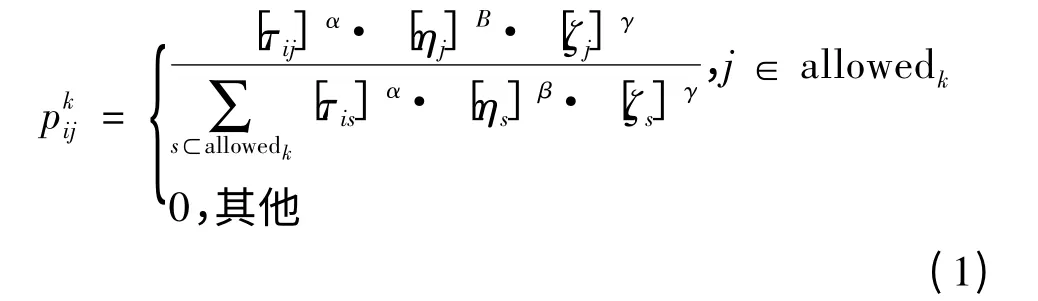
其中，τij表示操作Oi和Oj之间的信息素，初始时刻为常数;ηj表示在搜索过程中选择操作Oj的期望值，根据先验知识可知，本文ηj为操作Oj的最早开始加工时间的导数;ζj表示操作Oj对应工件的优先级，初始给定为常数。

α 表示信息素启发式因子，反映的是蚁群在遍历过程中所残留信息素的相对重要程度;β 表示期望启发式因子，反映了对下一个遍历操作所期望的相对重要程度;γ 表示优先级启发式因子，反映优先级的相对重要程度。如式(1)所示，蚂蚁优先选择信息素浓度高、能最早开始加工并且优先级高的操作路径。

算法每一次迭代只更新最优解路径上的信息素，因此给出了评价最优解的函数。假设系统中只含有一类紧急工件，其他工件都是普通工件，用式(2)的大小作为评价最优解α 的标准，其中ω1和ω2分别是系统加工时间t1和紧急工件加工时间t2的权值。ζ 表示紧急工件的优先级，finishtime 表示紧急工件的加工完成时间。

为防止算法过早收敛陷入局部最优解，当算法收敛时重置信息素模型，重启调度。用收敛因子cf描述算法的收敛程度;在初始时刻cf=0，当所有的信息素的值都等于τmax或τmin时，cf=1.0，由式(3)求得。

算法实现步骤:(1)系统初始化。蚁群中蚂蚁的总数，最大循环迭代次数，信息素初始化τij=0.5。(2)单只蚂蚁调度。首先根据死锁避免控制策略，保证每只蚂蚁在选择下一个操作之前，保证操作不会造成死锁，然后根据状态转移概率公式选择下一步操作，直到遍历完所有操作。(3)所有蚂蚁遍历完形成路径集合，从中选择最优路径更新信息素模型。(4)计算收敛因子，如果算法收敛后，重置信息素模型。(5)判断是否满足结束条件，即达到最大循环迭代次数，如果满足，则输出算法计算结果，算法结束。

3 算法仿真与结果分析

对图1 所示的制造系统的调度问题，采用蚁群算法对其进行调度，采用文献［7］中给出的加工时间数据，加工时间如表1 所示。

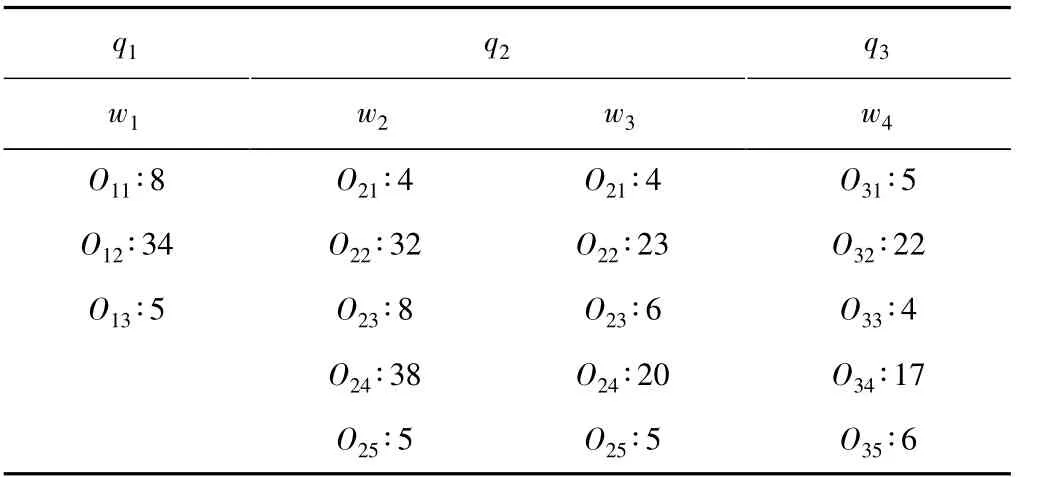
表1 制造系统操作加工时间

系统仿真参数设置如下。q1，q2，q3这3 类工件的优先级分别为(1，2，1)，q2类工件为紧急工件，α=3，β=3，γ=1，ρ=0.01，蚁群数量为10，迭代次数800，ω1=0.4，ω2=0.6。图2 是迭代最优解变化情况，图3是多目标全局最优解的的变化情况，求得所有工件完成时间428，紧急工件完成时间259，对应的最优调度路径为(t11，t21，t41，t32，t21，t22，t42，t21，t41，t12，t22，t13，t14，t43，t21，t42，t33，t23，t22，t34，t41，t21，t24，t23，t24，t22，t44，t21，t32，t45，t46，t21，t43，t44，t42，t25，t26，t35，t26，t11，t33，t32，t12，t25，t26，t45，t46，t43，t44，t34，t33，t21，t35，t26，t32，t13，t14，t21，t41，t34，t23，t22，t21，t24，t42，t35，t26，t23，t33，t41，t32，t24，t34，t21，t22，t45，t46，t43，t44，t21，t42，t35，t26，t33，t34，t32，t45，t46，t43，t25，t26，t23，t25，t26，t24，t23，t35，t26，t33，t24，t25，t26，t11，t44，t34，t41，t12，t42，t25，t26，t35，t26，t41，t11，t12，t42，t13，t14，t41，t11，t12，t13，t14，t13，t14，t11，t12，t11，t12，t43，t44，t45，t46，t42，t43，t44，t45，t46，t43，t44，t45，t46，t45，t46，t13，t14，t11，t12，t13，t14，t13，t14)。

图2 蚁群算法迭代最优解

图3 蚁群算法多目标调度最优解

从仿真结果可以看出，蚁群算法在迭代次数为约360 和705 时收敛，重置信息素模型重启调度，以免算法陷入局部最优解。算法根据优化目标权值的不同，做出权衡，选择最优解，从图中可以看出，算法较好地给出了调度的最优解，是可行、有效的。

4 结束语

本文针对资源受限项目中的制造系统调度问题，采用其Petri 网模型，将死锁避免控制策略嵌入到蚁群算法中，解决系统具有多个加工优化目标的问题，给出系统的多目标无死锁蚁群调度算法。蚁群算法采用最大最小蚂蚁系统，通过修改状态转移概率公式，使蚂蚁具有较大的概率优先选择紧急工件的加工操作，算法每次只更新最优调度解对应的信息素，给出评价函数来评价调度解的优劣。通过仿真实例，证明了算法的可行性和有效性。

［1］ 庞南生，孟俊姣.多目标资源受限项目鲁棒调度研究［J］.运筹与管理，2012(3):27－32.

［2］ EZPELETA J，COLOM J M，MARTINEZ J.A petri net based deadlock prevention policy for flexible manufacturing systems［J］.IEEE Transactions on Robotics and Automation，1995，11(2):173－184.

［3］ REVELIOTIS S A，LAWLEY M A，FERREIRA P M.Polynomial－complexity deadlock avoidance policies for sequential resource allocation systems［J］.IEEE Transactions on Automatic Control，1997，42(10):1344－1357.

［4］ XING K Y，ZHOU M C，LIU H X，et al.Optimal petri－net－based polynomial－complexity deadlock－avoidance policies for automated manufacturing systems［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A:Systems and Humans，2009，39(1):188－199.

［5］ 邢科义，田锋，杨小军，等.具有多项式时间复杂性的避免制造系统死锁控制策略［J］.自动化学报，2007，33(8):893－896.

［6］ STÜTZLE T，HOOS H H.Max－min ant system［J］.Future Generation Computer Systems，2000，16(9):889－914.

［7］ XING K Y，HAN L B，ZHOU M C.Deadlock－free genetic scheduling algorithm for automated manufacturing systems based on deadlock control policy［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2012，42(3):603－615.