基于Kalman滤波器的车式移动机器人跟踪方法

张香竹，余辉荣，汪俊彬

（华南理工大学 自动化科学与工程学院控制与优化中心，广州 510641）

目前，在智能监控领域，对视频序列中的多移动机器人进行实时跟踪已成为研究热点[1-2]。跟踪过程分为两种基本策略：一种是对机器人建立模型，并通过模型进行算法的应用；另一种则是不建立模型，如文献[3]中提出的直接利用反馈信息对机器人进行控制，但这种控制方式对于需要知道车头方向的车式移动机器人并不适用。文献[4]建立了非线性的机器人模型，虽然模型的精度较高，但是不适用于计算机控制。文献[5]中给出的机器人模型适用于轮式机器人，却不适用于车式机器人。Kalman滤波算法[6]、Condensation算法[7]等数学算法经常用于目标跟踪过程。由于Condensation算法实时性较差且动态模型精度较低，故很少使用。Kalman滤波是在已知系统和量测的数学模型、量测噪声统计特性及系统状态初值的情况下，利用输出信号的量测数据和系统模型方程，实时获得系统状态变量和输入信号的最优估计。Kalman滤波器不仅能对目标轨迹进行滤波和优化，还可以对目标状态进行预估[8]，且实时性较好，适用于多目标跟踪。

Kalman滤波器需使用线性化模型[9]，为了便于引入Kalman滤波器，本文首先对车式移动机器人进行建模，再利用线性化方法进行线性化和离散化，最后将多Kalman滤波器应用于多机器人的轨迹跟踪优化。

1 实验平台

实验平台硬件结构如图1所示。系统在逻辑层面上可划分为监控层、通信层和对象层。从实体结构分析，监控层包括上位机和摄像机，两者由IEEE1394接口连接。其中摄像机负责感知并收集图像帧、信息预处理、目标分割和目标定位等序列任务，最终完成监控区域内移动目标的坐标状态提取和实时监控工作；而上位机负责对摄像机的采样数据进行信息融合，通过对目标模型的建立及Kalman滤波器的运用，获得目标对象的多维状态，并实时显示于屏幕，为对象进一步的精确控制提供参考信息。通信层包含基站和无线射频RF（radio frequency）模块，其中基站负责整个系统运行的时间资源分配，规定系统内各通信单元的工作时隙，保证通信过程有条不紊地进行。无线射频模块的任务是通过空中接口实现基站与移动机器人之间的无线通信。对象层由多个被控对象，即多台车式移动机器人组成。被控对象和基站均采用ST公司的STM32系列32位芯片作为主控制器，提高系统总体通用性的同时也便于后续扩展。

图1 实验平台结构图Fig.1 Configuration of experimental platform

为了更直观地体现系统各部分之间的联系，给出系统框图如图2所示。本文选用积分分离PID控制器[10]，既能保证控制的实时性，又能减小稳态误差，保证控制精度。反馈环节包括上述的监控系统以及Kalman滤波器。其中监控系统的采样数据作为原始观测信息，而Kalman滤波器则根据机器人模型，对该观测信息和PID控制器输出的控制信号作进一步滤波和优化，并反馈给控制器，以输出作用于被控对象。

图2 系统框图Fig.2 System block diagram

该算法可以很好地实现对机器人的速度控制，使机器人在给定速度下平稳的运动。

2 具体实现

2.1 车式移动机器人建模

运用Kalman滤波器的前提是已知被控对象的线性化模型。本文所采用的被控对象是四轮车式移动机器人，其中两个后轮依靠直流电机提供前进动力，即为驱动轮，驱动方向与机器人前进方向一致；两个前轮通过舵机控制机器人的转向，即为转向轮。车式机器人的模型如图3所示。

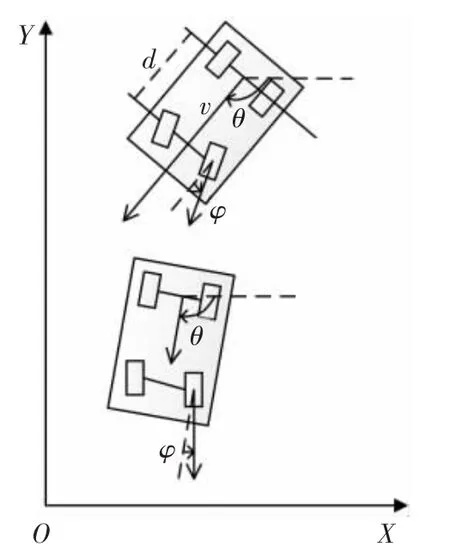
图3 车式移动机器人模型图Fig.3 Model of car-type mobile robot

根据四轮移动机器人的运动学模型

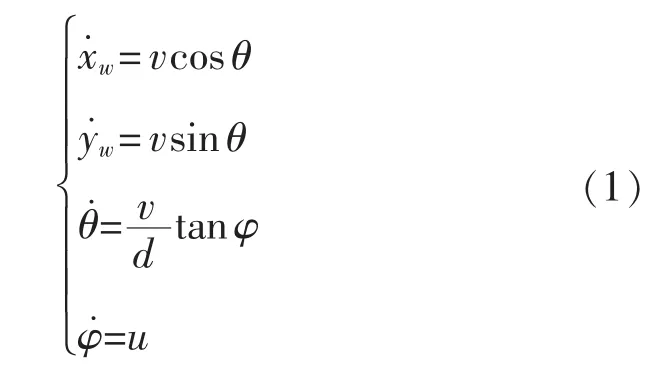
式中：（xw，yw）为机器人中心的世界坐标；θ为航向角即机器人车身方向与横轴夹角；v为机器人后轴中心点速度；φ为机器人前轮转向角；d为机器人前后轴中心点之间的距离。轴间距d为常值，可人工测得；转向角φ可根据舵机当前的偏转量求得；机器人的实际速度v可通过光电编码器测速模块测得，并输入单片机控制器，组成被控对象的速度闭环负反馈控制。

取状态变量 x1=xw，x2=yw，x3=θ~，其中θ~=θ-θ0，代表当前时刻车身方向夹角相对上一时刻夹角θ0（即当前时刻的基准参考量）的微小增量；取控制变量u1=v，u2=tanφ。 状态向量为 X（k）=（x1（k） x2（k） x3（k））T，观测向量为 Y（k）=（xw（k） yw（k））T，控制向量为U（k）=（u1（k） u2（k））T。

为了使模型更具普遍性，引入高斯白噪声。离散化后系统模型的线性方程组为

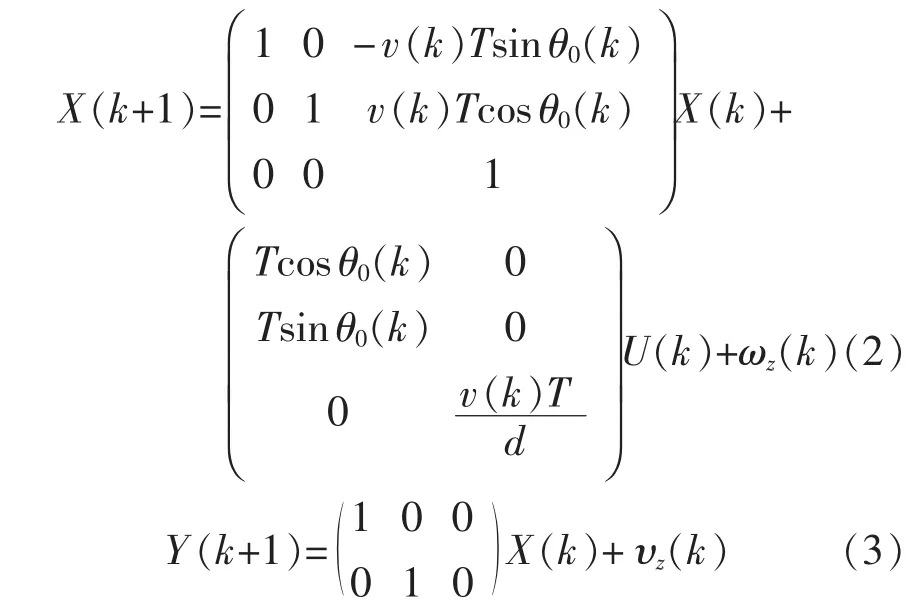
式中：T表示采样周期；ωz，υz分别为 3维的系统白噪声和2维的测量噪声，且0，其协方差分别为 Qz，Rz，且 Cov（wz，υz）＝0。

2.2 引入Kalman滤波器

为了得到更准确的系统状态信息，并获知机器人系统模型状态变量中不可直接测量的重要变量θ~，需要通过Kalman滤波器进行预估运算。经验证，该系统模型是能控能观的，因此可以引入全维Kalman观测器进行预估和校正，同时保证估计误差的方差和 E［X（k）-Xˆ（k|k-1））T（X（k）-Xˆ（k|k-1））］最小。其原理框图如图4所示。标准Kalman滤波器的基本工作步骤如下。

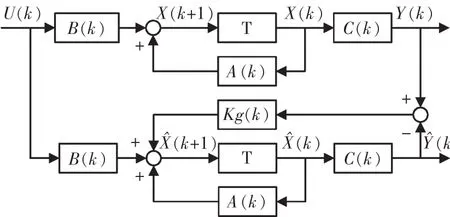
图4 Kalman滤波器原理框图Fig.4 Kalman filter diagram

第1步：预估：

（1）根据上一步的状态优化结果Xˆ（k-1|k-1）预估当前状态Xˆ（k|k-1）：

（2）计算当前预估值对应的系统协方差：

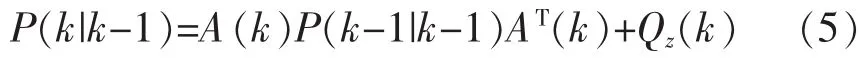
第2步：校正：

（1）优化 Kalman 增益：

（2）根据测量值及预估值，最优化当前状态：

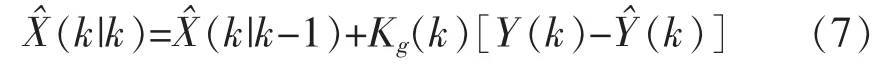
（3）最优化相应的系统协方差：

引入Kalman滤波器后，利用其预估作用，即使出现短期内目标观测值丢失的情况，仍然能够根据历史的相关值及状态信息推测出系统未来几步的预估信息，从而进行合理补偿，实现对移动机器人的全程准确控制。关于各矩阵的取法，Qz取一个非负定的定常矩阵；Rz取一个对称的正定定常矩阵。初始值X（0）和P（0）可根据系统实际运行情况进行赋值。

3 实验结果与分析

通过实验平台的实际运行效果分析本文所提模型及滤波算法的有效性。为了更直观地显示对多个目标的实际跟踪效果，实验选用2个四轮车式机器人作为目标在坐标从（0，0）到（400，600）的矩形平面有效监控范围内作直线运动，并检验最终的跟踪效果。

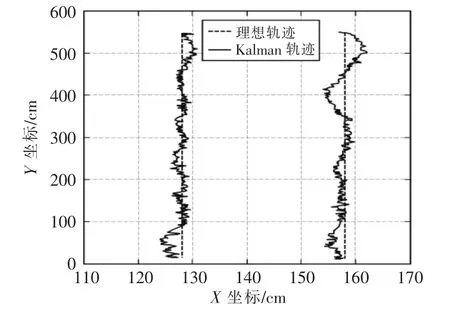
图5 机器人轨迹跟踪效果图Fig.5 Robot trajectory tracking renderings

图5是同时跟踪两台机器人移动轨迹的效果图。其中虚线代表理想轨迹，实线表示机器人的实际运动轨迹。由图可知，即使机器人的初始位置相比理想位置有所偏离，但是经过控制器的调整和Kalman滤波器的优化之后，跟踪轨迹将逐渐与理想轨迹趋于一致。在位置偏差的容许范围内，Kalman滤波算法的跟踪效果已达到要求。

图6是车式机器人的实时航向角及航向角增量的效果图。其中实线表示Kalman算法的优化值；虚线表示理想航向角，大约为-90°。从图可得，虽然滤波器给定的航向角状态的初值与小车实际的航向角有较大的偏差，但经过Kalman滤波器的不断预估、矫正和优化，估计值与实际值之间的稳态误差最终趋于较小的可容许范围，即对于该状态的预估能达到准确跟踪的要求。当滤波器的给定状态初始值越接近实际状态初始值时，Kalman对于状态的精确跟踪也将更加迅速。

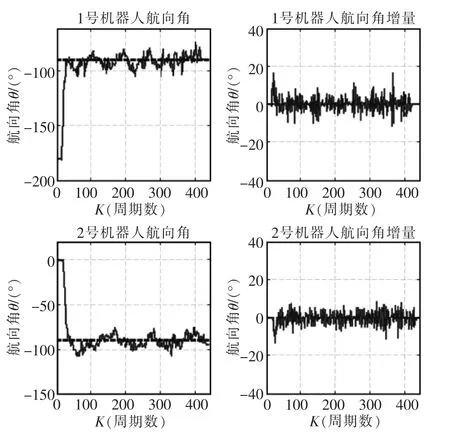
图6 机器人航向角跟踪效果Fig.6 Robot heading angle tracking renderings

4 结语

本文通过建立四轮车式移动机器人的模型，并对模型进行线性化和离散化等系列操作，使其适用于Kalman滤波算法的引入。通过成功将多Kalman滤波器应用到多个机器人控制系统，并利用实验平台验证Kalman滤波器对多机器人轨迹跟踪优化的效果，得出本文提出的算法及应用方法的合理性和有效性。实验结果表明Kalman滤波在车式移动机器人的轨迹跟踪中的应用能保证跟踪的精确度和实时性，并为进一步的机器人控制提供更多的状态信息，其中也包含一些无法被直接测量的状态。本文中对多目标的实时跟踪，为后续的模拟饱和攻击等方面的实现奠定了基础，对智能交通、高科技军事等领域的研究也提供了参考。

[1] Ristic B，Clark D E，Gordon N.Calibration of multi-target tracking algorithms using non-cooperative targets[J].IEEE Journal on Selected Topics in Signal Processing，2013，7 （3）：390-398.

[2] Anderson R J，Spong M W.Bilateral control of teleoperators with time delay[J].IEEE Transactions on Automation Control，1989，34（5）：494-501.

[3] Ai-Guo Wu，Guang-Ren Duan.Robust global stabilization for nonlinear systems with unmodeled dynamics by output feedback[C]//IEEE International Conference on Control and Automation，ICCA，2007：1129-1132.

[4] Shigeru H.Robust nonlinear model predictive control with variable blocklength[J].IEEE TRANSACTIONS ON AUTOMATIC CONTROL，2009，54（7）：1618-1622.

[5] Ling Zhao，Jing ZhiYe，Wen Feng Luo.A prototype target tracking network system for robot feedback control[J].Applied Mechanics and Materials，2012，157-158：1431-1435.

[6] Long Zhao，Hongyu Yan.An adaptive dynamic kalman filtering algorithm based on cumulative sums of residuals[C]//CSNC2013 Electronic Proceedings，2013，245：727-735.

[7] Hui-Ming Hung.Measurement of internally mixed aerosols acting as cloud condensation nuclei[C]//The 7th Cross-straits Air Adhesive Technology Workshop and the 2nd Air Pollution Technology Seminar，2010.

[8] Razak N A.A study of Kalman’s filter in embedded controller for real-time quadrocopter roll and pitch measurement[C]//Proceedings-2012 IEEE International Conference on Control System，Computing and Engineering，ICCSAE 2012：590-595.

[9] PopovA S.Synthesis of Kalman’s algorithm of functioning of an adaptive antenna array[C]//Proceedings of SPIE-The International Society for Optical Engineering，2008.

[10]QIU Xinyun，GAO Yuan.Adaptive PID controllerbased on single neuron[J].Applied Mechanics and Materials，2012，466-467：981-985. ■