水平井偏心环空顶替流体密度差优化

冯福平艾 池崔志华于法浩陈顶峰徐海粟

（1.东北石油大学提高油气采收率教育部重点实验室，黑龙江大庆 163318；2.吉林油田项目管理公司CO2驱建设项目部，吉林松原 138000）

水平井偏心环空顶替流体密度差优化

冯福平1艾 池1崔志华1于法浩1陈顶峰2徐海粟1

（1.东北石油大学提高油气采收率教育部重点实验室，黑龙江大庆 163318；2.吉林油田项目管理公司CO2驱建设项目部，吉林松原 138000）

顶替界面失稳指进造成的钻井液迟流是导致油气水窜槽的主要原因。水平井顶替界面受到套管偏心引起的宽窄间隙阻力效应和密度差引起的浮力效应共同影响，且两者对顶替界面的影响相反，因此有必要根据水平井套管偏心情况优化顶替流体密度差，从而提高顶替界面的稳定性。在总结三维数值模拟方法优缺点的基础上，采用该方法分析了水平井顶替界面长度随顶替时间的变化规律，以实现最小顶替界面长度为目标，得出了水平井套管偏心度与最优密度差之间的匹配关系。研究结果表明：水平井顶替界面长度随顶替时间增加增长幅度趋缓，但并不明显；在水平井套管偏心的情况下，密度差过大或过小都会降低顶替界面的稳定性，需要根据套管偏心度选取合理的密度差使得顶替界面长度最短。研究结果为水平井顶替参数和封固段长度设计提供了必要的理论依据。

顶替界面；数值模拟；水平井；偏心环空；密度差；水泥浆指进；钻进液迟流

固井顶替界面失稳指进造成顶替液掺混严重，边壁处迟流钻井液无法返出封固段，形成后期油气水窜槽的主要通道，因此形成稳定的顶替界面降低水泥浆指进程度是实现良好固井质量的前提。水平井顶替界面受到套管偏心引起的宽窄间隙阻力效应和密度差引起的浮力效应共同影响，并且两者对顶替界面的影响正好相反［1-4］，因此有必要考虑水平井套管偏心和密度差的综合作用进行顶替界面数值模拟分析，以实现最小顶替界面长度为目标，得到水平井套管偏心度与密度差之间的合理匹配关系，从而提高水平井偏心环空顶替效果，为水平井优势的发挥提供长期高效的环空封隔质量［5-6］。

1 顶替界面数值模拟的优缺点

水泥浆与钻井液的顶替界面反映了两相流体的掺混程度以及水泥浆的指进特征，是评价顶替效果的主要参数。由于实验条件的限制，无法进行各种不同顶替条件下的精确模拟，而数值模拟方法通过建立数值仿真模型，能够准确直观地显示不同顶替条件下的顶替界面形状，使得该方法成为进行固井顶替分析的有力工具。

采用数值模拟方法进行固井顶替分析的优点体现在：（1）摆脱实验研究受到实验条件及资金的限制，可以进行各种不同条件下顶替界面形状的精确模拟；（2）能够直观显示两种流体之间的相互掺混、脱离和指进等不稳定现象；（3）能够实时追踪不同间隙处顶替界面的运动位置。

但由于数值模拟软件的特点，采用数值模拟方法进行固井顶替分析也存在自身的不足。

（1）数值模拟软件在进行模拟时，假设无滑移边界条件，即除了边壁处，环空中任意一点的被顶替流体都会发生流动，只要顶替时间足够，图1中顶替界面L1、L2、L3左方的区域顶替效率全为100%，即该方法只能进行环空钻井液的迟流分析而无法描述钻井液的滞留现象。

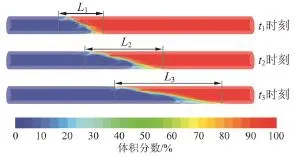
图1 套管居中情况下顶替界面随时间变化图

（2）数值模拟软件能够给出顶替界面的形状，顶替界面越稳定顶替效果就越好，但顶替界面形状与顶替效率之间并没有明确的对应关系。原因在于顶替效率体现的是顶替结束后环空的整体顶替效果，而数值模拟方法给出的是顶替界面上的顶替效率，而且顶替界面是时间和位置的函数，顶替界面上的局部顶替效果处于不断变化之中（图1中L1、L2、L3所示），其并不能代表环空整体顶替效率，只能通过顶替界面的稳定性来评价顶替效果的好坏。

2 顶替界面数值模拟的研究现状

顶替界面不仅反映了两相流体的掺混程度，同时也直观地描述了水泥浆指进造成的钻井液迟流现象，钻井液迟流是导致环空窜槽的主要原因。顶替界面越长，说明水泥浆指进现象越明显，顶替效果越差，迟流钻井液造成窜槽的可能性越大。因此可以通过数值模拟分析顶替界面长度的方法来评价顶替效果。国内外学者采用数值模拟的方法，针对直井偏心环空层流和紊流条件下注水泥顶替界面的稳定性及顶替效率进行了深入研究，得出了套管偏心度、顶替流速、顶替流体密度差及流变性能差异对顶替界面稳定性及顶替效率的影响［7-11］，但是对于水平井顶替界面稳定性的研究较少。直井无论是套管居中还是偏心条件下，顶替界面为水平剖面，密度差产生的浮力作用在水平剖面上各点一致，顶替流体密度差越大，顶替界面越稳定，这一结论得到了国内外专家的广泛认可；但水平井中顶替界面为垂直剖面，密度差产生的浮力作用还与该点到上井壁的垂直距离有关，密度差产生的浮力作用在顶替界面上各点都不相同，因此水平井顶替界面形状及影响因素与直井有较大的不同。李明忠［2］对大斜度井偏心环空中套管偏心及水泥浆与钻井液的密度差对顶替效率的影响进行了分析，张松杰［3-4］分析了水平井偏心环空冲洗隔离液、水泥浆与钻井液的密度差对顶替界面的影响，通过研究得出了顶替界面长度的变化规律及套管偏心与密度差之间的相互作用。

但目前研究主要存在以下几个问题。

（1）采用数值模拟方法进行顶替效果分析大多是以顶替效率来进行评价的，而数值模拟方法并不能通过顶替界面形状得出明确的顶替效率，因此分析的角度是不恰当的。

（2）顶替结束时迟流钻井液没有返出封固段的话必定会形成环空窜槽的通道，因此准确进行迟流钻井液运动位置分析是进行替浆设计的关键。顶替界面的位置及形状随着顶替时间不断变化，文献［3-4］中提到了顶替界面长度随时间的变化规律，但其关于顶替界面长度与顶替时间之间的关系有待商榷。

（3）水平井中顶替界面及水泥浆指进现象不仅与顶替流体的流变性能有关，同时还与套管偏心度以及顶替流体的密度差有关，顶替界面受到套管偏心引起的宽窄间隙阻力效应和密度差引起的浮力效应共同影响，且两者引起的作用相反，因此对于水平井偏心环空来说存在合理的密度差，从而使得顶替界面最为稳定，水泥浆指进程度最低，但目前研究并未给出水平井套管偏心度与最优密度差之间的匹配关系。

3 数值仿真模型及求解

综合考虑了水平井套管偏心引起的宽窄间隙阻力效应和密度差引起的浮力效应，采用三维数值模拟的方法，首先分析了顶替界面长度随顶替时间的变化规律，在此基础上对不同偏心度、不同密度差条件下的顶替界面长度进行了模拟分析，以降低环空顶替界面长度为目标，得出了水平井套管偏心度与最优密度差之间的合理匹配关系，从而为水平井顶替参数的优化设计提供必要的理论依据。

3.1 流体本构模型及基本性能参数

赫—巴流变模型同时包含了宾汉流体和幂律流体两种流变模式的特点，可以较为充分地反映顶替流体的流变特性，因此选择顶替流体为赫—巴流变模型。

赫—巴流体本构方程为

式中，τ0为屈服应力，Pa；K为赫—巴流体稠度系数，Pa·sn；n为赫—巴流体的流性指数；T为偏应力张量；A1为一阶里夫林—埃里克森张量；∏为A1的第二不变量；tr表示对矩阵取迹，即对角线元素之和。

模拟过程中选取的流体基本性能参数见表1。

表1 模拟流体基本性能参数

3.2 数值模拟物理模型

模拟井筒直径230 mm，套管外径139.7 mm；进行顶替界面长度与时间的关系分析时选取水平段长度为100 m，其余取为20 m；只考虑套管向下的偏心作用，偏心度分别为0、0.1、0.2、0.3、0.4、0.5；模拟过程中把连续解析的流场空间离散成有限个离散节点，在流场每个节点上计算随时间变化的密度、速度、压力等物理量，分别建立两个假想面，捕捉水泥浆与钻井液顶替界面的前缘与后缘位置。

3.3 控制方程及求解

水平井固井顶替属于液、液两种流体在长距离环空间隙中的流动过程，满足流体力学基本方程，包括连续性方程、动量方程及层流方程构成的一组微分方程组。

控制方程为三维非定常N-S方程

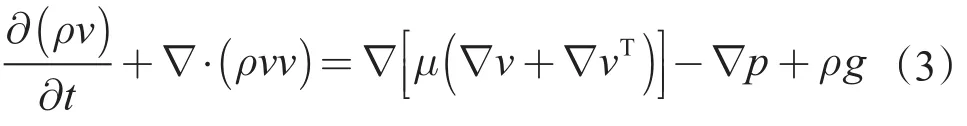
式中，ρ为密度，kg/m3；v为速度，m/s；p为压力，Pa；μ为动力黏度，Pa·s；g为重力加速度，m/s²。

采用流体体积法进行界面的跟踪与重构，该方法所用到的容积比率方程为

式中，a代表某相液体在控制体内的体积分数，下标1和2分别代表控制体内的不同相。

容积比率方程ai=0，代表流体中不含有j相；ai=1，代表流体中全部为j相；0＜ai＜1，流体中既含有i相，又含有j相。

对数值方程进行离散时，在空间上采用结构化的六面体网格和单精度有限体积方法。时间上采用隐格式，对流项采用一阶迎风有限元离散格式，利用改良后的压力速度校正方法求解压力速度场的耦合。

入口为速度边界条件，顶替速度为1.0 m/s，层流顶替，出口为出流边界，壁面速度按无滑移边界条件处理，时间步长为0.01 s。

3 顶替界面长度随时间变化规律

顶替界面越长，水泥浆指进现象越严重，顶替效果越差。顶替结束时迟流钻井液没有返出封固段的话必定会形成环空窜槽的通道，因此准确进行迟流钻井液运动位置分析是进行替浆设计的关键。为了分析顶替界面随时间的变化规律，水平段长度取为100 m，只对套管居中、密度差0.6 g/cm3条件下的顶替界面长度进行了模拟，由模拟结果可知在顶替时间达到89 s时顶替界面前缘已经到达模型出口端，顶替界面长度随时间的变化如图2所示。

从图2可以看出，在密度差的作用下，水泥浆在低边发生明显的指进现象，顶替界面长度随顶替时间增加增长幅度趋缓，但并不明显。这一结果与文献［4］有一定的差别，笔者分析可能原因在于文献［4］中模型长度为12 m，流速为1 m/s，顶替时间还未达到12 s时，顶替界面前缘已经超出模型出口端，无法追踪顶替界面前缘位置，默认顶替界面前缘还处于出口端附近，导致顶替界面长度增加幅度趋缓明显。

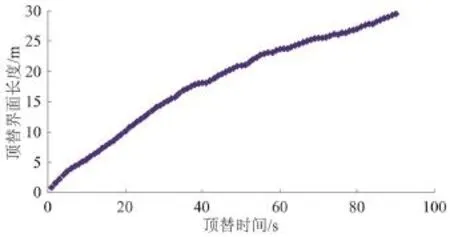
图2 顶替界面长度随时间变化

根据数值模拟结果，选择合理的趋势线类型，可以得出顶替界面长度与顶替时间的拟合关系式为

通过该公式即可得出不同顶替时间的顶替界面长度，如表2所示。

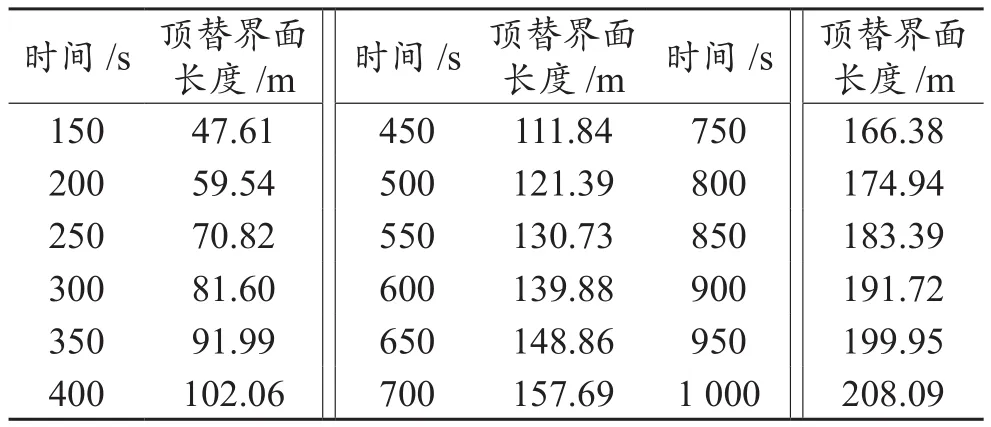
表2 顶替界面长度与时间关系

4 水平井偏心环空顶替流体密度差优化

水平井套管向下偏心使得水泥浆沿宽边即上井壁方向发生指进，而水泥浆与钻井液密度差产生的浮力效应越靠近下井壁方向越大，使得下井壁方向的水泥浆指进趋势明显，套管偏心和密度差对顶替界面的影响正好相反，因此需要对两种因素共同作用下的顶替界面形状进行综合分析。图3为不同套管偏心度及密度差条件下顶替界面长度模拟结果。从模拟结果可以看出如下规律。

（1）水平井套管居中时，不存在宽窄间隙引起的阻力效应，在固井顶替时只存在密度差引起的浮力效应，密度差越大，浮力效应所引起的指进现象越明显，顶替界面长度就越大，顶替效果逐渐变差。因此，水平井套管居中时，水泥浆与钻井液的密度差越小顶替效果越好。

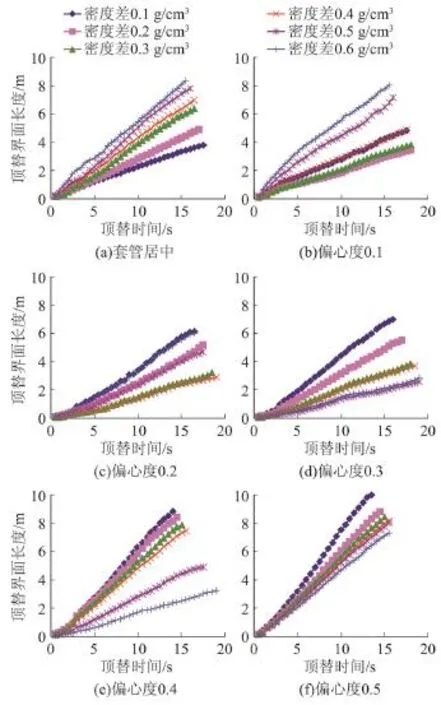
图3 不同套管偏心度及密度差条件下顶替界面长度随时间变化

（2）对于同一偏心度来说，密度差较小时，密度差引起的浮力效应不足以克服套管偏心引起的宽窄间隙阻力效应，使得顶替界面沿上井壁产生指进；密度差较大时，密度差引起的浮力效应大于套管偏心引起的宽窄边阻力效应，使得顶替界面沿下井壁产生指进。密度差过大或过小都会造成顶替界面长度增加，因此为了使得顶替界面平齐推进，降低指进程度，需要根据套管偏心度选取合理的密度差使得顶替界面长度最短。

（3）顶替界面长度越短，顶替前缘位置到达出口端的时间越长，水泥浆指进程度越弱，顶替界面越稳定。

（4）套管偏心0.1时，密度差为0.2 g/cm3时顶替界面长度最短，顶替效果最好；套管偏心0.2时，密度差为0.4 g/cm3时顶替界面长度最短，顶替效果最好；套管偏心0.3时，密度差为0.5 g/cm3时顶替界面长度最短，顶替效果最好；套管偏心度大于等于0.4时，密度差越大顶替界面长度越短，说明模拟所采用的最大密度差0.6 g/cm3所引起的浮力效应也不能克服宽窄间隙阻力效应引起的指进现象，水泥浆均沿上井壁发生指进。

（5）上述不同偏心度下对应的最优密度差，是在所模拟的0.1、0.2、0.3、0.4、0.5、0.6 g/cm3这6个密度差内的最优值，实际每个偏心度对应的理论最优密度差会有一定的差别，根据不同密度差条件下顶替界面长度与套管偏心度之间的关系（图4），可以拟合出在模拟参数条件下套管偏心度与最优密度差之间的匹配关系为

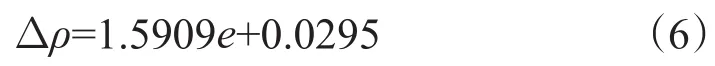
式中，Δρ为水泥浆与钻井液的密度差，g/cm3；e为套管偏心度。

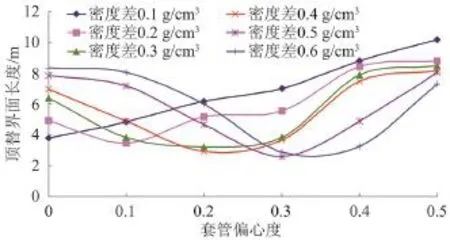
图4 不同密度差条件下顶替界面长度与套管偏心度之间的关系图

水平井固井顶替时，可以根据现场扶正器下入数量及类型计算套管偏心度，通过模拟计算得到的最优匹配密度差来设计水泥浆密度，从而降低顶替界面长度和水泥浆指进程度，提高固井顶替效果。

5 结论

（1）数值模拟方法得到的顶替界面形状能够直观地显示两相流体的掺混程度以及水泥浆的指进特征，为固井顶替理论分析提供了有力的手段，但其不能反映顶替效率的具体数值，同时也不能描述钻井液的滞留现象。

（2）顶替流体密度差越大，直井顶替界面越稳定；而水平井套管偏心引起的宽窄间隙阻力效应和密度差引起的浮力效应对顶替界面的影响相反，因此水平井套管偏心条件下并不是密度差越大顶替界面越稳定，而是存在合理的密度差使得顶替界面最为平稳。

（3）水平井顶替界面长度随顶替时间增加增长幅度趋缓，但并不明显。迟流钻井液造成封固段环空窜槽，因此必须根据顶替界面的运动规律合理设计替浆量和封固段长度。

（4）在水平井套管偏心的情况下，密度差较小时顶替界面沿上井壁产生指进，密度差较大时顶替界面沿下井壁产生指进。密度差过大或过小都会降低顶替界面的稳定性，因此为了使得顶替界面平齐推进，降低水泥浆指进程度，需要根据套管偏心度选取合理的顶替流体密度差使得顶替界面长度最短。

［1］冯福平，艾池，彭万勇，等.套管偏心对水平井顶替效果的影响［J］.石油钻采工艺，2011，33（3）：12-16.

［2］李明忠，王成文，王长权，等.大斜度井偏心环空注水泥顶替数值模拟研究［J］.石油钻探技术，2012，40（5）：40-44.

［3］张松杰，薛亮，汪志明，等.密度差对水平井固井顶替影响规律数值模拟研究［J］.钻采工艺，2012，35（6）：15-17.

［4］张松杰，薛亮，汪志明，等.正密度差对水平井偏心环空顶替影响规律研究［J］.科学技术与工程，2013，13（4）：1011-1015.

［5］刘成贵.非常规油气水平井固井关键技术研究与应用［J］.石油钻采工艺，2013，35（2）：48-51.

［6］刘伟，陶谦，丁士东.页岩气水平井固井技术难点分析与对策［J］.石油钻采工艺，2012，34（3）：40-43.

［7］DUTRA E S S,NACCACHE M F,MENDES P R S.Liquid displacement during oil well cementing operations［J］.Annual transactions of the Nordic Rheology Society,2004,12（1）:93-100.

［8］高永海，孙宝江，刘东清，等.环空水泥浆顶替界面稳定性数值模拟研究［J］.石油学报，2005，26（5）：119-122.

［9］杨建波，邓建民，冯予淇，等.低速注水泥时密度差对顶替效率影响规律的数值模拟研究［J］.石油钻探技术，2008，36（5）：62-65.

［10］PKS S,YERUBANDI K B.Slim-well completions:a 3D numerical approach for displacement to design effective cementing fluids［R］.SPE 132480,2010.

［11］ARANHA P E，MIRANDA C R,MAGALHAES J V M,et al.Dynamic aspects governing cement plug placement in deepwater wells［R］.SPE 140144,2011.

（修改稿收到日期 2013-12-28）

〔编辑 朱 伟〕

Density difference optimization of displacing fluids in eccentric annulus of horizontal wells

FENG Fuping1,AI Chi1,CUI Zhihua1,YU Fahao1,CHEN Dingfeng2,XU Haisu1
（1.Key Laboratory of Education Ministry for Enhanced Oil Recovery,Northeast Petroleum University,Daqing163318,China;2.Project Construction Department of Carbon Dioxide Miscible Flooding,Jilin Oilfield Project Management Company,Songyuan138000,China）

Slow-flow drilling fluid caused by fingering instability of displacement interface is the main factor to result in oil/gas/ water channeling.The displacement interface in horizontal wells is affected by resistance effect in narrow and wide clearances caused by casing eccentricity and buoyancy effect caused by density difference.Besides,impacts of the two factors on displacement interface are opposite.Therefore,displacement interface stability can be enhanced by optimizing the density difference of displacing fluids based on casing eccentricity in horizontal wells.The change law of the displacement interface length with time is analyzed based on the advantages and disadvantage of the method of three-dimensional numerical simulation to realize the target of minimum displacement interface length and have the matching relationship between the optimal density difference and casing eccentricity.The conclusions are as follows:the growth rate of displacement interface length slows down with time increasing,but it is not obvious;the too large or small density difference will reduce the displacement interface stability in the eccentric annulus of horizontal wells.In order to achieve the shortest displacement interface length in cementing,reasonable density difference shall be chosen on the basis of casing eccentricity.The study results provides theoretical basis for the design of displacement parameters and cementing length in horizontal wells.

displacement interface;numerical simulation;horizontal wells;eccentric annulus;density difference;slurry fingering;slow-flow drilling fluid

冯福平，艾池，崔志华，等.水平井偏心环空顶替流体密度差优化［J］.石油钻采工艺，2014，36（1）：61-65.

TE256

：A

1000-7393（2014）01-0061-05

10.13639/j.odpt.2014.01.016

黑龙江省青年科学基金“深井硬地层研磨机理及对可钻性评价的影响研究”（编号：QC2012C021）。

冯福平，1982年生。2005年毕业于大庆石油学院石油工程专业，主要从事油气井工程力学方面的教学和科研工作，博士研究生，讲师。E-mail：fengfuping2005@163.com。