连续变量基于灵敏度和特异度的一次多项式函数选择最佳诊断界点的方法*

南方医科大学公共卫生与热带医学学院生物统计学系（510515） 朱玲湘 陈平雁

连续变量基于灵敏度和特异度的一次多项式函数选择最佳诊断界点的方法*

南方医科大学公共卫生与热带医学学院生物统计学系（510515） 朱玲湘 陈平雁△

在诊断试验评价中，最佳诊断界点（cut-off point）的选择一直是个尚未完全解决的热点问题。该问题涉及两个方面，一是“最佳”的标准，二是寻找最佳诊断界点的方法。目前关于最佳诊断界点的确定多以评价指标值最大化为标准。事实上，依此标准确定的最佳点有时只是数理上的最大值，但在实际临床上可能并无实用价值。在如何寻找最佳诊断界点方面，Metz提出借助ROC曲线采用图像的方法选择最佳诊断界点［1］，随后Greiner等对比数积、似然比、Kappa系数等在图像上做了更深入的研究［2-3］，但都只是展示出几何表现的不同，并没有从实质上给出具有实际操作性的一般计算方法。事实上，ROC曲线是所有可能诊断界点的直观几何表现，而评价指标才真正地决定选择诊断界点的策略。直至近年Perkins等在两个连续变量服从正态分布假设下，研究了关于Youden指数最大值点一般计算方法［2-10］。关于其它的评价指标目前仍然缺少确定最佳诊断界点的一般计算方法。一个完整、有效的诊断试验评价不仅包含评价指标的计算，还应给出在该指标下相应的最佳诊断界点确定标准及计算方法，以适应不断发展的诊断医学的研究。

不同的评价指标拥有各自对应的最佳诊断界点。要建立确定最佳诊断界点的一般方法，首先要确定评价指标的形式。为评价诊断试验的效果，最常用的诊断试验准确度指标是灵敏度（sen）和特异度（spe）［11］。由于这两个指标呈负相关关系，分别使用这两个指标进行不同诊断方法之间的比较受到一定限制，因此产生了许多组合灵敏度和特异度而形成的综合评价指标，如Youden指数和加权Youden指数，诊断准确率，诊断比数积，阳性似然比和阴性似然比，kappa系数、预测值，信息量等［12-20］。对于这些评价指标，我们均可以将其视为关于灵敏度和特异度的函数。我们可以根据相应的函数形式把其分为两类，第一类是关于sen和spe的多项式函数，包括Youden指数、加权Youden指数、诊断准确率；第二类是除第一类外的所有评价函数，其中大部分是关于sen和spe有理分式函数，如诊断比数积，似然比等。如果我们将第一类归结为关于sen和spe的一次多项式函数，其中每个指标都是该一次多项式函数的一个特例，那么，我们就可以从更一般的角度探讨综合评价指标的建立以及相对应的寻找最佳诊断界点的方法，这正是本研究的目的所在。至于第二类函数，尚不是本研究所考虑的内容。

诊断试验一次多项式综合评价指标的定义

用Y和X分别代表对照组与病例组的连续型变量，非负可积函数fY（t）、fX（t）分别为相应的概率密度函数。假设Y和X均服从正态分布，即Y～N（μY，在此不妨假设μY＜μX（事实上，当μX＜μY时，只需调转Y和X的位置即可）。此时，对任意的诊断界点c，对应的灵敏度和特异度有如下表达式

灵敏度和特异度不再是关于c的初等函数，而只能用变限积分来表示。一般来说，fY（t）和fX（t）下的面积中有相当一部分重叠区域（如图1），这正是导致最佳诊断界点难以确定的原因。

一般的基于灵敏度和特异度的一次多项式评价函数则可表述为式（2），

其中λX、λY、α0为定常数，且λX＞0、λY＞0。另一个角度，可以将λX、λY看成灵敏度和特异度的权重，当它们取不同的值时，可以得到不同的诊断试验评价指标。可见，任何形式的一次评价函数都可以化为式（2）的形式，可将其作为基于灵敏度和特异度的一次多项式评价函数的标准形式。采用以上定义，在诊断试验中希望ψ最大化。

图1 两个正态分布总体的密度函数

特别地，当λX＝r、λY＝1-r、α0＝0（r为病例组占比）时，式（2）即化为诊断准确率［21-22］；

当λX＝1、λY＝1、α0＝-1时，式（2）退化为Youden指数［16］；

当λX、λY、α0为不同的赋值组合时，式（2）退化为加权Youden指数［23-26］。

把式（1）代入上式，可得到的是进一步化为关于诊断界点c的函数

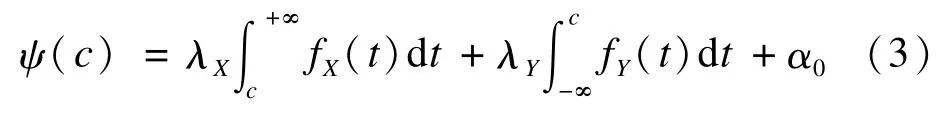
显然ψ（c）为实数域上连续可导函数，其最大值点一定在驻点取得。

基于一次多项式函数选择最佳诊断界点的方法

在确定最佳诊断界点之前，必须先对其判别标准重新定义。以往的研究认为最佳诊断界点是使评价指标ψ（c）取得最大值的点，这个定义是不严谨的。比如，在使用诊断准确率作为试验的评价指标时，恰逢发病率极低的疾病，我们将诊断界点确定在一个较高的水平上如图2的点c，甚至是更大的临界值，那么大部分受试者均诊断为阴性，从而得到较高的诊断准确率。但按照这样的诊断标准会导致较大的漏诊率。这样的诊断界点尽管达到了诊断准确率最大值，但在临床上却失去了实用价值。

图2 两个正态分布总体假设下无实际意义的最佳诊断界点

由此，两个正态分布总体假设下，最佳诊断界点c*需同时满足两个条件：

i）使评价指标ψ（c）取得最大值，即ψ（c*）＝maxψ（c）；

ii）在临床诊断中具有实际意义，即c*∈（μY，μX）。那么重新定义后的最佳诊断界点可以表示为｛c｜maxψ（c）∩（μY，μX）｝。换言之，若｛c｜maxψ（c）｝与（μY，μX）没有交集，那么就要重新考虑测量指标及评价指标是否合适。尤其要注意的是，最佳诊断界点与在区间上（μY，μX）函数ψ（c）的最大值点是不同的。

按照上述标准，进一步给出最佳诊断界点的确定方法。

首先，令ψ（c）导函数为0，得

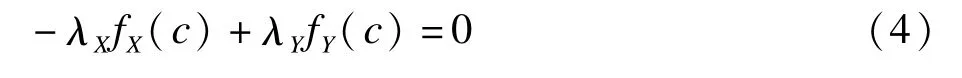
方程作形式改变后得

可以看到ψ（c）的最大值点一定是对照组与病例组密度函数之比恰等于灵敏度与特异度的权重之比。

在两种不同情况下解方程（4）。

该点在图像上即两概率密度函数曲线位于两均值间的中点。

因此，若式（5）同时满足c∈（μY，μX），那么有

否则，在该诊断试验中，最佳诊断界点不存在。此时，需要斟酌测量指标及评价指标的选取是否合适。在实际处理中，若将对照组数据进行标准化，而病例组数据做同样的线性变换，则可直接得到（9）所示结果。可以清楚看到界点的绝对位置由μ、σ、λ三者共同决定。相比之下，对式（9）进行讨论确定最佳诊断界点要简单的多，我们称该式为标准化数据后的诊断界点。同时Δ≥0的条件可解释为：当σ2＞1，且λ2≤σ2·exp时方程有解。但此时仅是方程的解，要确定为最佳诊断界点，还必须满足在区间（0，μ）内，即

特别当λ＝1时，最佳诊断界点在图像上为两密度函数交点。即

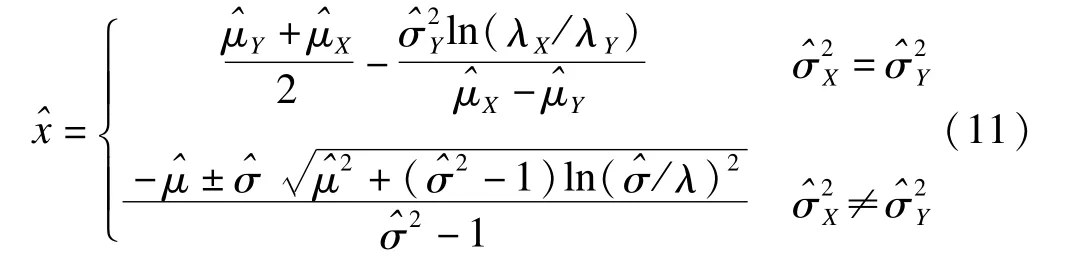
实 例

为更清楚阐明以上方法，以冠心病研究中关于氧化低密度脂蛋白（ox-LDL）水平的诊断试验为例寻找最佳诊断界点。目前关于ox-LDL的研究中，多认为冠心病患者循环中ox-LDL水平明显增高。因此可将其作为诊断冠心病风险的一项生化指标来区别患病与否［27-32］。在中山大学第一附属医院心血管科的一项对照诊断研究中［33］，先后测得对照组ox-LDL的均数和标准差分别为0.490和0.267；病例组分别为2.028和0.896。在此，用样本估计的总体参数分别为

首先计算Youden指数及相应最佳诊断界点，可以得c1＝1.0053，c2＝-0.3251。显然，取c*＝1.0053，并计算相应的spe（c*）＝0.9732，sen（c*）＝0.8732，J（c*）＝0.8646。还可以采用前面提到的加权Youden指数进行评价［23］，假设λX、λY有不同赋值组合的情况下，同时令α0＝0，依次计算Δ、c1、c2，并给出最佳诊断界点c*，计算相应spe（c*）和sen（c*），所得结果均列在表1。

表1 不同λX，λY赋值时的最佳诊断界点

由表中可看到，当λX＝0.01，λY＝0.99时，得到c1＝1.4179、c2＝-0.7377，因为0.490＜c1＜2.028，故c*＝1.4179。随后计算相对应的spe（c*）＝0.9997，sen（c*）＝0.7520，ψ（c*）＝0.9973。当λX＝0.50，λY＝0.50时，得到c1＝1.0053、c2＝-0.3251，因为0.490＜c1＜2.028，故c*＝1.0053，随后计算相对应的spe（c*）＝0.9732，sen（c*）＝0.8732，ψ（c*）＝0.9232。当λX＝0.94，λY＝0.06时，得到c1＝0.4491、c2＝0.2311，因为c1，c2＜0.490，故不存在c*。而当λX＝0.95，λY＝0.05时，因为Δ＝-0.1712，故不存在c*。若出现后面这两种情况，那么需要重新考虑评价指标ψ（c）中的赋值λX、λY是否合适，如果指标合适，则需进一步考虑该诊断试验中测量指标的选取是否合适。

换个角度来看，上面的计算也可以看成计算诊断准确率的情况，不同的λX表示不同的发病率，会看到当发病率不同时得到的诊断界点也是不同的，甚至有不存在最佳诊断界点的情形。当然对于一个诊断试验来说，一旦试验对象确定，那么发病率就是固定的，而不能像加权Youden指数那样来赋予不同的权重组合，在这里只是通过该例子来说明发病率对最佳诊断界点位置的影响。

讨 论

在本文中可以看到，对于公式（3）所示的评价指标，不同的λX、λY是通过比值λ改变最佳诊断界点的位置，而α0的变化不会改变诊断界点的位置。对于同一诊断试验，只要比值λ相同，那么得到的是相同的诊断界点。就像在表1中，当λX＝0.50，λY＝0.50时，得到的c*与λX＝1，λY＝1时即在Youden指数中计算的c*是相同的，因此得到的spe（c*）和sen（c*）也相同。但J（c*）＜ψ（c*），这是由于在J（c*）、ψ（c*）中，α0分别为-1和0造成的。Δ随着λ的增大而减小，因此会出现λ过大或过小的极端情形，导致评价指标ψ（c）没有驻点，从而找不到最佳诊断界点c*。表1中当λX＝0.95，λY＝0.05时就属此情形。此时，需要再次考虑两个问题：（1）该评价指标中的λX、λY的选取是否合适；（2）在给定λX、λY的评价方案下，该诊断试验的方法及观测变量的选取是否有价值。

本文根据评价指标的函数形式进行分类，建立关于灵敏度和特异度的一次多项式评价函数的标准形式，该表达式通过待定系数来表征不同的诊断试验评价指标。在两个正态分布总体的假设下，结合评价指标最大化提出了最佳诊断界点的新定义。基于前面的假设，分别从病例与对照组方差相等和方差不等的情形分析最佳诊断界点是否存在。当最佳诊断界点存在时，给出相应的计算公式，并对影响该界点位置的因素以及影响方式进行详细讨论。结果表明观测变量的分布参数以及评价指标中灵敏度与特异度的权重共同决定了最佳诊断界点的位置。文中最后对未得到最佳诊断界点的情况给出了直观和合理的解释。

1.Metz CE.Basic principles of ROC analysis.Semin Nucl Med，1978，8（4）：283-298.

2.Greiner M，Pfeiffer D，Sm ith RD.Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests.Prev Vet Med，2000，45（1-2）：23-41.

3.Greiner M，Gardner IA.Epidem iologic issues in the validation of veterinary diagnostic tests.Prev VetMed，2000，45（1-2）：3-22.

4.Fluss R，Faraggi D，Reiser B.Estimation of the Youden Index and its associated cutoff point.Biom J，2005，47（4）：458-472.

5.Perkins NJ，Schisterman EF，Vexler A.Generalized ROC curve inference for a biomarker subject to a lim itof detection andmeasurementerror.Stat Med，2009，28（13）：1841-1860.

6.Schisterman EF，Perkins NJ，Liu A，et al.Optimal cut-point and its corresponding Youden Index to discrim inate individuals using pooled blood samples.Epidem iology，2005，16（1）：73-81.

7.Perkins NJ，Schisterman EF，Vexler A.Receiver operating characteristic curve inference from a samplew ith a lim it of detection.Am JEpidem iol，2007，165（3）：325-333.

8.Ruopp MD，Perkins NJ，Whitcomb BW，et al.Youden Index and optimal cut-point estimated from observations affected by a lower lim it of detection.Biom J，2008，50（3）：419-430.

9.Perkins NJ，Schisterman EF.The Youden Index and the optimal cutpoint corrected formeasurement error.Biom J，2005，47（4）：428-441.

10.Perkins NJ，Schisterman EF.The inconsistency of“optimal”cutpoints obtained using two criteria based on the receiver operating characteristic curve.Am JEpidemiol，2006，163（7）：670-675.

11.Yerushalmy J.Statistical problems in assessing methods of medical diagnosis，w ith special reference to X-ray techniques.Public Health Rep，1947，62（40）：1432-1449.

12.陈平雁，郭祖超.比较两种诊断试验的统计方法.

13.陈平雁，王斌会.几种诊断试验统计方法的比较.

14.陈平雁.诊断试验的评价指标及其应用.

15.陈平雁，胡琳.评价诊断试验的信息量方法.

16.Youden WJ.Index for rating diagnostic tests.Cancer，1950，3（1）：32-35.

17.Vecchio TJ.Predictive value of a single diagnostic test in unselected populations.N Engl JMed，1966，274（21）：1171-1173.

18.Glas AS，Lijmer JG，Prins MH，et al.The diagnostic odds ratio：a single indicator of test performance.JClin Epidem iol，2003，56（11）：1129-1135.

19.Cohen JA coefficient of agreement for nom inal scales.Educational and psychologicalmeasurement，1960，20（1）：37-46.

20.Metz CE，Goodenough DJ，Rossmann K.Evaluation of receiver operating characteristic curve data in terms of information theory，w ith applications in radiography.Radiology，1973，109（2）：297-303.

21.Guinan P，Bush I，Ray V，et al.The accuracy of the rectal examination in the diagnosis of prostate carcinoma.New England Journal of Medicine，1980，303（9）：499-503.

22.Galen RS，Gambino SR.Beyond normality：the predictive value and efficiency ofmedical diagnoses.W iley New York，1975.

23.Rucker G，Schumacher M.Summary ROC curve based on a weighted Youden index for selecting an optimal cutpoint in meta-analysis of diagnostic accuracy.Stat Med，2010，29（30）：3069-3078.

24.Li D，Shen F，Yin Y，et al.Weighted Youden index and its two-independent-sample comparison based on weighted sensitivity and specificity.Chinese Medical Journal，2013，126（6）：1150-1154.

25.Zhou X，ObuchowskiNA，M cclish DK.Statisticalmethods in diagnostic medicine.Wiley，2011.

26.李丹玲，陈平雁.基于灵敏度和特异度任意赋权的广义标准化诊断符合率.2011.

27.Kampus P，Kals J，Ristimae T，etal.Augmentation index and carotid intima-media thickness are differently related to age，C-reactive protein and oxidized low-density lipoprotein.JHypertens，2007，25（4）：819-825.

28.Shimada K，Mokuno H，Matsunaga E，et al.Circulating oxidized lowdensity lipoprotein is an independent predictor for cardiac event in patients w ith coronary artery disease.Atherosclerosis，2004，174（2）：343-347.

29.Holvoet P，Harris TB，Tracy RP，et al.Association of high coronary heart disease risk statusw ith circulating oxidized LDL in the well-functioning elderly：findings from the Health，Aging，and Body Composition study.Arterioscler Thromb Vasc Biol，2003，23（8）：1444-1448.

30.Suzuki T，Kohno H，Hasegawa A，et al.Diagnostic implications of circulating oxidized low density lipoprotein levels as a biochem ical risk marker of coronary artery disease.Clin Biochem，2002，35（5）：347-353.

31.Isomaa B，Almgren P，Tuom i T，et al.Cardiovascular morbidity and mortality associated w ith themetabolic syndrome.Diabetes Care，2001，24（4）：683-689.

32.Holvoet P，Vanhaecke J，Janssens S，etal.Oxidized LDL andmalondialdehyde-modified LDL in patients w ith acute coronary syndromes and stable coronary artery disease.Circulation，1998，98（15）：1487-1494.

33.Huang H，MaiW，Liu D，et al.The oxidation ratio of LDL：a predictor for coronary artery disease.Dis Markers，2008，24（6）：341-349.

（责任编辑：郭海强）

*国家自然科学基金资助（30972554；81273191）

△通信作者：陈平雁