线性回归中自变量重要性估计的平均秩序方差分解法*

贾孝霞伍立志沈其君，2△

线性回归中自变量重要性估计的平均秩序方差分解法*

贾孝霞1伍立志1沈其君1，2△

19世纪以来，在自变量间存在多重共线性时估计自变量相对重要性的方法研究取得了较大地突破和快速地发展［1-2］。Lindeman于1980年［3］，Cox于1985年［4］和Kruskal于1987年［5-6］分别提出了基于平均秩序产生不同的方差分解法估计每个自变量对因变量的重要性。在1992和2000年，Soofi［7-8］等人提出了一个正式的判定方法和在一个统一准则的基础上提出了以最大化熵为基础的平均所有次序的一般化的方法。近几十年来，许多研究者从不同的角度重新改造和发展了这个理论，同时对每种方法以不同的名字命名。而实际上，这些方法的提出都是基于Shapely在1953年提出的对策理论的Shapley值的求解方法。

平均秩序的方差分解法

1.平均半偏相关系数平方法

平均半偏相关系数平方法也称LMG法［3］是由Lindeman、Merenda和Gold于1980年提出，于1987年由Kruskal［5-6］推广而被广泛关注［9］。该方法是分别取三位学者名字的首字母而命名。该方法对于p个自变量的所有P！可能的排序，估计Xk的贡献公式为：

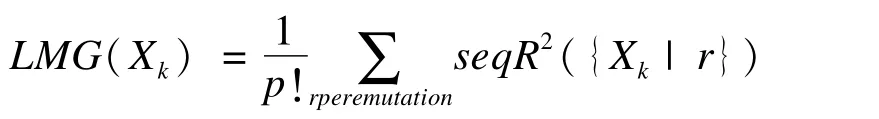
其中，序列记为r，r＝1，2…，p！；seqR2（｛Xk｜r｝）为在第r个排序中自变量Xk所在模型的连续平方和。

2.比例边界方差分解法

比例边界方差分解法也称Proportional Marginal Variance Decomposition（PMVD）［10-12］，是由Feldman于2005年在LMG方法上做了一个加权提出的一种方法。计算公式为：

3.分层划分法

分层划分法也称Hierarchical Partitioning［14］，是由Chevan和Sutherland于1991年提出，这种方法指出因变量y和xi间的相关系数的平方r2划分为一个独立成分Ii和一个联合成分Ji。其关系表达式为：

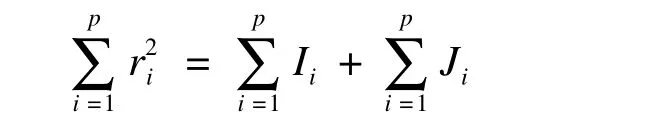
文献指出，如果用R2测量模型拟合优度，那么为正，表明相关自变量含有关于y的冗余信息。有时为负，说明相关自变量含有关于y的冗余信息有时是错误的［15］。

4.优势分析法

优势分析也称Dominance Analysis（DA）［16-20］，是由Budescu和Azen于1993年提出，于2003年进一步完善的自变量重要性的估计方法。优势分析中自变量xi的重要性计算公式为：

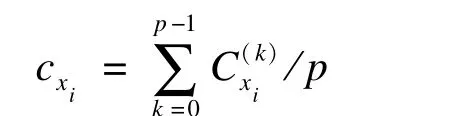
5.对策理论法

对策理论法也称Shapley Value（SV）［21-26］，是由Lipovetsky和Conklin于2001年提出［21］，Conklin［22］于2004年进一步完善的自变量重要性估计方法。这种方法对自变量xi的重要性估计公式如下：

6.信息测量法

信息测量法也称Information Measures［27-28］，是由Theil于1987年，Theil和Chung于1988年利用平均次序的思想但是使用不同的统计信息理论测量方法提出的一种方法。R2的信息测量定义为p个自变量半偏相关系数平方的信息和，其关系式表达为：

其中，I（x）＝-0.5log（1-x），对于0≤x＜1。信息测量法计算自变量权重通过平均所有p！次序得出。

7.临界值法

临界值法也称Criticality［18］，是由Azen等人于2001年提出在多元回归模型中测量自变量重要性的一个新的方法。自变量的临界值定义为对于一个给定的总体中，自变量被纳入到最佳子模型中的概率。确定自变量的临界值有以下四步：

（1）用bootstrap法从原始数据中抽取一个大样本。

（2）对抽取的每个数据集，根据同一准则选择最佳模型。

（3）根据选择的最佳模型分别得出2p-1个子模型的相对频率。

（4）得出每个自变量被纳入最佳模型的概率即临界值。

临界值法测量自变量重要性不是依赖于原始数据组成的特定模型，而是平均了由原始数据的重复抽样组成的最佳模型中某个自变量被纳入出现的概率值作为该自变量的重要性值，因此也算作平均秩次方法。

前提条件与对策理论的基础

线性回归模型中，基于平均秩次的方差分解法估计自变量重要性的方法的前提条件是当自变量之间存在多重共线性以及自变量的重要性排序独立且未知的情况下，求解自变量重要性除临界值以外都是以模型的选择和模型的拟合优度为条件，即基于平均秩次的方法将模型的R2分配给每个自变量的非负贡献，也就是要求所有自变量的重要性的估计值之和必须等于模型的R2，且每个自变量的重要性估计值必须非负。而临界值法的测量是不依赖模型的选择而是考虑了所有可能的模型而不是自变量的次序。

基于平均秩次的方差分解法这个概念是由Lindeman、Merenda和Gold三人于1980年首先提出，后续的几种方法除临界值法都是在此方法上加以改变。但事实上，大量的文献指出基于平均秩次的思想与Shapley在1953年提出在对策理论中计算效益分配问题的思想是一致的。Cox于1985年推导出对策理论中求解Shapley value的数学公式和基于平均次序的方差分解法求自变量重要性是等同的［4］。Stufken指出分层划分法中的独立成分I也是等同于Shapley Value［29］。Feldman［10，30］和Ortmann［31］也指出PMVD是对策论中求解Shapley Value的一个实例。优势分析和LMG法本质上和Shapley Value法是等同的，都是将模型的R2通过平均秩次的方法分配给每个自变量。所以对策理论的Shapley Value法提供了另一个通过平均秩次计算自变量相对重要性的具有深渊意义的理论方法。对策理论解决的问题就是在一项多人参与工作中，找到一种方法将合作产生的效益公平、有效的分配给每个参与者，实际上就是对参与者贡献的排序，这与线性回归模型中求解自变量重要性的问题是同构的。对策理论的基础是在一个n人参与的联盟中，找到一个能够代表每个联盟贡献的特征函数v，v（S）表示参与者联盟S（联盟中成员的个数为s）的贡献，让参与者i进入联盟S，计算参与者i的边缘贡献｛v（S∪i）-v（S）｝，考虑到参与者进入联盟的次序和组成联盟的人数不同，平均参与者i组成的所有可能的子集的边缘贡献，在1953年，Shapley在文献中基于四个公理给出了计算公式-v（S）］，后来Roberts也给出了详细的数学推导，使得计算公式也作为公理而被广泛应用。

总结和展望

本文总结了几种近年来在不同领域文献中出现的当自变量存在多重共线时基于平均次序的方差分解法估计自变量的重要性的方法。基于平均次序的方差分解法估计自变量的重要性方法的提出使得回归模型的应用更加广泛。这种方法是基于Achen于1982年提出三种重要性中的离散重要性，即各自变量对因变量变异的贡献［32-33］。这些方法都克服了传统方法的一些缺陷，因为它们考虑了所有可能的子模型。另外对策理论中的Shapley Value的求解是基于一些准则和公理推导得出，这使得用Shapley value估计自变量的重要性更为准确和可信［33］。但是，基于平均次序的方差分解法都是首先找到一个度量的方法，然后计算了自变量在不同组合序列中以不同的次序进入模型求出其度量准则然后求其平均，这就决定了平均次序方法对计算机的要求较高。平均次序方法对于中等的自变量的个数的相对权重的计算也需要较大的计算量，所以当自变量的个数太多时，例如超过30，这种方法便不可用了。另外，在样本中，如果自变量的个数超过观测个数时，这种方法也不可用了［33］。当自变量的个数较大时，计算量也增加的很快，这也限制了这种方法的进一步使用［32-33］。因此，当自变量存在多重共线时，如何在构建统一的期望准则下准确、简单地估计自变量重要性的方法仍是一个有待研究的问题。

1.代鲁燕，张波，黄启风.相对权重法在线性模型自变量相对重要性中的估计及其应用.中国卫生统计，2013，30（1）：19-22.

2.张波，代鲁燕，黄启风.logistic回归中自变量相对重要性的相对权重估计.中国卫生统计，2012；29（2）：191-195.

3.Lindeman RH，Merenda PF，Gold RZ.Introduction to Bivariate and Multivariate Analysis：Scott，Foresman，1980.

4.Cox LA.A new measure of attributable risk for public health applications Management Science，1985，31（7）：800-813.

5.KruskalW.Correction to“relative importance by averageing over orderings”.The American Statistician，1987a，41：341.

6.KruskalW.Relative Importance by Averaging Over Orderings.The A-merican Statistician，1987b，41（1）：6-10.

7.Soofi ES.A generalizable formulation of conditional logitw ith diagnostics.American Statistical Association，1992，87：812-816.

8.Soofi ES.A framework formeasuring the importance of variables w ith applications to management research and decisionmodels.Decision Sciences，2000，31（3）：1-31.

9.孙红卫，王玖，罗文海.线性回归模型中自变量相对重要性的衡量.中国卫生统计，2012，29（6）：900-902.

10.Feldman B.Relative importance and value，2005.

11.Grömping U.Estimators of Relative Importance in Linear Regression Based on Variance Decomposition.The American Statistician，2007，61（2）：139-147.

12.Grömping U.Variable Importance Assessment in Regression：Linear Regression versus Random Forest.The American Statistician，2009，63（4）：308-319.

13.Grömping U.Relative Importance for Linear Regression in R：The package relaimpo.Journal of Statistical Software，2006，17（1）：1-27.

14.Chevan A，Sutherland M.Hierarchical Partitioning.The American Statistician，1991，45（2）：90-96.

15.Cuadras CM.Interpreting an Inequality in Multiple Regression.The A-merican Statistician，1993，47（4）：256-258.

16.Budescu DV.Dominance Analysis A New Approach to the Problem of Relative Importance of Predictors in Multiple Regreesion.Psychological Bulletin，1993，114（3）：542-551.

17.Budescu DV.Dominance Analysis SAS Macros.2003［cited 2012 jamuary 17］；Available from.

18.Azen R，Budescu DV，Reiser B.Criticality of predictors in multiple regression.British Journal of Mathematical and Statistical Psychology，2001，54：201-225.

19.Budescu DV，Azen R.Beyond GlobalMeasuresof Relative Importance：Some Insights from Dominance Analysis.Organizational Research Methods，2004，7（3）：341-350.

20.Azen R，Budescu DV.The dom inance analysis approach for comparing predictors in multiple regression.Psychological Methods，2003，8（2）：129-148.

21.Lipovetsky S，Conklin M.Analysis of regression in game theory approach.Applied Stochastic Models in Business and Industry，2001，17（4）：319-330.

22.Conklin M，Powaga K，Lipovetsky S.Customer satisfaction analysis：Identification of key drivers.European Journal of Operational Research，2004，154（3）：819-827.

23.Israeli O.A Shapley-based decomposition of the R-Square of a linear regression.The Journal of Econom ic Inequality，2006，5（2）：199-212.

24.Yongjun L，Liang L.A Shapley value index on the importance of variables in DEA models.Expert Systems with Applications，2010，37（9）：6287-6292.

25.Grömping U，Landau S.Do not adjust coefficients in Shapley value regression.Applied Stochastic Models in Business and Industry，2010，26（2）：194-202.

26.Weiner JL，Tang J.Multicollinearity in Customer satisfaction research：Roland Clifford，2005.

27.Theil H.How many bits of information does an independent variable yield in a multiple regression？Statistics＆Probability Letters，1987，6（2）：107-108.

28.Theil H，Chung C-F.Information-Theoretic Measures of Fit for Univariate andmultivariate linear regressions.The American Statistician，1988，42（4）：249-252.

29.Srufken J.On hierarchical partitioning.The American Statistician，1992，46：70-71.

30.Feldman B.The Proportional Value of a Cooperative Game.In：University BC，editor.First World Congress of the Game Theory Society（Games2000）；July 24-28，2000；Bilbao，Spain：Fundacion B.B.V.；July 24-28，2000.

31.Ortmann KM.the proportional value of a positive cooperative game.Mathmatical Methods of Operation Research，2000，51：235-248.

32.Johnson JW，Lebreton JM.History and Use of Relative Importance Indices in Organizational Research.Organizational Research Methods，2004，7（3）：238-257.

33.Jian B.A Review of Statistical Methods for Determ ination of Relative Importance of Correlated Predictors and Identification of Drivers of Consumer Liking.Journal of Sensory Studies，2012，27（2）：87-101.

（责任编辑：丁海龙）

*：国家自然科学基金（81172771）

1.宁波大学医学院预防医学系（315211）

2.浙江医药高等专科学校

△通信作者：沈其君，E-mail：shenqijun＠nbu.edu.cn