一种logistic回归率比估计方法的SAS实现*

高文龙刘小宁颜 虹

一种logistic回归率比估计方法的SAS实现*

高文龙1，2刘小宁1颜 虹2△

在流行病学中，对于发病率较低的疾病，OR可以作为相对危险度或率比（RR：relative risk/rate ratio）的近似估计，因此能够被用来评估某一因素风险的大小。但是，对于一些发病率较高的疾病来说，此时用OR值会高估风险大小［1］，此时宜用RR值来评估风险的大小更为合适。本文在SAS软件中利用logistic回归实现Schouten等人提出的扩充原始数据集估计率比的方法［2］，为科学工作者准确地评价某一因素对疾病的风险提供了新的思路。

参数估计方法实现的原理

对于发病率较低的疾病而言，比值比可以作为相对危险度（RR）的近似估计。因此，在logistic回归中，当得到某一因素的回归系数估计值后，便可以得到危险因素不同水平下RR的近似估计值。此时如下式（2）所示：

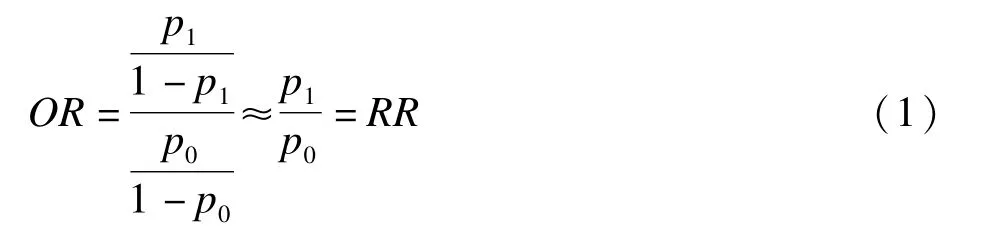
但是，很多情形下疾病的发病率较高，此时，须采用RR值来评价因素风险的大小。下面扩充数据集后采用logistic回归的方法能够直接得到某一因素RR值的精确估计。

扩充数据集估计率比的原理：Schouten等人提出了一种扩充原始数据集利用logistic回归来实现率比估计方法［2］。扩充数据集（EDS：expanded data set）的产生过程如下：在原始数据集（ODS：original data set）中每一个病例组数据复制后设置成非病例数据。此时，新的数据集由三部分构成：原始病例，原始非病例和新非病例。设ODS中病例发生的概率为p，在EDS中，观察落入上面三个部分中的概率分别是因此，在EDS中病例观察到的概率应为：

此时，在EDS中进行结局变量Y的logistic回归时：

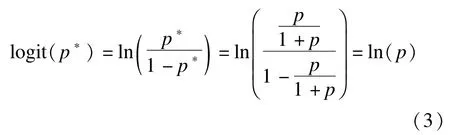
即p*的OR等于p的RR值。

SAS实现程序

设存在某一ODS，包含结局变量Y（Y＝1为病例，Y＝2为非病例）和分类自变量X1，X2，X3，…，Xn。根据EDS估计率比的原理，利用logistic回归估计这些分类变量RR值的SAS程序如下：

第一步：建立原始病例集和非病例集

data example1；set ODS；/*数据集example1中包含了原始病例集和原始非病例集*/

第二步：建立新非病例集

data example2；set ODS；

if Y＝1；/*选取结局变量为1的数据集*/

Y＝2；/*将结局变量取值由1变为2，建立了新非病例集example2*/

第三步：合并两个数据集，组成扩充数据集example。

data example；set example1 example2；

第四步：利用logistic回归估计自变量X1-Xn的率比

proc logistic data＝example；/*在扩充数据集example上直接进行logistic回归*/

class X1 X2...Xn；/*设定分类变量X1...Xn */model Y＝X1-Xn；/*实现logistic回归，得到EDS中X1-Xn的OR值及其可信区间*/run；

由此，可得ODS中X1-Xn的RR值及其可信区间。值得注意的是，在SAS中，logistic回归分类变量X默认的参照取值为last，如果改变参照值，可在class语句后增加参照设定语句/para＝REF REF＝（first or last）。如果设定回归的类型，如前进法，后退法等，可在第四步中增加/SELECTION参数进行选择。

实例分析

以2005年西安交通大学医学院开展的农村初级卫生保健服务项目（2001-2005年）终期调查的家庭数据为例，分析婴幼儿两周腹泻患病率和产前检查率的风险因素。具体的抽样方法和调查内容在相关的研究中己经做了详细的描述［4］。调查结果显示，三岁以下儿童两周腹泻患病率为7.37%，孕产妇产前检查率为98.03%。本研究选取婴幼儿两周腹泻患病和产前检查为结局变量，利用ODS的logistic回归、EDS的logistic回归和ODS的log二项回归三种方法来探索腹泻患病率和产前检查率的风险因素。本研究仅对两个结局有显著性（α＝0.05）的部分变量（腹泻患病率：民族和儿童年龄；产前检查率：家庭社会经济状况和母亲教育年限进行单因素回归分析，来比较三种方法评估因素对结局风险的差异，对于多因素回归分析方法与之相似。

本研究数据分析采用SAS9.1.3软件进行。ODS的logistic回归、EDS的logistic回归和ODS的log二项回归三种方法评估结果见表1。由表1可见，三种方法估计的民族和儿童年龄对两周腹泻患病率的风险差别并不很大，但ODS的Logistic回归严重高估了家庭社会经济状况和母亲教育年限对产前检查率的风险，但EDS的Logistic回归与ODS的log-binomial回归对该结局的估计结果相近。

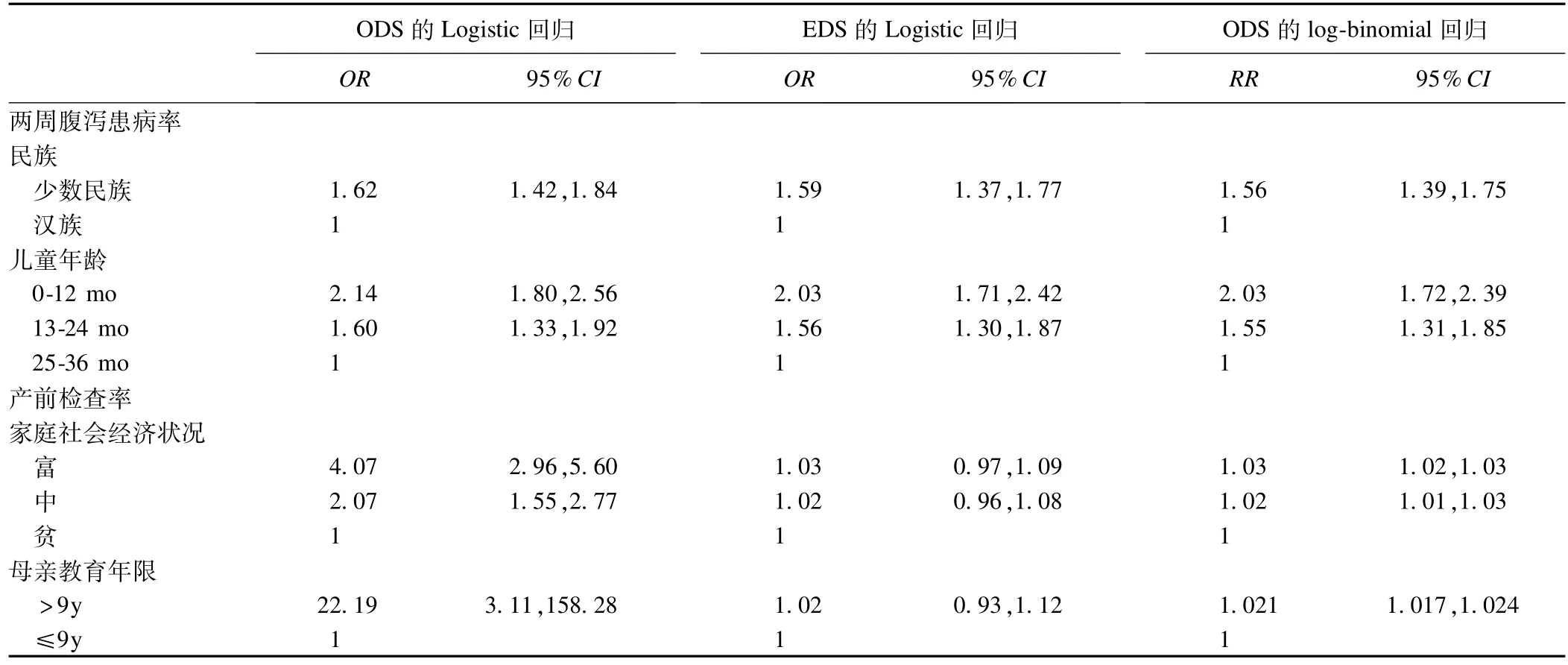
表1 利用ODS的logistic回归，EDS的logistic回归和ODS的log-binom ial回归估计婴幼儿两周腹泻患病率和产前检查率的风险

讨 论

在流行病学调查中，logistic回归分析由于能够很容易得到患病风险的近似估计值OR，因此得到广泛的应用。但是，OR值评估因素的患病风险一般认为疾病的患病率应该小于0.10［5］。当这个条件不满足，即疾病的患病率＞0.10，此时，直接利用Logistic回归分析结果来评价因素的患病风险并不恰当，它能高估该因素风险的大小［1］。此时，计算RR值来评估患病风险的大小更为准确。王静等人的研究推荐采用Cox回归方法来获得RR值［5］。Poisson回归［6］和log-binomial回归方法［7］也能够获得因素的RR值估计。但是利用Cox风险回归和Poisson回归估计RR值，有时会出现预测的概率出界问题［8］，而且它们能够使得估计参数的标准误太大，尤其是疾病的患病率很高的时候［3］；log-binomial回归估计RR值时，当自变量中具有连续性变量的时候，往往会导致模型不能收敛［7］。但是，对于概率出界问题在logistic回归分析中一般不会出现，连续性变量导致模型不收敛的问题在logistic回归中发生率较log-binomial回归更低。本文提供了一种直接利用logistic回归来获得因素的RR值的估计方法，并提供了SAS实现的程序。这个研究为丰富统计方法实现的途径增添了新的内容。

1.Localio AR，Margolis DJ，Berlin JA.Relative risks and confidence intervals were easily computed indirectly from multivariate logistic regression.JClin Epidemiol，2007，60（9）：874-888.

2.Schouten EG，Dekker JM，Kok FJ.Risk ratio and rate ratio estimation in case-cohort design：hypertension and cardiovascularmortality.Stat Med，1993，12（18）：1733-1745.

3.Skov T，Deddens J，Petersen MR，et al.Prevalence proportion ratios：estimation and hypothesis testing.Int JEpidemiol，1998，27（1）：91-95.

4.Gao W，Dang S，Yan H，et al.Care-seeking pattern for diarrhea among children under 36 months old in ruralwestern China.PLoSOne，2012，7（8）：e43103.doi：10.1371/journal.pone.0043103.

5.王静，朋文佳，何倩，等.患病率比PRR和优势比OR的关系.中国卫生统计，2012，29（1）：149-150.

6.ZocchettiC，ConsonniD，BertazziPA.Estimation of prevalencerate ratios from cross-sectional data.Int JEpidemiol，1995，24（5）：1064-1065.

7.叶荣，郜艳晖，杨笠，等.log-binomial模型估计的患病比及其应用.中华流行病学杂志，2010，31（5）：576-578.

8.Yu B，Wang Z.Estimating relative risks for common outcomeusing PROC NLP.ComputMethods Programs Biomed，2008，90（2）：179-186.

（责任编辑：丁海龙）

*：国家自然科学基金（81230016）；兰州大学中央高校基本科研业务费专项资金（lzujbky-2014-156）

1.兰州大学公共卫生学院（730000）

2.西安交通大学医学部公共卫生学院（710061）

△通信作者：颜虹