医疗机构单病种付费研究*

新疆大学数学与系统科学学院（830046） 黄雪毅吴 迪 吴黎军

医疗机构单病种付费研究*

新疆大学数学与系统科学学院（830046） 黄雪毅△吴 迪 吴黎军

目的对单病种付费方式进行深入研究，建立合理的结算模型，并确定各病种相应的结算标准。方法对各病种的实际费用数据进行统计分析和分布拟合，根据已经建立的结算模型，利用医疗机构收支平衡来确定各病种的结算标准。结果得到了4个典型病种的结算标准，这些结算标准大约都位于费用期望的70%左右，比原有的单病种限额标准更具合理性。结论本文中的结算方式具有一定的优越性，可以在一定程度上制约医疗费用的不合理增长，使广大患者受益。

单病种付费 分布拟合 结算标准

单病种付费是通过统一的疾病诊断分类，科学地制定出每一种疾病的定额偿付标准，社保机构按照该标准与住院人次向定点医疗机构支付住院费用，使得医疗资源利用标准化。单病种付费操作比较简单，既避免了医疗单位滥用医疗服务项目、重复项目和分解项目，防止医院小病大治，又保证了医疗服务质量，在实际应用中有一定优势［1-5］。

单病种限额结算是单病种付费的一种结算方式，是指对单一病种从确诊入院经检查、治疗到治愈出院限定最高医疗费用。如果治疗费用低于最高限额的，则按照实际费用支付；如果治疗费用超出最高限额，超出部分将由医院来承担［1，6］。如果限额以上费用不予报销，管理虽然简单，但是医疗机构可以通过患者来对医保部门施加压力已达到提高限额的目的，理论上也不科学。如果对超出部分予以适当报销，就可以最大可能避免道德风险和减轻医保部门压力，控制医疗费用的增长。此外，考虑到新疆公布的25类单病种的限额可能都来自经验谈判，其合理性有待实际检验，因此我们有必要从数学上来对单病种的结算方式进行深入探讨，以期望得到一个更为合理的结果。

本文提供了一种新的单病种付费结算方式，利用对2010年1-10月的乌鲁木齐市13家定点三级医院医保数据的统计分析，旨在给出在此结算方式下若干常见病种的结算标准，并与《办法》中公布的限额标准作对照，供有关部门参考。

资料与方法

1.数据来源

从乌鲁木齐市社保局获得的2010年1-10月的13家定点三级医院医保数据，主要包括各医院各病种病人的住院总费用、个人自付费用、各类报销费用、性别、年龄、疾病类型、科室、药品费用、手术费用、材料费等信息。

2.统计方法

采用Excel软件对上述费用数据进行甄别筛选，删除错误记录、不合实际要求的信息，通过把各疾病住院天数大于100天的样本删除来剔除异常值。并利用SAS 9.2软件计算各病种费用的分位数，把各病种费用在其99%分位数以上或在其1%分位数以下的样本删除，并对各病种费用数据进行统计分析。

结算模型的建立以及结算标准的确定

1.结算模型的建立

对于某个单病种来说，其住院总费用包括两大部分：个人自付费用和报销费用。个人自付费是在保险协议中不能报销的某些医疗费用，由病人自行承担；而报销费用则由医保部门和医疗机构双方结算。下面我们着重对报销费用的结算进行研究，提供如下结算方式：

设某个病种的报销费用（即住院总费用减去个人自付费用）为x，此病种的结算标准为d，医保部门实际支付的费用为z。我们建立如下结算模型：当报销费用x低于结算标准d时，医保部门支付给医疗机构的费用为d，结余部分归医院所有；而当报销费用x高于结算标准d时，医保部门首先支付给医疗机构费用d，然后对于超过结算标准d的部分再分段给予一定比例的报销，剩余部分费用由医疗机构自行承担，即：

采用此结算模型一方面可以适当降低结算标准，操作较为简便；另一方面，由于在结算标准以上部分还给予了适当比例的报销，相比传统的单病种按人次定额支付或限额支付方式来说，此结算办法可以进一步提高医疗机构的服务积极性，使广大患者受益。

2.结算标准的确定

对于结算标准d的确定，我们从医疗机构方面来考虑。对医疗机构来说，其从医保部门获得的报销费用函数为：

而其需要支出的费用函数为：

从而医院从保险部门获得的净收入费用函数应为：

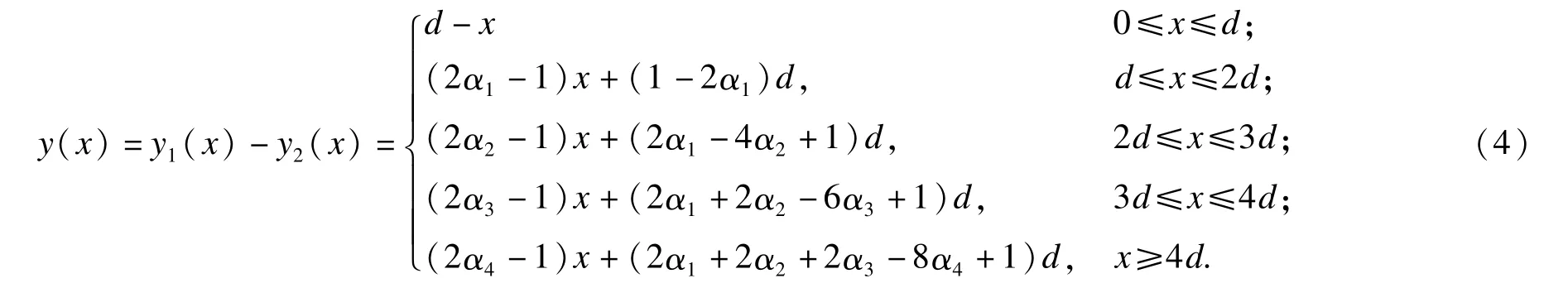
结算标准d应使医疗机构从医保部门获得的报销费用与其支出的费用收支平衡。不妨设某病种的报销费用x所服从理论分布的密度函数为f（x），则要使医院收支平衡，有：

即：

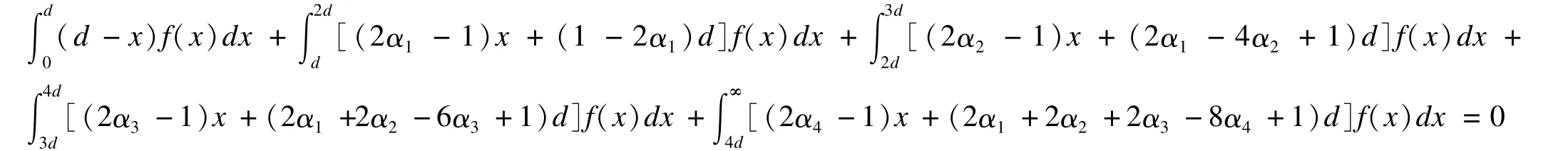
如果知道某病种的费用分布密度函数，以及事先给定的该病种在结算标准以上部分费用的分段报销比例α1，α2，α3，α4，就可以根据上式求出结算标准d。

结算模型的实际应用

1.数据的选取

我们选取乌鲁木齐市医疗保险定点三级医院样本量在400以上的6个常见病种的住院报销费用进行研究。这里样本的住院报销费用都是按照人次来统计的，报销费用剔除异常值后的病种基本信息如下表1：

2.报销费用分布的拟合及参数的估计［7-10］

我们利用SAS 9.2软件对上述6个病种的报销费用进行分布拟合，发现有4个病种的费用通过了三参数正态分布检验，即它们的住院报销费用是服从三参数对数正态分布的，这4个通过分布检验的病种的检验情况见下表2：

表1 6个病种报销费用剔除异常值后的基本信息

表2 4个病种的三参数对数正态分布检验情况（显著水平为0.05）

我们知道，三参数对数正态分布X～Λ（θ，μ，σ2）的密度函数为：

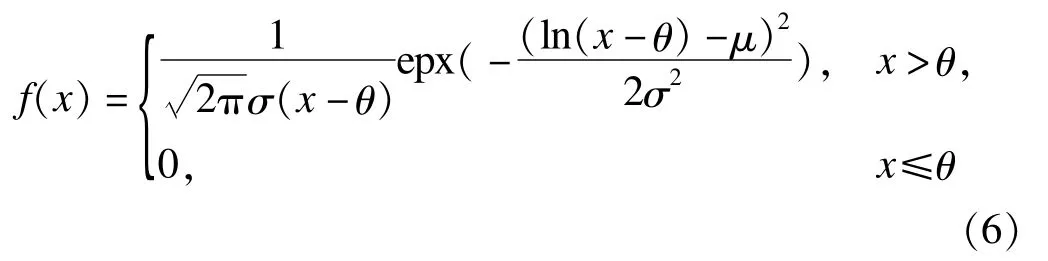
其中θ为移位参数。则随机变量X的数学期望及方差分别为：

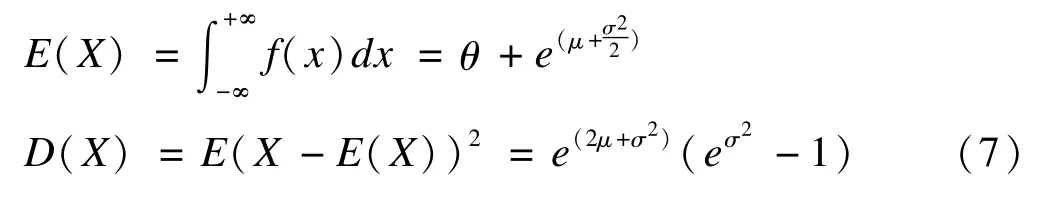
在利用SAS 9.2软件进行分布拟合的过程中，其对上述三个参数也同时进行了估计，如下表3：

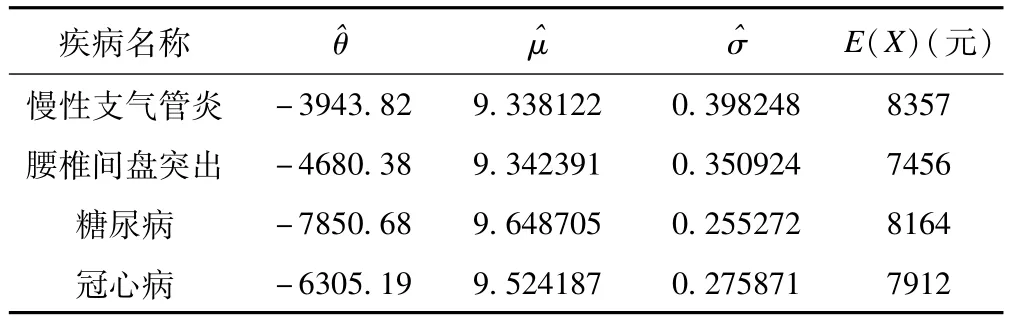
表3 各病种报销费用的参数估计以及理论期望

由于其他2个病种暂时未找到合适的分布拟合，因此下面我们着重对这4个病种的付费结算进行深入研究，可以为其他病种提供一个参考。

2.具体病种结算标准的计算

对于结算模型（1）中结算标准以上部分费用的分段报销比例的选取，我们提供以下两种标准供参考：

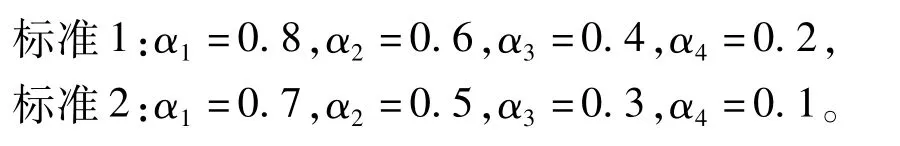
这两种标准是具有一定实际意义的，对于超过结算标准越多的部分，给予的报销比例越低，这样能更好地控制医疗费用的增长。

现在将表3中4个病种的参数分别代入到（6）式中，求得各病种的分布密度函数，然后再将各密度函数和两种标准下的报销比例代入到（5）式中，并利用Matlab编制程序搜索得到各病种的结算标准如下表4：

表4 各病种的结算标准

从表4中可以看出，原有的单病种限额标准很不合理，对于慢性支气管炎、糖尿病、冠心病来说，原有标准过低；而对于腰椎间盘突出来说，原有标准过高，已经超过了费用均值。而在我们的结算模型中，发现当报销比例取标准2时，结算标准大约都位于费用均值的70%左右，赵福慧建议取均值的75%作为标准［11］，可见前面得到的结算标准有一定的合理性。

讨 论

本文对单病种付费方式进行深入研究，相比较传统的单病种支付方式，我们给出了一种较为科学的单病种结算方式。针对此结算方式，又给出了一种合理确定结算标准的理论方法，并应用此方法解决实际中的单病种报销费用支付问题，得到了4个典型常见病种的结算标准，与原有的限额标准进行了对比，结果比较满意。

单病种付费虽然有很多优点，但其覆盖面比较有限，只能限定在一些诊断明确、治疗方案成熟的单纯性病种。而国际疾病诊断分类有3万余条，不可能一一制定相应的付费标准。因此，只能利用此付费方式来解决一些典型病种的费用支付问题。此外，利用本文中的理论方法来确定各病种结算标准的难点之一在于费用数据理论分布的拟合，分布的拟合需要大量的费用数据作支撑，且对数据的准确性要求较高。

1.杨迎春，巢健茜.单病种付费与DRGS预付模式研究综述.中国卫生经济，2008，27（6）：66-70.

2.杜乐勋，吴广华，朱玉久，等.医院单病种付费概念与内容、历史和现状以及政策建议.中国医院管理，2007，27（9）：23-25.

3.杨树东，张晓，沈其君.我国医疗保险制度中实行单病种付费的思考.东南大学学报，2006，25（1）：47-49.

4.吴阿元，李一平，张咏杨，等.按病种付费在医保费用结算中的实践和探究.中国卫生经济，2004，23（9）：38-39.

5.李洪云.单病种结算控制患者住院费用研究.科学与财富，2011，6：7-8.

6.兰迎春，陈丽.单病种限价收费：遏制过度医疗的新举措.中国卫生事业管理，2006，22（6）：333-335.

7.金丕焕主编.医用SAS统计分析.上海：上海医科大学出版社，2000，17-23.

8.张占忠.三参数对数正态分布的参数估计.高校应用数学学报，1993，8（4）：386-395.

9.张明，柏绍光.对数正态分布参数估计的积分变换矩法应用.人民长江，2011，42（19）：21-23.

10.杨婷，王玉贵，杨波，等.球坐标变换对医疗费用结构的拟合和预测研究.中国卫生统计，2011，28（3）：266-267.

11.赵福慧.医疗保险结算办法的实践和探究.中国总会计师，2008，61：92-93.

（责任编辑：刘 壮）

新疆大学重点项目（编号：XJU-SRT-Z11003）；国家自然科学基金资助项目（11361058）

△通信作者：黄雪毅，E-mail：tsjshxy＠163.com