曲线模型在细菌性痢疾发病趋势预测中的应用及评价

六安市金安区卫生局卫生监督所（237006） 邹奇志

曲线模型在细菌性痢疾发病趋势预测中的应用及评价

六安市金安区卫生局卫生监督所（237006） 邹奇志

每一种疾病不论发生、发展及转归，都有各自的演变规律，如果能很好地了解和掌握这些规律，势必对各种疾病的预防起到干预和调控作用。近年来很多学者运用数学模型对特定人群的死亡率、发病率等进行了预测。目前预测疾病发病趋势的方法有很多，如定性预测的控制图、Bayes概率法、定量分析的多元逐步分析法、回归分析预测法等［1］。

回归分析预测法是分析自变量和因变量之间关系建立回归方程作为预测模型。常见的回归方程有线性趋势回归方程、多项式趋势回归方程、指数趋势回归方程等，筛选一个合适的回归方程尤为重要。

细菌性痢疾是一种严重危害健康的肠道传染病，是全球的公共卫生问题，每年发病人次估计达1.65亿，约110万病例死亡，死亡率居感染性腹泻之首［2］，因此该病防治仍然是传染病控制工作中的重点。现对六安市细菌性痢疾流行概况进行分析并根据回归方程对疫情趋势进行短期预测。

材料与方法

1.数据来源 疫情资料来源于“中国疾病预防控制信息系统”六安市2005-2011年疾病监测信息报告；当年人口资料依据安徽省人口统计年鉴。

2.模型的筛选与评价

（1）模型的筛选

回归方程选择方法，除观察散点图外，通过计算一阶差分、二阶差分、三阶差分和百分比差分来筛选。当时间序列的一阶差分完全相同时，即（Y2-Y1）＝（Y3-Y2）＝（Y4-Y3）＝…＝（Yn-Yn-1），可认为线性趋势方程能完全拟合该时间序列［3］。当时间序列的二阶差分完全相同时，即［（Y3-Y2）-（Y2-Y1）］＝［（Y4-Y3）-（Y3-Y2）］＝…＝［（Yn-Yn-1）-（Yn-1-Yn-2）］，可认为二次曲线趋势方程能完全拟合该时间序列。当时间序列的三阶差分完全相同时，即［（Y4-Y3）-（Y3-Y2）-（Y2-Y1））］＝［（Y5-Y4）-（Y4-Y3）-（Y3-Y2）］＝…＝［（Yn-Yn-1）-（Yn-1-Yn-2）-（Yn-2-Yn-3）］，可认为三次曲线趋势方程能完全拟合该时间序列。当时间序列的百分比差分完全相同时，即（（Y2-Y1）/Y1）×100%＝（（Y3-Y2）/Y2）×100%＝…＝（（Yn-Yn-1）/Yn-1）×100%，则可以认为指数曲线趋势方程能完全拟合该时间序列。

（2）模型的评价

根据筛选的结果，建立一个相对较好的曲线模型，对数据进行拟合，最后利用回归预测模型计算预测值，并对预测值进行综合分析，确定最后的预测值。

3.资料分析

所有数据用SPSS 16.0和excel 2007进行分析统计。

结 果

1.流行情况

（1）流行强度和时间分布

2005-2011年六安市累计报告细菌性痢疾5422例，发病率8.93～17.74/10万，年均发病率为12.73/10万之间，差异有统计学意义（χ2＝371.87，P＜0.001），其中2005年处于前部高端（17.74/10万），此后逐年下降，2009年到底点（8.93/10万），此后又逐年上升至2011年后期高端（16.34/10万），总体呈扁“U”型分布，2005年至2009年呈下降趋势；2009年至2011年呈上升。每月均有病例发生，发病高峰在每年6～9月，占总发病例数的67.83%。

（2）地区分布

从发病率对比可以看出，2005-2010年霍山县的发病率位于全市前列，2011年发病率高的霍邱县24.48/10万、金安区23.81/10万。从平均发病来看，最高的是霍山县，平均发病率28.06/10万，区间为16.24/10万～42.77/10万；其次是裕安区，平均发病率19.07/10万，区间为12.37/10万～34.23/10万。

从发病数对比可以看出，2005-2009年裕安区的发病占全市构成比前列，2010年构成比居于前位的是霍邱县和舒城县，2011年构成比居前位的是霍邱县。从历年发病数合计构成来看，最高的裕安区，占20.84%；第二位的是霍邱县，占19.77%。

（3）人群分布

病例年龄主要集中在0.5～4岁，占27.96%，5～9岁，占6.75%。男性为主，男女性别比为1.6∶1。从职业来看，病例主要集中在农民、散居儿童和学生，构成比分别是38.64%、28.35%和14.05%。

2.回归模型的建立与评价

（1）年发病率差分计算

计算一阶差分值多大于零，百分比差分值多大于零且波动较大，而三阶差分值在零轴上下随机波动，变异相对较小，因此相对于线性和指数回归，三次多项式趋势回归方程可能更加适合发病数据。

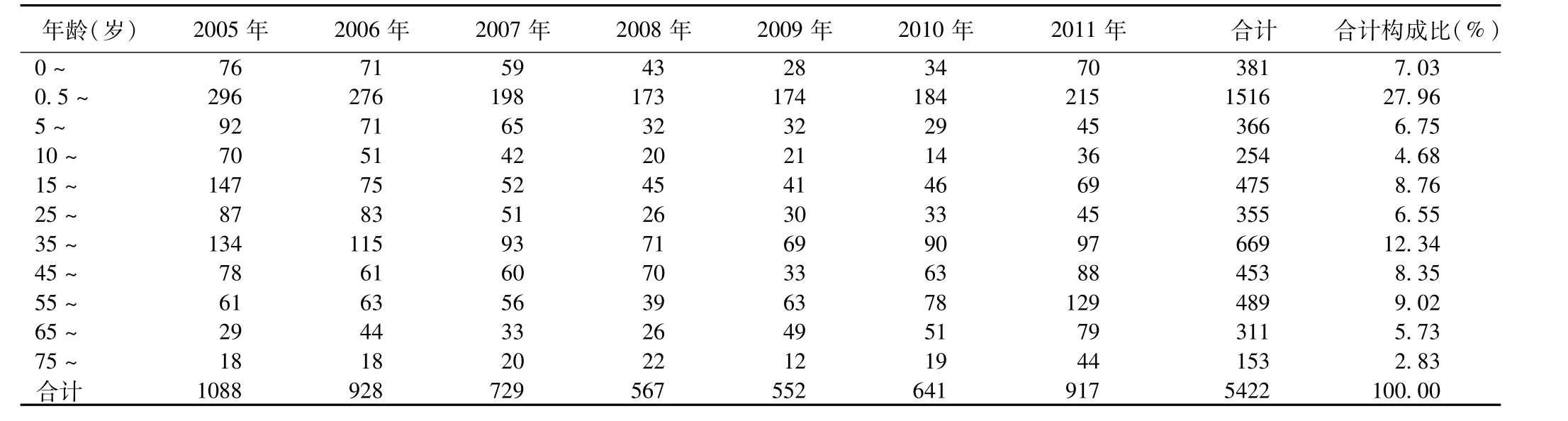
表1 历年各年龄段发病情况

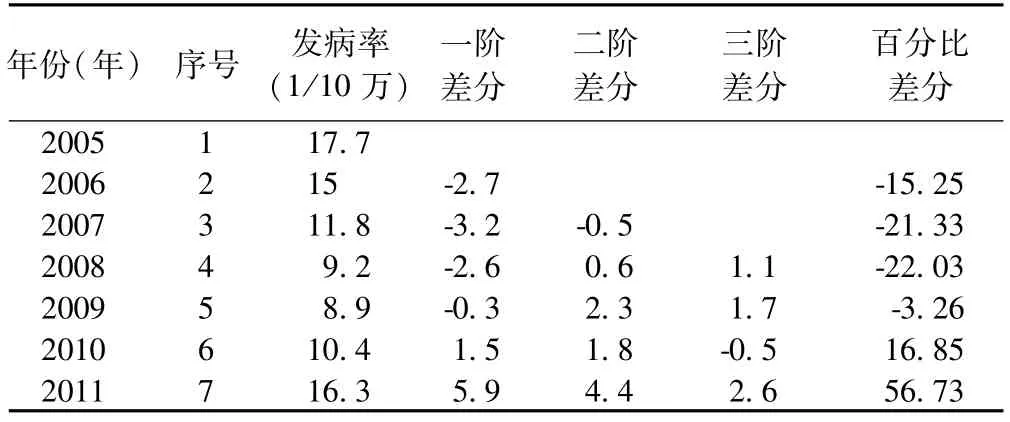
表2 差分值计算结果

（2）建立和检验曲线模型

以序号为自变量，历年发病率为因变量，分别计算线性和曲线回归模型的参数，分别建立线性和曲线模型进行拟合，对建立的指数曲线预测模型公式计算相关指数R2。对应用的指数曲线预测模型方程计算相关指数，可见三次曲线R2＝0.998最大，有统计学意义（F＝521.54，P＜0.001），说明三次曲线拟合效果较好（见表3，图1）。

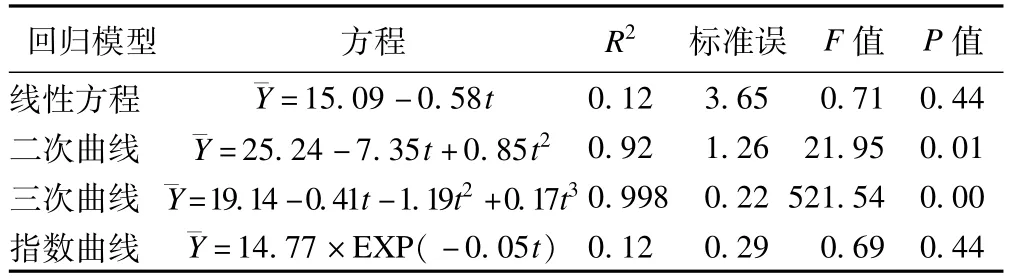
表3 线性和曲线回归模型参数估计

3.模型的应用

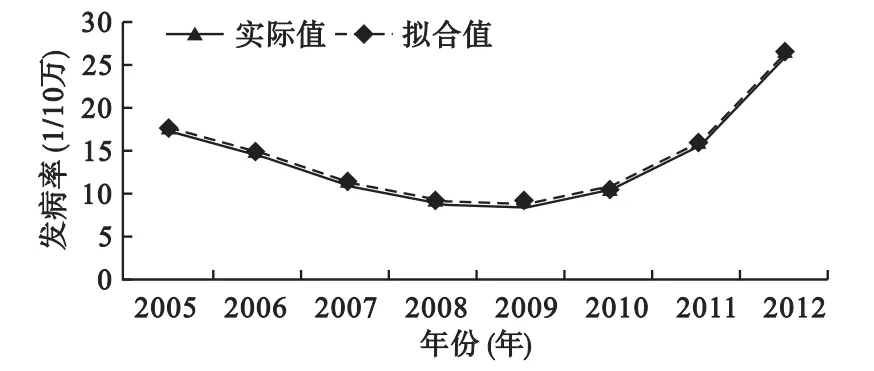
图1 实际值与拟合值比较和2012年预测

讨 论

1.六安市细菌性痢疾发病率先降后升，防控形势不容乐观。由于其流行因素复杂，多年来细菌性痢疾是影响居民健康和生活质量的主要传染病之一［4］。2009年后发病率又呈上升态势，因此依然是防控重点。当地应根据夏秋季节发病高峰的特点，针对农民、散居儿童、学生等重点人群，进一步采取以切断传播途径为主的综合性防治措施，加强传染源的管理，改进基础卫生设施建设，提高城乡自来水普及率及增强群众卫生意识等。

2.ARIMA时序模型、Markov模型、流行控制图法等都可用于预测细菌性痢疾发病趋势，但以上方法应用相对繁琐。回归分析预测法在实际工作中应用比较广泛，我们将这一方法应用于传染病的发病趋势预测中，能在对既往传染病发病数据的分析基础上对今后一定时间内的发病趋势作出预测。本文应用简单方法得出拟合方程，拟合效果较好。

3.传染病的发病情况受很多因素影响，实际情况千变万化，预测结果与实际结果之间可能存在不同，如何修正，正是预测者对这种主客观原因及其影响的判断，也是预测者能力和水平之所在［4］，这就要求在运用这一方法开展预测过程中不能机械，应灵活运用，注意了解影响预测结果的偶然情况，及时对预测结果进行适当修正，才能使预测结果更接近实际，为实际防病工作服务。

1.董选军，贾伟娜.ARIMA时间序列和BP神经网络在传染病预测中的比较.现代实用医学，2010，22（2）：142-147.

2.卫生部疾病预防控制局.痢疾防治手册.北京：人民出版社，2006：11-12.

3.王全意，主编.疾病监测信息报告管理系统数据分析手册.北京：中国协和医科大学出版社，2009.

4.蒲柳艳.舟山市细菌性痢疾发病率的指数曲线趋势预测.浙江预防医学，2005，17（5）：21-22.

（责任编辑：郭海强）