多孔材料刚度对微铣削加工稳定性的影响

王黎辉，韩锦锦，刘志强

(江苏科技大学机械工程学院，江苏镇江212003)

随着人类社会和科学技术的快速发展，工业上对高精度、高质量和高性能精密和超精密微小零件的需求与日俱增.目前材料去除成形的传统工艺方法为车削、铣削、刨削等.微铣削加工技术作为铣削加工的一种方法，相比于宏观铣削，最大的不同就在于加工尺度方面.微观铣削的加工尺寸在毫米级，特征尺寸在微米级，铣刀直径在0.5 mm以下.研究表明微铣削加工技术具有三维加工能力、较高加工精度和加工成本低等优点，在加工微小零件方面具有独特的优势.但是，微铣削由于主轴转速较高和采用微型铣床、微铣刀等因素的影响使系统更易发生颤振.目前，国内外学者在微观铣削加工颤振方面的研究还非常有限.这主要因为微观铣削和宏观铣削加工机理不尽相同，必须从微铣削的特点和切削机理出发建立适用于微铣削颤振的力学模型和预测模型等.

多孔材料是一种新型的多功能材料，它集物理性能与结构特征于一体，具有高比强度、高比刚度、高刚韧性、密度小、孔隙率高和耐撞击等多功能特性［1］.从材料微观结构规则程度特点看，多孔金属材料可以分为有序和无序两大类，前者主要指蜂窝材料(点阵或栅格材料)，后者主要指泡沫材料.随着材料在制备工艺方面的发展和材质性能的提高，多孔金属材料被广泛应用于航空航天、交通运输、建筑工程、机械工程、电化学工程和环境保护工程等领域.另一方面，多孔金属材料内部微结构的存在使其在切削加工时表现出刚度分布不均的特点，这必将引起颤振的发生.近年来国内外学者在多孔金属材料研究方面已取得了很大的进展，并逐渐扩展到了微观领域，但成果主要侧重于多孔金属材料的制备方法、力学性能和破坏机理等方面，很少涉及多孔金属材料在切削加工过程中微结构对力学性能的影响等方面的研究，更没有适用于这些材料的微切削力预测模型，所以这些问题亟待解决.

从国内外学者对宏观切削和微观切削的研究成果来看，为了控制颤振，必须采用科学方法来选择合理的切削参数，最常用的方法就是绘制切削系统的稳定性叶瓣图.该方法首先需要建立系统的动力学模型，目前能够用于切削过程动力学建模的方法主要有以下几种:经验建模法［2］、解析建模法［3］、数值模型法和力学建模法［4］.力学法目前切削力预测应用最广，其最大的优点就是计算时间短.

高速微铣削加工过程通常采用微小机床加工零件，而微小机床的质量小、固有频率较普通机床高，这将有利于机床在较宽主轴转速范围内运行而不发生振动;同时在微铣削加工过程中切削力较小，更适用于多孔材料的加工.文中主要针对多孔材料等效刚度计算方法和微铣削加工稳定性影响因素展开研究.

1 多孔材料高速微铣削动力学建模

现以有序多孔钛合金材料为研究对象，参照均匀致密材料宏观切削原理，并假定刀具为刚性体进行分析.这里把多孔钛合金材料看作是由正六边形单元体周期性排布而成的微结构体，可以通过建立周期性单元胞模型来分析其力学性能与微结构的关系.将多孔钛合金材料加工工件微铣削过程简化为相互垂直的两自由度弹性——阻尼系统，则加工系统动态微铣削过程的动力学模型［5］如图1.

工件的振动可以表示为:

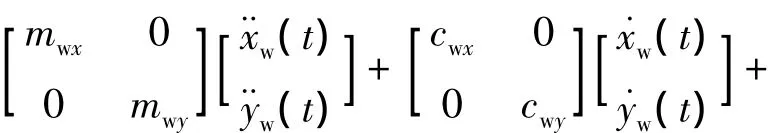
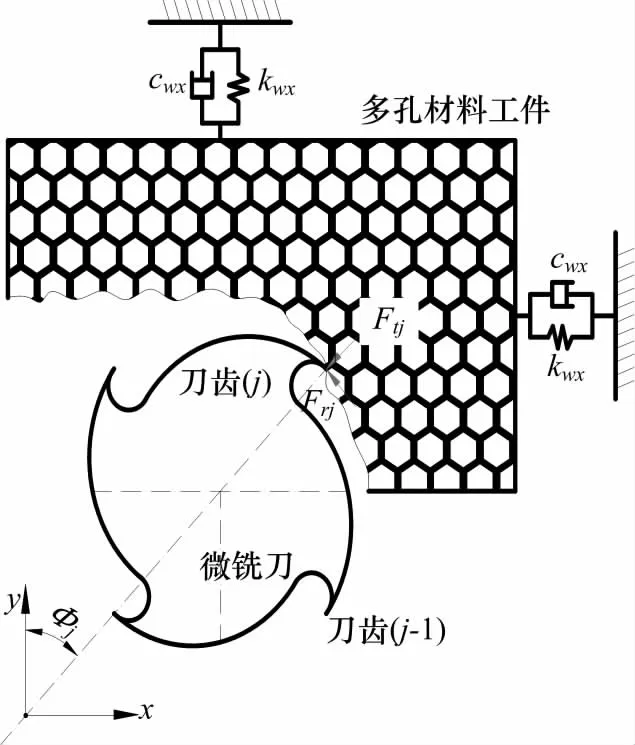
图1 多孔材料微铣削模型Fig.1 Model of porous materials micro-milling

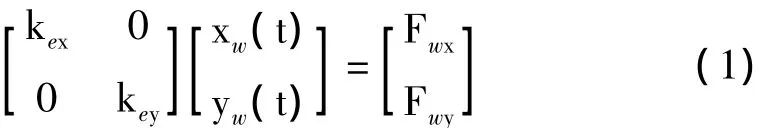
式中:kex，key分别为工件在x和y两个方向的等效刚度，主要是考虑多孔钛合金材料本身的微结构对工件整体刚度的影响;xw，yw分别为工件在x和y两方向的位移;mwx，mwy，Cwx，Cwy，Fwx，Fwy分别为工件在x和y两个方向的质量、阻尼和力.

式(1)也可写成矩阵形式:

其中:M，C分别为多孔金属工件的模态质量和模态阻尼，K为等效模态刚度矩阵;Ks(φj)为系数矩阵，由参考文献［6］可推导得:

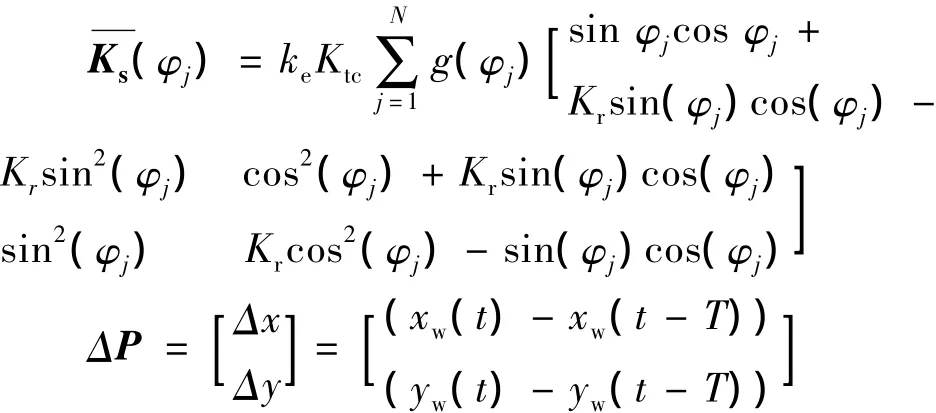
式中:Ktc为切向切削力系数;Krc为径向切削力系数;Kr=Krc/Ktc.

2 多孔材料等效参数

2.1 多孔金属材料力学性能

多孔材料的宏观力学性能同时受到构成材料的力学特性和细观孔洞构造特征的影响.在微铣削加工过程中，由于材料的各向异性和结构的非连续性，导致其切屑形成机理与传统致密金属材料切削加工有很大不同，研究表明［7］材料内部的微结构对工件加工质量和表面完整性会产生很大的影响;在高速平板冲击作用下，多孔泡沫金属的变形曲线主要经历3个阶段:弹性段、平稳段和致密段.

另外，复杂的微结构还会使多孔金属材料的切削加工性能变差，这不仅会诱导刀具发生微振动，而且会使刀具与切屑接触区域的温度大大增加，缩短切削刀具的使用寿命.Tutunea-Fatan等人［8］利用断续切削理论和变形切削理论，对该现象进行了分析讨论，多孔金属材料在微铣削加工过程中会出现闭孔现象.变形切削理论认为:加工过程中材料的金属晶粒会在刀具切削刃的压力作用下，被推挤到邻近的孔洞中，然后在工件的表面形成一层包含很少或没有孔隙的材料，即导致闭孔的现象;闭孔现象将会改变多孔材料原有的特性.研究表明［9］:采用负前角刀片并在低温环境下进行切削加工，可改善闭孔现象的发生，同时还发现延长工件的预冷时间能够得到较为均匀孔隙分布的加工表面.另外，多孔金属材料的性能与孔隙率、孔的大小和排布有直接的关系，孔隙率、孔的大小和排布不同，多孔材料表现出的性能就不同.

2.2 等效刚度的确定

目前确定多孔材料等效参数通常的做法是:将多孔材料中每个离散的胞体等效为连续的实体，建立相应的计算公式或者通过实验测定求得多孔材料的等效弹性模量、等效弯曲刚度、等效剪切刚度等参数.在等效变换过程中，首先要建立多孔材料的等效简化模型，通过分析单元胞壁的变形确定其力学性能，等效梁模型就是最常见的研究模型之一.

实际上，可以通过间接的方法求得等效刚度，即先计算等效模量的方法来确定.综合目前对周期性多孔材料的研究，用于等效模量的计算方法主要有均匀化方法［10］、G-A 细观力学方法［11-12］、拉伸能量法，还有弯曲能量法［13］等.

现针对正六边形周期多孔材料等效弹性模量的计算方法进行说明，其正六边形单元胞模型如图2.

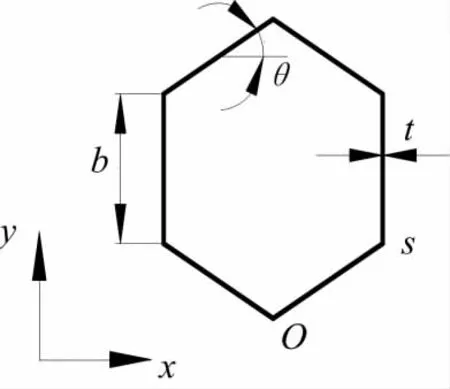
图2 单元胞模型Fig.2 Unit cell model

图2中b和t分别为单元胞胞壁的长度和厚度，θ为胞壁夹角，此处θ=30°.

1)均匀化方法

均匀化方法是求解等效弹性参数广泛使用的一种方法，采用该方法来计算上述单元胞等效弹性张量的表达式为:

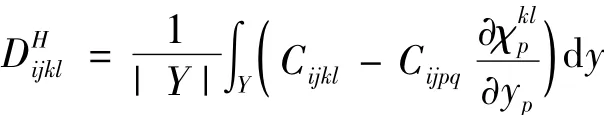
式中各符号含义见文献［10］.

2)G-A细观力学法

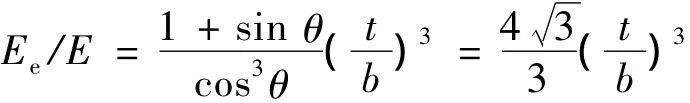
在此基础上，Chen等人［12］做了相应的改进(此处称之为G-A改进力学法):

该式反映了泊松比vs对等效弹性模量的影响.

3)拉伸能量法

采用拉伸能量法得到的正六边形单胞等效弹性模量为:

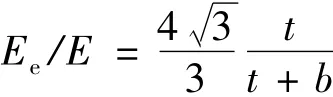
4)弯曲能量法

上述的均匀化方法、G-A细观力学法、拉伸能量法都无法反映体胞尺寸效应对单元胞力学性能的影响.戴高明等人［13］借用细长梁模型提出了弯曲能量法，有效建立了等效弹性模量与单元胞尺度缩放因子n的相互关系，表达式为:

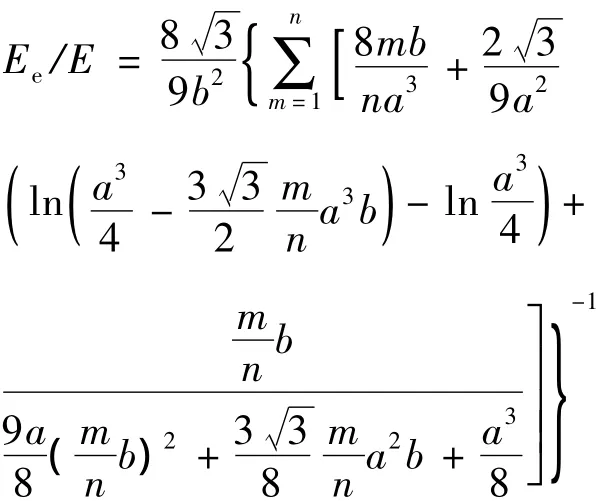
其中，a=t/n.

会上，玉溪供电局作为公司财务共享服务建设试点单位进行了财务共享建设先行先试经验交流，介绍了财务共享服务建设基本情况和内外部流程梳理情况，向大会作了财务共享服务建设报告，并就试点过程中存在的问题提出建议。随后，楚雄供电局作了利润中心建设及实施效果分享；文山供电局作了风险协同管控平台运用经验分享；大理供电局作了财务信息化建设运用经验分享；公司财务部还向大会宣贯了“基于多维精益核算的一键式报表合并平台”。

由以上4种方法可知，均匀化方法得到的等效弹性模量仅取决于不同材料相的体分比与弹性模量，而没有涉及微结构单胞壁长与壁厚相关的量;弯曲能量法虽能够反映等效抗弯刚度与尺度缩放因子的相对关系，但该方法比较复杂;G-A细观力学法和拉伸能量法虽然无法反映体胞的尺寸效应，但所得到的等效弹性模量依赖于微结构单胞壁长与壁厚，可以直观有效地用于单元胞参数对多孔材料等效刚度的影响研究;另外G-A细观力学法还可以分析泊松比［14］的影响，由此可见G-A细观力学法更适合于研究多孔材料等效刚度与壁长和壁厚的关系.

等效弹性模量确定之后，即可获得等效刚度.上述模型在各方向的等效弯曲刚度为(I为正六边形单元胞的惯性矩):

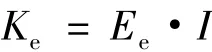
2.3 单元胞参数对等效刚度的影响

对于正六边形周期多孔材料，单元胞胞壁长度和壁厚大小可能会影响材料的力学性能.本小节将基于G-A细观力学法来分析胞壁长度b和壁厚t对等效刚度的影响.

1)胞壁长度b和壁厚t影响

由图3可知，等效刚度随着胞壁长b值的增大逐渐减小，而随着t值的增大而逐渐上升，胞壁长b一定时，壁厚越厚，材料刚度越大，越不容易变形;壁厚不变时，壁长b越长，刚度越小，胞壁越容易发生弯曲变形.

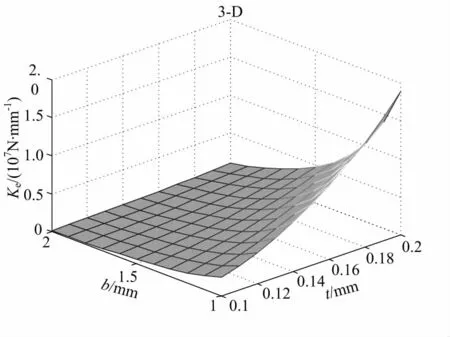
图3 b和t对等效刚度影响Fig.3 Effect of b and t on equivalent stiffness

2)泊松比vs影响

图4绘制的G-A细观力学法和G-A改进力学法曲面图对比说明:泊松比vs对等效刚度有影响，在一定程度上会降低材料的刚度;不过两种方法图形形状大致相同.

总之，多孔材料的刚度随胞壁长度和厚度的不同而不同，胞壁厚度增加，刚度有明显的增强;胞壁长度越大，刚度会减小，同时两者的影响程度也不同.此外，材料刚度在一定程度上还受泊松比的影响.

图4 vs对等效刚度影响Fig.4 Effect of vson equivalent stiffness

3 微铣削稳定性

微铣削过程失稳现象是当今众多学者重点研究的对象之一，为了能够有效地控制和改善颤振的发生，就需要对微铣削过程进行稳定性分析和预测.目前国内外学者采用的方法概括起来主要有三大类，即时域法、频域法和实验法.文中将运用全离散法［2］来对图1系统进行稳定性分析.

3.1 全离散法求解过程

对于刚性刀具-柔性工件单自由度加工系统，其系统动力学模型可表示如下:

式中:T=60/(NΩ);cw=2ξωn，ξ为阻尼比，ωn是自然圆频率为:

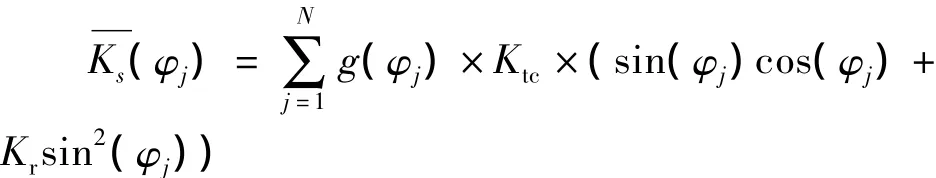
令p(t)=mwx˙(t)+x(t)·cw/2，并记X(t)=，则式(3)可变换为以下形式:

X(t)=R0X(t)+Q(t)X(t)-Q(t)X(t-T)式中:R0表示时不变系统的常数矩阵;Q(t)为周期矩阵，且Q(t)=Q(t+T).此处矩阵R0和Q(t)分别为:

现以六边形多孔钛合金材料工件微铣削稳定性叶瓣图的绘制为例.采用三齿微铣刀进行加工，切向铣削力系数为Ktc=986.3MPa，Kr=0.4125，K=6.5×105N/mm，w=813×2π(rad/s)，ξ=0.0103，所得稳定性叶瓣如图5.

图5 稳定性叶瓣图Fig.5 Stability lobes diagram

3.2 参数对稳定性的影响

保持其他参数不变，依次改变刚度值、固有频率和阻尼率.

1)刚度k对稳定性的影响

保持其他参数不变，改变刚度k的值，使其满足关系k1＜k2＜k3，所得仿真结果如图6.

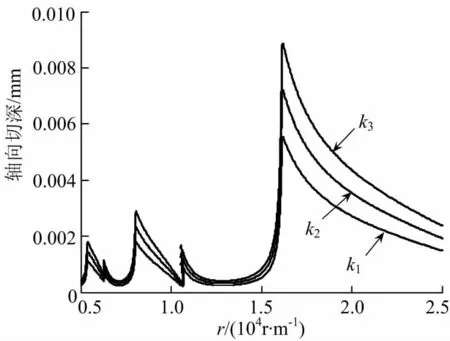
图6 刚度k对稳定性的影响Fig.6 Effect of k on stability

由图6可知，刚度值由k1变化到k3稳定性图会向上偏移，也就是说:刚度值大，得到的轴向切深较大，即有更大的加工稳定域.由此可知稳定切削深度随刚度值的增大而增大，所以刚度值的大小对稳定性的影响很大，不可忽视.对于多孔金属材料而言，必须选择合理的方法来较为准确地计算等效刚度值，确保稳定加工.

2)固有频率ωn对稳定性的影响

保持其他参数不变，改变固有频率ωn的值，使其满足关系ω1＜ω2＜ω3，所得多孔材料的稳定性结果如图7.

图7表明稳定性叶瓣图随着固有频率的增大不断向右偏移，但波谷几乎保持不变，也就是说稳定切深保持不变.

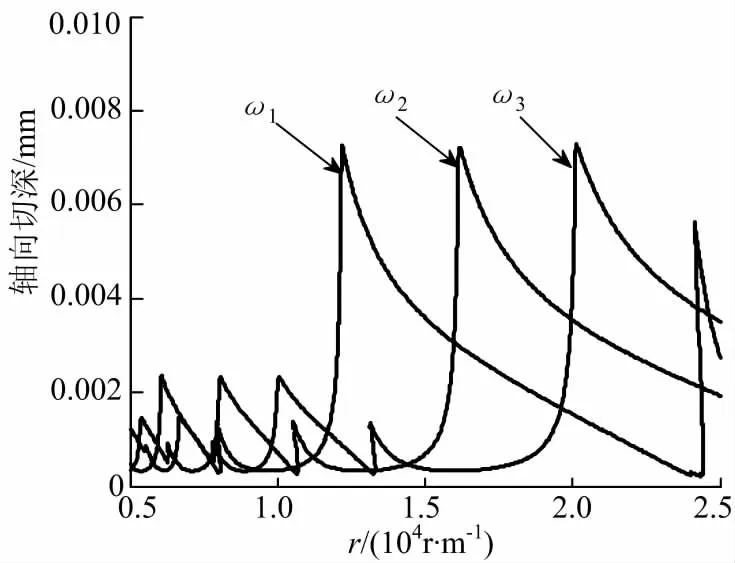
图7 固有频率ωn对稳定性的影响Fig.7 Effect of ωnon stability

3)阻尼率ξ对稳定性的影响

同样保持其他参数不变，改变阻尼率ξ的值，使其满足关系ξ1＜ξ2＜ξ3，所得多孔材料的稳定性结果如图8.

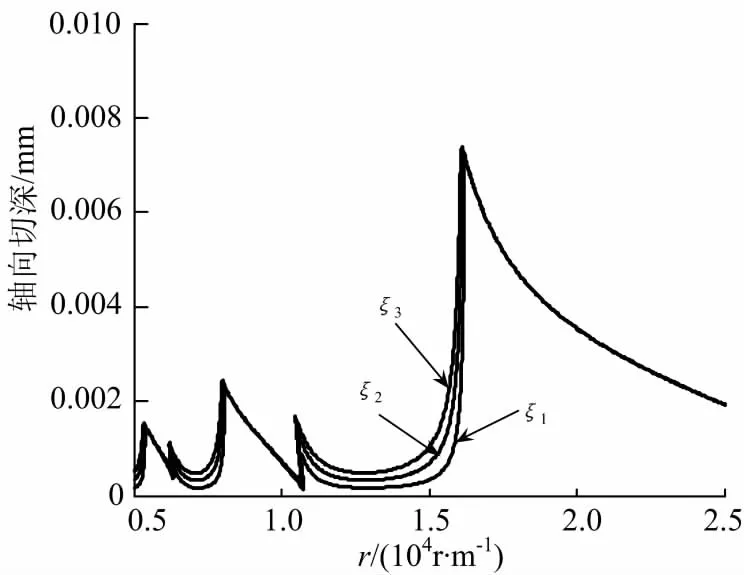
图8 阻尼率ξ对稳定性的影响Fig.8 Effect of ξ on stability

从图8可以看出阻尼率值越大，对应更大的轴向切深，加工稳定域就会越大.

综上可知，多孔材料的稳定性叶瓣图会受到模态参数的影响，增大刚度和阻尼率都会使其向上偏移，即增大了稳定铣削区域;而改变固有频率则会使叶瓣图横向移动.

4 结论

文中对多孔金属材料微铣削加工稳定性进行了研究，分析了刚度等参数对加工稳定性的影响，结果表明:刚度对加工稳定性有很大影响.多孔材料内部复杂的微结构常常会影响其力学性能，正六边形单元胞胞壁的长度和厚度会导致材料的刚度发生变化，胞壁厚度增加，刚度有明显的增强，而胞壁长度越大，刚度会减小，同时两者的影响程度也不同;此外，材料刚度在一定程度上还受泊松比的影响.所以，多孔材料等效刚度直接决定于等效单元胞模型的胞壁长度和壁厚，不同胞壁长度和壁厚的多孔材料工件在加工过程中表现不同的特征，进而影响零件最终的使用性能.总之，多孔材料的力学性能与其孔洞构造特征密不可分，在计算多孔材料等效刚度时选择合理的方法和单元胞参数对材料的稳定加工至关重要.文中的研究为进一步提高多孔材料微铣削加工稳定性提供了理论依据，因此具有一定的理论参考价值.

References)

［1］ 卢天健，何德坪，陈常青，等.超轻多孔金属材料的多功能特性及应用［J］.力学进展，2006，36(4):517-535.Lu Tianjian，He Deping，Chen Changqing，et al.The multi-functionality of ultra-light porous metals and their applications［J］.Advances in Mechanics，2006，36(4):517-535.(in Chinese)

［2］ Ding Ye，Zhu Limin，Zhang Xiaojian，et al.A fulldiscretization method for prediction of milling stability［J］.International Journal of Machine Tools＆Manufacture，2010，50:502-509.

［3］ Gonzalo O，Beristain J，Jauregi H，et al.A method for the identification of the specific force coefficients for mechanistic milling simulation［J］.International Journal of Machine Tools＆Manufacture，2010，50:765-774.

［4］ Gao Ge，Wu Baohai，Zhang Dinghua，et al.Mechanistic identification of cutting force coefficients in bullnose milling process［J］.Chinese Journal of Aeronautics，2013，26(3):823-830.

［5］ 杨建中，李江威，屈文晓，等.铣削加工过程稳定性分析［J］.中国机械工程，2013，24(3):360-365.Yang Jianzhong，Li Jiangwei，Qu Wenxiao，et al.A-nalysis of milling process stability［J］.China Mechanical Engineering，2013，24(3):360-365.(in Chinese)

［6］ Altintas Y.Manufacturing automation-metal cutting mechanics，machine tool vibrations and CNC design［M］.London:Cambridgel Universty Press，2002:33-36.

［7］ Popov J K B，Dimov S S，Pham D T，et al.Micromilling:material microstructure effects［J］.Journal of Engineering Manufacture，2006(1):1807-1813.

［8］ Tutunea-Fatan O R，Fakhri M A，Bordatchev E V.Porosity and cutting forces:from macroscale to microscale machining correlations［J］.Journal of Engineering Manufacture，2011，225:619-629.

［9 ］ Schoop J，Effgen M，Balk T J，et al.The effects of depth of cut and precooling on surface porosity in cryogenic machining of porous tungsten［J］.Procedia CIRP，2013(8):57-362.

［10］ Hassani B，Hinton E.A review of homogenization and topology optimization I-homogonization theory for media with Periodic structure［J］.Computers and Structures，1998，69(6):707-717.

［11］ Gibson L J，Ashby M F.Cellular solids:structures ＆properties［M］.Oxford:Pergamon Press，1988.

［12］ Chen D H，Ozaki S.Analysis of in-plane elastic modulus for a hexagonal honeycomb core:Effect of core height and proposed analytical method［J］.Composite Structures，2009，88:17-25.

［13］ 戴高明，张卫红.周期性多孔材料等效杨氏模量的尺度效应研究［J］.中国科学 G辑，2009，39(7):955-963.

［14］ 魏勤，卫婷，董师润，等.超声波法测量金属材料的杨氏模量和剪切模量［J］.江苏科技大学学报:自然科学版，2012，26(1):27-30.Wei Qin，Wei Ting，Dong Shirun，et al.Ultrasonic determination of Young′s and shear modulus of metal materials［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2012，26(1):27-30.(in Chinese)