Hadron multiplicities in p+p and p+Pb collisions at the LHC∗
WANG Hong-Min(王宏民),HOU Zhao-Yu(侯召宇),and SUN Xian-Jing(孙献静)
1Physics Department,Academy of Armored Forces Engineering of PLA,Beijing 100072,China
2Physics Graduate School,Shijiazhuang Railway Institute,Shijiazhuang 050043,China
3Institute of High Energy Physics,Chinese Academy of Sciences,Beijing 100049,China
Hadron multiplicities in p+p and p+Pb collisions at the LHC∗
WANG Hong-Min(王宏民),1,†HOU Zhao-Yu(侯召宇),2and SUN Xian-Jing(孙献静)3
1Physics Department,Academy of Armored Forces Engineering of PLA,Beijing 100072,China
2Physics Graduate School,Shijiazhuang Railway Institute,Shijiazhuang 050043,China
3Institute of High Energy Physics,Chinese Academy of Sciences,Beijing 100049,China
Experiments at the Large Hadron Collider(LHC)have measured multiplicity distributions in p+p and p+Pb collisions at a new domain of collision energy.Based on considering an energy-dependent broadening of the nucleon’s density distribution,charged hadron multiplicities are studied with the phenomenological saturation model and the evolution equation dependent saturation model.By assuming the saturation scale has a small dependence on the 3-dimensional root mean square(rms)radius at different energy,the theoretical results are in good agreement with the experimental data from CMS and ALICE collaboration.The predictive results in p+p collisions atof the LHC are also given.
Hadron multiplicities,Negative binominal distribution,Gluon saturation
I.INTRODUCTION
Charged hadron multiplicities in relativistic heavy ion collisions are of great significance as its variables are very sensitive to the underlying mechanism involved in the nuclear collisions[1].These can provide a unique opportunity to test the predictions of quantum chromo-dynamics(QCD)and understand the partonic structure of the colliding nuclei.Among thevariables,thepseudo-rapiditydistributionandnegativebinominal distribution(NBD)are two important and interesting variablequantitiestobestudiedonbothexperimentalandtheoretical sides in recent years[2–7].
The pseudo-rapidity distribution of charged hadron is one quantity always used to investigate the particle production mechanism in high energy hadron-hadron and nucleusnucleus collisions.Since pseudo-rapidity density is sensitive to the initial conditions of system and the hadronic final state interactions,the study of the charged hadron densities at midrapidity can provide the relevant information on the interplay between hard parton-parton scattering process and soft process.The NBD is another quantity which plays major role in describing multiplicity distribution of produced charged particles.The NBD can describe well the multiplicity distribution in almost all inelastic high energy collision processes except for the data at the highest available collider energies.In this paper,the pseudo-rapidity distribution and the NBD in p+p and p+Pb collisions will be studied in the framework of the Color Glass Condensate.
At very high energies or small Bjorken-x,QCD predicts that high density gluon in a hadron wave function form a new state,the Color Glass Condensate(CGC).In this regime,the gluon density increases inside the hadron wave functions and becomes very large in comparison to all other parton species(the valence quarks),and the sea quarks are suppressed by the coupling αssince they can be produced from the gluons by the splitting g→q¯q.
Now,CGC has become an effective theory in describing the gluon content of a high energy hadron or nucleus in the saturation regime and many saturation models have been established[8–12].These saturation models can be divided into two main kinds:the phenomenological saturation model and the evolution equation dependent saturation model.The phenomenological saturation models,such as the Golec-Biernat and W¨usthoff(GBW)model[8],the Kharzeev,Levin,and Nardi(KLN)model[9],and the Kovchegov,Lu,and Rezaeian(KLR)model[10],are very simple and their dipoleproton scattering amplitude can be given by an analytic expression.The evolution equation dependent saturation models,such as the impact parameter dependent saturation model (IP-Sat)[11]and the running coupling Balitsky-Kovchegov (rcBK)model[12],are based on the DGLAP or the rcBK evolution equation and they are very useful at small Bjorkenx or high collision energy.Having studied charged particle multiplicity distribution with the GBW model[7],we will investigate charged hadron pseudo-rapidity distribution and the NBD with the phenomenological KLN model and the evolution equation dependent rcBK model,respectively.
In order to give an accurate theoretical analysis,the nucleon’s density distribution in position space,which controls the unintegrated gluon distribution(UGD)through the saturation scale Qs,must be considered.It should be pointed out that,due to gluon saturation,the width of the gluon distribution inside a nucleon should grow with collision energyThis will lead to a broadening of the nucleon’s density distribution in position space asincreases.
Thus,we consider an energy-dependent broadening of the Gaussian nucleon thickness function,and assume the saturation scale has a small dependence on the 3-dimensional root mean square(rms)radius at different collision energies[14]. The outlineof this paperis as follows.Thetheoreticalmethod is given in Sec.II and the results and discussion are given in Sec.III.
II.METHOD
For hadron-hadron collisions,the multiplicity per unit rapidity and per unit transverse area can be given by[15]
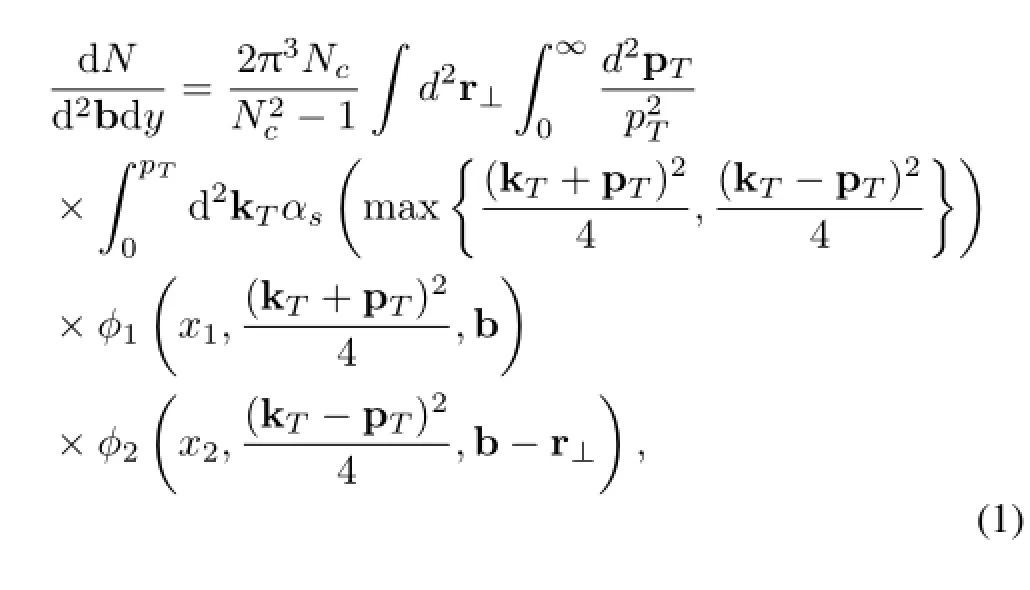
In the KLN model,φ is taken to be
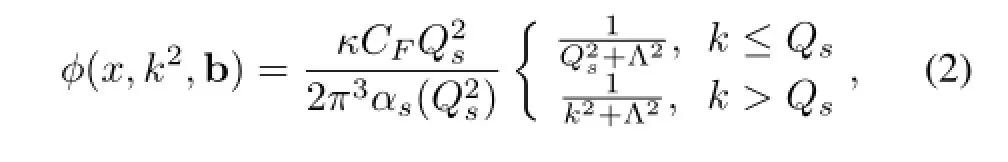
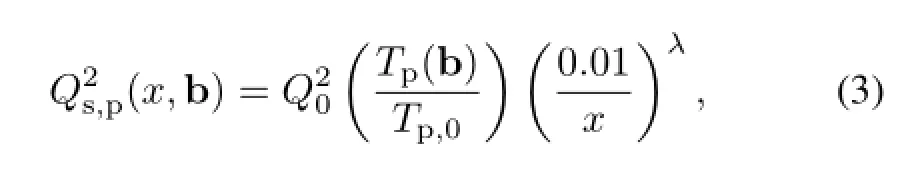
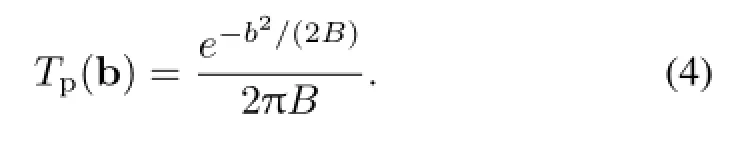
where the proton width parameter B can be computed from[13]
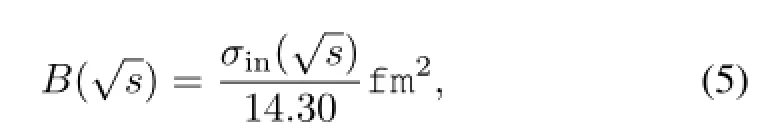

where δ=0.8[14]and the 3-dimensional rms radius rrms=In Table 1 we collect a few representative values.
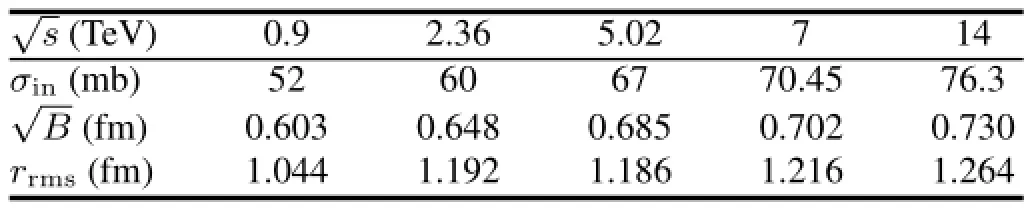
TABLE 1. The 3-dimensional rms radius for various collision energies.The values for σinat LHC energies were reported in Ref.[6,16,17]
In the rcBK model,the unintegrated gluon distribution can be obtained from the dipole scattering amplitude via a Fourier transform
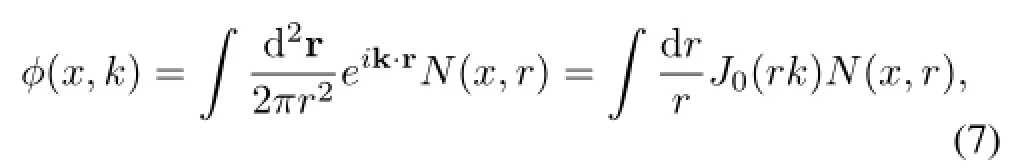
where J0is the spherical bessel function of the first kind.The dipole scattering amplitude in the rcBK evolution reads[12]
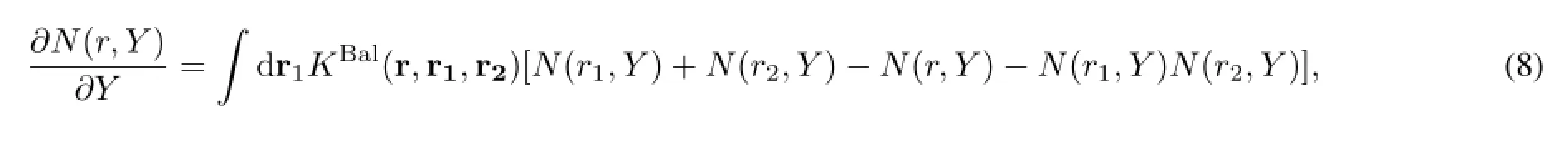
and the kernel for the running term using Balitsky’s prescription reads
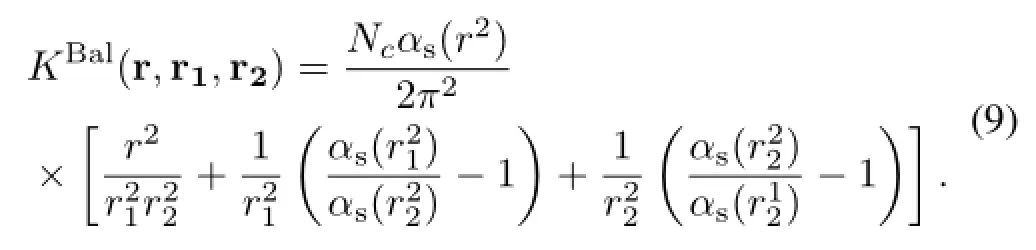
For the initial conditions,the GBW ansatz is used for the dipole scattering amplitude[8]

where γ=1 and Q2s0is the initial saturation scale squared.
Now let us take into account the negative binomial distribution.Negative binomial distribution is a general property of multi-particle production process regardless of type of colliding particles,and the negative binomial probability distribution for obtaining n charged particles in the final state is given as follows:
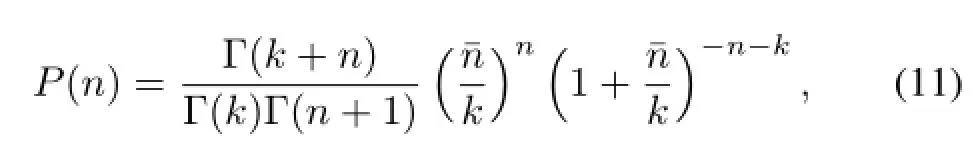
where the mean multiplicity¯n can be calculated in the framework of CGC by integrating y in Eq.(1).The quantity k, which is the fl uctuation parameter,can be estimated as a function of the saturation scale[6]
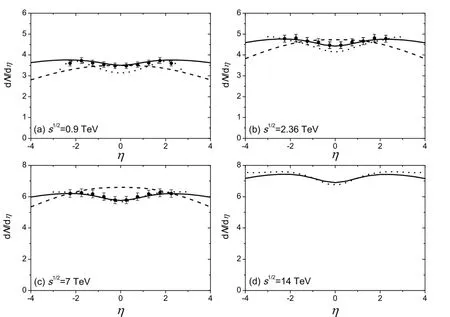
Fig.1.Pseudo-rapidity distribution of charged hadrons in p+p collisions at=0.9TeV(a),2.36TeV(b),7TeV(c),and 14TeV(d).The solid and dashed curves are the result of the KLN model with and without considering the rms radius dependent saturation scale,respectively. The dotted curves are the result of the rcBK model.The data is from CMS[2,3].
where κ′is a normalization factor.Here,in order to get an analytic expression between Qs,pand y,Qs,pis reconsidered by substitutinginto Eq.(3)as in Ref.[8].
III.RESULTS AND DISCUSSION
To evaluate the pseudo-rapidity distribution,Eq.(1)should be rewritten using the transformation

and the Jacobian can be correspondingly written as
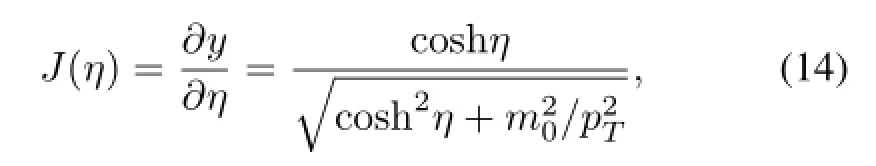
where m0is the rest mass of particle,which corresponds to the order of the scale ΛQCD.With a χ2analysis of the experimental data[18],the factor κ in Eq.(2)is equal to 0.51 and 0.89 for the theory with and without considering the rms radius dependent saturation scale,respectively.In Fig.1,the theoretical results for pseudo-rapidity distribution of charged hadrons in p+p collisions at(a),2.36TeV(b), 7TeV(c),and 14TeV(d)are shown.The solid and dashed curves are the result of the KLN model with and without considering the rms radius dependence of the saturation scale, respectively.The dotted curves are the result of the rcBK model.The experimental data comes from CMS[2,3].It is shown that the theoretical results of the KLN model considering the rms radius dependence are in good agreement with the experimental data.For the effective value of Bjorken-x in the rcBK model is 10-12< x< 0.01,it is not valid at smalor large pseudo rapidity.Thus,only the results atfit well to the data with the rcBK model.The results shown in Fig.1(d)are the predictive results for forthcoming LHC experiment at,and it is shown that the predictive results of the rcBK model are almost the same as those of the KLN model.
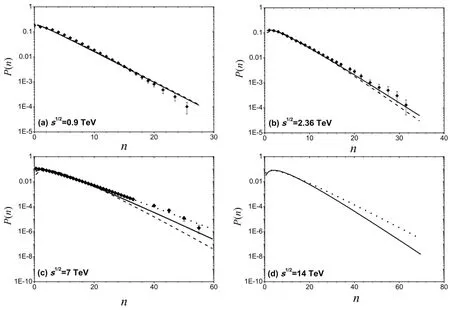
Fig.2.Negative binominal distribution in p+p collisions at =0.9TeV(a),2.36TeV(b),7TeV(c),and 14TeV(d).The symbols and lines are the same as that in Fig.1.The data is from ALICE[4].
Figure 2 shows the negative binominal distribution of a charged hadron at|η|<0.5.The symbols and lines in Fig.2 are the same as that in Fig.1.The experimental data comes from ALICE[4].The agreement is seen to be quite well for the KLN model considering the rms radius dependent saturation scale atand 2.36TeV and for the rcBK model atHere,it should be noted that the agreement is seen to be not quite well for the theoretical results of the KLN model ateven after considering the rms radius dependent saturation scale.Thus,we will give a systematic analysis of all η regions by considering the impact factor dependence of the mean multiplicity and the quantity k in the near future.
Recently,the experimental data of the charged hadron multiplicityinp+Pbcollisionsataregivenbythe ALICE collaboration[5].In order to get a further test of the theory,the pseudo-rapidity distribution of charged hadrons in p+Pb collisions are investigated.For the nuclear density distribution of Pb,we use the Woods-Saxon distribution[19]

where ρ0corresponds to the nucleon density in the center of the nucleus,R is the nuclear radius and a is the“skin depth”. The theoretical results are shown in Fig.3.The solid curve is the result of the KLN model and the dashed curve is the result that we gave in Ref.[7].The dotted and the dash-dotted curves are the results of DPMJET[20]and HIJING with the gluon shadowing parameter sg=0.28[21],respectively.It is shown that the theoretical results of the KLN model fit well to the new experimental data.
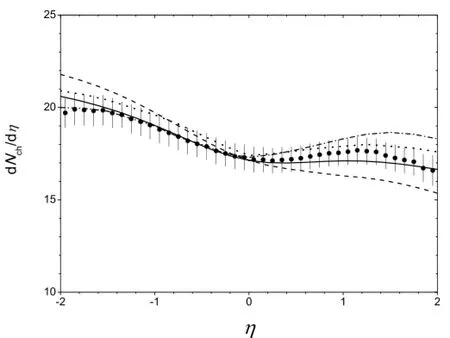
Fig.3.Pseudo-rapidity distribution of charged hadrons in minimum bias p+Pb collisions at =5.02TeV.The curves are the result of the KLN model(solid curve),the result that we gave in Ref.[7](dashed curve),the results given in Ref.[20](dotted curve) and Ref.[21](dash-dotted curve).The data comes from ALICE[5].
IV.CONCLUSION
In summary,the pseudo-rapidity distribution and the NBD of a charged hadron in p+p and p+Pb collisions are studied with the phenomenological KLN model and the rcBK model. By considering an energy-dependent broadening of the nucleon’s density distribution in position space and the rms radius dependence of the gluon saturation scale,it is found that the theoretical results are in good agreement with the experimental data from CMS and ALICE.The predictive results in p+p collisions atof the LHC will be examined b y the forthcoming experiment.
[1]Kumar A,Srivastava P K,Singh B K,et al.arXiv:hepph/1306.4185.
[2]Khachatryan V,Sirunyan A M,Tumasyan A,et al.J High Energy Phys,2010,02:041.
[3]Khachatryan V,Sirunyan A M,Tumasyan A,et al.Phys Rev Lett,2010,105:022002.
[4]Aamodt K,Abel N,Abeysekara U,et al.Eur Phys J C,2010, 68:345–354.
[5]Abelev B,Adam J,Adamova D,et al.Phys Rev Lett,2013, 110:032301.
[6]Dumitru A,Kharzeev D E,Levin E M,et al.Phys Rev C,2012, 85:044920.
[7]Wang H M,Liu J F,Hou Z Y,et al.Chinese Phys C,2013,37: 084102.
[8]Golec-Biernat K,W¨usthoff M.Phys Rev D,1999,59:014017.
[9]Kharzeev D,Levin E,Nardi M.Nucl Phys A,2004,730:448–459.
[10]Kovchegov Y V,Lu Z,Rezaeian A H.Phys Rev D,2009,80: 074023.
[11]Kowalski H and Teaney D.Phys Rev D,2003,68:114005.
[12]AlbaceteJL,ArmestoN,MilhanoJG,etal.PhysRevD,2009, 80:034031.
[13]Heinz U,Moreland J S.Phys Rev C,2011,84:054905.
[14]Armesto N,Salgado C A,Wiedemann U A.Phys Rev Lett, 2005,94:022002.
[15]Kuhlman A,Heinz U,Kovchegov Y V.Phys Lett B,2006,638: 171–177.
[16]Albacete J L,Dumitru A,Fujii H,et al.Nucl Phys A,2013, 897:1–27.
[17]Block M M and Halzen F.Phys Rev D,2011,83:077901.
[18]Wang H M,Hou Z Y,Zhang B A,et al.Int J Mod Phys A, 2010,25:1009–1018.
[19]Miller M L,Reygers K,Sanders S J,et al.Annu Rev Nucl Part S,2007,57:205–243.
[20]Roesler S,Engel R,Ranft J.arXiv:hep-ph/0012252.
[21]Xu R,Deng W T,Wang X N.arXiv:nucl-th/1204.1998.
(Received December 28,2013;accepted in revised form January 27,2014;published online August 10,2014)
10.13538/j.1001-8042/nst.25.040502
∗Supported by National Natural Science Foundation of China(No. 11247322/A050306)and Natural Science Foundation of Hebei Province (No.A2012210043)
†Corresponding author,whmw@sina.com.cn
 Nuclear Science and Techniques2014年4期
Nuclear Science and Techniques2014年4期
- Nuclear Science and Techniques的其它文章
- Development of a beta radioluminescence nuclear battery∗
- Apparatus for determining permeability of hydrogen isotopes in molten-salt
- A facile method to build a proton nanosensor with neutral to basic pH sensitive range∗
- The flow characteristics of fluid in micro-channels of different shapes∗
- An investigation on neutron induced reactions on stable CNO isotopes∗
- Readout electronics for CSR-ETF silicon strip array detector system∗
