不同微观噪音波动率度量的比较分析——基于风险管理视角

刘广应，马丽娟

（南京审计学院 金融数学与金融工程系，江苏 南京 211815）

不同微观噪音波动率度量的比较分析
——基于风险管理视角

刘广应，马丽娟

（南京审计学院 金融数学与金融工程系，江苏 南京 211815）

实证研究表明，金融高频数据常具有微观噪音，目前已产生多种能够处理微观噪音的波动率度量：二维尺度已实现波动率（TSRV）、已实现核波动率（RKV）以及已实现极差波动率（RR）。本文从风险管理角度对这些波动率度量以及已实现波动率（RV）进行比较分析，通过ARFIMA模型为波动率进行动态建模，利用偏学生分布刻画标准化收益率，建立VaR度量和预测模型。利用上证综合指数的高频数据，通过回测检验，进行实证比较分析。分析表明：基于ARFIMA高频数据波动率VaR预测模型能够准确度量VaR，TSRV、RKV、RR优于RV，TSRV优于其他波动率度量。

微观噪音；二维尺度已实现波动率；已实现核波动率；VaR；ARFIMA模型；上证综合指数

一、引言

当今金融市场发展不断深入，经济全球化不断深化，科技的迅速发展也不断冲击金融市场，刺激金融市场发展。这些变化和发展，给金融市场带来的波动持续加剧，带来了新的金融风险。2013年8月16日11点05分上海证券指数出现大幅拉升，大盘1分钟内涨幅超5%。下午2点，光大证券公告称，其策略投资部门自营业务在使用其独立套利高科技交易系统时出现问题，有媒体将此次事件称为“光大证券乌龙指事件”。该事件提示我们，金融市场监管方和金融市场参与方必须高度关注金融风险，必须进行合适金融风险管理。而要解决这一问题，则必须要准确高效地测度金融风险。

波动率的准确度量对于准确测度金融风险至关重要。随着科技发展，目前可以非常便利地存储金融高频数据，这也带来了诸多基于高频数据波动率度量方法的出现。Andersen和Bollerslev于1998年提出了已实现波动率（Realized Volatility，RV）[1]，该方法具有许多优良性质，随后吸引了众多学者研究高频数据。随着研究深入，研究者发现市场中观测误差、买卖价差等微观噪音（microstructure noise）不可忽略，在采样频率非常高时，如在1分钟、1秒钟等情形，对波动率准确度量具有很大影响，Zhang等人于2005年提出了可以克服微观噪音的二维尺度已实现波动率度量（Two-Scales Realized Volatility，TSRV）。[2]Barndorff-Nielsen等人提出了已实现核估计波动率（Realized Kernel Volatility，RKV）[3]，Parkinson提出了极差度量[4]，Chou将已实现极差波动率度量（Realized Range，RR）用于波动率预测。[5]这些方法在理论上，都能处理微观噪音影响。

金融市场监管方和参与方关心的是，如何从众多能够处理微观噪音的波动率度量方法中挑选出最优波动率度量，使得其在度量和预测金融风险VaR最为准确，如何选出最优波动率度量。邵锡栋和殷炼乾对RV与RR在VaR风险度量和预测进行了比较分析[6]，韩清和刘永刚对TSRV和RKV这两种能够克服微观噪音的波动率度量进行比较分析，得出了他们度量结果的差异[7]，他们利用中国市场数据对少数几个波动率度量进行了初步分析。Brownless和Gallo对纽约证券市场几只股票进行实证分析，较为系统地分析几种波动率度量在预测VaR上的差异，得出分析结论。[8]然而，他们得出的分析结论能否适用于中国这类不太完善的金融市场，众多处理微观噪音波动率度量在中国市场表现有无差异，是否存在最优波动率度量，这些问题都需要进行系统分析。本文针对不同微观噪音波动率度量在VaR度量和预测进行较为系统的比较研究。首先对RV、TSRV、RKV、RR主要理论性质进行回顾，然后利用上证指数对4种波动率度量进行分析，得出数据的实际特性，运用ARFIMA模型为波动率建立动态模型，利用偏学生分布描述日收益率，进一步建立VaR度量和预测模型，通过回测检验对上证指数进行实证分析，得出实证结论，最后给出应用建议。

二、波动率度量方法理论和描述性统计

将第t日的交易时间均匀地划分成I个区间，其中每一个区间的长度为则该日内的总交易时间是第t日第i个区间最后的交易价格表示为Pt,i，最高价格表示为Ht,i，最低价格表示为L（t,ii=1，2，…，I）。那么第t日的收盘价为Pt,I，该日最高价格和最低价格分别为为对数收益率，表示第t天的日收益率。

（一）已实现波动率

已实现波动率（Realized Volatility，RV）为日内各区间收益率的平方和[1]，即

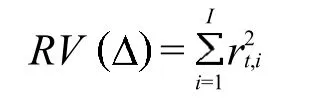
（二）二维尺度已实现波动率

二维尺度已实现波动率（Two-Scales Realized Volatility，TSRV）的基本思想是，首先利用稀疏采样降低微观噪音影响，得到已实现波动率度量，然后对不同RV进行平均来提高精度，进一步采用修正纠偏来提高估计精度。Zhang等提出的TSRV[2]，其定义如下：

（三）已实现核波动率

记第t天已实现核波动率（Realized Kernel Volatility，RKV）为RKVtH[3]，其定义为：

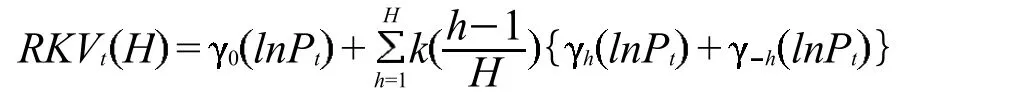
（四）已实现极差

已实现极差（Realized Range，RR）[4]定义为：

其中Ht,i表示第i个时间区间的最高价格，Lt,i为最低价格。在一定条件下，则RV与RR都是积分波动率的渐近无偏估计[1，4]，但估计方差RR是RV的1/5。由此可以看出，从理论比较上来说，RRt要比RVt效果好。[4-5]

（五）数据说明和描述统计

高频数据波动率度量与采样频率有很大的关系，Andesen和Bollerslev建议采用5分钟数据。[9]鉴于RKV度量需要利用更大量数据，其采用1分钟数据，除此以外本文主要以5分钟为采样频率对其他波动率度量进行分析。选取数据为2004年1月2日至2012年7月26日共2080天上证综合指数高频数据，数据来自于天软数据平台。本文取样本内数据为2004—01—02至2009—06—30共1332天，样本期间T=1332，用于模型的参数估计。样本外数据是2009年7月1日至2012年7月26日共748天数据，用于分析波动率度量模型的预测能力，比较分析各种模型在预测VaR上差异。上海证券交易所每一个交易日共有240分钟的交易时间，总共4个小时，也就是说I=4小时（I为每日观察值个数，为时间长度）。

为了构建合适描述数据模型，我们首先对收益率和各种波动率度量进行描述性统计分析，具体结果见表1。表中Jarque-Bera检验方法用于检验数据是否来自于正态分布，相对于给定的显著性水平，若J-B统计量的相伴概率P值小，则拒绝原假设（样本来自于正态分布）；反之，则不得接受原假设，认为数据来自于正态分布。表中Q（11）表示滞后11阶Ljung-box统计量，用于检验序列是否存在自相关，是否存在长期记忆性。表中第1行为日收益率r结果，第2—12行为波动率度量结果，其中TSRV（2）为公式（1）中G=2情形，其他符号含义类似。

根据表1，收益率序列偏度0.278小于零，峰度为3.086，表明序列具有显著左偏和尖峰厚尾特性，其J B统计量为854.626，拒绝日收益率数据来自于正态分布原假设，表明需要利用具有有偏的尖峰厚尾分布来描述收益率。Ljung-box检验Q（11）统计量结果表明，无论波动率序列本身还是对数变换后波动率序列，都具有强烈自相关性，如RV的Q（11）统计量值为4 523.940，拒绝原假设，认为存在长期记忆性。对数变化后，统计量取值都变大，表明对数变换后，长期记忆性更加明显，但收益率序列r没有表现出长期记忆性。对数变换后的波动率序列J-B统计量结果，表明可以利用正态分布描述对数波动率度量，利用正态分布可以提供统计效率，因此本文将对对数变换后的波动率进行动态建模。

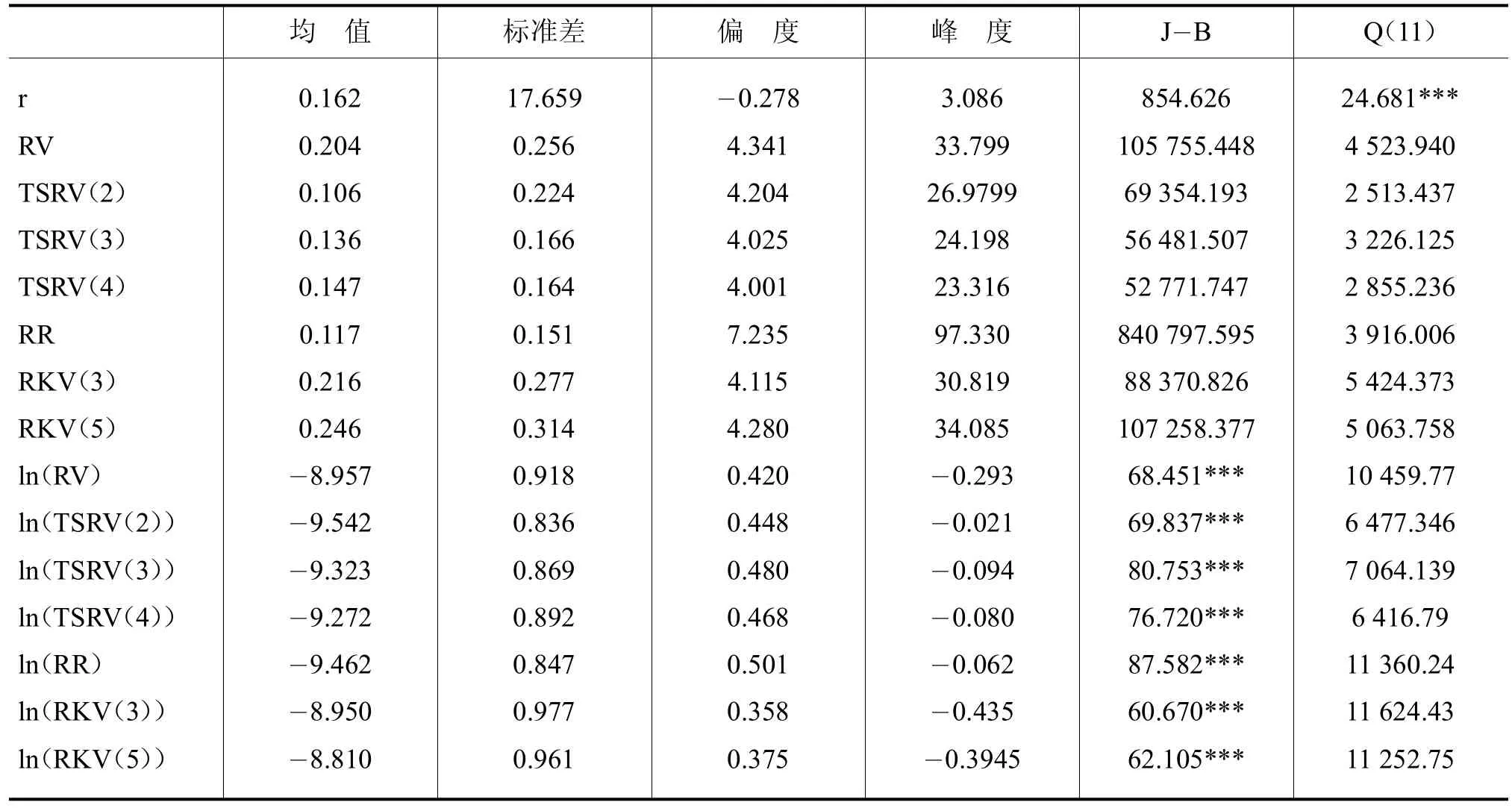
表1　上证综合指数的收益率、4种波动率估计量及其对数的描述性统计

三、高频波动率度量的ARFIMA动态模型

（一）ARFIMA模型

表1可以看出波动率的对数序列近似服从正态分布，其长记忆性比波动率本身更加显著，Andesen和Bollerslev研究表明可以利用ARFIMA模型来度量对数变换后的RV序列[9]，本文选用ARFIMA（p，d，q）为所有对数波动率进行动态建模。ARFIMA（p，d，q）即为：

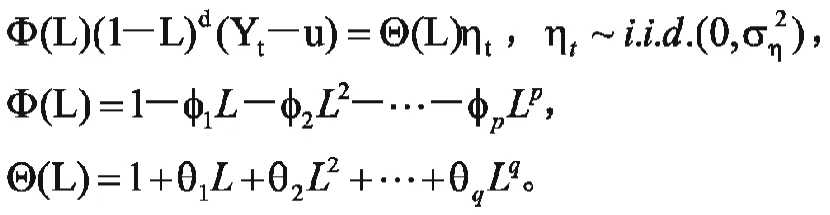
预测VaR常需要对波动率进行预测，需要先求得波动率基于第t-1天第t天的预测，在此基础上得到第t天的VaR预测值，t-1天波动率RV的一步条件预测如下：

rt为日收益率序列，常假设其为如下形式（在波动率利用RV度量情形下）：

其中，收益率序列rt的条件均值为一般将t假设成的条件方差，即表示到t 1日的所有信息汇总，zt～i.i.d0,1，2则是一个调整因子，主要是用来使zt的方差变成1。

对zt序列分布进行考虑，从表1描述统计来看，上证综合指数收益率的左偏和尖峰厚尾现象明显，且自相关性很小，而传统的假设方法如正态分布以及学生t分布都并不能很好地刻画有偏性和尖锋厚尾等现象。因此，可设Zt服从偏学生分布，且互相独立。

（二）模型阶数的确定及参数估计

本文中使用的样本内数据是2004年1月2日至2009年6月30日共1332个交易日的数据，利用ARFIMA模型分别对各种波动率的对数序列进行建模，根据AIC准则确定阶数。要使模型越准确，那么AIC值就要求越小。对各种波动率对数序列常用ARFIMA模型进行比较分析，得出最优阶数，具体估计结果见表2。表2的结果显示，各种波动率d值的范围在0到0.5之间，这验证了长记忆性的特点，并且为平稳长记忆序列，可以用来描述其对数序列。

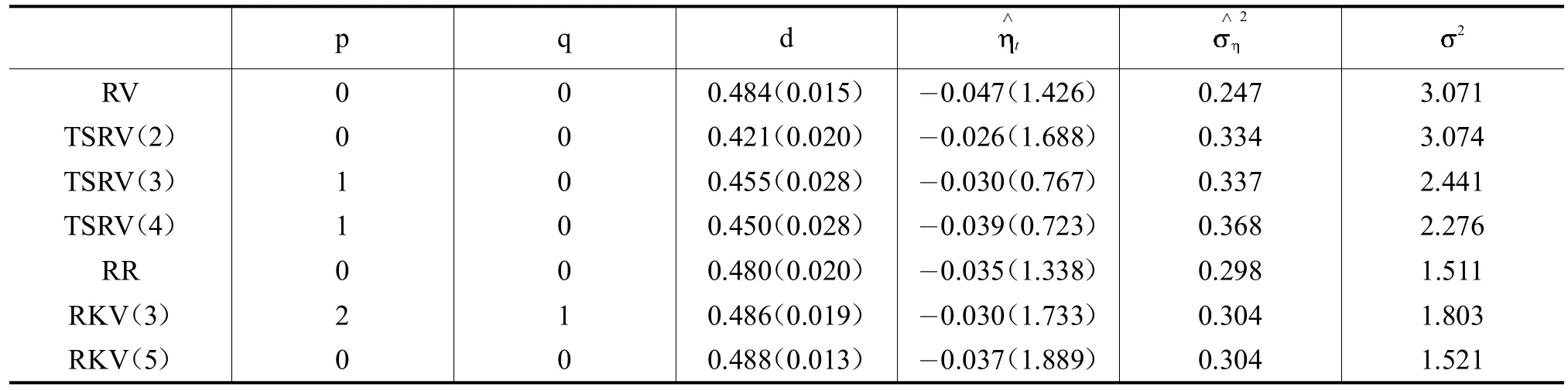
表2　ARFIMA模型阶数及参数估计结果

四、VaR建模与回测分析

（一）VaR建模

VaR俗称在险价值（Value at Risk，VaR），其定义为：

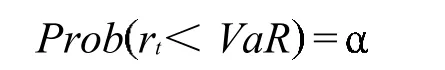
其中Prob为VaR的概率大于收益率rt的概率，rt为一定持有期t情况下的收益率，VaR即为显著性水平情形下的在险价值，此处取负。文献中持有期常取为1天，本文也采用持有期为1天，常用的显著性水平一般为5%，1%等。

空头头寸的

skst为相应偏学生分布的左尾分位数，skst1为右尾分位数。

（二）LR回测检验分析

一般情况下，基于不同波动率度量的VaR模型将有不同的VaR预测值，我们需要对VaR预测模型的有效性进行回测检验分析。目前最常用回测检验方法是Kuipec和Christoffersen提出的似然比LR检验法。[10-11]其构造似然比LR检验统计量，原假设为VaR模型是正确的，因此P值越大表明这个模型的预测精度越高。表3给出了5种显著性水平下各模型多头和空头LR检验的P值。表3中，加星号“*”表示在该显著水平下，该波动率度量最为准确。

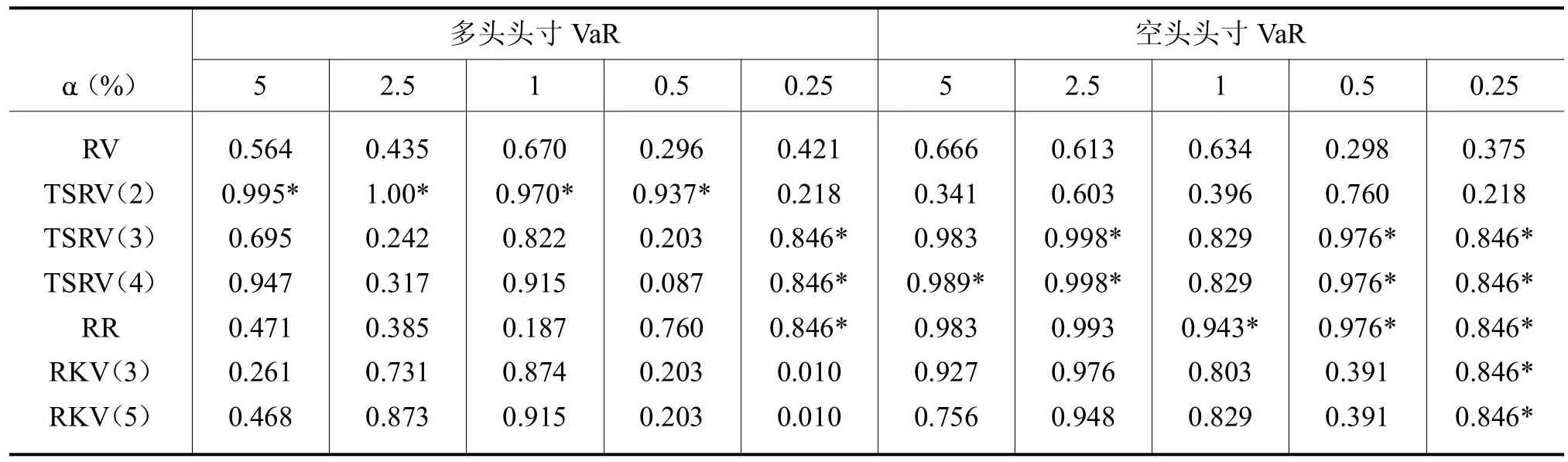
表3　各波动率LR模型检验结果

从表3的结果来看，基本可以得出如下结论：

1.总体来看，空头头寸的VaR度量和预测，要比多头头寸VaR度量预测要准确。在相同显著水平，空头头寸共有22组P值大于多头头寸，小于多头头寸共有9组，其中P值相等的组共有4组，整体上，空头表现优于多头头寸。

2.在多头头寸下，TSRV（2）表现最好，在空头头寸下，TSRV（4）表现最好。在多头情形下，5个显著水平中有4个显著水平下，TSRV（2）达到最优；在空头头寸下，也同样在4个显著水平下，TSRV（4）达到最优。

3.从多头头寸和空头头寸两方面同时来看，RV波动率度量预测较差，TSRV（4）最为稳健，为度量波动率的最优选择。如果以P值大于80%为限，认为大于80%表示模型准确，在10组显著性水平结果中，RV、TSRV（2）、TSRV（3）、TSRV（4）、RR、RKV（3）和RKV（5）依次有0、4、7、8、6、5和5。可以得出，在这几种波动率模型中，RV最差，TSRV（4）模型最好。这也表明数据中微观噪音必须给予充分考虑，TSRV这类能够处理微观噪音的波动率，优于通常的RV度量。

4.利用ARFIMA模型为TSRV（4）波动率进行动态建模，偏学生分布刻画收益率，建立VaR预测模型，具有可靠的稳定性和优良性，可以为实际VaR风险度量提供重要的借鉴。

五、结语

本文利用上证综合指数2004年1月2日至2012年7月26日的高频数据，基于各种波动率对数序列，构建ARFIMA模型，利用偏学生分布SKST刻画其日收益率序列，计算了两种头寸的VaR值。并利用LR检验方法进行回测检验，对上证综合指数进行实证分析，得出一些有意义的结论。

1.上证综合指数日收益率具有鲜明有偏性和尖峰厚尾性，收益率序列不具有长期记忆性，但波动率序列都具有鲜明长期记忆性，且对数变换后的波动率序列近似服从正态分布，提高了统计效率。

2.上证指数收益率的有偏性，影响了VaR预测效果，空头头寸的效果优于多头头寸，在多头头寸下，TSRV（2）最优，在空头头寸下，TSRV（4）最优。

3.从预测的精度来看，TSRV（4）模型的预测最为准确，也最为可靠。在微观噪音的影响下，不能处理微观噪音的RV模型预测精度较差，相对来说，TSRV、RR和RKV预测效果更好，且TSRV（4）最好。

4.基于TSRV（4）波动率度量构建的ARFIMA模型，结合偏学生分布刻画收益率，建立的VaR度量和预测模型，具有可靠稳定性和优良预测能力，可以为实际VaR风险管理提供模型方法参考。

这些发现意味着，合理利用能够处理微观噪音的波动率度量，并将这些度量方法用于VaR度量和预测，将大大提高风险管理水平，提高金融资产VaR预测精度。本文研究方法对金融资产风险管理理论和实践，也具有一定参考借鉴意义。

[1]Andersen T G，Bollerslev T.Answering the Skeptics：Yes，Standard Volatility Models Do Provide Accurate Forecasts[J].International Economic Review，1998，39：885-905.

[2]Zhang L，Mykland P A，Ait-Sahalia Y.A Tale of Two Time Scales：Determining Integrated Volatility With Noisy High-Frequency Data[J].Journal of the American Statistical Association，2005，100：1394–1411.

[3]Barndorff-Nielsen OE，Hansen P R，Lunde A，Shephard N.Designing Realised Kernels to Measure the Ex-Post Variationof Equity Prices in the Presence of Noise[J].Econometrica，2008，76：1481-1536.

[4]Parkinson M.The extreme value method for estimating the variance of the rate of return[J].Journal of Business，1980，53：61-65.

[5]Chou R Y.Forecasting financial volatilities with extreme values：the conditional autoregressive range（CARR）model[J].Journal of Money Credit and Banking，2005：561-582.

[6]邵锡栋，殷炼乾.基于实现极差和实现波动率的中国金融市场风险测度研究[J].金融研究，2008，（6）：109-121.

[7]韩清，刘永刚.已实现波动率估计中不同降噪方法的比较分析及实证[J].数量经济与研究，2009，（8）：148-160.

[8]Brownless C T，Gallo G M.Comparison of volatility measures：A risk management perspective[J].Journal of Financial Econometrics，2010，8（1）：29-56.

[9]Andersen T G，Bollerslev T，Diebold F X，Labys P.Modeling and Forecasting Realized Volatility[J].Econometrica，2003，71：529-626.

[10]Kupiec P.Techniques for verifying the accuracy of risk measurement models[J].Journal of Derivatives，1995，3（2）：73-84.

[11]Christoffersen F.Elements of Financial Risk Management[M].McGill University and CIRANO，2002.

[责任编辑：辛晓莉]

F222

A

1674-3288（2014）04-0046-05

2014-06-25

国家自然科学基金项目“含微观噪音半鞅的二维尺度幂变差及其应用”（11226201）；教育部人文社会科学研究项目“含微观噪音金融高频数据的统计分析及其在VaR度量中的应用”（12YJCZH128）；江苏省自然科学基金项目“含微观噪音过程的两维度幂变差理论及其金融高频数据应用”（BK20131340）；2012年江苏省“青蓝工程”学术骨干；江苏省高校优势学科建设工程资助项目（应用经济学）；江苏省高校重点实验室金融工程实验室资助项目

刘广应（1980-），男，安徽合肥人，博士，南京审计学院金融数学与金融工程系副教授，研究方向：金融数学、应用统计、金融风险管理；马丽娟（1992-），女，江苏南京人，南京审计学院数学与应用专业（数理金融方向）学生。