基于非线性混合模型对股市价格预测兼对比分析

赵 庆

（1.东北财经大学 金融学院，辽宁 大连 116025；2.辽宁对外经贸学院 财政金融系，辽宁 大连 116052）

基于非线性混合模型对股市价格预测兼对比分析

赵 庆1，2

（1.东北财经大学 金融学院，辽宁 大连 116025；2.辽宁对外经贸学院 财政金融系，辽宁 大连 116052）

为更精确地预测股市价格未来走势，提出一种新的预测模型：首先采用HP滤波将时间序列分解为趋势序列和周期序列，然后根据序列建模要求，对趋势序列采用自回归模型（AR）进行拟合和预测，对周期序列采用GARCH模型族进行拟合和预测，最后将趋势序列预测值和周期序列预测值相加，与原序列进行比较，进而选择模型精确度较高的模型。通过实证对比其他模型分析，该模型预测效果较好，可以为金融预测提供帮助。

沪深300指数；HP滤波；AR模型；GARCH模型

一、引言

混合模型是在多种模型的基础上提出新型模型的一种方法，相比单一模型具有较高的预测精度。关于HP滤波的使用领域，主要用于宏观经济分析，鲜见于资本市场。韩蓓（2009）使用HP滤波法对1982—2007年北京市潜在经济增长率进行测算，对未来潜在经济增长率的水平及适度增长区间作初步预测。[1]焦继文、陈文天（2012）利用HP滤波法对1998年3月至2011年11月我国房地产开发综合景气指数进行分析，分解出房地产业的循环因素，并在此基础上表征房地产周期与房地产政策的关联。[2]彭兆祺、孙超（2011）以GDP这一单变量作为分析对象，采用HP滤波方法，对我国经济的长期均衡增长或潜在增速进行考察。[3]吕超、王清川（2012）采用HP滤波法对我国的证券市场波动的周期性特征及中美两国证券市场波动的协同性进行了研究，得出了我国证券市场波动幅度严重偏大的结论。[4]W.Razzak（1997）基于HP滤波方法对新西兰1983年第1季度至1995年第3季度实际国民生产总值进行了分析，估计了新西兰实际产出缺口。[5]

自回归模型在宏观经济管理、数学、电信技术、金融、地质学、计算机软件及计算机应用、化学、自动化技术、物理学和建筑学等众多学科中有着广泛的应用。在这里，我们仅对基于AR模型预测功能的具有代表性的文献进行简单叙述。金瑶、蔡之华（2013）使用AR模型及Kalman滤波对股票价格进行了预测。[6]高宁、崔希民和高彩云（2013）基于灰色系统和AR模型对建筑物沉降变形进行了预测。[7]黄鹂（2013）基于AR模型和ARCH模型对我国房屋销售价格指数进行了预测。[8]

GARCH模型自从诞生之日起便广泛应用于各个领域，尤其是在金融时间序列分析中。黄海南、钟伟（2007）运用GARCH族模型对上证指数收益率进行了全面的估计及样本外预测，发现无论是样本内还是样本外，GARCH类模型都能够较好地预测上证指数的收益波动率。[9]张跃军、范英、魏一鸣（2007）基于GED—GARCH模型的中国原油价格波动特征研究，发现GARCH模型能够更好地描述中国原油价格的波动特征，并且具有较好的预测能力。[10]Dueker（1997）运用Markov—GARCH转换模型模拟和预测了股指的可变性，发现区制转换模型要比单一区制模型具有更优的预测性。[11]赵庆、王志强（2014）运用混合模型对上海黄金交易所现货黄金Au99.99日收盘价进行了预测。[12]

本文试图在前人工作的基础上，提出一种新的预测模型。利用HP滤波—AR模型—GARCH族模型对股指期货的标的物沪深300的收盘价进行实证建模分析，选出最优的模型来预测沪深300，同时与其他文献所选模型进行对比分析。

二、实证分析

（一）数据选取

本文选取中国股指期货合约标的沪深300指数为研究对象，选取2011年8月1日至2013年9月17日的收盘价，单位：元。剔除节假日数据共517条数据。选取前466个数据进行模型的建立，然后对样本外的51个数据进行样本外预测。数据来源于Wind资讯金融终端。

（二）HP滤波对原序列的分解

（三）对趋势序列拟合和预测

1.单位根检验

对于趋势序列T，使用自回归模型进行拟合和预测，首先对趋势序列T进行单位根检验，结果：ADF=概率值（P值）=0.0403，小于5%显著水平临界值，所以趋势要素序列T在5%显著水平下是平稳序列。

2．趋势序列相关检验及建立模型

通过对趋势序列T进行自相关检验，可发现自相关系数是拖尾的，偏自相关系数在4阶结尾。同时根据AIC、SC最小准则确定模型的阶数，以前466个数据作为建模数据，经过多次拟合对趋势序列T建立AR（4）模型，拟合系数R2=0.999998，拟合效果非常好，模型回归参数见表1。

表1 趋势序列T自回归模型参数

在AR（4）模型的基础上采用静态预测法对样本外的51个数据进行预测，预测效果如图1所示。

从图1，可以看出趋势序列T和趋势预测序列TF近乎完全重合，预测效果很好。由此可以得到回归模型未预测的带有周期的随机波动序列然后利用GARCH族模型对C0进行拟合和预测。

（四）利用GARCH族模型对带有周期随机波动序列C0拟合和预测

1.周期随机波动序列C0的正态分布检验

由于采用AR（4）模型进行预测，因此预测序列TF缺失5个数据，故此C0为512个数据。C0的正态分布检验采用 J—B统计量方法。检验结果：峰度=2.873386，偏度=40.195935，J—B统计量值=3.617992。可以发现，周期随机波动序列C0不但不服从正态分布，而且具有过度峰度、厚尾和左偏的特征。

2．周期随机波动序列C0的ADF检验

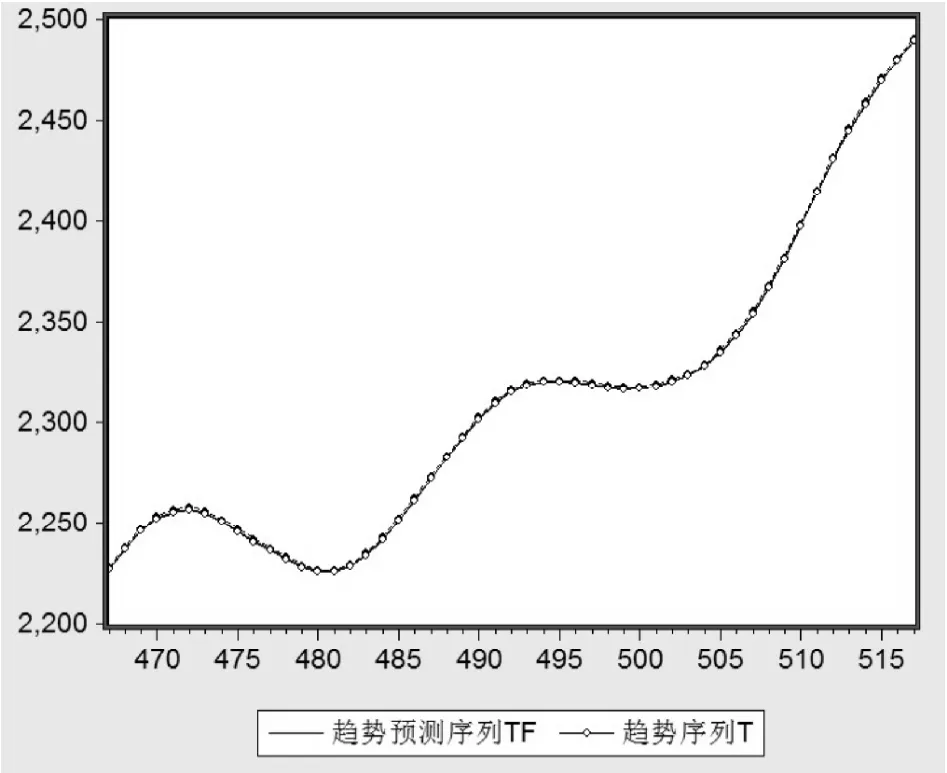
图1 趋势序列样本外预测

对周期随机波动序列C0进行单位根检验结果：ADF=13.79752，概率值（P值）=0.0000，小于1%显著水平临界值，所以周期随机波动序列C0在1%显著水平下是平稳序列。

3．周期随机波动序列C0的序列相关检验

通过对周期随机波动序列C0的序列相关检验，可发现周期随机波动序列C0存在多阶自相关和偏自相关。

综上所述，周期随机波动序列C0为平稳序列但是存在自相关，所以回归方程为自回归移动平均模型（ARMA模型）。因此根据AIC、SC最小化准则进行多次尝试来确定模型的阶数，最后确定为ARMA（5，6），由于常数项C不显著（t值为 0.173278），故剔除常数项，重修估计其他AR、MA项结果均显著，参数估计如表2所示。

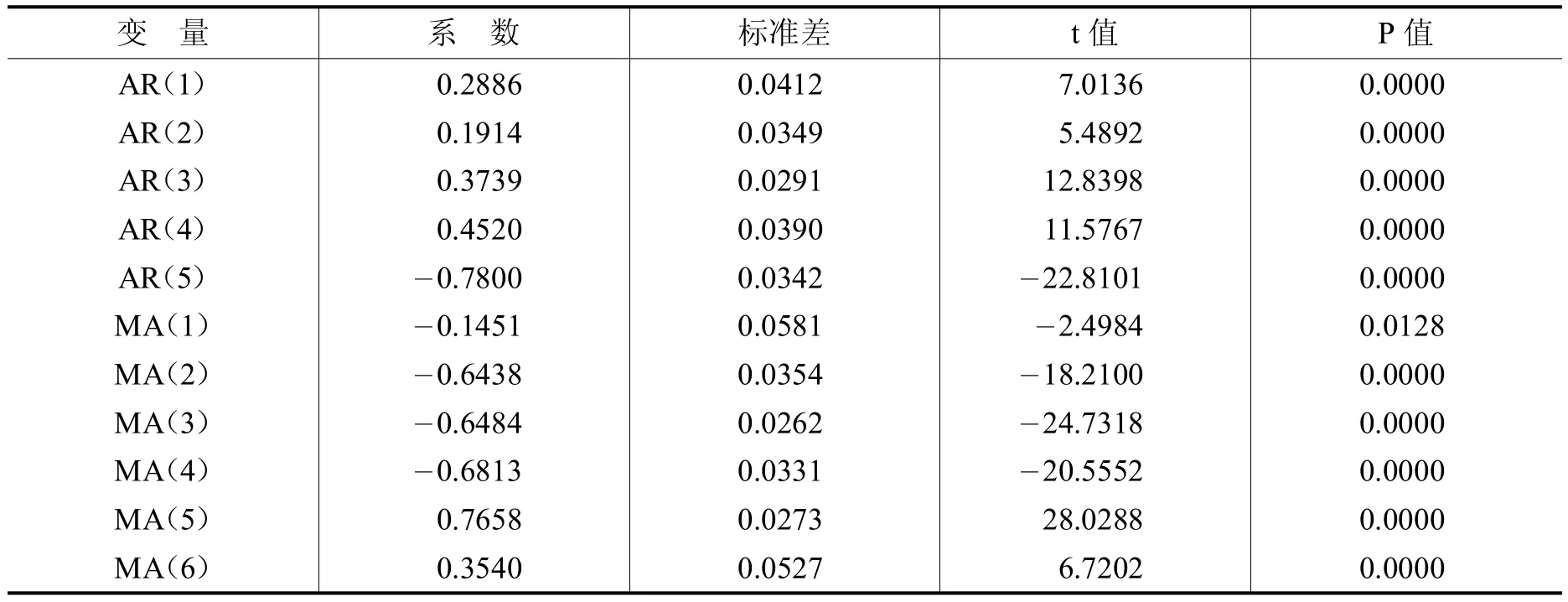
表2 周期随机波动序列C0自回归移动平均模型回归参数

4．周期随机波动序列C0的ARCH效应检验

基于对周期随机波动序列C0的回归方程ARMA（5，6）的残差进行ARCH—LM检验，以验证时间序列是否具有ARCH效应。在x2检验的阶数q=4时，得到以下结果。

表3 周期随机波动序列C0的ARCH-LM检验结果

由表3可知，T×R2统计量的伴随概率为0.0023＜0.05，说明残差序列存在ARCH（4）效应，因此，模型应采用GARCH（p，q）模型。

5．GARCH（p，q）模型的遴选

对周期随机波动序列C0分别拟合GARCH、EGARCH、TARCH、EGARCH—M、TARCH—M、CARCH模型，来选择最佳的表达模型。对周期随机波动序列C0的ARMA（5，6）模型残差检验采用J—B统计量方法，检验结果显示：峰度=3.077225，偏度=0.080509，J—B统计量值=0.605922，可以发现，周期随机波动序列C0不服从正态分布，因此，在用GARCH族模型进行拟合时，选择残差服从学生t分布。针对周期随机波动序列C0，由于采用AR（4）模型预测趋势序列T，因此其预测序列TF缺失5个数据，共512个数据，利用前456个数据为模型拟合，而将后51个数据作为预测值，这样方便与趋势要素预测值TF相结合，作为模型预测性能评价参照数据。另外，在对各个模型阶数进行确定时同样采用AIC、SC最小化准则。最后，从中遴选出6个拟合效果较好的模型：GARCH（1，3）、EGARCH（1，1）、TARCH（1，1）、EGARCH—M（2，2）、TARCH—M（2，1）、CARCH（1，1），其中EGARCH—M（2，2）、TARCH—M（2，1）均值项（mean）选择加入条件为标准差，模型参数如表4所示。

由表4可知，GARCH族模型中所对应的AIC、SC相差并不大；从模型的显著性角度看，EGARCH（2，1）、TARCH（1，1）和EGARCH—M（2，2）中各系数非常显著地不为零，模型较优。在TARCH模型中，杠杆效应项的系数=0.019285，说明周期随机波动序列C0具有“杠杆效应”：“利空消息”比等能量的“利好消息”产生更大的波动，但其z统计量为 0.148302，不显著，说明了周期随机波动序列C0具有一定程度的弱杠杆效应，这个

具有弱杠杆效应的结果在EGARCH模型中同样得到印证，非对称项的估计值为 0.083002，说明具有“杠杆效应”，同样其z统计量为 1.291385，不显著。在EGARCH—M（2，2）、TARCH—M（2，1）模型中，条件标准差系数估计值均为正数，说明对于周期随机波动序列C0而言，收益与风险存在正相关关系，但是其z统计量不显著，说明这种关系并不显著。

表4 周期随机波动序列G0的GARCH族模型参数估计与检验结果

（五）预测效果分析

将利用自回归模型对趋势要素T预测的元素序列TF与利用GARCH模型族对周期随机波动序列C0的预测序列C0F进行重组，即NF=TF+C0F作为沪深300指数收盘价的预测序列，共计51个评价数值，误差率采用预测值NF减去原序列N的绝对值除以原序列N，平均误差率采用误差率自然平均数。预测结果如表5所示。

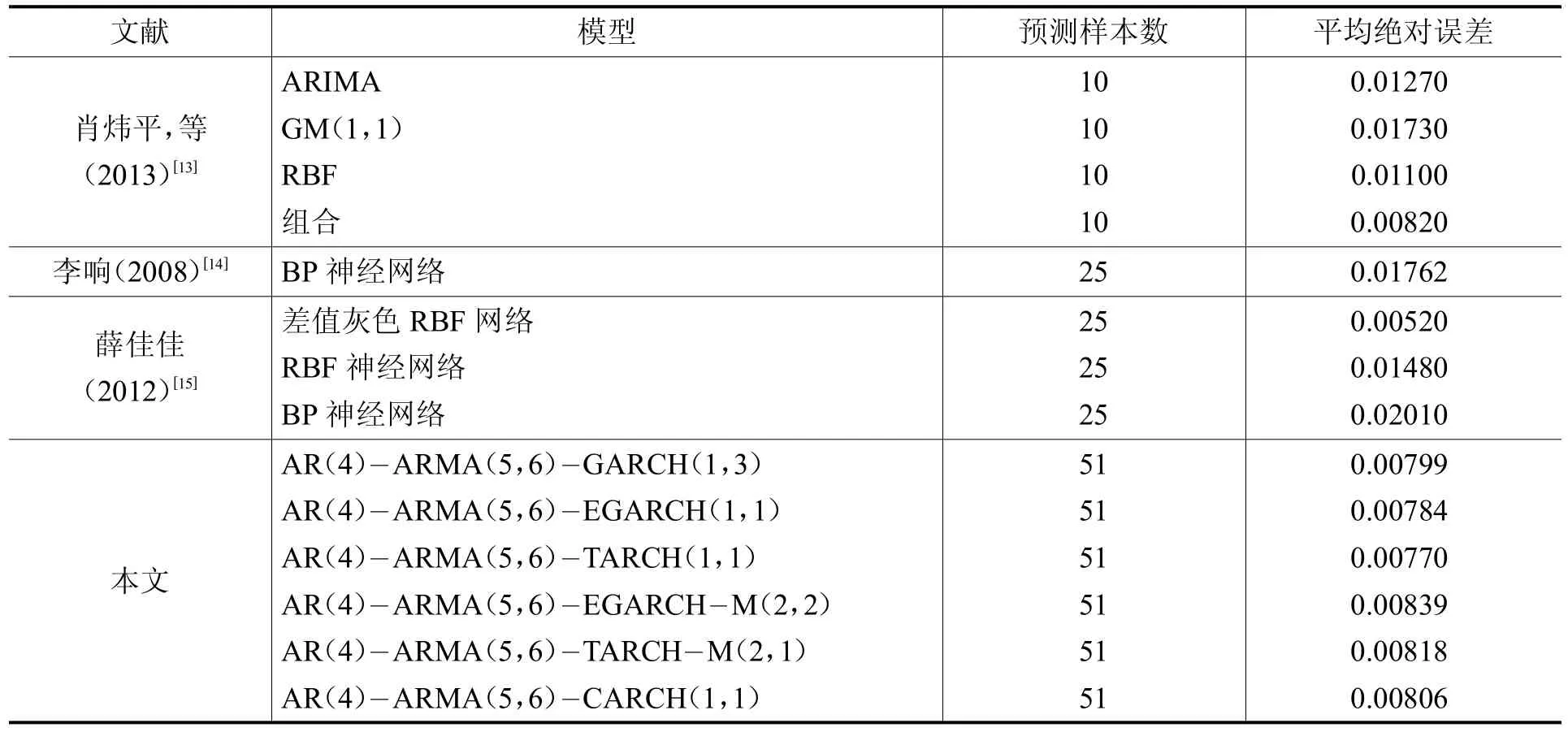
表5 预测结果比较分析

由表5可以看出，在采用HP滤波—ARMA—GARCH族模型对沪深300指数的收盘价预测时，所有模型的平均误差率均低于1%，整体预测效果很好。其中HP滤波—ARMA—TARCH（1，1）准确率达到99.23%，在所有遴选模型中准确率最高。并且本文所选模型预测精度整体而言相比其他三篇文献所选模型要高，仅比薛佳佳（2012）所选差值灰色RBF网络模型预测精度略低，但是预测范围要比其大得多。显然，本文模型对于预测具有直接的借鉴意义。

三、总结

由于长期以来，预测股市价格变动，预测资本市场的发展都被认为是富有挑战性的工作，在学术界对于股票市场大多数认为存在“布朗运动”学说和“不可知论”。本文对股票价格预测进行了一次新的尝试，提出了一种新的预测方法和思路，采用HP滤波—AR—GARCH族模型对沪深300指数收盘价进行了有效拟合和预测，首先通过HP滤波法将沪深300指数收盘价进行分解，分解为趋势要素和周期要素，然后分别对不同性质的要素进行预测，然后合并，通过合并后的预测值与实际值相比较，结果表明预测效果很好，并且同时与所选模型进行对比，无论从预测精度和预测范围而言，都证明该模型对于实践应用具有指导意义。

[1]韩蓓.北京市潜在经济增长率测算与HP滤波平滑参数探讨[J].云南财经大学学报，2009，11（2）：139-146.

[2]焦继文，陈文天.基于HP滤波法的我国房地产周期与房地产政策关联性研究[J].建筑经济，2012，29（8）：79-83.

[3]彭兆祺，孙超.基于HP滤波分析方法的我国经济增长研究[J].山西财经大学学报，2011，33（4）：15-17.

[4]吕超，王清川.基于HP滤波法的证券指数波动的协同性实证检验[J].统计与决策，2012，355（7）：111-113.

[5]W.RAZZAK.The Hodrick-Prescott technique：A smoother versus a filter An application to New Zealand GDP[J].Economics letters.1997，57（2）：163-168.

[6]金瑶，蔡之华.基于AR模型的Kalman滤波在股票价格预测中的应用[J].统计与决策，2013，378（6）：80-82.

[7]高宁，崔希民，高彩云.灰时序GM-AR模型在建筑物沉降变形预测中的应用[J].测绘科学，2013，37（1）：139-141.

[8]黄鹂.我国房屋销售价格指数AR模型的预测分析[J].统计与决策，2013，379（7）：75-78.

[9]黄海南，钟伟.GARCH类模型波动率预测评价[J].中国管理科学，2007，15（6）：13-19.

[10]张跃军，范英，魏一鸣.基于GED-GARCH模型的中国原油价格波动特征研究[J].数理统计与管理，2007，26（3）：398-406.

[11]DUKER M J.Markov switching in GARCH processes and mean-reverting stock volatility[J].Journal of Business，Economics and Statistics.1997，94（15）：26-34.

[12]赵庆，王志强.基于HP滤波-AR模型-GARCH族模型对黄金价格预测研究[J].黄金，2014，35（3）：4-8.

[13]肖炜平，刘新卫，张威.基于非负权重最优组合预测的股价预测研究[J].统计与决策，2013，390（18）：142-145.

[14]李响.基于BP神经网络的股价预测[J].大连海事大学学报，2008，34（6）：114-116.

[15]薛佳佳.基于差值灰色RBF网络模型股票指数预测[J].统计与决策，2012，370（20）：77-79.

[责任编辑：辛晓莉]

F830.91

A

1674-3288（2014）05-0046-06

2014-07-12

大连市社会科学研究基地2013年度开放课题（2013LBGMJD004）;辽宁对外经贸学院2013年度校级青年项目（2013XJLXQN005）

赵庆（1983-），男，辽宁大连人，东北财经大学金融学院博士研究生，辽宁对外经贸学院财政金融系讲师，研究方向：金融工程。