P2P网络合作节点信任机制的探索与研究＊

卫 娟，戴 冬

（河南机电高等专科学校 计算机科学与技术系，河南 新乡 453000）

近十年来，P2P技术的出现为解决大规模流媒体分发难题带来了新的契机，P2P网络不同于传统的网络架构，其充分利用了网络中Peer节点的缓存和带宽资源，让Peer节点也承担内容分发工作。在P2P网络中，Peer节点担任着两个角色，其既是资源的提供方，也是资源的享用方。系统的可用资源随着在线Peer节点数的增加而增长，服务能力也随之增长。在这种网络环境下服务商不需要为每个节点直接提供服务，其服务压力被减轻、运营成本也大大降低。然而，P2P系统中节点的信任问题一直都是系统稳定性的潜在隐患。针对这一问题，本文给出一种信任模型，能够有效地判断合作节点的信任程度。

1 信号博弈的概念

信号博弈是一类在两个博弈方之间的不完全信息动态博弈的总称，许多博弈都可以归结为该类型的博弈。这种博弈中的两个博弈方各自都只有一次行为，后行为的一方具有不完全信息，但他可以从先行为一方的行为中获得部分信息，因此先行为一方的行为对后行为一方来讲就好像是一种以某种方式反映其得益函数的信号，因此这种博弈被称为信号博弈。信号博弈是比较简单的动态贝叶斯博弈。

一般信号博弈中先行为一方为信号发出方，称后行为一方为信号接收方。如将信号博弈转换成完全但不完美的信息动态博弈。设有一个博弈O方先为发出方按一定概率从其类型空间中随机选择一个类型，并将该类型告诉发出方；然后是发出方在自己的行为空间中选择一个行为；最后是接收方根据发出方的行为选择自己的行为。如果我们用S表示信号发出方，用R表示信号接收方，用T＝｛t1，…，tI｝表示S的类型空间，用M＝｛m1，…，mJ｝表示S的行为空间，或称信号空间，用A＝｛a1，…，ak｝表示R的行为空间，用US，UR分别表示S和R的得益，并且设博弈方O为S选择类型的概率分布为｛p（t1），…，p（ti）｝。则一个信号博弈可表示为：

发送方（S）知道自己的类型ti，然后从可行的行为空间M＝｛m1，…，mJ｝中选择一个行动mj。

接收方（R）观测到mj，然后从可行的行为空间A＝｛a1，…，aK｝中选择一个行动aK，这里ak依赖于自身的类型ti。

双方的得益函数分别为uS（ti，mj，ak）和uR（ti，mj，ak）依赖于ti，mj，ak并且是共识。

2 选择任务合作节点

在P2P网络系统中，节点A需要寻求合作节点共同完成某一项任务。节点A与欲合作节点双方均以各自的利益最大化为目标。设申请合作的欲合作节点的信任值不尽相同，信任值是指提供的节点在任务完成之前不会随意中断服务的概率。节点A给予合作节点的统一服务价格为M，申请合作的欲合作节点根据其自身的实际情况（即信任值）及统一价格M，向节点A承诺一个违约保证金L。如果其不能完成节点A指派的任务，则向节点赔偿L，否则节点A向合作完成的合作节点支付服务费M。若节点A分配的任务顺利完成，则其获利为J，否则其遭受的损失为F。假定申请合作的欲合作节点信任节点A，其合作交易过程如图1所示：

图1 合作节点合作流程图

（1）节点A在系统中发布寻求合作信息，并给出合作价格m，并且提供决策所需的信息d，e，限定合作节点只能在任务执行前的一段时间内提出合作信息。

（2）符合条件并希望进行合作的欲合作节点根据其自身的信任值φ按下列函数U（φ）计算其违约保证金L＝U（φ），

（3）欲合作节点在系统中向节点A申请合作，同时在节点A指定的账户预存入违约保证金L。

（4）节点A根据欲合作节点提供的违约保证金L按下列方法判断其信任值φ的取值：若L＜L4，则φ∈（0，φ4）；若L＝L4，则φ∈［φ4，φ5］；若L4＜L＜L2，则φ＝φ1；若L≥L2，则φ∈［φ2，1）。

（5）节点φj根据申请合作的欲合作节点的由高到低依次选取一定量的节点作为任务合作节点。

（6）最后节点A与合作节点签订任务合同。

3 模型应用

假设节点A在Ti时段需要为节目a选取20个视频分发预约合作节点，如表1所示。

表1 交易相关参数

（1）节点A根据自身的运营成本以及预计的获利情况，制定出Ti时段网站所需合作统一价格M＝1，然后，在系统中发布需要在Ti时段选取50个合作节点的需求信息，并且为欲合作节点提供与交易相关的参数值，其中，合作价格M＝1、d＝0.2、e＝0.01、J＝8、F＝2。

（2）假设现有100个的欲合作节点符合条件，这些欲合作节点向节点A提出申请，并且根据自身服务信任值φj给出了相应的违约保证金L（该值可根据前面介绍的计算公式得出），表2给出100个欲合作节点给出的违约保证金额。

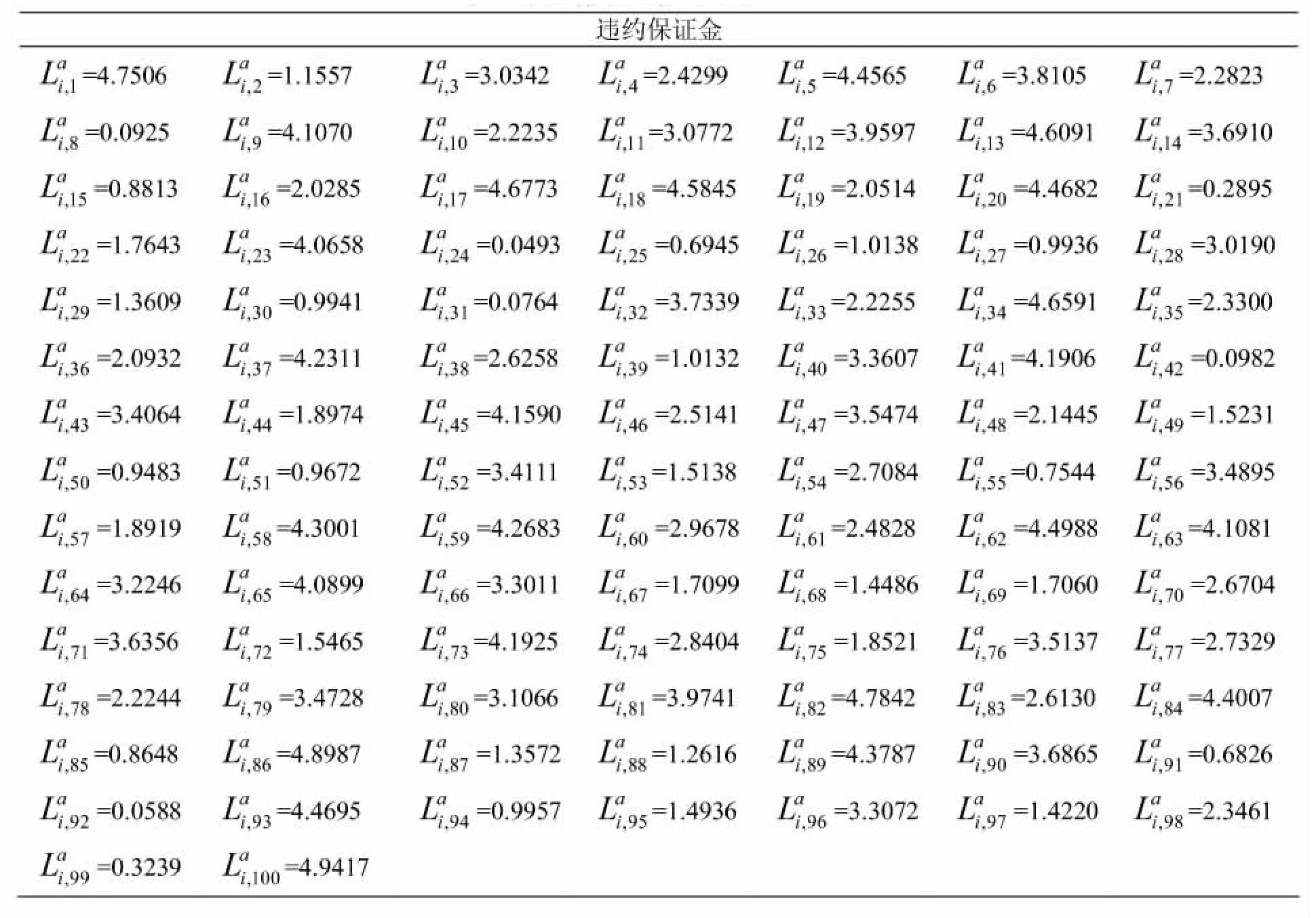
表2 欲合作节点给出的违约金

（3）节点A根据欲合作节点提供的违约保证金L按下列方法判断其信任值φj的取值，由（1）中给出的参数值M＝1、d＝0.2、e＝0.01、J＝8、F＝2可知以得出模型中参数值：φ2＝0.9088、φ4＝0.2000、φ5＝0.2548、L2＝4.9500、L4＝0.2500。若＜0.2500，则欲合作节点的信任值φj∈＝0.2500；若L＝0.2500，则欲合作节点的信任值；φ∈［0.2000，0.3548］若0.2500＜L＜4.9500，则若L≥L2，则φj∈［0.998，1］。

最终节点A确定的合作节点为：

其中，Xai，n代表第n个合作节点。

（责任编辑吕春红）

［1］ 田春岐，等.一种基于信誉和风险评价的分布式P2P信任模型 ［J］.电子与信息学报，2007，（07）.

［2］ 李勇军，等.对等网络信任机制研究［J］.计算机学报，2010，（03）.

［3］ 李明楚，等.基于反馈机制的网格动态授权新模型［J］.计算机学报，2009，（11）.

［4］ 张润莲，等.一种基于实体行为风险评估的信任模型［J］.计算机学报，2009，（04）.

［5］ 李小勇，桂小林.可信网络中基于多维决策属性的信任量化模型［J］.计算机学报，2009，（03）.

［6］ 田春岐，等.一种基于推荐证据的有效抗攻击P2P网络信任模型［J］.计算机学报，2008，（02）.

［7］ 李小勇，桂小林.大规模分布式环境下动态信任模型研究［J］.软件学报，2007，（06）.

［8］ Girvan M，Newman M E J.Community structure in social and biological networks［J］.Proceedings of the National Academy of Sciences of the United States of America，2002.

［9］ Clauset A，Newman M E J.Finding community structure in very large networks［J］.Physical Review，2004.