敞开式太阳能集热/再生器的理论模型及性能分析
彭冬根,张小松,郭兴国
(1.南昌大学 建筑工程学院,南昌 330031;2.东南大学 能源与环境学院,南京 210096)
敞开式太阳能集热/再生器的理论模型及性能分析
彭冬根1,张小松2,郭兴国1
(1.南昌大学 建筑工程学院,南昌 330031;2.东南大学 能源与环境学院,南京 210096)
对敞开式太阳能集热再生器建立理论解析模型,理论求解发现溶液在常温下再生时存在一个最佳单位面积流量使单位面积蒸发率最大。溶液入口温度和室外风速是决定最佳流量值的2个最重要参数,溶液浓度和太阳辐射强度对最大蒸发率影响最明显。当溶液出口温度低于入口温度时,最佳流量不存在,溶液流量越大再生效果越好。当室外风速为2 m/s时,溶液再生蒸发率最大。文章全面揭示了影响敞开式集热/再生器性能的各项因素。
集热/再生;最佳单位面积流量;再生蒸发率
太阳能溶液除湿蒸发冷却空调系统[1-4]是一种利用太阳能低温热源驱动、以自然工质(空气或水)为制冷剂的空调系统。在利用太阳能低温(60~80℃)热源驱动的溶液除湿空调系统中,太阳能集热和溶液再生装置是其中2个重要部件,是太阳能溶液除湿蒸发冷却空调技术进入市场化应用中必须要研究的。学者们将太阳能集热和溶液再生相结合构建太阳能溶液集热/再生装置,文献[5-6]发现太阳能溶液集热/再生装置具有较高的再生效率。太阳能集热再生装置分为自然和强迫对流2种,尽管文献[7]显示强迫对流要优于自然对流,但强迫对流装置系统复杂、不如自然对流能更好实现建筑一体化设计。国外学者最早是采用自然对流方式对溶液进行集热/再生,并且是直接采用斜屋顶对溶液进行集热/再生[8]。自然对流太阳能集热/再生装置依据它与室外环境的接触程度,分为敞开式、部分敞开式及带玻璃盖板封闭式。1979年Collier[9]设计了一种敞开式自然对流集热/再生模式,发展了自然对流条件下水分蒸发率的解析求解方法。Nelson等[10-11]设计了一种带玻璃盖板的自然对流集热/再生器,再生用空气在浮升力作用下流过盖板和吸热板之间的通道和溶液进行传热传质。左远志等提出一个两级带盖板的太阳能平板集热再生装置[12]及太阳能槽式与平板式联合集热溶液双效再生装置[13]。Gandhidasan等[14-15]提出一种部分敞开式集热/再生器,该集热/再生装置分为带玻璃盖板段和敞开段,溶液在带盖板段仅被加热升温到再生所需温度,在敞开段内与大气直接接触进行传热、传质实现再生功能。高洪涛等[16]研究集热板形状对集热再生器性能影响,发现开有宽度为1 mm的纵向沟槽换热板的性能较好。文章理论推导出敞开式太阳能集热/再生器的蒸发率及溶液温度沿着集热板长度分布的解析模型,并分析该装置在最佳单位流量下的理论性能。
1 敞开式太阳能集热再生器的理论模型
敞开式自然对流太阳能溶液集热/再生过程中,溶液吸收太阳辐射能温度升高,通过直接与室外空气进行传热、传质,溶液中水分蒸发出去,从而使溶液浓度得到提纯再生。为了对该溶液再生器进行性能研究,必须对它建立数学模型。为了简化计算,提出物理模型假设为:
1)由于集热板背部有厚的保温层,可以忽略集热板背部散热,只考虑溶液向外界环境散热量;
2)再生溶液的流动和传热在流动方向上呈一维变化;
3)忽略溶液在流动方向上的导热和质量扩散,认为溶液和室外空气间传热、传质仅由对流引起;
4)由于液膜传热系数远大于空气对流传热系数,忽略液膜对传热和传质的阻力影响;
5)由于再生蒸发率远小于溶液流量,因此忽略溶液质量流量的变化;
6)室外环境为稳定状态。
根据以上假设,选取一微元体对它进行传热、传质进行分析(如图1所示),并得到溶液自然对流再生的数值计算模型:

式中:Ic为太阳辐射强度,k W/m2;α为吸收率;UL为散热系数,k W/(m2·K);Ts为溶液温度,℃;T0为环境温度,℃;ms,in为溶液入口质量流量,kg/s;mev为水蒸气蒸发率,kg/s;Cps为溶液比热容,kJ/(kg·K);hfg为水蒸汽的蒸发潜热,kJ/kg。

图1 自然对流集热/再生传热、传质微元体

式中:hm为传质系数,kg/(m2·s);YeL为溶液平衡含湿量,kg/kg或g/kg;Y0为环境空气含湿量,kg/kg或g/kg;ξ为溶液浓度;msalt为溶液中盐分质量流量,kg/s。
另外需构造溶液平衡含湿量YeL=f(Ts,ξ)模型,平衡含湿量YeL和溶液温度T、浓度ξ之间的数学关联式是非常复杂的,并且是非线形的,但是为了实现自然对流集热/再生过程的解析化,必须选择一个简化计算方程。当溶液温度和浓度在较小范围变化时,平衡含湿量可以通过下式计算得到:


为了分析溶液流量变化对蒸发率的影响,利用式(9)求解单位面积蒸发率(mev/x)对单位面积溶液流量(ms,in/x)的导数,并取为零值,见式(12)。

对式(12)进行迭代,可求出当mev/x为最大值时,单位面积流量(ms,in/x)值为最佳单位流量。
对于现如今医院的会计科目在改革时,设置专门的成本类科目尤为重要。设置成本类科目的过程中应该注意需保证医院的成本费用能够得到统一的管理,这样就能够使成本使用状况更加的清晰和具体,还能强化成本的可比性,其对于医院的会计管理工作效率提升具有一定的价值。对于医院的会计核算方式,进行必要的改革需要对于药品的销差价科目进行取缔,通过各种方法来增加医院的收入,比如增设药事费用等方案。这能在一定程度上是医院的收入状况得到明显的改善,可在一定程度上来保证医院的收入。还需要对于医院的会计核算内容进行明确,将会计管理中的医疗和药品等相关信息进行规范化的处理。
式(1)~(12)为溶液和空气间存在自然对流时的求解模型,它的存在条件为Ts>T0。反之当Ts≤T0时,溶液和空气间不会发生自然对流热、质传递,只存在热质扩散,但是其扩散系数非常小可以忽略。在该种状态下溶液吸收太阳辐射能温度升高,其传热模型可修改为

在求解溶液自然对流再生模型前,必须先选取散热系数UL、溶液和空气间传质系数hm的关联式。溶液向室外环境散热系数UL(式16)由对流散热系数hc和辐射散热系数hr2部分组成,辐射散热系数计算式见式(17),其中牵涉到有效天空温度Tsky的计算式,见式(18)。

溶液和环境空气间的对流传热、传质系数的计算方法视流动过程不同分为无风和有风2种。平板无风自然对流平均传热、传质系数计算关联式见式(19)和(20)。外掠平板有风强迫对流平均传热、传质系数计算关联式见式(21)和(22)。


式中,Nu为努塞尔数;Pr为普朗特数;Re为雷诺数;Sc为施密特数;Sh为舍伍德数;Gr为格拉晓夫数。
当Gr/≥0.1时,自然对流对溶液再生的影响不能忽略;反之则可只计算强迫对流对溶液再生作用。当Gr/≥10时,强迫对流的影响相对自然对流可以忽略。
2 模型验证
文章提出一种计算溶液自然对流集热再生过程单位面积最佳流量和最大蒸发率的理论计算模型,为了验证模型的正确性,将文献[9]在“湿热”和“干热”2种不同室外环境下氯化锂溶液单位面积最大蒸发率和最佳流量的计算结果和采用本文模型计算结果并行比较。文献[9]提出的“湿热”和“干热”2种计算工况的原始参数见表1,模型计算中维持室外温湿度及太阳辐射强度不变,改变室外风速、溶液入口温度,2种工况各取相同溶液浓度。本文和文献[9]计算结果比较如图2所示。图中“湿热”和“干热”2种工况各取5组计算结果进行比较。图2(a)为最大蒸发率比较,显示干热工况的蒸发率要远高于湿热工况,说明室外环境湿度对溶液再生影响很大。图2(b)同样显示大部分干热工况的最佳流量要高于湿热工况,但有一组干热工况计算结果低于湿热工况是由于其溶液入口温度为30℃低于60℃以上湿热工况再生。

表1 2种比较工况原始计算参数范围

图2 自然对流集热/再生传热、传质微元体
3 结果与讨论
3.1 集热板长度方向溶液再生能力分析
为了解自然对流再生过程中,在集热板长度方向溶液再生能力变化,文中对热稀(Ts=70℃,ξ=0.3)和冷浓(Ts=30℃,ξ=0.4)2种不同入口状态的LiCl-H2O溶液[17]再生过程进行解析计算,集热板长3 m。室外环境为:T0=38℃,Y0=0.025 g/kg。在溶液流量ms=25 kg/h条件下,2种溶液再生过程的蒸发率和温度在集热板方向的分布比较见图3,其中蒸发率为从溶液入口到计算点的累计值,其导数值为集热板长度上单位面积蒸发率值。图3显示当溶液处于冷浓状态下,溶液入口0.3 m段内由于溶液温度低于环境温度,在无风状态下溶液和空气间无法产生对流传热、传质,蒸发率mev为 0;之后受太阳辐射影响溶液温度提升到室外之上,但由于溶液表面水蒸气分压力小于环境空气中水蒸气分压力致使在x=0.3~1.0 m段内蒸发率为负值,表明溶液吸收室外水蒸气;随着溶液温度进一步上升,溶液内水分逐步蒸发到室外环境,蒸发率在集热板长度方向线形增加。当溶液处于热稀状态时,水蒸发率从入口至出口基本维持一定比率线形递增,这是由于溶液温度和浓度在集热板上最大变化幅度在9%内,并且溶液温度和浓度呈逆向变化,因此溶液和空气间的传质势差在集热板上基本保持不变。比较冷浓和热稀2种溶液的蒸发率在集热板长度的变化率可知,溶液浓度越高,蒸发率在集热板长度方向增加越平缓,这是由于浓度越高溶液表面水蒸气压力越低。
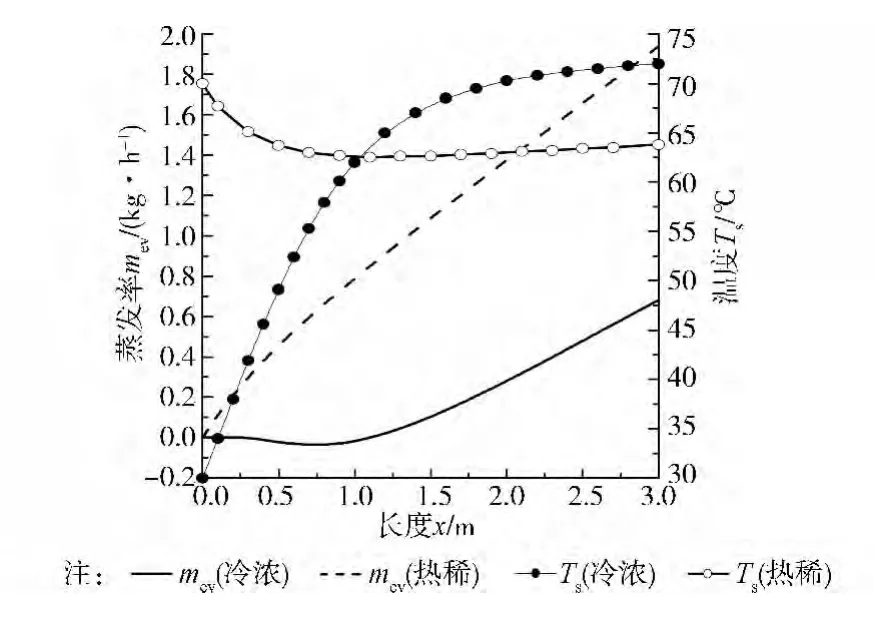
图3 集热板长度方向溶液再生能力分布
3.2 自然对流集热/再生的最佳单位流量分析
在模型分析中,指出太阳能自然对流集热/再生过程中存在一个最佳单位流量值,但是式(12)是通过迭代求解的,它是否有收敛解,这和溶液入口温度有直接关系。为分析溶液入口温度对最佳单位流量存在性的影响,选取40、70℃2种温度溶液分别在无风(V=0 m/s)和有风(V=2 m/s)情况的再生工况进行模拟比较,其他参数为:集热板长度l=10 m,太阳辐射强度Ic=800 W/m2,溶液入口浓度ξin=0.3,环境温度T0=33℃,含湿量Y0=20 g/kg。图4为无风和有风条件下,2种不同溶液入口温度的单位面积蒸发率mev/x、溶液出口温度Ts,out随单位面积溶液流量ms/x的变化。
图中显示无论是在无风还是有风情况下,单位面积流量ms/x从0.7 kg/(m2·h)增加到13.5 kg/(m2·h),溶液出口温度变化随溶液流量增加而递减,并且在溶液流量较少时递减速率更快。2者区别在于:当溶液入口温度Ts,in=40℃时,溶液出口温度位于55~80℃之间要高于入口温度,因此随溶液流量增加它需吸收更多显热而使温度递减;当溶液入口温度Ts,in=70℃时,除少数几个小流量工况下出口温度高于70℃,大多数流量工况下溶液出口温度要低于70℃,也就是说溶液进出口温度差为溶液再生提供显热,但是随溶液流量增加,溶液出口浓度下降致使水蒸发率上升,与之对应溶液出口温度也会相应下降,但渐趋平缓。比较2种温度溶液再生蒸发率mev随溶液流量变化可知,当再生过程溶液出口温度高于入口温度时,无论室外是否处于有风状态,确实存在一个最佳流量值,反之则不存在。比较无风和有风状态溶液再生性能可知,在有风状态下溶液出口温度要比无风状态低5℃左右,单位面积水蒸发率在ms/x<2.0 kg/(m2·h)时,有风状态蒸发率要稍低于无风状态;在mev/x≥2.0 kg/(m2·h)时,有风状态蒸发率要明显高于无风状态,并且溶液流量越大2者差值越大。从以上分析可知,只有当单位面积溶液流量超过一定值时,更高的传质系数(有风)才能提高溶液再生性能,这是因为室外风速不仅提高传质系数,同时提高溶液和空气的传热系数从而使溶液散热系数UL升高造成蒸发率下降。

图4 无风和有风状态下最佳流量分析
3.3 最佳流量工况性能分析
通过上节分析可知,溶液在常温再生(溶液出口温度高于入口温度)情况下存在一个最佳的溶液流量,也就是说在给定室外工况和溶液入口条件下通过改变溶液流量可以使溶液再生的蒸发率达到一个最大值。下文分析最佳流量及最大蒸发率随环境和溶液入口状态的变化趋势。其标准计算条件:集热板长度x=10 m,太阳辐射强度Ic=800 W/m2,室外风速V=0 m/s,环境温度T0=35℃,含湿量Y0=15 g/kg,溶液入口浓度ξin=0.35,入口温度Ts,in=33℃。分别改变环境温湿度及溶液入口参数、太阳辐射强度及室外风速,计算其在最佳流量条件下溶液再生特性。
3.3.1 室外温湿度变化对溶液再生作用
图5为环境含湿量Y0分别为12、20 g/kg时,环境温度改变对溶液再生性能影响。图中显示当环境温度从30℃增加到42℃,溶液最大水蒸发率 (mev/x)max呈线形上升,这是由于环境温度升高溶液和空气间的传热温差减少使散热损失降低。空气含湿量Y0为20 g/kg时单位面积最大蒸发率 (mev/x)max比为12 g/kg时要低0.03~0.04 kg/(m2·h),说明随环境湿度提高蒸发率明显降低,这是由于空气湿度升高后溶液和空气之间的传质势差减少,致使其蒸发率下降。另外,图中显示随环境温度升高,单位面积最佳流量(ms/x)opt呈波浪式增加,但还是维持在2.8~3.5 kg/(m2·h)之间变化,并且空气含湿量越高,最佳流量值越低。说明室外温度越高、含湿量越低(即相对湿度越小),则需要更多的溶液流量使再生效率最大。

图5 室外环境变化对溶液最佳再生作
3.3.2 溶液入口参数变化对溶液再生作用 图6显示当溶液入口浓度ξin为0.35和0.40时,溶液入口温度对溶液最佳再生工况的作用。图中显示当溶液入口温度从30℃增加到58℃,溶液最大水蒸发率(mev/x)max呈线形上升,这是由于溶液温度升高溶液表面水蒸气分压力增大使溶液和空气间的传质势差增大的缘故。在相同溶液温度条件下,溶液浓度ξin为0.40时蒸发率比浓度为0.35时降低0.08~0.10 kg/(m2·h),这是因为溶液浓度越高溶液表面水蒸气分压力越低所致。另外,图中表明当溶液入口温度小于45℃时,最佳溶液流量波动不大,处于3.0~3.5 kg/(m2·h)之间,但是随溶液入口温度进一步升高,最佳流量将快速增加,当溶液入口温度高于出口温度时,最佳流量将不存在。
3.3.3 太阳辐射强度及风速变化对溶液再生作用
图7为太阳辐射强度及室外风速改变对最佳流量和最大蒸发率的作用,图7(a)中太阳辐射Ic在500~1 100 W/m2间变化,图7(b)中室外风速V 在0~7 m/s间变化。图7(a)中显示随太阳辐射强度增加,最佳流量和最大蒸发率都呈线形上升,分别增加1.40、0.46 kg/(m2·h),增幅达60%和200%,最佳流量与太阳辐射强度呈正比变化说明越高的太阳辐射强度需要越多的溶液流量,蒸发率随太阳辐射强度升高而增加是不言而喻。图7(b)中显示最佳流量随室外风速增加,在3~6 kg/(m2·h)范围内波动变化,说明溶液最佳流量受风速影响巨大,室外风速越高则需更多溶液流量才能使其达到最大蒸发率工况;另外最大蒸发率在V=2 m/s时达到最大值,说明在小风速范围内,风速提高加强了溶液和空气间的传质效果使蒸发率上升,但是当风速超过一定值后,由于对流散热的增加反而使蒸发率呈下降趋势。因此,在溶液自然对流再生过程中并不是风速越大越好。

图6 溶液入口变化对溶液最佳再生作用

图7 太阳辐射及风速变化对溶液最佳再生作用
综合上述各种再生工况变化对溶液再生性能分析可知,溶液入口温度和室外风速是决定最佳流量值的2个最重要参数,其它参数变化对最佳流量影响可以忽略;在对最大再生蒸发率影响的各参数中,溶液浓度和太阳辐射强度作用效果最明显。
4 结 论
在对溶液平衡空气湿度YeL进行简单模型简化基础上,从自然对流溶液集热/再生数值模型推导出再生蒸发率和溶液温度在集热板长度分布的解析模型,并由此得出溶液自然对流集热/再生存在一个最佳单位流量,使得单位面积蒸发率最大。
对最佳单位流量分析发现,只有当溶液入口温度为常温时,最佳单位面积流量才存在;当溶液入口温度较高致使其出口温度低于入口温度时,单位面积蒸发率随流量增加而持续上升,不存在最佳单位流量值。
最佳流量工况性能分析可知,随室外温度升高、含湿量下降,最佳单位流量和最大蒸发率都增加;随溶液入口温度升高、浓度下降,最佳单位流量和最大蒸发率增加,当溶液入口温度大于50℃时,最佳单位流量快速升高,并且溶液浓度越低,最佳单位流量升高速度越大;随太阳辐射强度增加,最佳单位流量和最大蒸发率呈线形增加;室外风速增加会导致最佳单位流量上升,但是最大蒸发率随风速提高表现为先增后减变化,存在一个最大值。
[1]Lychnos G,Davies P A.Modelling and experimental verification of a solar-powered liquid desiccant cooling system for greenhouse food production in hot climates[J].Energy,2012,40(1):116-130.
[2]Audah N,Ghaddar N,Ghali K.Optimized solarpowered liquid desiccant system to supply building fresh water and cooling needs[J].Applied Energy,2011,88(11):3726-3736.
[3]Zeidan E B,Aly A A,Hamed A M.Modeling and simulation of solar-powered liquid desiccant regenerator for open absorption cooling cycle[J].Solar Energy,2011,85(11):2977-2986.
[4]Qi R H,Lu L,Yang H X.Investigation on airconditioning load profile and energy consumption of desiccant cooling system for commercial buildings in Hong Kong[J].Energy and Buildings,2012,49:509-518.
[5]Peng D G,Zhang X S.Modeling and simulation of solar collector/regenerator for liquid desiccant cooling systems[J].Energy,2011,36(5):2543-2550.
[6]Sultan G I,Hamed A M,Sultan A A.The effect of inlet parameters on the performance of packed towerregenerator[J].Renewable Energy,2002,26(2):271-283.
[7]Kabeel A E.Augmentation of the performance of solar regenerator of open absorption cooling system [J].Renewable Energy,2005,30(3):327-338.
[8]Kakabaev A,Khandurdyev A,Klyshchaeva O,et al.A large scale solar air conditioning pilot plant and its test results[J].International Chemical Engineering,1976,16:60-64.
[9]Collier R K.The analysis and simulation of an open cycle absorption refrigeration system [J]. Solar Energy,1979,23:357-366.
[10]Nelson D J,Wood B D.Evaporation rate model for a natural convection glazed collector/regenerator [J].Journal of Solar Energy Engineering,1990,112(1):51-57.
[11]Nelson D J,Wood B D.Two-dimensional,analysis and performance of a natural convection glazed collector/regenerator[J].Solar Engineering,1987,2:933-940.
[12]左远志,杨晓西,丁静.两级式太阳能平板集热型再生器及其稳态性能分析[J].化工进展,2009,28(2):222-225.
Zuo Y Z,Yang X X,Ding J.A two-stage collector/regenerator for solar liquid desiccant air conditioning system and its stable performance analysis [J].Chemical Industry and Engineering Progress,2009,28(2):222-225.
[13]左远志,杨晓西,丁静.新型太阳能槽式与平板式联合集热溶液双效再生系统[J].化工进展,2009,28(10):1734-1737.
Zuo Y Z,Yang X X,Ding J.A novel double-effect liquid desiccant dehumidifier with solar trough and flat plate dual collectors/regenerators [J]. Chemical Industry and Engineering Progress,2009,28(10):1734-1737.
[14]Gandhidasan P, Al-Farayedhi A A. Thermal performance analysis of a partly closed-open solar regenerator[J].Journal of Solar Energy Engineering,1995,117(2):151-153.
[15]Khalid C S,Gandhidasan P,Zubair S M.Exergy analysis of a liquid-desiccant-based,hybrid air-conditioning system[J].Energy,1998,23(1):51-59.
[16]高洪涛,富永康之,福永茂和,等.换热板形状对平板型吸收器传热性能的影响[J].太阳能学报,2005,26(2):294-298.
Gao H T,Fuyong K Z,Fuyong M H,et al.Effects of different geometric configurations of heat transfer plate on heat transfer characteristic of plate-type absorber[J].Acta Energiae Solaris Sinica,2005,26(2):294-298.
[17]Conde M R.Properties of aqueous solutions of lithium and calcium chlorides:formulations for use in air conditioning equipment design [J].International Journal of Thermal Sciences,2004,43(4):367-382.
(编辑 薛婧媛)
Modeling and Performance Analysis of Unglazed Solar Collector/Regenerator
Peng Donggen1,Zhang Xiaosong2,Guo Xingguo1
(1.School of Civil Engineering and Architecture,Nanchang University,Nanchang 330031,P.R.China;2.School of Energy and Environment,Southeast University,Nanjing 210096,P.R.China)
An analytical model of the unglazed solar collector/regenerator(C/R)was presented.There was an optimum flow rate per unit collector area at normal temperature which led to the maximum evaporation rate.The inlet temperature of absorbent solution and the wind velocity are key parameters to determine the optimum flow rate,in addition,the concentration of solution and solar radiation intensity have obvious effects on the maximum evaporation rate.When the outlet temperature of solution is higher than the inlet temperature,there is not an optimum flow rate,which reflects that the more the flow rate of solution is,the better regeneration efficiency is.With the 2m/s of wind speed,the evaporation rate reaches the peak.In this paper,kinds of factors influencing the performance of solar C/R were evaluated as well.
collector/regenerator;optimum flow rate per unit collector area;evaporation rate
TK511.3
A
1674-4764(2014)02-0068-07
10.11835/j.issn.1674-4764.2014.02.011
2012-10-26
国家自然科学基金项目(51266010);江西省科技支撑计划(20123BBG70195)
彭冬根(1975-),男,博士,副教授,主要从事太阳能制冷空调方面研究,(E-mail)ncu_hvac2013@163.com。

