超大跨径CFRP主缆悬索桥静力性能理论分析

王立彬，吴 勇

（南京林业大学 土木工程学院，南京 210037）

超大跨径CFRP主缆悬索桥静力性能理论分析

王立彬，吴 勇

（南京林业大学 土木工程学院，南京 210037）

首先推导了大跨悬索桥的无量纲形式平衡方程和协调方程得到索力和位移控制方程，然后推导了索力方程中的特征参数λ2的表达式，分析了参数λ2和载荷比P对索力和位移增量的影响。在此基础上，以3 000 m跨度悬索桥为算例，分析了在正反对称载荷工况下考虑和不考虑拉索弹性伸长情况下的悬索索力和位移增量的特征，最后对比钢索，分析了悬索桥跨度对CFRP缆索内力、位移控制方程参数的影响，以及参数变化对缆索体系悬索桥静力行为的影响，阐述了大跨CFRP悬索桥静力行为的本质特征，从理论上证明了CFRP悬索体系的优势和特点。

悬索桥；CFRP索；钢索；静力性能

现代悬索桥主缆一般都采用钢索，而缆索体系的缆索材料用量随跨度的平方增长。如果采用传统的钢索，主缆的自重将特别可观，其自重应力将消耗掉容许应力的相当大部分，承载效率会非常低［1］。另外，锈蚀也是钢索耐久性面临的严峻问题之一。正是由于钢索的这些缺陷限制了现代悬索桥向超大跨径的发展。碳纤维复合材料（简称CFRP）具有轻质高强、耐腐蚀、耐疲劳等特点。这些性能特点说明CFRP很有可能代替钢材成为主缆用材，很多学者对用CFRP的桥用性能进行了研究。

Meier［2］提出了CFRP用于桥梁缆索体系的思想并在Stork桥上首次应用CFRP索，对该桥长期的跟踪监测表明，CFRP索的测试结果超过了预期效果。吕志涛等［3］在江苏大学建设了首座CFRP索斜拉桥。在理论研究方面，Wang等［4－5］研究了CFRP、BFRP、B／SFRP等6种不同组成成分的FRP力学性能和疲劳性能，从拉索强度和等效刚度的基础上，评估了各种CFRP拉索的安全因子，分析了这6种千米级CFRP拉索的适用范围。李翠娟等［6］利用有限元分析软件对超大跨径CFRP主缆悬索桥与超大跨径钢主缆悬索桥的静动力特性进行对比分析；齐玉军等［7］研究了FRP索和钢索的极限跨径计算；马文刚等［8］利用有限元软件对CFRP索和钢索悬索桥静力性能进行了对比研究。

以上文献，多基于有限元方法建立悬索桥模型，分析CFRP悬索桥的力学特性，基于理论方法的研究CFRP悬索桥的文献尚未见到。

中小悬索桥以索梁分析为主，大跨径悬索桥分析回归到缆索分析。Irvine［9］、Gimsing［10］、Algirdas等［11］基于公式方法研究了缆索力学特征，本文综合了以上学者的方法，对比钢索，研究了CFRP索不同跨度、不同矢跨比下的特征参数的变化规律，以及特征参数及荷载参数变化对悬索索力和位移控制方程的影响，从理论上综合分析了悬索强度、比重等材料参数，拉索跨度、矢高、截面积等几何参数，以及恒活载集度比例、作用位置等参数对大跨度缆索静力性能影响的规律，在理论上证明了CFRP悬索体系的优势和特点。

1 悬索的控制方程

1.1 悬索的平衡方程

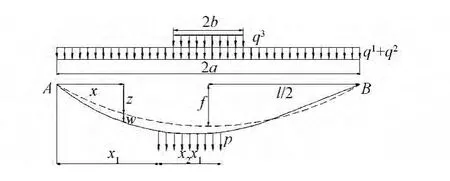
图1 受均布荷载悬索示意图

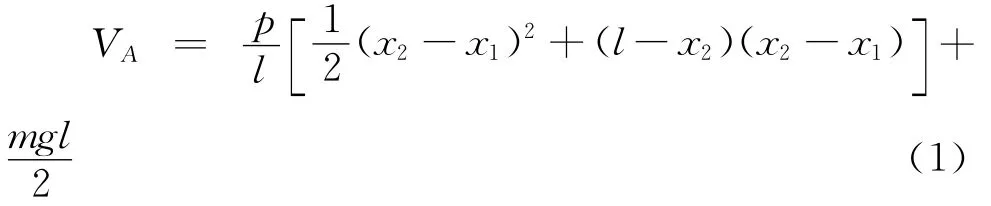
如图1所示悬索，其单位长度重量为mg、跨径为l、矢高为f。在沿跨径方向x1处施加一个荷载集度为p，长度为x2－x1的均布荷载，支座A处的支座反力VA

对于沿跨径方向任意x处，满足方程：

1.2 悬索的协调方程及索力方程

1.3 索力方程的几种特殊情形

1.3.1 满跨荷载下悬索的控制方程 式 （4）、（5）针对均布荷载任意长度的情形，即x1和x2不固定，对于荷载满布全跨，即x1＝0，x2＝1时，可以得到2个简化的方程

1.3.2 不考虑悬索弹性变形的悬索的控制方程索为柔性弹性体，在荷载作用下，其位移可分为悬索弹性伸长引起的位移和悬索几何形状改变引起的位移，对于CFRP索，有必要进一步分析弹性位移和形变位移两者的大小及其对悬索结构内力的影响。

此时，悬索的平衡方程并未发生改变，式（5）、（6）、（7）依然成立。但是此时悬索的协调方程发生变化。悬索没有弹性伸长即公式（8）中a和c的值为0，则公式（8）中的b亦为0，得式（12）。

2 悬索控制方程解的特征

由上文可知，在索力增量方程中，参数λ2和P是影响解的2个重要参数。以下将介绍λ2的意义和这2个参数对于悬索水平力相对增量h和无量纲位移w／d的影响。

图2 水平悬索示意图

2.1 参数λ2的公式及意义

如图2所示假设悬索初始状态呈抛物线状，则悬索自重沿跨径均匀分布，悬索的水平拉力分量H为：

如果悬索两端向外移动Δl／2，假设悬索不伸长，按静力平衡和变形协调条件可得到悬索内力、跨径和矢高三者变化量之间的关系：

1）按静力平衡，将式（14）对f和l分别求导可得

从以上推导可以看出，λ2是悬索的重要特征参数，反映了悬索的重力刚度和弹性刚度两者之间的比例关系，影响着悬索的刚度，是对悬索性质的重要描述参数。当λ2很小时，式（25）的分母趋近于1，ka几乎等于弹性刚度。

P和x1、x2是表示悬索的受力的无量纲参数，反映了荷载的大小和位置，是悬索水平力增量h变化的外因；λ2反映了悬索材料、截面积、线密度等自身参数以及跨度矢高等几何参数，以及悬索的初始状态，是悬索水平力增量h变化的内因，因此P、x1、x2、λ2是影响悬索特征方程解的重要参数。

2.2 悬索方程的解的特征

为了研究λ2和P对悬索静力学行为特征的影响，不失一般性，取均布荷载满布情况下的力和位移方程，即式（10）、（11），以跨中截面作为观察截面，即x＝0.5。利用计算软件Matlab计算分析参数λ2和P对悬索水平力相对增量h和无量纲位移w／d的影响。

2.2.1 参数λ2、P与悬索水平力相对增量h的关系如图3所示，分析图3可以得到：

图3 λ2、P与水平力相对增量h的关系图

1）当P一定时，在λ2较小时，随着λ2的增大悬索水平力相对增量h会有显著的增加；而当λ2增大到一定程度之后悬索水平力相对增量h趋向一个定值。这说明λ2的改变只有在其值较小时才会对悬索的内力产生影响。对于工程悬索，P一般小于10，此时当λ2≥500，其值的改变几乎不对悬索内力产生影响。

2）当λ2一定时，随着P的不断增大，悬索水平力相对增量h也增大，且P值的变化对悬索水平力相对增量h影响显著。因此，在内力控制时应注意P的取值，控制活载与恒载之间的比例尽可能小。

2.2.2 参数λ2、P对跨中无量纲位移w／d的影响 如图4所示，分析图4可以得到：

1）当P一定时，在λ2很小时，随着λ2的增大跨中无量纲位移w／d会有显著的减小；而当λ2增大到一定程度之后跨中无量纲位移w／d趋向一个定值。这说明λ2的改变只有在其值较小时才会对悬索的跨中位移产生影响，而当λ2≥400时其值的改变几乎不对悬索跨中位移产生影响。

图4 λ2、P对跨中无量纲位移w／d的影响

2）当λ2一定时，随着P的不断增大，跨中无量纲位移w／d也增大。

综上所述，当特征参数λ2较大时，即索的弹性刚度与重力刚度之比比较大时，弹性刚度在整体刚度中起主导作用时，对于特定的荷载水平，悬索的水平力相对增量h与跨中无量纲位移w／d都趋于恒定。

3 CFRP索与钢索的静力性能

根据上文的理论公式，研究大跨CFRP悬索桥的静力学特征，并与钢悬索桥进行对比分析。

3.1 两类悬索的性能参数及荷载

悬索材料的主要性能参数见表1。

表1 悬索材料的主要参数

本文算例为双向六车道公路悬索桥，悬索的荷载主要分为悬索的自重，主梁恒载和活载3部分。主梁恒载集度取定值220 k N／m。活载为公路I级荷载，不考虑集中荷载的影响，不考虑人行荷载，约取定值37 k N／m。

3.2 悬索最小截面积的确定

CFRP索和钢索在重度、弹性模量、容许应力方面存在较大的差异，为了便于CFRP索和钢索桥梁的力学行为的比较分析，需要确定CFRP索和钢索的截面面积。

考虑CFRP索和钢索的特点，根据极限设计原则，确定钢索安全系数为2.2和CFRP索的安全系数为3.0［13］，得到钢索和CFRP索的容许应力分别为818和667 MPa，矢跨比取常用值1／10，荷载布置为满跨布载。

根据公式计算得到悬索的最小截面面积。

式中：F为跨中截面内力F＝H＋H×h；σ为容许应力。

计算得到悬索的最小截面积。

表2列出了矢跨比为1／10的CFRP索和钢索在跨径从1 000～10 000 m的最小截面面积。

表2 悬索的最小截面积

从表2可以得知，虽然CFRP索的容许应力比钢索要小，但是在相同跨径相同矢跨比下CFRP索的最小截面面积要比钢索小，且随着跨径的增加两者之间的差距不断加大。这说明在等跨径同矢跨比条件下CFRP索更省材料。此外，从表2可以得知，CFRP的极限跨径明显比钢索要大，这与文献的研究结论是一致的［7］。

3.3 以特征跨度（3 000 m）为例静力性能计算

3.3.1 挠度计算位移的工况选择 如图1所示悬索，受到一个荷载长度为2a、集度为q1＋q2的恒载作用，其中q1为自重集度，q2为主梁恒载集度；同时也受到一个荷载长度为2b、集度为q3的活载作用。考虑两种工况：

工况1：活载q3正对称分布，自重q1和主梁恒载q2满布，即2a＝l。活载q3以悬索中线为对称轴正对称布置，分布长度为2b，即x1＝（a－b）／l、x2＝（a＋b）／l。

工况2：活载q3反对称分布，自重q1和主梁恒载q2满布，即2a＝l，活载q3全部布置在悬索中线的一侧（本文算例为左侧）且2b＝l／2。此种工况下即x1＝0，x2＝0.5。

在工况1情况下，Niels J.Gimsing对活载分布长度与恒载分布长度的比值即b／a，从0.1变化到1.0的过程中，考虑悬索伸长和不考虑悬索伸长两种情况下跨中竖向挠度进行了研究。结果表明b／a＝0.4时，跨中竖向挠度取得最大值［10］。由此结论，本文计算正对称荷载作用下挠度时，均全部计算b／a＝0.4时的跨中竖向挠度。即式（6）、（9）、（13）中x1＝0.3，x2＝0.7。

在工况2情况下，Algirdas等对反对称作用下的悬索的竖向挠度进行了研究，结果表明在悬索左侧四分点产生最大正挠度，右侧四分点产生最大负挠度［11］。由此结论，本文计算反对称荷载作用下竖向挠度，均全部计算在考虑悬索伸长和不考虑悬索伸长下的四分点挠度。

3.3.2 3 000 m跨径正对称均布荷载作用下的静力性能 根据表2计算结果，取CFRP索的截面面积为1.6 m2，钢索的截面面积为1.84 m2。材料性能参数同表1，矢跨比为1／10。由式（25）计算各关键截面位移及悬索内力。得到3 000 m跨径跨中截面（x＝0.5）正对称均布荷载作用下的静力性能结果如表3。

从表3可以看出是否考虑悬索的弹性伸长对内力的影响不大，但是对跨中竖向挠度影响很大，本文将就这一点在下文做详细的阐述。

3.3.3 3 000 m跨径悬索反对称均布荷载作用下的静力性能 3 000 m跨径悬索，四分点截面反对称均布荷载作用下的静力性能结果如表4。

按规范［14］要求，若出现正负挠度那么总挠度应该是正负挠度绝对值之和。由表4可知，反对称荷载产生的挠度比正对称荷载产生的挠度大。因此，反对称荷载也是一种最不利布载形式，在悬索桥设计计算中应被重点考虑。

表3 3 000 m跨径悬索受正对称均布荷载作用结果

表4 3 000 m跨径悬索受反对称均布荷载作用结果

4 跨径和矢跨比对悬索静力性能的影响

跨径是悬索桥设计计算过程中一个非常重要的参数。研究不同跨径下两类悬索的静力性能有十分重要的意义，为今后超大跨径悬索桥设计提供理论依据。本文根据两种材料不同的材料性能，分别取CFRP索跨径在1 000～10 000 m范围，钢索跨径在1 000 m至6 000 m范围。计算方法与上文所示相同，研究内容分为3部分：1）跨径变化下的参数λ2和P的变化规律；2）特殊截面的内力和挠度；3）弹性挠度和形变挠度之间比重的变化规律。计算结果如图5所示。

图5 静力性能对比

分析图5得：

1）从图5（a）得出，悬索截面面积随着跨径的增大而增大。在1 000～3 000 m范围内，特别是在2 000 m跨度以内，由于安全系数设置的差异，CFRP索截面面积和钢索截面面积差异不大；在4 000～6 000 m范围内，钢索横截面面积曲线极度陡峭，表明悬索横截面面积激增，其跨径接近了其极限跨度。由此可知CFRP索在超大跨径中更有优势。

2）图5（b）表示在一定的安全系数和矢跨比下，跨径变化对特征参数λ2的影响，进而影响了悬索控制方程解的特征。钢索和CFRP索的特征参数都会随着跨径的增加而减小。钢索的λ2的范围大致在154～172之间，CFRP索的λ2的范围大致在158～166之间。由图3和图4可知，钢索和CFRP索λ2的范围处于参数敏感区间，悬索位移增量和水平力增量对于λ2变化较为敏感，进一步分析详见第5节。

3）由图5（c）可知，对于大跨悬索，活恒载之比P远小于1。对于CFRP索，即便跨径从2 000 m增加到10 000 m，其承载比例仍然大于0.12，说明CFRP具有较高的承载能力。而钢索在4 000 m跨径以上活恒载比已经降至0.08以下，表明跨径的增加后钢悬索主要承担其自重，承担活载的能力严重不足。

4）由图5（d）和图5（e）可知，随着跨径的不断增大，悬索截面水平力的绝对增量也不断增大，且不考虑悬索的弹性伸长时的水平力的绝对增量要比考虑悬索弹性伸长时大。但只要活载相同，无论是CFRP索还是钢索水平力的绝对增量是几乎相同的。这表明截面水平力的绝对增量与活载有关，而与悬索材料无关。此外，随着跨径的增加悬索水平力相对增量在减小，然而跨径的增加会导致初始水平力H增加。综合这两种因素由图5（d）和图5（e）可知水平力的绝对增量依然是随着跨径的增加而增加的，即跨径变化时悬索水平力的相对增量与绝对增量变化不一致，也从一个侧面说明悬索初始的水平力大小十分重要。

5）图5（f）和图5（g）反映的是悬索在受到活载作用后一些特殊截面的挠度。由图可知，反对称荷载作用下跨径四分点处的挠度值要大于对称荷载下跨中挠度。在1 000 m跨径时，CFRP索和钢索在反对称荷载作用下的挠度几乎相同，但4 000 m跨径时，CFRP索的挠度增大为钢索挠度的2倍。钢索在4 000 m跨径时出现挠度曲线峰值拐点，但是CFRP索即使在10 000 m，仍未出现挠度曲线峰值拐点，但挠度增长趋势放缓。计算表明，CFRP索的最大挠度仍然满足规范要求［14］，即不大于跨径的1／250～1／300。同时由图可知，悬索的挠度实际是有两部分组成，一部分是由悬索弹性伸长造成，一部分是由悬索的形变造成，在正对称荷载情形下，弹性变形引发的跨中挠度增量绝对值较大。

6）图5（h）反应了正反对称荷载作用下，由形变引起的跨中挠度占同时由形变和弹性变形引起的跨中总挠度的比重，即刚度比重。CFRP索在正对称荷载作用下形变引发的刚度比重大致为64%，在反对称荷载作用下刚度比重大致为83%。钢索在正对称荷载作用下刚度比重大致为64%，在反对称荷载作用下刚度比重大致为83%。显然形变造成的挠度占主要部分，且在反对称荷载下刚度比重更大。但是刚度比重并不随跨径的变化发生很大改变，上下浮动不超过2%，并且钢材和CFRP在相同条件下的刚度比重值基本相同，可见，材料的差异在挠度的比例分配上不起主导作用，这一规律也揭示了大跨悬索桥的本质特征的一面。

5 悬索方程解的综合分析

上文指出λ2、P是影响悬索控制方程解的主要参数，本节将综合这两种参数分析在跨径变化过程中对控制方程（9）、（13）解的影响。

5.1 跨度对悬索索力的影响分析

图5（b）、（c）反映了跨度变化时特征参数λ2及荷载参数P的变化规律，图3反应了拉索索力增量与特征参数λ2及荷载参数P的关系。因此，将图5（b）、（c）叠放于图3并局部放大，得到图6，该图直观反映了正对称荷载作用下，跨径变化对悬索索力方程解的影响。

图6 正对称荷载对索力方程解的影响

随着跨径的变化，影响悬索索力方程的2个参数λ2和P均发生了变化。钢索的特征参数从1 000 m跨径时的171减小至5 000 m跨径时的 157；CFRP索的特征参数λ2从1 000 m跨径时的166减小至10 000 m跨径时的157。钢索的荷载参数P从1 000 m跨径时的0.14减小至5 000 m跨径时的0. 06；CFRP索的荷载参数P从1 000 m跨径时的0.16减小至10 000 m跨径时的0.11。由这些数据可以得知，两类索的这2个参数都随跨径的增加而减小，表现为向左下方的一条斜直线，说明索力增量近乎线性减少。

其中，钢索特征参数λ2和CFRP索特征参数λ2变化范围较小，两者较为接近。但荷载参数P的变化不同，CFRP变化斜线位于钢索斜线上方，且曲线长度较短，表明钢索的荷载参数P变化幅度明显大于CFRP索，这就说明在超大跨径时CFRP索承受活载的能力更强。

由于悬索索力方程参数的变化，导致两类索的水平力相对增量h也发生变化。正对称荷载情况下，钢索的水平力相对增量h从0.077减小至0. 032；CFRP索的水平力相对增量h从0.086减小至0.057。两种情况下水平力相对增量h的变化都是线性的。同矢跨比，跨径增大会使水平力相对增量h减小，但是由于两类索材料密度不同，每种情况的初始水平力H都不一样。结合图5（d）、（e）可知，水平力的绝对增量依然还是一样的，这就说明水平力的增量与悬索材料无关，与施加的活载有关

5.2 跨度对悬索变形影响分析

与图6的方法类似，将图5（b）、（c）叠放于图4中，得到图7，该图直观反映了正对称荷载作用下，跨径和矢跨比对悬索变形协调方程解即无量纲位移w／d的影响。

图7 正对称荷载对变形协调方程解的影响

跨径变化导致悬索变形协调方程参数发生变化，对方程的解，即无量纲位移w／d产生影响。正对称荷载作用下，钢索的无量纲位移w／d从1 000 m跨径时的0.015减小至5 000 m跨径时的0. 007；CFRP索的无量纲位移w／d从1 000 m跨径时的0.017减小至10 000 m跨径时的0.012。结合图10可知，两类索的无量纲位移w／d随跨径变化的变化曲线是线性的，且CFRP索的无量纲位移w／d明显大于钢索。同时，CFRP索的曲线较密，钢索的曲线较疏，说明钢索的无量纲位移w／d随跨径变化而变化的速度更快。

6 结论

1）两种主缆材料在超大跨径悬索桥的静力性能有较大差别，采用CFRP材料做超大跨径悬索桥主缆将大幅降低主缆应力中的主缆自重应力所占百分比，从而提高材料的利用率，CFRP索在超大跨径时优势更明显。

2）对于等跨径同矢跨比悬索，CFRP索的挠度明显大于钢索，但挠度依然能满足规范要求。

3）跨径变化对悬索特征参数λ2值的改变不明显，但变化范围在悬索特征参数λ2的敏感区间，对悬索水平力和位移的影响较大。

4）反对称荷载也是一种最不利布载形式，在悬索桥的设计计算过程中应被重视。

5）两类索弹性刚度占总刚度的比重基本一样，跨径对两类索弹性刚度占总刚度的比重影响很小，基本为定值。

6）两类索水平力的增量与悬索材料无关，与施加的活载有关。

［1］梅葵花，吕志涛.CFRP在超大跨悬索桥和斜拉桥中的应用前景［J］.桥梁建设，2002，（2）：75-78.

Mei K H，Lyu Z T.Application prospect of CFRP to super length suspension bridge and cable-stayed bridge［J］.Bridge Construction，2002，（2）：75-78.

［2］Meier U.Carbon fiber reinforced polymer cables：Why？Why not？What if？［J］.Arabian Journal for Science and Engineering，2012，37：399-411.

［3］吕志涛，梅葵花.国内首座CFRP索斜拉桥的研究［J］.土木工程学报，2007，40（1）：54-59.

Lyu Z T，Mei K H.First applicable of CFRP cables for a cable-stayed bridge in China ［J］.China Civil Engineering Journal，2007，40（1）：54-59.

［4］Wang X，Wu Z S.Evaluation of FRP and hybrid FRP cables for super long-span cable-stayed bridges ［J］.Composite structures，2010，92：2582-2590.

［5］Wang X，Wu Z S.Integrated high-performance thousandmetre scale cable-stayed bridge with hybrid FRP cables［J］.Composites：Part B 2010，41：166-175.

［6］李翠娟，童育强，刘明虎，等.超大跨径CFRP主缆悬索桥合理结构体系研究［J］.中国铁道科学，2011，32（1）：62-66.

Li C J，Tong Y Q，Liu M H，et al.Study on the rational structure system for super large-span suspension bridge with CFRP main cables ［J］.China Railway Science，2011，32（1）：62-66.

［7］齐玉军，冯鹏，叶列平.FRP索与钢索的求解计算和极限跨度［J］.土木建筑与环境工程，2011，33（4）：52-59.

Qi Y J，Feng P，Ye L P.Comparison of theoretical solutions and ultimate span-length between FRP cables and steel cables ［J］.Journal of Civil，Architectural ＆Environmental Engineering，2011，33（4）：52-59.

［8］马文刚，黄侨，梅葵花.大跨径CFRP缆索悬索桥的静力特性的模拟分析［J］.公路，2011（12）：98-102.

Ma W G，Huang Q，Mei K H.Model analysis of static performance for large-span suspension bridges with CFRP main cables［J］.Highway，2011（12）：98-102.

［9］Irvine H M.Cable Structures［M］.Cambridge（MA）：MIT Press，1981：59-61.

［10］Gimsing N J.Cable supported bridges concept and design［M］.John Wiley ＆ Sons，1983：90-94.

［11］Algirdas J，Arnoldas N.Displacement analysis of asymmetrically loaded cable ［J］.Journal of Civil Engineering and Management，2004：277-284.

［12］王喜军.人行悬带桥的应用及受力特性分析［D］.西安：长安大学，2006.

［13］李扬.大跨度CFRP缆索悬索桥的静力性能［J］.重庆大学学报，2012，35（8）：26-33.

Li Y.Study on static mechanics of long span suspension bridge with CFRP cable ［J］.Journal of Chongqing University，2012，35（8）：26-33.

［14］中华人民共和国行业标准.JTJ xxx-2002公路悬索桥设计规范（报批版）［S］.北京：人民交通出版社，2002.

（编辑 王秀玲）

Theoretical Analysis of Static Performance of Super Span Suspension Bridge with CFRP Cable

Wang Libin，Wu Yong
（School of Civil Engineering，Nanjing Forestry University，Nanjing 210037，P.R.China）

Equilibrium equation and compatibility equation are deduced to get the cable force equation and cable displacement control equation.Then the expression of characteristic parameterλ2in cable force equation is deduced.Meanwhile，the influence on the increment of cable force and displacement caused by λ2and load ratio P is analyzed.On this basis，taking 3 000 m span suspension bridge as a calculating example，the characteristics of the increment of cable force and cable displacement under symmetrical and asymmetrical load are studied.In this case，two different conditions are considered.One takes the elastic elongation into consideration，but the other does not.At last，compared with the steel cable，the influence on the parameter in cable force equation and displacement control equation caused by span is analyzed.The influence of the static performance of suspension bridge by parameter changing is analyzed as well.The substantive characteristics of the static performance of super span CFRP suspension bridge are cleared and the superiority and characteristics of CFRP cable structure are demonstrated in theory.

suspension bridge；CFRP cable；steel cable；static performance

U448.25

A

1674-4764（2014）02-0048-09

10.11835／j.issn.1674-4764.2014.02.008

2013-05-20

王立彬（1970-），男，博士，副教授，主要从事桥梁工程计算理论研究，（E-mail）469629649＠qq.com。