大跨悬索桥索梁锚固区疲劳养护概率优化方法

曾 勇，顾安邦，陈艾荣，谭红梅

（1.重庆交通大学a.山区桥梁与隧道工程省部共建国家重点实验室培育基地；b.山区桥梁结构与材料教育部工程研究中心 重庆 400074；2.同济大学 桥梁工程系 上海 200092）

大跨悬索桥索梁锚固区疲劳养护概率优化方法

曾 勇1a，1b，顾安邦1a，陈艾荣2，谭红梅1a

（1.重庆交通大学a.山区桥梁与隧道工程省部共建国家重点实验室培育基地；
b.山区桥梁结构与材料教育部工程研究中心 重庆 400074；2.同济大学 桥梁工程系 上海 200092）

合理的桥梁养护规划应在养护费用与失效风险之间找到一个合理的平衡。将养护费用分为检测费用，维修费用与失效费用，将线弹性断裂力学、结构可靠度理论、全寿命成本分析法结合起来，提出了基于全寿命周期成本的焊接构件疲劳养护概率优化的方法。考虑了检测概率、养护决策者的维修意愿、维修措施概率和失效概率等多种因素，把桥梁养护优化问题变为在焊接结构或构件满足在生命周期内最小允许可靠度的基础下，养护总费用最小的问题，并提出了简化计算方法。以青草背长江大桥索梁锚固区的关键疲劳细节养护为例，研究了主要参数对最优检测时刻的影响，研究结果表明，考虑了失效成本后，最优疲劳养护时刻提前，折现率对养护费用影响明显。当车辆荷载逐年增加时，索梁锚固区在设计基准期内疲劳破坏风险增大，应引起足够的重视。

线弹性断裂力学；可靠度；索梁锚固区；维修策略；疲劳；折现率；概率优化

悬索桥吊杆（索）与加劲梁之间的锚固区（通常称为索梁锚固区）是主缆和加劲梁之间的传力构件，是控制加劲梁设计的重要部位。索梁锚固区结构复杂，应力集中，吊杆（索）索力由它传给主梁，其力学性能直接关系全桥的安全［1－3］。在风与车辆等反复荷载作用下，易发生疲劳破坏。随着中国交通运输业的迅速发展，交通流量不断增加［4］，索梁锚固区更易发生疲劳破坏。

许多大跨度悬索桥修建时对吊索在钢主梁上锚固区域的疲劳性能进行了疲劳试验研究［1－3，5］。但这些研究大都集中在索梁锚固系统的受力分析与疲劳性能评估，对其养护评估涉及较少。本文基于全寿命养护方法［6］，把桥梁的养护费用分为检测费用、维修费用与失效费用，其中检测费用和维修费用为实际费用，失效费用为风险费用，将线弹性断裂力学（LEFM）、结构可靠度理论、全寿命成本分析法用于焊接钢桥的养护策略，提出了疲劳养护概率优化的方法，以辅助焊接钢桥构件养护决策；通过优化维修时间间隔实现最优的维修费用，并用于悬索桥的索梁锚固系统的疲劳维修示例中。

1 基于LEFM的疲劳寿命可靠性评估

在反复荷载作用下，钢构件会出现裂纹，且在荷载作用下不断扩展，易导致疲劳失效［7］。疲劳裂纹扩展的影响因素往往都是随机的，钢构件的疲劳寿命往往具有较大的随机性，因此其疲劳寿命可靠性评估一般采用概率分析的方法［8］。

焊接钢构件往往含有初始裂纹，疲劳裂纹形成的寿命很小，一般只需考虑其疲劳裂纹扩展寿命。疲劳裂纹扩展一般采用Paris公式［8］计算：

式中：a为裂纹尺寸；n为应力循环次数；m、C是材料的疲劳参数；ΔK为应力强度因子幅值；Δσ是应力幅值；Y（a）为应力强度的几何修正系数；Mk（a）是应力强度放大系数，反映了裂纹尖端穿过由焊趾引起的应力集中区时对应力强度因子的影响，这也是焊接构件区别于一般钢构件的修正系数［9］。

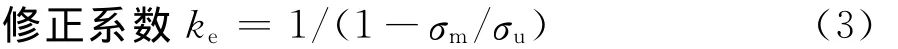
式中：σu为材料的屈服应力；σm为应力均值。

当裂纹扩展至临界失效尺寸af（超过af就会发生断裂失效或不能继续承受荷载）时，此时对应的运营年限为ts。考虑到应力循环次数的年均增长，如交

当M（t）＞0时，构件不会发生疲劳失效；当M（t）＝0时，构件处于临界状态；当M（t）＜0时，表示构件发生疲劳失效。构件的失效概率［10－11］：

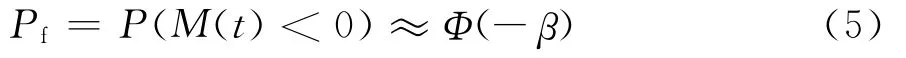
式中：Φ（·）是标准正态分布的累积分布函数；β是疲劳可靠度指标。焊接钢桥构件的疲劳寿命可靠度评估流程如图1所示。通量增加，也会导致应力循环次数增长。假设应力循环次数的年均增长率为rc，积分后，则式（1）变为：

图1 基于LEFM的疲劳寿命可靠性评估流程图

2 焊接钢桥构件的养护策略优化

2.1 裂纹检测概率

检测可发现是否裂纹存在，并测量裂纹的尺寸，检测结果决定采取何种维修措施。影响裂纹检测结果的因素多、复杂，且存在较大的不确定性。每种检测方法的检测精度q不同，相应的检测费用也不同［12］。

Pd常用的分布有指数分布、威布尔分布、对数正态分布等［13］。分布模型对最后的检测结果影响很小，一般采用指数分布来模拟ad的随机性，见式（7）。

ad是最小可检测的裂纹尺寸，当裂纹小于该值时，就不能被检测出来；λ是尺寸参数。

2.2 养护决策者的维修意愿

是否进行维修还取决于桥梁管理决策者的维修意愿，由于维修经费、维修优先级及政治考虑等因素会影响桥梁养护者的决策。参考Estes等提出的方法［14］，引入概率变量Prep来描述决策者的维修意愿概率。

其中：γΡ为影响因子，当γΡ大于1.0时，为提前维修，即预防性维修；当γΡ小于1.0时，为延迟维修，即预防性维修；当γΡ等于1.0时，为及时维修。

2.3 维修措施概率

在ti时刻进行检测裂纹后，会有3种可能的处理结果：没检测到裂纹、检测到裂纹但不维修和检测到裂纹并采取维修措施［12－13］。前2种结果不改变构件的现状，不改变结构的可靠度。检测裂纹后，根据裂纹的尺寸，采用相应的维修措施［13］。具体如下：

2.4 检测、维修概率

2.5 疲劳养护策略的概率优化

养护是减少和控制结构失效风险的一个重要的方法，但检测、维修是与费用相关的，过多的检测与维修会使养护成本增加，较少的检测与维修可能会使结构的可靠度低于目标值，增大桥梁的安全风险，使结构处于不安全状态。因此，养护应在检测、维修费用与失效风险之间找到一个合理的平衡［12］。本节把桥梁的养护总费用分为检测费用、维修费用和失效费用，其中检测与维修费用是实际发生的费用，失效费用为疲劳失效可能造成的损失，属于风险效应费用。养护总费用包括以下3种［6，12－14］：

1）检测费用Ci（q），与检测概率相关；

2）维修费用Cr（k），与维修意愿γΡ与维修措施相关；

3）失效费用Cf（ti），与检测时刻ti相关。

检测仪器越好，检测精度越高，检测费用Ci（q）越大；裂纹尺寸越大，维修费用Cr（k）越大。这些费用都是预期的，并不是现实的货币，还应考虑折现率r的影响，还需乘以其发生概率［6］。预期的检测、维修和失效费用则分别为：

桥梁疲劳检测维修优化是在给定时间ts（一般为桥梁的设计使用寿命）内，在满足结构或构件疲劳可靠度高于最小允许可靠度的条件下，预期养护总费用CT（ti，q，k）最小的问题，其优化变量为检测时刻ti、检测概率Pd、维修意愿γΡ与维修措施H（k）等。

式中：β（ti）为ti时刻的可靠度；ti∈ （0，ts］；βmin为构件的最小允许可靠度。

2.5 简化方法

如果费用变化不大，为简化分析计，忽略各检测精度与维修质量的差异，Ci（q）、Cr（k）则是常数。把检测费用Ci、维护费用Cr和失效费用Cf等效为某一中间数值C（n）的比值关系，构建各费用的百分比［12－13］。对于式（21）所示的优化问题，各变量带入后为：

3 工程应用

以重庆涪陵青草背长江大桥（以下简称青草背大桥）主梁的耳板式索梁锚固区为例，分析它在设计寿命期内的疲劳性能退化和首次疲劳检测维修的最优时刻，并进行养护分析。

3.1 工程概况

重庆涪陵青草背长江大桥位于重庆市涪陵区，主跨为788 m钢箱梁悬索桥，是重庆市也是三峡库区内最大跨径的桥梁，见图2。主桥加劲梁采用正交异性板流线型扁平钢箱梁，梁高3.5 m，宽（含风嘴）30.7 m；顶板厚14 mm，U形加劲肋厚8 mm；底板厚10 mm，其U形加劲肋厚6 mm；吊耳板厚80 mm。钢箱梁标准梁段长16 m，内设6道实体式横隔板。吊索处横隔板厚12 mm，其余横隔板厚8 mm。钢箱梁为全焊结构，作为受力的统一体，焊缝的力学性能与母材相同，钢箱梁与吊索的连接采用销接式锚板［15］。该桥的吊锚系统的构造图见图3。该桥的索梁锚固结构由连接吊索的耳板、加劲板及纵、横隔板等组成，见图4。整体的耳板下部插入钢箱梁内，吊索下端锚具和加劲钢箱梁的横隔板相连接，通过加劲板和纵、横隔板构成框式结构，起到对耳板定位、加劲和均匀板体应力的作用，并将索力传递至钢箱梁。

图2 重庆涪陵青草背长江大桥

图3 吊锚构造图

图4 索梁锚固区局部大样图

3.2 索梁锚固区的疲劳可靠度计算

初始裂纹尺寸a0为随机变量，参数C和m通常具有较大的不确定性，取为随机变量。临界裂纹尺寸口af，可根据正常使用性能的要求，根据焊接细节的尺寸来判断临界裂纹尺寸，被定义为一个确定性的尺寸参数。

Δσ的变异系数是与其获取方法相关的，一般可取0.05～0.1。本文的Δσ是利用标准疲劳车通过结构分析的方法获得的［15］。各参数的取值见表1。

表1 各参数的取值

本文只列举图1细节A的裂纹扩展及相应的维修策略。采用蒙特卡洛法求解吊杆锚固区T形焊接细节A的时变可靠度，见图5。索梁锚固区焊接细节的疲劳开裂一般不会造成桥梁结构的整体灾难性的破坏后果，但会加剧钢箱梁内部腐蚀和桥面铺装层开裂等情况的发生［8，11］。如果目标可靠度指标βmin取为2.33，对应1%的失效概率，此时对应的疲劳寿命为88 a。如果βmin取为3.03，对应0.1%的失效概率，对应的疲劳寿命为34 a。

图5 焊接细节A的可靠度指标

3.3 最优的维修时刻

从图6可以看出，当是T＝34 a时，结构的可靠度指标达到了允许的最小可靠度，此时须进行维修。这是常规的养护方法，对应于“快坏才修”的策略，结构此时已经接近破坏，失效风险很大，在此时进行维修并非最优方案。

在桥梁养护实际中，用于养护管理的费用往往是有限的。如何合理的分配用于疲劳检修中的费用是摆在养护管理部门之前的一个重要问题［14］。结合已有的研究资料［6－7，13－14］，各费用取值见表2。

表2 优化变量的取值

将数据带入式（18）～（21），得出各费用虽时间的变化。

图6显示了预期的检测，维修和失效费用之间的关系，当T＝18 a时，总费用最少，即为最优的维修时刻，比图7的34 a提前了16 a。随着运营时间的增加，结构的失效概率也逐渐增大，后期的失效成本也逐渐增大；维修概率、维修成本与运营时间成正比；失效概率与运营时间成正比。由于折现率与运营年限的影响，总成本将会出现一个最小值，此时刻为最优维修时刻。由于检测费用相对较小，影响最优维修时刻的关键影响因素是维修费用与失效费用随时间的变化。当各费用之间的相对比例关系确定以后，通过确定检测维修的时间间隔来使得化总费用最小的问题，主要还是取决于维修概率与失效概率。

图6 预期的检测、维修和失效费用之间的关系图

3.4 交通量对疲劳可靠度的影响

随着社会经济水平的不断发展，汽车保有量逐年增长，桥梁承受的交通荷载也会不断地增长，桥梁结构焊接细节所承受的疲劳荷载效应也会持续地增长。在计算服役期内焊接细节的疲劳可靠度时，须将计入疲劳荷载效应的增长。通过蒙特卡洛法模拟计算式（11），则索梁锚固区焊接细节的疲劳可靠度如图7所示。

图7 不同交通增长率下的结构可靠度指标

索梁锚固区焊接细节的疲劳开裂一般不会造成桥梁结构的整体灾难性的破坏后果，但会加剧钢箱梁内部腐蚀和桥面铺装层开裂等情况的发生［1，16］。如果采用的目标可靠度指标βmin取为2.33，对应1%的失效概率。如果采用的目标可靠度指标βmin取为3.03，对应0.1%的失效概率。从图8可以看出，当T＝87 a时，结构的可靠度指标达到了βmin＝2.00。不同的最小容许可靠度指标对焊接细节的评定也不一样。在年交通量为1%的时候，当T＝98 a时；在年交通量为2%的时候，当T＝71 a时，结构的可靠度指标达到了βmin＝2.00。交通量增长，结构的可靠度随时间下降加快，疲劳养护时间相应减短。当车辆荷载逐年增加时，索梁锚固区的焊接细节在设计基准期内就疲劳破坏风险增大，应引起足够的重视。

3.5 车辆载重变化对疲劳可靠度的影响

随着经济社会的快速发展，公路运输车辆向大型化、集装箱化方向发展，超限超载运输车辆逐年增多，对钢桥的疲劳造成严重的危害。因此，本节研究循环次数增长对疲劳可靠度的影响。车辆载重变化对应于式（4）中应力幅值Δσ的改变，应力幅均值对安全余量方程的影响很大。但限于篇幅，此次不展开论述。

4 结论

1）将养护费用分为检测费用，维修费用与失效费用，其中检测与维修费用是实际发生的费用，而失效费用属于风险效应成本，表示疲劳失效可能造成的损失。提出了钢桥焊接构件的疲劳养护优化方法，将养护优化问题变为在构件满足最小允许可靠度的总费用最小的问题。该方法考虑了平均应力、决策者的维修意愿概率和费用成本等多种因素，使分析疲劳养护优化更接近工程实际。

2）在忽略次要因素的基础上，对该疲劳养护优化方法进行了简化，该简化方法简单实用，可操作性强，适用面广。

3）以青草背大桥的主梁的耳板式索梁锚固区的疲劳养护为例，在简化次要参数的基础上分析了检测费用、维修费用、失效费用以及折现率等主要参数对最优检测时刻的影响。

4）结构的可靠度随交通量增长而下降，疲劳养护时刻相应提前。索梁锚固区的焊接细节的疲劳破坏风险随车辆荷载逐年增加而增大，应引起足够的重视。限于篇幅，本文只列举了索梁锚固区疲劳焊接一个细节的养护策略，并未列出其他疲劳细节。多疲劳细节的疲劳养护优化是今后的研究方向。

［1］陶晓燕，余振生，刘晓光，等.西堠门大桥索梁锚固部位的受力分析及模型试验［J］.中国铁道科学，2009，30（1）：49-53.

Tao X Y，Yu Z S，Liu X G，et al.Mechanical analysis and model test on the cable-girder anchorage zone of xihoumen bridge ［J］.China Railway Science，2009，30（1）：49-53.

［2］刘晓光，张玉玲.西堠门悬索桥分体式钢箱梁锚箱传力路径和疲劳性能分析［J］.钢结构，2010，25（8）：13-16.

Liu X G，Zhang Y L.Research on mechanical behavior and fatigue performance for anchor cell of separated steel box girders on xihoumen suspension bridge［J］.Steel Construction，2010，25（8）：13-16.

［3］包立新，卫星，李俊，等.钢箱梁斜拉桥索梁锚固区的抗疲劳性能试验研究［J］.工程力学，2007，24（8）：127-133.

Bao L X，Wei X，Li J，et al.Model test for fatigue performance of anchorage in cable-stayed bridge with steel box girder［J］.Engineering Mechanics，2007，24（8）：127-133.

［4］周泳涛，鲍卫刚，翟辉，等.公路钢桥疲劳设计荷载标准研究［J］.土木工程学报，2011，43（11）：79-85.

Zhou Y T，Bao W G，Zhai H，et al.Study of standard fatigue design load for steel highway bridges［J］.China Civil Engineering Journal，2011，43（11）：79-85.

［5］李小珍，蔡婧，强士中.大跨度钢箱梁斜拉桥索梁锚固结构型式的比较［J］.工程力学，2004，21（6）：84-90.

Li X Z，Cai J，Qiang S Z. Models of cable-girder anchorage for long-span cable-stayed bridges with steel box girder［J］.Engineering Mechanics，2004，21（6）：84-90.

［6］曾勇.大跨度悬索桥设计寿命期内的监测、维护与管理策略研究［D］.上海：同济大学，2009.

［7］邓扬，丁幼亮，李爱群，等.钢箱梁桥焊接细节的疲劳断裂可靠性分析［J］.工程力学，2012，29（10）：122-128.

Deng Y，Ding Y L，Li A Q，et al.Fracture fatigue reliability of welded details in bridge steel box girders［J］.Engineering Mechanics，［J］，2004，21（6）：84-90.

［8］李庆芬，胡胜海，朱世范.断裂力学及其工程应用［M］.哈尔滨：哈尔滨工程大学出版社，2008.

［9］彭洋，童乐为，Zhao Xiao-ling，等.焊接接头应力强度因子计算公式的改进［J］.工程力学，2012，29（10）：225-231.

Peng Y，Tong L W，Zhao X L，etc.Improved formulae for stress intensity factors of welded joints ［J］.Engineering Mechanics，2012，29（10）：225-231.

［10］Chryssanthopoulos M K，Righiniotis T D.Fatigue reliability of welded steel structures ［J］.Journal of Constructional Steel Research，2006，62（11）：1199-1209.

［11］吴世伟.结构可靠度分析［M］.北京：人民交通出版社，1990.

［12］曾勇，谭红梅，孙士成，等.基于概率的钢桥焊接构件疲劳养护策略优化方法［J］.中国铁道科学，2013，34（1）：29-34.

Zeng Y，Tan H M，Sun S C，et al.Probabilistic-based of optimization fatigue maintenance of weld components in steel bridges ［J］.China Railway Science，2013，34（1）：29-34.

［13］Lukic M，Cremona C.Probabilistic assessment of welded joints versus fatigue and fracture ［J］.Structure Engineering，2001，72（3）：253-264.

［14］Estes A C，Frangopol D M.Minimum expected costoriented optimal maintenance planning for deteriorating structures：applications to concrete bridge deck ［J］.Relialbity Engineering ＆System Safety，2001，73（3）：281-291.

［15］曾勇，渠昱，顾安邦.青草背长江大桥吊杆锚固系统力学性能试验研究及安全性能评估研究［R］.重庆：重庆交通大学，2012.

［16］Righiniotis T D.Effects of increasing traffic loads on the fatigue reliability of a typical welded bridge detail［J］.International Journal of Fatigue，2006，28（3）：873-880.

（编辑 胡 玲）

Fatigue Maintenance Probabilistic Optimization of Cable-girder Welded Anchorage Zones in Suspension Bridges

Zeng Yong1a，1b，Gu Anbang1a，Chen Airong2，Tan Hongmei1a
（1a.State Key Laboratory Breeding Base of Mountain Bridge and Tunnel Engineering；1b.National Engineering Research Center for Inland Waterway Regulation，Chongqing Jiaotong University，Chongqing 400074，P.R.China.2.Department of Bridge Engineering，Tongji University，Shanghai 200092，P.R.China）

it is necessary to balance the failure risk and the maintenance expensive.A methodology for reliability based maintenance optimization of steel bridge welded joints subjected to fatigue is proposed considering linear elastic fracture mechanics（LEFM），the structure reliability，life cycle cost method and maintenance strategies.The maintenance cost is divided into inspection，repair and failure sections according to the whole life cycle cost methodology.And the maintenance strategy is transformed to the minimum expected lifetime costs with a constraint of the minimum acceptable reliability index.An case concerning to a transverse stiffener of bottom flange welded joint of Qingcaobei bridge is studied with a certain number of simplifications.Some sensitivity analysis is provided.Among all the parameters，discount rate is the most remarkable.

LEFM；reliability；cable-girder welded anchorage zones；maintenance strategy；fatigue；interest rate；probabilistic optimization

U448

A

1674-4764（2014）02-0021-07

10.11835／j.issn.1674-4764.2014.02.004

2013-11-25

国家973计划前期研究专项课题（2012CB723305）；交通运输部应用基础研究项目（2013319814180）；国家留学基金资助项目（201308505149）；浙江省公路管理局科研项目（2011H41）

曾 勇（1980-），男，副教授，博士，主要从事桥梁结构分析与养护策略研究，（E-mail）zycquc＠126.com。谭红梅（通信作者），女，副教授，博士，（E-mail）hmtan2009＠126.com。