飞行器地面测控系统中天线系统时延标定*

卢华强

(中国电子科技集团公司第三十九研究所，西安 710065)

在飞行器地面测控系统中，系统测距零值标定(校零)通常是事先精确测定天线三轴中心到信标喇叭相位中心之间的距离，然后天线对准信标塔进行测距，扣除天线三轴中心到信标喇叭相位中心之间的距离后，剩余测距值即为地面系统测距零值，这个测距零值是由于天线、馈源以及上/下行信道的信号传输时延造成的，在测控任务中测得目标距离值后减去测控系统距离零值即可得到天线三轴中心到目标的真实距离值。

由于某些特殊原因，测控站无法建立满足条件的信标塔，无法采用上述方法进行测距校零，所以必须对信号经天线发射和接收时天线系统的绝对时延进行精确标定，最终计算出测控系统时延并完成对目标的高精度定位。

1 天线系统时延的划分及标定方法

地面测控系统中测站坐标系通常使用天线三轴中心作为站心坐标系原点对目标进行精确测量和定位，当系统上下行时延标定完毕后即可计算出目标距离值［1］，其原理如图1所示。假设天线三轴中心O到天线口面中心O'的距离为LOO'，测控系统测得目标T的距离为LTP，上行信号到达天线口面PP'的时延为ΔTUL，下行信号到达天线口面PP'以后的时延为ΔTDL，则天线三轴中心到目标T的真实距离D为

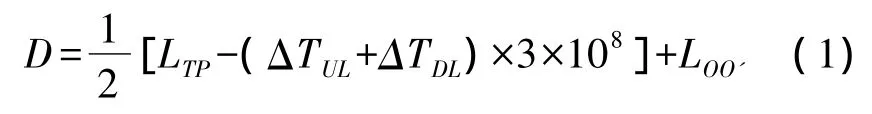
由于空间辐射的电磁波经天线放大、馈源输出后已变为封闭场的射频信号，所以上、下行信道设备的绝对时延标定较为简单，因此只介绍天线系统的时延标定方法。

图1 天线系统时延及几何示意图Fig.1 Antenna system time delay and geometry diagram

天线系统的时延Tant定义为电磁波从天线口面中心传输到馈源输出口(或从馈源输入口发射到天线口平面)所用的时间。按照电磁波不同的传输方式，可以把从天线系统时延分为天线光程时延、喇叭时延和馈源网络时延三部分，依据每部分电磁波不同的传输特点，采取相应的方法计算或测量其时延。

第一部分是如图1中喇叭相心F到天线口面P所示部分，电磁波在这一段以开放场的形式传播及反射，其传播路径符合光学原理，所需时延符合光在自由空间传播的原理，因此采用测量几何光程的方法即可计算出这一段时延［2］。

第二段是喇叭相心F到馈源网络连接法兰这一段，如图2所示，在这一段，电磁波的传播形式完成由封闭场与开放场的转换，因此对这一段时延采用计算的方法得到喇叭的传输时延。

第三段是如图2所示的网络连接法兰到馈源网络接收口或发射口这一段，包括跟踪器、极化器、双工器、滤波器等微波元件，其电磁波传播方式是封闭场形式，所以可以进行精确的测量。

图2 馈源示意图Fig.2 Feed system

1.1 天线口面到喇叭相心的时延计算

根据天线等光程反射聚焦原理，图1中电磁波到达天线口面各点后经主、副面反射到喇叭相心F的距离是相等的，即天线口面所有点到喇叭相心的光程为一常数［2］。因此，可根据设计的天线几何尺寸直接计算出时延ΔTant=ΔTAB+ΔTBC+ΔTCF。

以某工程为例，天线几何如图3所示，按照设计的天线几何尺寸可计算出波束从天线口面任意一点到喇叭相位中心的距离L为

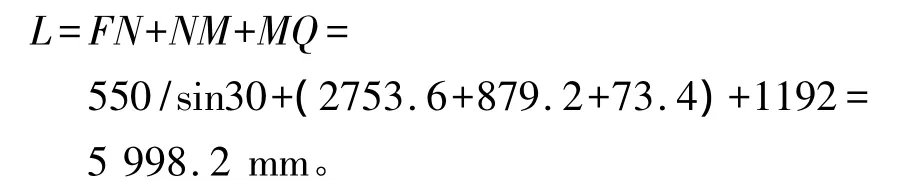
因此，计算出本段时延

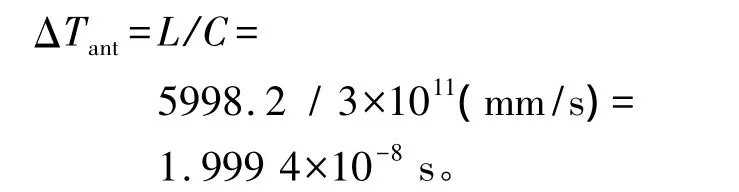
式中，C 为光速，C=3×1011mm/s。

图3 天线几何及理论光程示意图Fig.3 Antenna system geometry

1.2 喇叭相心到馈源连接法兰阶段时延的计算

喇叭相心到馈源网络连接法兰阶段的时延ΔThorn取决于波纹喇叭，波纹喇叭是由一些周期性的槽齿结构构成的，电磁波在其中传播的时延与频率、喇叭半径、槽深、齿厚、周期等各参数有关，可以根据其各个周期的特征值来计算出每个周期的时延τ，再将所有周期的时延相加就得到了喇叭的时延［3］。

单周期时延

同样以上述工程为例，按照波纹喇叭仿真设计结果及公式(2)，喇叭相心到馈源连接法兰的时延计算结果ΔThorn如表1所示。

表1 馈源喇叭时延计算结果Table 1 Calculated results of feed horn delay

1.3 馈源网络时延的测量

馈源网络连接法兰到馈源网络输入/输出口这一段时延ΔTfeed采用封闭场测试方法，测试前先要对测试附件时延标定，测试结果扣除测试附件的时延即为馈源网络的时延，示意图如图4所示。

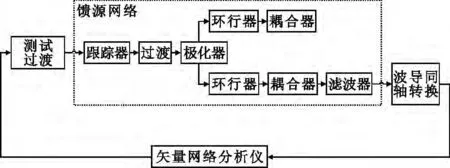
图4 馈源网络时延测量原理示意图Fig.4 Test block diagram of feed network delay

仍以该工程为例，对馈源网络时延按照图3所示的方法进行测试，为了保证测试的准确性，每一个测试频点在测试时采集多组数据并进行统计分析，其统计平均值即为最终的测试结果，而统计方差即为测试误差(时延标定不确定度)，测试结果如表2所示(测试温度15℃)。

表2 馈源网络时延ΔTfeed测试结果Table 2 Tested results of feed network

最终，可计算出该天线系统时延如表3所示。

表3 天线系统时延ΔTant计算结果Table 3 Calculated results of antenna system

2 天线系统时延标定精度分析

天线系统长时间工作于室外，阵风、伺服跟踪系统噪声及温度变化等因素都会导致天线系统时延产生变化。对这些因素进行分析可将时延变化因素分为两部分，第一部分是天线指向不准引起的时延变化，另一部分是环境温度变化导致的天线系统时延变化。

2.1 天线指向不准引起的时延变化

天线系统指向或跟踪空间飞行器时，由于指向或跟踪误差会导致天线三轴中心、天线口面中心、飞行器不在一条直线上，这就使得下行信号到达天线口面中心(或上行信号到达飞行器)时产生额外的相移ΔΦ，无论天线系统是工作于自跟踪还是指向跟踪，跟踪误差都远小于五分之一半功率波束宽度［4］，在此范围内ΔΦ由下式表示:

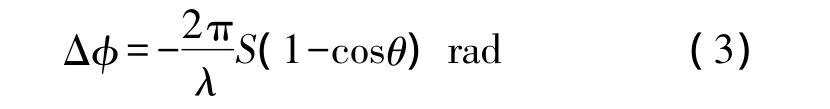
式中，λ为工作频点波长，S为三轴中心到天线口面中心的距离，θ为跟踪误差角度。

同样以上述工程为例，S为4.5183 m，假设角误差为五分之一半功率波束宽度时，其相位变化量为

因此，导致的时延标定误差为 2.82×10－4ns，可忽略不计。

2.2 环境温度引起的时延变化

外部环境导致天线系统时延变化量主要包括天线面光程变化引起的时延变化量和馈源网络温度变化引起的时延变化量两部分。天线面温差变形引起的光程时延变化相对于馈源网络温差变形引起的时延变化可忽略不计，因此只考虑馈源网络温差变形引起的时延变化，一般采用实际测量的方法标定。

仍然以某工程为例，为标定馈源网络在规定的工作温度范围内的时延变化量，将组装及测试完毕的馈源网络放入温控试验箱内，按照图4连接好测试系统，温度变化范围为－45℃～+65℃，每10℃为一个测量温度点。以－45℃的网络时延标定测试基准值，当温度达到并保持50min后，对馈源网络及测试系统的时延值进行采样，每个温度点采集40个样本数据，因此40个样本数据的统计均值即为此温度下馈源网络的时延变化量;40个样本数据的统计均方差即为馈源网络时延变化量的测量误差(时延变化不确定度)。测试所得的数据曲线如图5及图6所示。

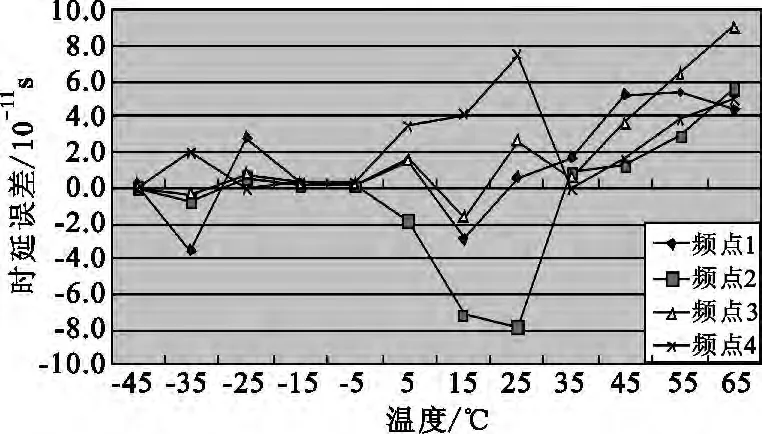
图5 各频点时延变化量均值随温度变化曲线Fig.5 The curve of mean time delay variation with temperature at each frequency point

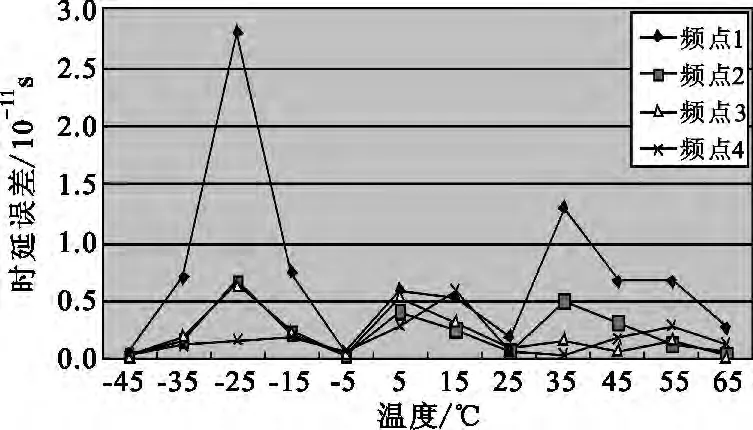
图6 各频点时延变化量均方根值随温度变化曲线Fig.6 The curve of RMS of time delay variation with temperature at each frequency point

由图5中曲线可以看出，馈源网络时延随温度增加而略有变化，并且规律性较强，在工作温度范围内频点3时延变化量最大，为0.1343 ns，只要事先标定馈源网络时延随温度的变化曲线，任务中根据馈源网络环境温度进行实时修正，即可获得很高的修正精度。

由图6中数据曲线可以看出，馈源网络在不同点频、不同温度测试的时延数据一致性较好，最大测量误差出现在频点1、－25℃时约为0.028 ns，其原因为馈源网络在该点频驻波较大所致。

3 结论

通过以上分析计算及某工程多台套天线的工程实践验证，可得出以下结论:

(1)采用分段测量、计算天线系统时延的方法，其结果可作为飞行器地面测控系统中天线系统时延修正的依据;

(2)因天线跟踪/指向误差引起的系统时延变化可忽略不计;

(3)当天线系统时延标定误差要求较高时，需事先标定馈源在规定温度范围内的时延变化，任务中实时测量馈源网络环境温度，根据曲线对时延进行修正，可保证天线系统时延标定精度优于0.1 ns。

［1］刘嘉兴.飞行器测控通信工程［M］.北京:国防工业出版社，2010.LIU Jia－xing.Aircraft TT＆C Communication Engineering［M］. Beijing:National Defence Industry Press，2010.(in Chinese)

［2］周朝栋，王元坤，杨思耀.天线与电波［M］.西安:西安电子科技大学出版社，1994.ZHOU Chao－dong，WANG Yuan－kun，YANG Si－yao.Antenna and Radio Wave［M］.Xi'an:Xidian University Press，1994.(in Chinese)

［3］Jasik.Antenna engineering handbook［M］.New York:McGraw Hill，1961:1－1021.

［4］Best S R.Positioning Error Associated with Antenna Phase－Center Displacement in Time－Reference Radio Distance－measurement.Steven R［J］.IEEE Antennas and Propagation Magazine，2004，46(2):13－22.