基于耦合灰色关联度TOPSIS法的缓倾斜薄矿脉采矿方法确定

曹 帅，王成刚，张永林，盛学栋，崔志勇，赵继勇

（1．北京科技大学 土木与环境工程学院，北京100083；2．山东黄金矿业（莱西）有限公司，山东 莱西266616）

缓倾斜薄金矿脉在我国地下黄金开采中占有较大比重。而类似赋存条件的金矿品位往往较高，诸如大尹格庄1号矿脉、夏甸金矿等，如何实现安全高效开采就显得意义重大。多年来，这类矿体的采矿方法一直困扰着许多矿山，主要因为这类矿体的开采难度极大，采矿方法选取不当极有可能导致矿石贫化严重，影响矿山的经济效益。正确确定采矿方案是矿山企业设计和生产中必须解决的重要问题，是矿床开采成败的核心［1］。就目前而言，采矿方法选择主要采用经验类比法和盈利分析法，而经实践证明，这样的分析方法普遍存在较大的片面性和主观性，科学性不强。近年来，随着统计分析法、模糊数学法［2－4］及灰色关联度等数值决策方法的不断发展，其应用已由原先经济、化学及生物等领域逐渐扩展到土建、地质及采矿等工程领域。曹帅［2］和徐文彬［3］等利用层次分析法对两种不同赋存条件的矿体采矿方法进行了优选；谭玉叶［4］等利用模糊聚类和层次分析法优选了武钢程潮铁矿的采矿方法；申艳梅［5］等利用模糊聚类分析法进行了围岩支护技术的综合评判；韩现民［6］、朱国辉［7］应用模糊数学进行了采矿方法及矿柱回采优选的研究工作。国内其他学者就模糊数学也做了大量的研究工作［8－10］，虽取得一定成效，但仍存在不足。主要表现在指标权重确定的研究方法比较单一，增大了分析问题的主观性，降低了分析结果的可靠性。本文以山东黄金矿业莱西山后矿区金矿为研究背景，结合TOPSIS法（逼近理想解法）和灰色关联度理论的优势，最终确定出适合开采缓倾斜薄矿脉的理想采矿方案。

1 灰色关联度TOPSIS法模型构建

1．1 TOPSIS法

TOPSIS是 Technique for Order Preference by Similarity to Ideal Solution的简称。TOPSIS法又称逼近理想解法，通过构造多指标问题的理想解和负理想解，并以靠近理想解和远离负理想解两个基准作为评价各对象的判断依据。由于该方法使用灵活简便，被广泛应用于企业筹资、投资决策、物流管理及环境评价等领域［11－13］。其计算过程如下：

1）设有m个目标（有限个目标），n个属性，专家对其中第i个目标的第j个属性的评估值为xij，得初始判断矩阵V ＝ （vij）m×n。

2）由于构成初始矩阵中的各个指标量纲可能不同，需要对初始矩阵进行归一化处理，然后得到标准矩阵Y ＝ （yij）m×n。其中：

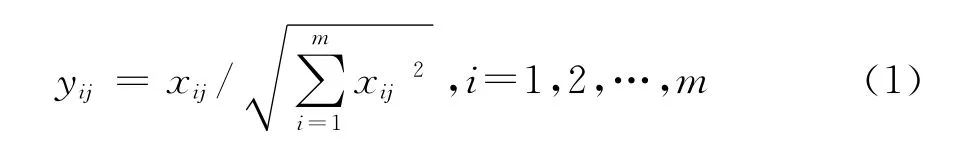
式中，yij为标准矩阵元素，xij为第i个目标的第j个属性的评估值。

3）根据DELPHI法获取专家群体对指标属性的信息权重矩阵B，所构成得到的综合加权判断矩阵为Z＝YB ＝ （yijωj）m×n。

4）确定正理想解和负理想解

正、负理想解：

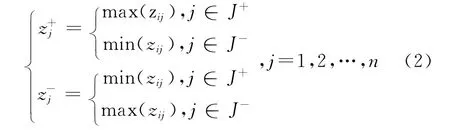
式中，J＋为效益型指标，即越大越优的指标集合；J－为成本型指标，即越小越优的指标集合。

5）正负理想解欧氏距离计算

正、负理想解欧氏距离：

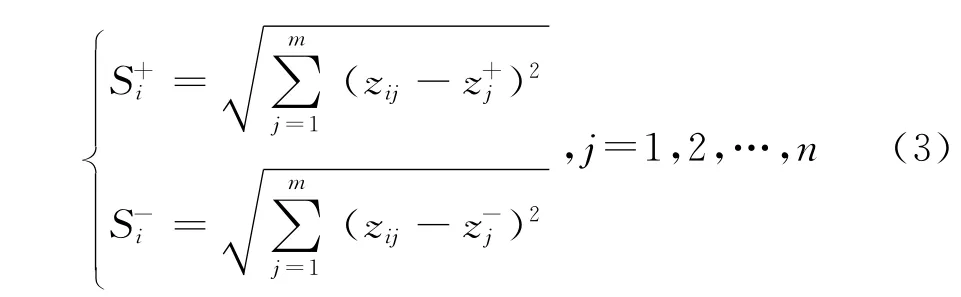
式中，Si＋为正理想解欧氏距离，Si－为负理想解欧氏距离。

6）方案集相对贴近度计算

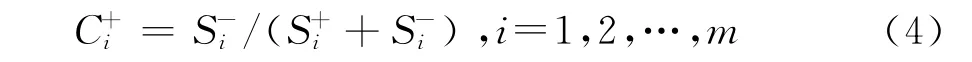
式中，Ci＋为相对贴近度。

7）依据相近贴近度值的大小对方案进行排序，相对贴近度越大则对应方案越优。

1．2 灰色关联度法

灰色关联度是一种多因素统计分析方法，是以各因素的样本数据为依据用灰色关联度来描述因素间关系的强弱、大小和次序的，若样本数据列反映出两因素变化的态势基本一致，则两者之间的关联度较大，反之，关联度较小［14］。相比传统的相关、回归等多因素分析方法，灰色关联度对数据要求较低且计算量较小，因此该方法已被应用于社会及自然等各个科学领域。其计算过程如下：

1）确定最优指标集

设Y 为多目标决策域集合，Y＝｛Y1，Y2，…，Ym｝，Yi为待选采矿方案名称，同时设X为指标要素集合X＝｛X1，X2，…，Xm｝，Xi为函数对应指标。设定指标因素的权向量 W ＝｛W1，W2，…，Wm｝，且满足Wi＞0，且权值和为1。根据指标因素相对优化原则，选取各指标的相对最佳值，构成正理想指标集；同时选取各指标因素的相对最差值作为负理想指标集。

2）指标归一化

鉴于各经济技术评判指标间通常具有不同量纲，因此不能直接进行比较，为保证结果可靠性，需要对原始指标进行归一化处理。设第k个指标的变化区间为［jk1，jk2］，则可以用下式将上式中的原始数值变成无量纲值Cik。

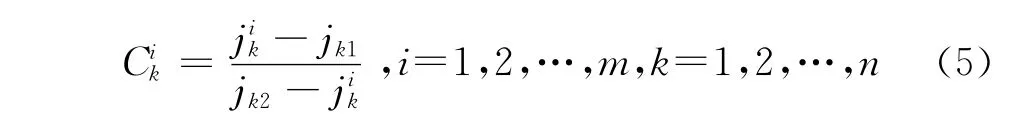
其中，Cik为指标归一化后无量纲值，jk1为第k个指标在所有被评价对象中的最小值，jk2为第k个指标在所有被评价对象中的最大值。

3）关联系数及灰色关联度计算。

正、负理想方案关联系数：

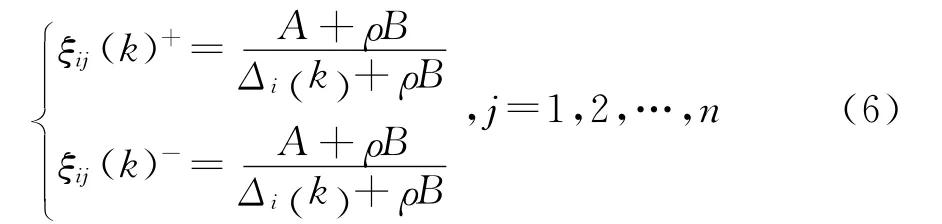
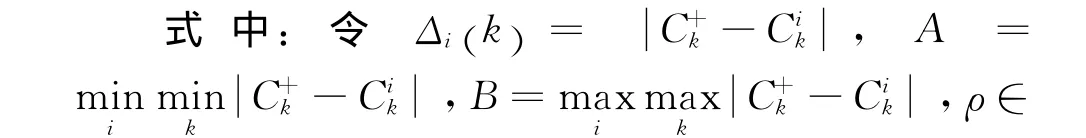
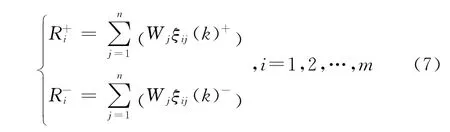
式中，Ri＋为正理想方案的灰色关联度，Ri－为负理想方案的灰色关联度，Wj为权向量指标，ξij（k）＋和ξij（k）－分别对应正、负理想解方案的关联系数。

4）依据正理想方案关联度大小进行排序。

1．3 耦合灰色关联度TOPSIS法模型构建

TOPSIS法能充分利用原始数据的信息，反映各方案之间的差距，客观真实地反映实际情况，具有真实、直观、可靠的优点。但是该方法在反映方案数据曲线之间态势变化或形状相似性方面存在一定的缺陷。而灰色关联度又正好可以反映方案数据曲线之间的态势变化［15］。鉴于此，将上述两者结合起来构建一种新的评价尺度能更确切地描述待评测样本与理想样本之间的贴近程度，并以此对样本优劣进行排序，提供样本决策依据。利用此方法进行的决策方案计算步骤如下：

1）指标权重确定。在指标权重确定过程中，为较为客观地反映决策指标的重要性，仅仅使用主观赋权值确定实际指标权重主观性较差，不能反映实际指标的真实情况。因此决定采用主观赋权值和熵值法对决策指标进行组合赋权，具体组合赋权公式为：

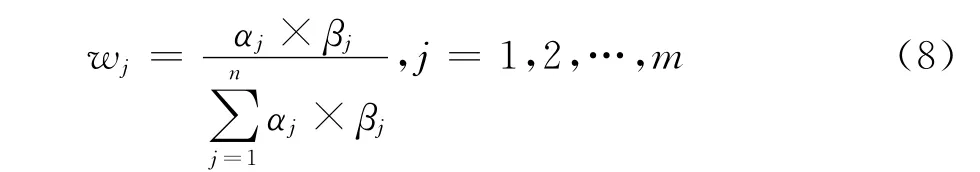
式中：αj和βj分别为利用主观赋权法和熵值法确定的第j个指标的权重，wj为第j个指标的组合权重值。

2）决策矩阵向量归一化进行标准化处理。

3）计算加权标准化判断矩阵V。

4）确定正理想解Z0＋和负理想解Z0－。

5）计算方案正理想解和负理想解之间的距离Si＋和Si－及灰色关联度Ri＋和Ri－，并进行无量纲化处理，计算公式为：

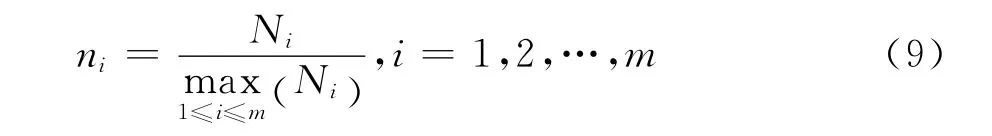
式中：Ni分别代表Si＋、Si－、Ri＋、Ri－。

6）合并无量纲化欧氏距离和关联度，合并公式可确定为：

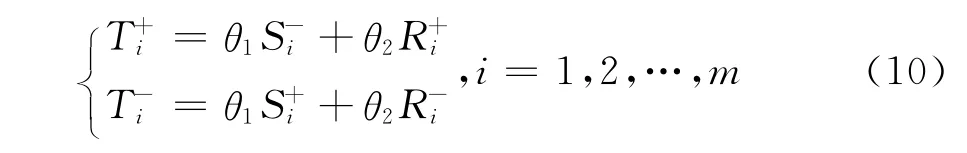
式中：Ti＋和Ti－分别表示样本与正负理想解的接近程度；θ1和θ2反映的是决策者对相对位置和形状的偏好程度，且满足θ1＋θ2＝1。

7）计算相对贴近度。新的贴近度结合了欧氏距离和灰色关联度，更准确地反映待评样本与正负理想解在态势变化上的接近程度，相对贴近度公式为：

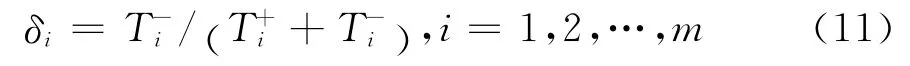
式中，δi为新的相对贴近度。

8）相对贴近度排序。根据上述计算所得相对贴近度值并对其进行排序，贴近度值越大，反映其与正理想解越接近，方案越优。

2 实证分析

2．1 工程背景

山后矿区金矿体均产于招平主断裂带以下1号矿脉内，矿体围岩主要岩性为黄铁绢英岩、黄铁绢英岩化碎裂岩，与围岩无明显边界，呈渐变过渡状态。矿区内部共圈定金矿体7个，其中1－2号矿体规模较大，为矿床内主要矿体，1－3号矿体次之。各矿体特征如下：1－2号矿体：分布于16～26勘探线间，＋156～－477m标高范围内。矿体形态简单，呈板柱状产出于主裂面下盘20m范围内。走向NE30°～33°，倾向SE，倾角38°～46°，矿体走向长平均257m。矿体平均厚度3．99m，金平均品位3．29 g／t。1－3号矿体：分布于16～24线，赋存标高＋130～－644m。矿体呈板柱状且主要赋存于1－2矿体下部，矿体走向NE32°，倾向SE，平均倾角40°。矿体走向平均长181m，矿体平均厚度1．95m，金平均品位2．58g／t。其它矿体规模较小，水文地质条件较为简单。

2．2 采矿方法经济技术评价指标确定

根据山后矿区金矿的开采技术条件，结合国内外开采类似赋存条件矿体的采矿方法，选定分段空场嗣后充填采矿法（1）、上向进路充填采矿法（2）、上向水平分层充填采矿法（3）组成初始待选方案集。采矿方法选择除了适应矿床地质赋存条件确保生产安全以外，应尽可能地提高经济效益和社会效益。因此选择采矿方法必须考虑很多指标和因素，而这些指标和因素的影响程度有大有小，为了能准确表现出其影响程度，须对其进行加权计算。在此考虑的因素有以下两类：定量指标，采矿成本A、采切比B、损失率C和贫化率D和生产能力E；定性指标，采矿工效F、安全程度G、通风条件H、生产管理熟悉程度I、劳动强度J和对矿体变化的适应程度K等，具体评判经济技术指标见表1。

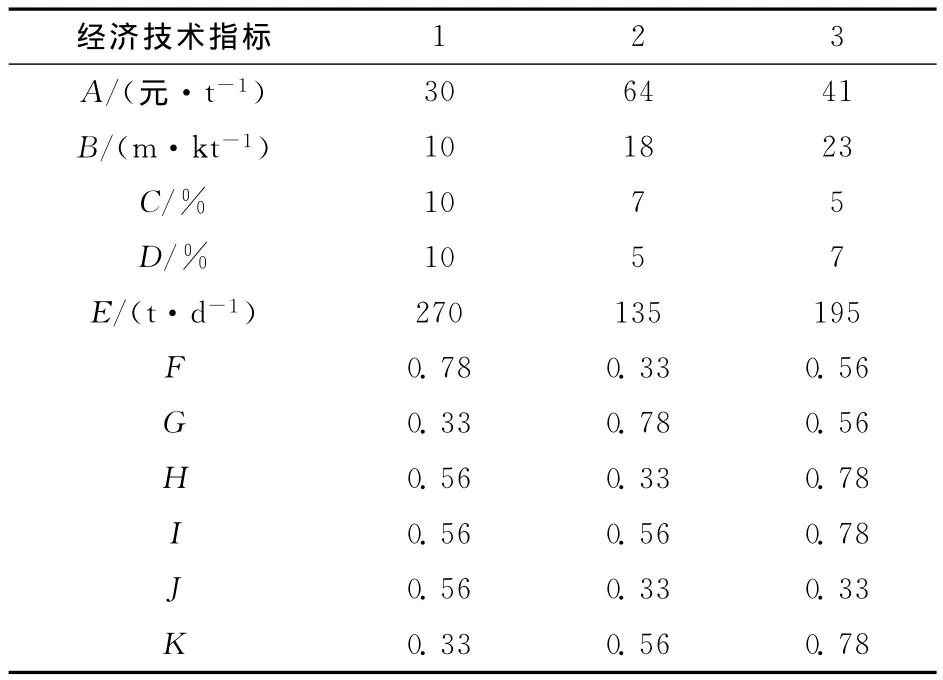
表1 待选采矿方案经济技术指标Table 1 Economic and technical indexes of mining project

2．3 耦合灰色关联度TOPSIS法采矿方案决策

1）指标权重确定

利用极差法对数据进行标准化，通过计算信息熵值确定数据中第i项的权系数得到βi，根据公式（8）计算得到组合权重列 向 量 为W＝ （0．092，0．072，0．084，0．084，0．073，0．077，0．076，0．076，0．142，0．143，0．076）。观察数据发现，以往矿山生产主要关注的诸如采矿成本、采切比、贫化率、损失率及生产能力等定量指标占有比例为41%，而定性指标生产管理熟悉程度和劳动强度两项指标值均达到14%以上，定性指标综合占有比例接近60%，可知，定性指标的评判在今后指导矿山生产时应引起足够的重视。因此，应用组合权重确定评价指标权重比较合理。

2）决策矩阵标准化

利用向量归一化对决策矩阵进行处理后得到标准化矩阵，见表2所示。

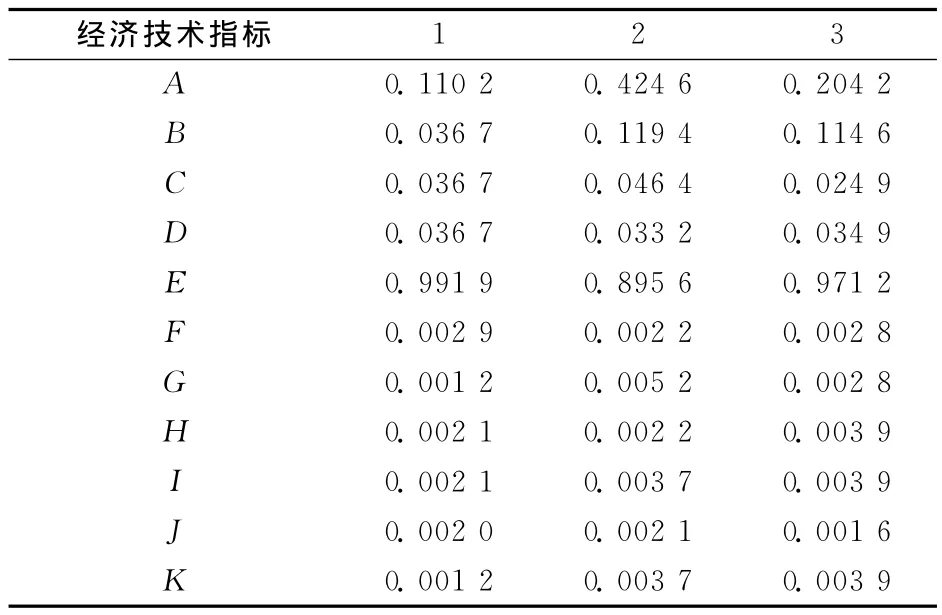
表2 各经济技术指标标准化矩阵Table 2 Standardized matrix of economic and technical indexes

3）计算加权标准化判断矩阵

结合上述计算得到的组合权系数矩阵和向量归一化后得到的矩阵，根据公式（1）和（5）计算得到标准化判断矩阵见表3所示。

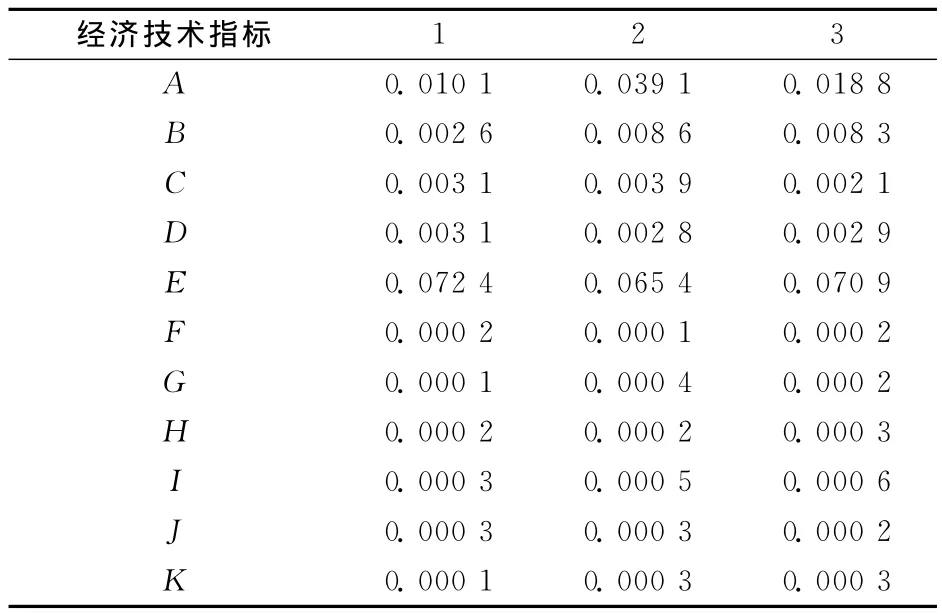
表3 各经济技术指标标准化判断矩阵Table 3 Standardized judgment matrix of economic and technical indexes

4）确定正理想解Z0＋和负理想解Z0－

根据公式（2）、（6）和（7）计算得到的正理想解和负理想解结果见表4。

5）无量纲化处理后的欧氏距离Si＋和Si－及灰色关联度Ri＋和Ri－。

根据4）计算得到的正理想解和负理想解，利用公示（3）、（6）、（7）和（9），计算得到无量纲化处理后的欧氏距离和灰色关联度见表5。

6）无量纲化距离和关联度合并

按照合并公式（10），这里取θ1＝θ2＝1／2，Ti＋和Ti－分别表示样本与正负理想解的接近程度，最终得到：Ti＋＝ （0．603 8，1，0．683 2），Ti－＝ （1，0．610 6，0．799 6）。

表4 经济技术指标正、负理想解Table 4 Positive and negative ideal solution of economic and technical indexes

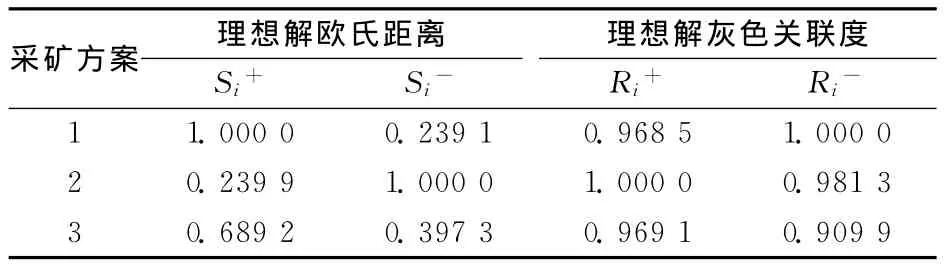
表5 各经济技术指标的欧氏距离和灰色关联度Table 5 Euclidean distance and grey correlation grade of economic and technical indexes

7）相对贴近度计算和排序

根据公式（11）带入计算方案的相对贴近度为δi＝（0．376 5，0．620 9，0．460 8），由贴近度最大原则可以得到，方案2的相对贴近度为三者之中最大的，达到了62．09%，方案3次之，方案1则为本次采矿方案中最差的。

2．4 相对贴近度对比验证分析

计算得出的耦合相对贴近度结果满意程度有必要进一步对比验证，对TOPSIS法和灰色关联度法计算出的采矿方案贴近度进行对比研究，三种方案贴近度指标见表6。

为直观反映三种决策方案的相对贴近度情况，由Origin软件做出采矿方案编号与相对贴近度值的关系曲线，见图1。

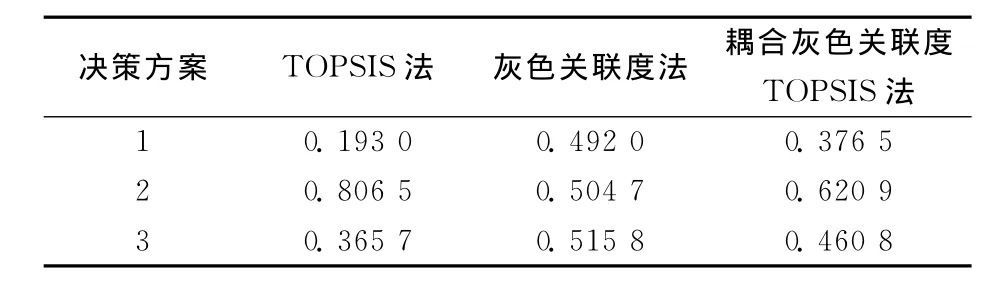
表6 决策方案相对贴近度指标Table 6 Relative closeness indexes of decision scheme

观察发现采用TOPSIS法决策方案，上向进路充填法的贴近度系数达到80．65%，远高于分段嗣后充填法的19．30%和上向分层充填法的36．57%，具有绝对优势；灰色关联度决策方案计算得到的贴近度系数十分接近，最大偏差控制在5%范围内，并未起到真正意义上的决策作用，效果不理想；而利用耦合灰色关联度TOPSIS法得到的相对贴近度曲线介于TOPSIS法和灰色关联度法之间，能够较为合理的从三种采矿方案中优选较为符合山后矿区金矿的采矿方案，更具有合理性和科学性。

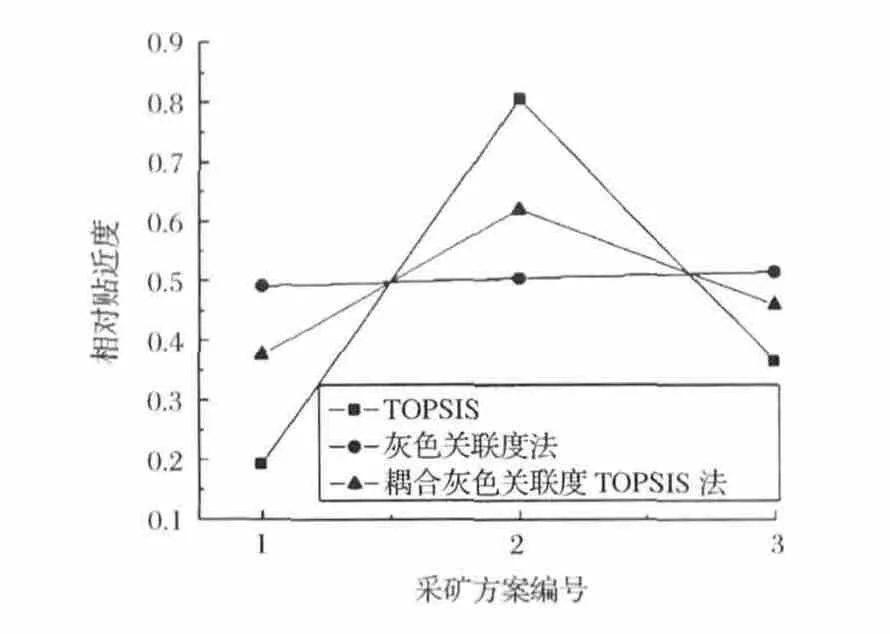
图1 采矿方案编号与相对贴近度关系Fig．1 Relationship between mining scheme number and relative closeness

3 结论

1）基于几种常规开采缓倾斜薄矿脉的采矿方法，综合考虑影响采矿方法优选的11个因素指标，采用主观赋权值和熵值法对决策权重进行组合赋权计算，较好地克服了单纯使用主观赋权法造成的不客观。

2）结合TOPSIS法和灰色关联度法的各自优势，建立耦合灰色关联度TOPSIS法综合评判模型，得出分段嗣后充填采矿法、上向进路充填采矿法和上向水平分层充填采矿法相对贴近度依次为37．65%、62．09%和46．08%。确定了上向进路充填采矿法为适合山后矿区金矿的最优采矿方案，并与TOPSIS法和灰色关联度法得出的贴近度结果进行对比验证，吻合程度较好，更具合理性和科学性。

3）山后矿区金矿属新建矿山，更兼由于平行矿脉上盘招—平大断裂带断层泥的存在，加大了实际采矿难度，更对矿体安全高效开采提出了巨大挑战。因此，在确定上向进路充填采矿法为主体采矿方案的同时，应考虑引进上向水平分层充填采矿法进行平行矿脉联合回采，合理确定两者使用比例将作为下一步研究工作的重点。

［1］ 李 明，郑怀昌，赵 勇，等．多目标决策密切值法在侯庄矿采矿方法优选中的应用［J］．矿冶工程，2010，30（1）：5－8．

［2］ 曹 帅，宋卫东，朱先洪，等．高海拔地区急倾斜薄矿体采矿方法优选［J］．金属矿山，2013（2）：14－17．

［3］ 徐文彬，宋卫东，杜建华，等．缓倾斜极薄铁矿体采矿方法选择研究［J］．金属矿山，2011（4）：5－8．

［4］ 谭玉叶，宋卫东，雷远坤，等．基于模糊聚类及层次分析法的采矿方法综合评判优选［J］．北京科技大学学报，2012，34（5）：489－494．

［5］ 申艳梅，韦四江．回采巷道锚杆支护效果模糊综合评判［J］．采矿与安全工程学报，2011，28（4）：576－580．

［6］ 韩现民，李 晓，杜国栋．模糊评判在露天转地下矿山的矿房结构参数优化中的应用［J］．工程地质学报，2006，14（5）：654－660．

［7］ 朱国辉，胡平安．基于模糊综合评判法的矿柱回采方案优选［J］．湖南有色金属，2009，25（1）：1－3．

［8］ 王新民，赵 彬，张钦礼．基于层次分析和模糊数学的采矿方法选择［J］．中南大学学报，2008，39（5）：875－880．

［9］ 王元汉，李卧东，李启光，等．岩爆预测的模糊数学综合评判方法［J］．岩石力学与工程学报，1998，17（5）：493－501．

［10］ 王建国，杨林章，单艳红．模糊数学在土壤质量评价中的应用研究［J］．土壤学报，2001，38（2）：176－183．

［11］ 李 刚，迟国泰，程砚秋．基于熵权TOPSIS的人的全面发展评价模型及实证［J］．系统工程学报，2011，26（3）：400－407．

［12］ 胡永宏．对TOPSIS法用于综合评价的改进［J］．数学的实践与认识，2002，32（4）：572－575．

［13］ 李晓峰，刘宗鑫，彭清娥 ．TOPSIS模型的改进算法及其在河流健康评价中的应用［J］．四川大学学报，2011，43（2）：14－21．

［14］ 李圣梅．灰色关联度分析法在企业业绩评价中的应用［J］．价值工程，2007（4）：40－42．

［15］ 张毅娜．基于TOPSIS优选法和灰色关联度法的房地产项目投资决策研究［D］．西安：西安建筑科技大学，2008．