金佛山水库取水口岩质高边坡动力稳定性分析

王俊杰，吴 洋，刘良军

(1. 重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；2. 重庆交通大学 水利水运工程教育部重点实验室，重庆 400074；3.重庆市水利电力建筑勘测设计研究院，重庆 400020)

我国地处世界两大地震带交汇地区，地震活动频繁，地震诱发的边坡滑移、崩坍破坏十分常见[1]，尤其是复杂的岩质高陡边坡，受岩体结构类型及原岩应力等因素影响，岩体受力变形及动力响应十分复杂[2-3]，其动力稳定性分析及灾害机理研究已成为当前岩土工程领域亟需解决的难点问题。目前，边坡动力稳定性分析方法主要有拟静力法、有限滑动位移法、安全系数时程分析法、动力有限元法等，但由于岩体结构及其本构关系复杂，以及地震载荷的不确定性[4-5]，使得地震作用下的边坡变形破坏机理及岩体动力响应规律的研究成果较少[6-7]，有必要进行进一步的探讨。

笔者基于重庆金佛山水库坝址取水口岩质高边坡工程实例，采用荷兰岩土工程有限元软件Plaxis，基于动力有限元时程分析法，结合拟静力法及工程地质分析，综合评价了边坡加固前后在地震作用下应力变形及稳定性状况，对类似岩质高边坡工程具有较强的参考借鉴意义。

1 工程概况

1.1 地形地貌

重庆市南川区金佛山大2型水利工程坝址区属四川盆地南东边缘与云贵高原北端交汇地带，具有明显成层性特征，属深切中山地貌。坝址所在柏枝溪河谷，右岸取水口边坡地形较左岸平缓，边坡大部为基岩裸露，岩层除缺失泥盆系外，寒武系至白垩系地层均有出露，地层岩性为碎屑岩(砂岩、泥岩)与碳酸盐岩(灰岩、白云岩)相间分布。右岸取水口岩质高边坡顶部为S2h页岩，边坡主体为S1x粉砂岩夹少量页岩，其下为一层S1X泥质条带灰岩，高程750 m以下河床主要为S1L页岩。由于在取水口边坡修建取水隧洞、取水塔的需要，坡顶按63°开挖，下部依5级阶梯面开挖。设计加固方案采用挂网锚喷混凝土支护加固，C 20喷射混凝土厚度100 mm，上部水泥砂浆锚杆长3.2 m，下部水泥砂浆锚杆长5 m。取水口岩质高边坡剖面见图1。

图1 取水口岩质高边坡剖面(单位：m)

1.2 地震评价

金佛山水库工程区地质构造属南北径向构造体系的川黔南北构造带的一部分——新洲隆褶带的中心，受基底主要断裂破碎带影响，周边地震活动对工程所在区域影响较小。取水口岩质高边坡地震地质评价工作区属于华南地震区的西侧部分，近代构造及地震活动性较弱，主要为频度不高的中等强度地震，6级和6级以上地震极少。1854年12月24日南川县陈家场附近发生的5.5级地震，震中距坝址约24 km，是距离坝区最近、对坝区影响最大的历史地震。依据GB 18306—2001《中国地震动参数区划图》，工程区地震动动峰值加速度参数为 0.05 g，地震反应谱特征周期为0.35 s，对应的地震烈度为Ⅵ度。

2 计算原理

Plaxis动力分析理论建立在线弹性基础之上[8]，动力荷载作用下，物体运动的基本方程为：

(1)

式(1)的最后两项与静态变形相符，在质量矩阵M中考虑材料质量，由总矩阵实现。

时间积分采用Newmark隐式积分法，任意时刻质点位移与速度在t+Δt时分别表示为：

(2)

(3)

式中：Δt为时间步；α及β为控制积分精度的控制参数，与瑞利阻尼αR及βR并非同一概念，笔者采用α=0.25，β= 0.5的组合参数。

在执行中，通过隐式时间积分，在最终时间步(t+Δt)结束时可得：

(4)

3 计算模型及材料参数

3.1 计算模型与边界条件

有限元模型(以加固后边坡为例)采用15节点三角形单元，基于三角剖分原理，优化生成非结构性的网格，并对临空面及前缘部分网格进行局部细化(图2)，应变单元1 077个，节点总数8 863个。在开挖加固后1，3，5级临空阶梯面外侧设置A，B，C等3个监测点(图1)，以水平向右为x轴正向，垂直向上为y轴正向，各监测点坐标见表1。

表1 地震监测点坐标

模型底部设置为固定约束边界，通过指定位移(ux=0.01 m，uy=0.00 m)实现地震荷载的施加。为防止地震应力波反射，左右两侧采用黏性吸波边界吸收辐射波，通过阻尼器代替固定约束。

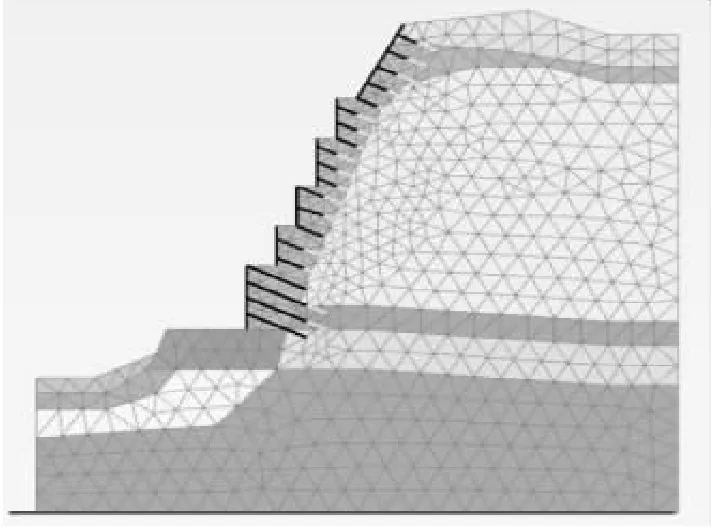
图2 模型单元网格Fig.2 Grid of FEM model

3.2 材料参数

锚喷支护中厚度10 cm的混凝土面板采用具有较大的抗弯刚度和轴向刚度的板单元模拟，设为线弹性模型，轴向刚度为3×106kN/m，抗弯刚度为2 500 kN/m，泊松比为0.2。预应力锚杆锚固段及自由段分别采用土工格栅及点对点锚索模拟，取锚杆锚固段轴向刚度为2×107kN/m，自由段轴向刚度为2×105kN/m，锚杆预应力为200 kN，通过在分布施工步骤里中输入预应力来实现。

边坡岩土体材料参数由室内试验确定，见表2。

表2 岩土材料参数

3.3 输入地震波

输入地震波采用USGS记录的1989年美国Upland地区真实地震波加速度数据，数据以SMC格式记录，样本率200 Hz，震中距5 km。依据SL 203—97《水利抗震设计规范》，金佛山水库取水口岩质高边坡在场地基本烈度Ⅵ度基础上提高1度作为设计烈度，即按照地震烈度Ⅶ度进行抗震设防，因此将原始地震波加速度峰值调整至0.1g(100 cm/s2)，并进行漂移修正，输入地震波加速度时程曲线见图3。

图3 地震波加速度时程曲线Fig.3 Seismic acceleration-time corve

4 边坡动力响应分析

4.1 锚喷加固对边坡动力响应影响

图4为地震作用下锚喷加固前后边坡塑性应变云图。塑性应变集中带通常是边坡最易发生变形破坏的部位，对比可见，加固后边坡易滑区域塑性应变明显减小，特别是坡顶后缘塑性应变集中区域已不明显，锚杆深入岩体内部产生轴向锚固力，能显著提高区域岩体抗滑性能，有效地抑制了地震作用下边坡裂隙的形成和发展。

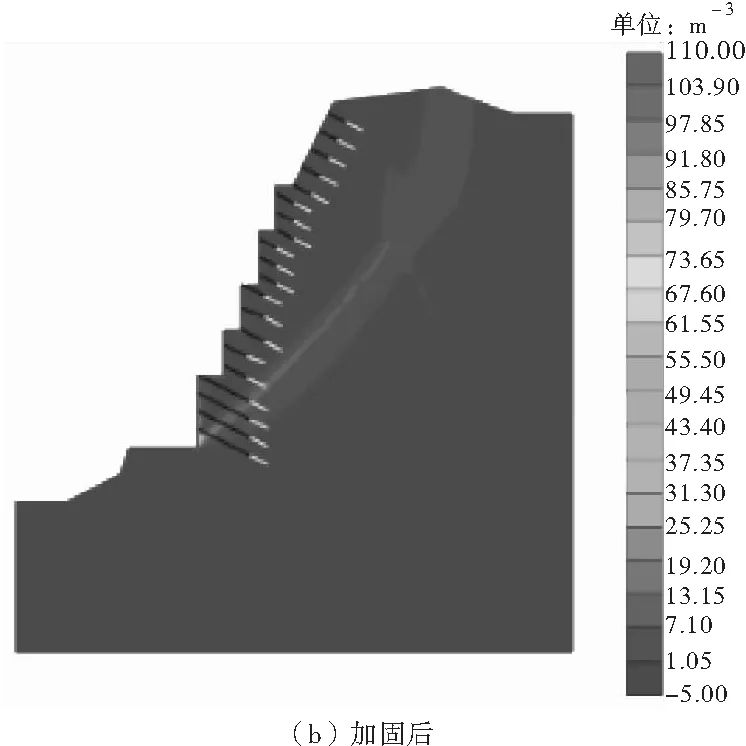
图4 锚喷加固前后边坡塑性应变云图Fig.4 Nephogram of slope plastic strain before and after shotctete reinforcement

图5为加固前后监测点C水平位移时程曲线。可以看出锚喷支护加固对于岩体位移起着明显的控制作用，加固后监测点C震后永久位移仅为15.3 mm，较开挖时减小63%。结合拟静力法计算结果，加固后边坡抗震安全系数为1.72，较开挖时提高约7%，说明该设计加固方案行之有效，能够有效减小边坡后发型滑移破坏可能性。

图5 锚喷加固前后监测点C水平位移时程曲线Fig.5 Horizontal displacement-sime curves of point C before and after shotcrete reinforcement

4.2 加固后边坡动力响应规律

4.2.1 位移时程规律

图6为监测点位移时程曲线。可以看出地震作用下边坡岩体产生位移波动，各监测点波动变化趋势基本一致，其质点位移主要以水平方向为主，竖直方向只存在微小位移，与水平位移相比基本可以忽略。在地震扰动影响下，监测点分别在2.4 s和5 s附近发生最大负向位移和正向位移，位移响应峰值为正向23.8 mm，负向26.9 mm，此时局部岩体可能发生应力超限，但由于地震加速度作用时间极短，并且地震作用下岩体最大位移也较小，并非意味此时边坡最易失稳破坏。随着地震波动逐渐平缓，岩体水平位移由正向转为负向，并最终趋于恒定值。

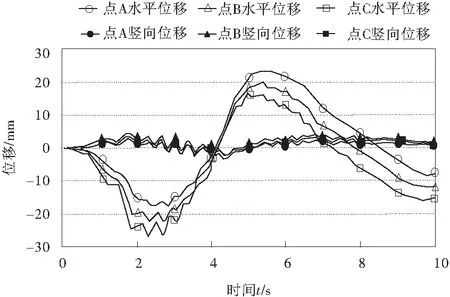
图6 监测点位移时程曲线Fig.6 Displacement-time curves of monitoring points

4.2.2 地震作用后边坡应力场

了解边坡岩体动应力分布特性，对于分析地震作用下边坡破坏机制是十分必要的。

图7为地震作用后边坡应力场分布云图。可以看出地震作用引起了边坡应力重分布，震后边坡应力分布以压应力为主，并未出现明显的拉应力集中区。最大主应力δ1与静力作用下应力分布规律相似，从边坡临空面向基岩深部逐渐递增，最小主应力δ3愈近于坡面愈趋于0。岩体结构对岩质边坡地震动力响应起着关键的控制作用，左岸边坡底部为S1x泥质条带灰岩和S1L页岩软弱结构面，由于岩体分布的不连续不均匀，使得岩层分界面附近出现明显的应力阻滞现象，坡脚处应力显著增高，坡脚应力集中带下凹面朝向边坡临空方向，推测潜在滑坡为自上而下的压致拉裂式破坏模式。

图7 地震作用下边坡应力场Fig.7 Slope stress field in the earthquake

4.2.3 加速度、速度响应规律

一般认为在边坡较低的情况下，地震加速度随边坡高程增加具有“垂直放大现象”[9]或呈现出“较强的线性规律”[10-11]，但金佛山水库左岸岩质高边坡坡顶到坡脚接近150 m，且开挖加固后边坡坡顶呈63°斜坡，下部为5级阶梯状临空面，局部凸起地形对有限区域动力系数起明显的放大作用，但边坡整体范围内地震加速度放大系数时而增大时而减小，不再随高程而线性放大，呈现不规则分布，其中监测点A加速度放大系数为1.25，监测点B放大系数为1.17，监测点C放大系数为1.45。

图8为边坡监测点水平速度时程曲线。可以看出岩体运动速度随地震波动显著，全程监测点水平方向速度远大于竖向速度，岩体振动以水平方向为主。受地震累积效应影响，地震发生后4 s左右，岩体质点水平方向速度达到峰值，滞后于地震波普变化。

图8 监测点水平及竖向速度时程曲线Fig.8 Horizontal and vertical velocity-time curve of monitoring points

4.3 加固后边坡动力稳定性评价

断裂破碎带附近，尤其是岩体构造作用复杂、岩体松散破碎或风化严重的地区，地震作用所导致的边坡变形破坏是不可忽视的。

图9为地震作用下边坡位移矢量图及剪应力云图。可看出易滑岩体主要集中在边坡前缘，坡脚及岩层分界面处发生剪应力集中，地震作用下边坡岩体由静态系统突变为动态系统，地震惯性力及循环波动震荡导致边坡强度降低，当岩体抗剪强度或抗拉强度小于地震惯性力所产生的剪切力、扭转力或拉应力时，边坡局部将发生剪切或拉伸破坏，岩体出现细微裂隙并不断扩大而逐渐形成上下贯通的破坏面，边坡可能沿此破坏面发生惯性失稳。

图9 边坡位移增量矢量及剪应力云图Fig.9 Incremental displacements vector and shear stress nephogram

但是由于取水口岩质高边坡所属工程区属于华南地震区西侧的金佛山-綦江地震带，具备控制6级左右地震的背景，对工程场区影响烈度达到Ⅵ度的几率很小。并且金佛山水利工程工程建设场地处于扬子准地台之上扬子台褶带内，区域差异性运动较弱，各级地貌形态清晰且保存完整，坝址区附近主要断裂带近期无明显活动迹象，动力计算结果显示各监测点位移响应峰值不超过27 mm，震后永久位移均在16 mm以内，结合拟静力法计算所得边坡安全系数，开挖后边坡抗震安全系数为1.61，加固后边坡抗震安全系数为1.72，均满足工程规范要求，因此可认为坝坝址区地质构造稳定，取水口岩质高边坡抗震性能较好。

5 结 论

1)采用Plaxis有限元软件，采用人工修正的加速度时程作为地震输入条件，针对锚喷支护加固前后重庆金佛山水库左岸岩质高边坡进行动力稳定性分析，获得了边坡应力变形及岩体质点动力响应规律，可为实际工程设计及施工提供可靠的参考依据。

2)锚喷支护抗震效果显著，有效地抑制了地震作用下边坡裂隙的形成和发展，约束了地震作用下的边坡变形，加固后边坡动力稳定性明显提高，发生后发型滑移破坏的可能性降低。

3)地震作用下边坡岩体运动方向主要以水平方向为主，局部岩体可能发生应力超限，边坡底部S1x泥质条带灰岩和S1L页岩岩层分界面附近应力阻滞现象显著，震后边坡应力分布以压应力为主，并未出现明显的拉应力集中区。

4)金佛山左岸岩质高边坡高度接近150 m，临空开挖面为不规则的阶梯状，局部动力响应放大作用显著，因此边坡整体范围内地震加速度放大系数为不规则分布，不再随高程变化而呈现线性规律。受地震累积效应影响，边坡岩体质点速度响应滞后于地震波普变化。

5)受软弱结构面控制，地震作用下边坡可能发生自上而下的压致拉裂式滑移破坏，但由于金佛山水库坝址地区域构造稳定性较好，强震频率较低，按地震烈度Ⅶ度进行工程抗震设防时边坡整体安全，大规模惯性滑移失稳可能性较小。

[1] 王风昊.复杂岩质边坡的动力稳定性和加固效应研究[D].南京:河海大学,2007.

Wang Fenghao.Study on Dynamic Stability and Stabilization Effect of Complicated Rock Slopes [D].Nanjing: Hohai University, 2007.

[2] Al-Homoud A S,Tahtamoni W W. Reliability analysis of three- dimensional dynamic slope stability and earthquake-induced permanent displacement[J].Soil Dynamics and Earthquake Engineering,2000, 19(2):91-114.

[3] Lin J S,Whitman R V.Earthquake induced displacements of sliding blocks [J].Journal of Geotechnical Engineering,1986,112(1):44-59.

[4] Kumsar H,Aydan O,Ulusay R.Dynamic and static stability assessment of rock slopes against wedge failures [J].Rock Mechanics and Rock Engineering, 2000, 33(1): 31-51.

[5] Kovacevic M S,Jasarevic I,Kulic Z.Plane equilibrium of rock slopes with anchors[C]//Proceeding of the International Symposium on Assessment and Prevention of Failure Phenomena in Rock Engineering. Istanbul,Turkey: A.A. Balkema,1993: 653-660.

[6] Wang Junjie.Hydraulic Fracturing in Earth-Rock Fill Dam [M].Beijing:China WaterPower Press,2012.

[7] 史石荣,陈林杰,余超.基于强度折减法的高烈地震区边坡稳定性分析[J].重庆交通大学学报:自然科学版,2011,30(2):273-276.

Shi Shirong,Chen Linjie,Yu Chao.Slop stability analysis in high-intensity earthquake zone by strength reduction method [J].Chongqing Jiaotong University: Natural Science, 2011, 30(2): 273-276.

[8] 北京金土木软件技术有限公司.PLAXIS岩土工程软件使用指南[M].北京:人民交通出版社,2010.

Beijing Civil King Software Technology Co.Ltd..Geotechnical Software User Guide of PLAXIS [M].Beijing: China Communications Press, 2010.

[9] 王存玉,王思敬.岩体工程地质力学问题(七):边坡模型振动试验研究[M].北京:科学出版社,1987.

Wang Cunyu,Wang Sijing.Issues of Rock Mass Engineering Geomechanics(VII): Model of Slope Vibration Test Research [M].Beijing: Science Press,1987.

[10] 何蕴龙,陆述远.岩石边坡地震作用近似计算方法[J].岩土工程学报,1998,20(2):66-68.

He Yunlong,Lu Shuyuan.A method for calculating the seismic action in rock slope[J].Chinese Journal of Geotechnical Engineering,1998, 20 (2): 66-68.

[11] 祁生文.岩质边坡动力反应分析[M].北京:科学出版社,2007.

Qi Shengwen.Rock Slope Dynamic Response Analysis [M].Beijing: Science Press, 2007.